基于多机制优化螺旋飞行特征的乌燕鸥算法

李光泉, 刘欣宇, 王龙飞, 邵鹏

(江西农业大学计算机与信息工程学院, 南昌 330045)

近些年来,各国学者们由于深受自然界动植物的特征行为而倍受启发,并通过模拟自然界生物的各种觅食行为、攻击行为和繁殖行为等提出了一系列的群体智能优化算法。群智能优化算法种类众多,但因为其结构简单、易于扩充且效果显著而深受广泛学习研究。例如:鲸鱼优化算法[1](whale optimization algorithm, WOA)、粒子群算法[2](particle swarm optimization, PSO)、樽海鞘群体算法[3](salp swarm algorithm, SSA)、蝴蝶优化算法[4](butterfly optimization algorithm, BOA)、灰狼优化算法[5](grey wolf optimization, GWO)、海鸥优化算法[6](seagull optimization algorithm, SOA)、乌燕鸥优化算法[7](sooty tern optimization algorithm, STOA)等。其中,乌燕鸥算法就是近年来一种新兴的群智能优化算法,其主要是通过特殊的迁徙行为和攻击行为,实现了算法在全局搜索和局部搜索的主要功能,并因为算法的可操作性强,可实现性高,目前在一些工业问题和分类问题上均取得了良好效果。然而,也因为算法有限的搜索能力和单一的搜索方式,导致了算法较易陷入局部最优,并随着迭代次数的增加会导致种群多样性的不断减小,降低了算法在搜索后期的收敛速度及收敛精度。

为此,针对STOA存在的不足,中外学者们倾向于从算法混合、单策略优化、多策略优化以及基于实际工程问题优化等多角度提出广泛的改进方法,并在不同的函数集和实际问题上进行仿真实验。贾鹤鸣等[8]通过将遗传算法和乌燕鸥算法进行混合,并通过平均适应度值进行评估,以此加强乌燕鸥算法的局部搜索能力,证明了该算法在数据挖掘领域具有广阔的工程应用前景;肖永江等[9]通过将遗传算法的变异思想融入乌燕鸥算法中,提出了一种新颖的改进乌燕鸥算法并进行了DG的优化配置,大大提高了算法收敛速度和精度;乔夏君等[10]针对传统PID参数整定存在的问题,通过引入混沌映射提出了一种混沌乌燕鸥算法(chaos sooty tern optimization algorithm, CSTOA)用以优化发动机参数自整定PID控制;Soni等[11]通过引入乌燕鸥算法对动态经济排放调度问题进行了优化和解决。同时,孙珂琪等[12]提出一种混合正余弦算法和Lévy飞行的自适应乌燕鸥算法,并将其应用于解决桥式起重机主梁结构优化设计中;雒珊等[13]为解决算法局部最优能力和寻优能力较低的问题,提出了一种混合Lévy飞行和热交换混沌乌燕鸥算法,并将算法应用于二级斜齿圆柱齿轮传动机构可靠性轻量化设计,实现了齿轮传动机构轻量化设计的目的;而李家帅等[14]针对行星齿轮箱振动信号的非线性特征明显、故障特征难以识别的问题,提出了一种基于乌燕鸥算法的故障诊断方法用以提取磨损故障特征频率;李月英[15]和王国柱等[16]则在此基础上提出了一种改进的乌燕鸥算法和多策略改进的乌燕鸥算法,有效地解决了移动机器人在复杂环境中的最优路径规划问题和桥式起重机主梁质量减重问题。

上述研究不仅在一定程度上平衡、增强了乌燕鸥算法在全局寻优和局部寻优的能力,而且对于算法的收敛速度及收敛精度也有了本质的提升。然而,由于SOTA自身独特的寻优方式,导致算法仍然存在着“全局强,局部弱”的显著优缺点。为了能在更大程度上提高算法的局部搜索能力和收敛速度,现提出一种融合混沌映射、自适应惯性权重与高斯变异的多机制乌燕鸥优化算法(GT-STOA)。首先,通过采用Tent混沌映射对种群进行初始化;其次,引入自适应惯性权重优化机制,增强算法的局部搜索能力,并在此基础上引入高斯变异机制,此为提升算法跳出局部极值的能力。由此可见,基于多机制协同优化的GT-STOA不仅增强了种群的多样性,而且提升了算法在全局搜索和局部搜索的能力,从而使之具备更强的寻优能力和算法鲁棒性。

1 乌燕鸥优化算法

1.1 乌燕鸥迁徙行为

(1)避免碰撞:为了防止乌燕鸥群体间产生相互碰撞,附加变量SA将会用于计算新的搜索代理位置,以避免相邻乌燕鸥个体之间的碰撞,并计算产生乌燕鸥的新位置:

(1)

(2)

z=0,1,…,Maxiterations

(3)

式中:Cf为一个线性调整SA的控制变量,它的值从Cf线性减小至0;z为当前迭代次数;Maxiterations为最大迭代次数。

(2)聚集:乌燕鸥个体在迁徙过程中避免相互碰撞后,群体之间会朝着最佳个体所在的位置方向进行移动。

(4)

CB=0.5Rand

(5)

(3)更新:最终,乌燕鸥可以根据最佳个体所在的位置方向更新其轨迹和最终位置。

(6)

1.2 乌燕鸥攻击行为

攻击行为是乌燕鸥种群重要的特征行为之一,在迁徙的途中,它们可以依靠自身重量和羽翼改变它们的速度、高度和攻击角度等。当乌燕鸥群体攻击猎物时,它们便会在空中产生特定的螺旋行为。具体表现形式如下。

x′=Rsini

(7)

y′=Rcosi

(8)

z′=Ri

(9)

R=uekv

(10)

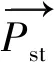
(11)

2 乌燕鸥算法的优化设计

2.1 混沌初始化机制

乌燕鸥种群的初始位置对于乌燕鸥最优位置的移动搜索会存在较大的影响和一定的约束,在STOA算法中就初始位置的更新方式而言主要是通过在搜索空间中随机生成位置序列而产生的。随机初始化所得的确定位置,虽然在一定程度上保证了初始位置的随机性,但是就种群的多样性而言同样带来了极大的不确定性,也无法保证个体位置的均匀分布,从而导致种群多样性和寻优速度的降低。

通过学者们的不断尝试和复现,并结合混沌映射的遍历性特征和随机性特征,王贺琦等[17]将Tent映射用于了优化改进人工蜂群算法,毛清华等[18]则融合改进Tent混沌方法优化了灰狼算法等。以此为鉴,本文研究将引入Tent混沌映射机制优化乌燕鸥种群初始化过程,具体映射函数表达式为

(12)

式(12)中:t为映射次数,t=0,1,2…;xt为第t次所得的映射函数值;γ为混沌参数,在本文中设为定值2。

假设在二维搜索空间中,设定种群数量为200,将随机种群初始化后的位置分布同引入混沌映射后的种群初始化位置分布图进行直观比对。由图1(a)可以发现,随机初始化种群所得的遍历位置分布散乱,随机性较大。反观图1(b),在引入Tent映射优化初始种群位置后所呈现出的分布趋势是较为均匀的,由此直观地反映出Tent映射初始化种群具有一定的优化效果。

图1 种群初始化位置分布示意图

2.2 自适应惯性权重优化机制

乌燕鸥优化算法中的惯性权值是衡量算法收敛速度和寻优结果的一个重要指标。当惯性权重取值较大时,算法会因为大权值的存在而表现出显著的全局搜索能力,而当惯性权重取值较小时,算法则更会表现出卓越的局部搜索能力。由此,归于乌燕鸥算法的迭代过程。因为变量SA在寻优过程中充当着惯性权重的重要作用,所以本文研究将针对变量SA进行自适应权重优化。通过迭代次数的递增适当地对权值进行自适应缩小,用以增强算法的局部搜索能力,平衡算法在全局搜索和局部搜索的性能。综上,具体的优化模型如下。

(13)

(14)

2.3 高斯变异优化机制

乌燕鸥优化算法由于小步长搜索特性的存在而表现出了显著的全局搜索能力而被广泛应用于实际问题的优化解决中,但同时也是因为减小了搜索步长给算法的局部搜索带来了一定的负影响。不仅如此,在STOA的迭代执行过程中,种群内乌燕鸥位置的多样性会伴随着迭代次数的不断递增而大幅下降,由此削弱了算法精细搜索的能力,使得算法过早的陷入局部最优,降低了算法寻优性能。

鉴于此,所受李文超等[19]将高斯变异算子作为自花授粉更新公式,叶坤涛等[20]通过高斯变异扰动更新种群蜘蛛最优位置为启发,并综于乌燕鸥算法的小步长搜索机理,本文研究在乌燕鸥种群完成迁徙攻击搜索后针对种群内的最优个体位置Posbest通过高斯变异机制执行优化更新,具体机制模型为

Posbest=Posbest[0.1+kGaussian(0,1)]

(15)

式(15)中:Posbest为乌燕鸥的最优个体位置;k为在区间[0,1]中的随机数;Gaussian(0,1)为服从均值为0、方差为1的高斯分布。

2.4 GT-STOA算法流程及描述

GT-STOA算法是一种由多机制优化后的群智能算法,其本质是通过模拟乌燕鸥种群的迁徙行为和攻击行为进行数学模型复现,以达到定位搜索和快速寻优的效果。

针对传统乌燕鸥算法存在的不足,通过融合混沌映射,自适应惯性权重和高斯变异扰动展开了多机制辅助优化。主要包括在种群初始化位置的更新,惯性变量权值的自适应性扰动以及在最优个体位置的更新上进行针对性优化,帮助算法丰富了种群多样性,提升了收敛速率和提高了寻优精度等。综上所述,GT-STOA算法的整体执行过程如下。

步骤1初始化乌燕鸥种群{xi|i=1,2,…,N},初始化参数SA、CB和Maxiterations,并由式(12)混沌映射函数更新种群初始化位置。

步骤2计算乌燕鸥个体的适应度值Pst(x),寻找适应度值最优所属乌燕鸥的所处位置Pbst(x),记录此时最优解Xbest。

步骤3由式(13)和式(14)计算自适应权重值,通过自适应权重的结果更新乌燕鸥个体的位置。

步骤4由式(1)、式(4)、式(6)计算乌燕鸥个体的运行轨迹和最终位置。

步骤5由式(7)～式(11)计算乌燕鸥最终的螺旋飞行位置Pst(x+1)。

步骤6更新计算目标函数适应度值,保留最优乌燕鸥个体位置。

步骤7由式(15)通过高斯变异对最优乌燕鸥个体位置进行扰动更新,选择保留两者中适应度值更好的解,并更新最优解Xbest。

步骤8判断结束条件,如果已满足结束条件,则准备结束程序,输出所得结果,否则跳转步骤2。

步骤9程序执行结束,输出最优位置及最优解Xbest。

GT-STOA的算法伪代码如下。

GT-STOA伪代码Begin初始化参数,种群规模N,测试函数F,最大迭代次数Maxiterations;按式(12)Tent初始化种群,计算个体适应度值,寻找种群最优位置Pbst(x);While t < Maxiterations do for i = 1 to N do 按式(13)和式(14)计算自适应权重值,并由此更新种群个体的位置; end for for i = 1 to N do 按式(15)对最优个体位置进行扰动更新; end forend WhileEnd

2.5 时间复杂度分析

算法的时间复杂度对评判算法的性能有着至关重要的作用。为此,计算STOA算法在优化后的时间复杂度。

当对于种群大小为N、维度为D的启发式算法 STOA而言,其所得的时间复杂度为O(ND)。而对于多机制优化后的GT-STOA而言:Tent映射初始化参数所需时间的为ND,自适应惯性权重优化个体位置所需的时间为ND,高斯变异扰动最优个体位置所需的时间也为ND。综上,GT-STOA整体的时间花费为

ND+ND+ND=3ND

(16)

由此可见,本文GT-STOA算法的时间复杂度为O(3ND),通过对照算法STOA的时间复杂度O(ND)发现二者的时间复杂度并没有显著性差异,故本文的多策略优化并不会对算法效率造成负面影响。

3 实验仿真与结果分析

3.1 实验环境及参数设置

本次实验的测试环境为64 位 Windows 10 操作系统,实验软件由MATLAB R2018b负责执行算法运算。

同时,为了充分证明GT-STOA算法的可行性和准确性,也为保证算法执行结果的相对公平性,在本文的仿真实验中将统一算法的测试方法与测试数据。其中,种群数量设定为30,最大迭代次数为500,并且为了防止算法执行过程的随机性影响,所有实验均独立运行30次,记录实验结果的平均值、最优值和标准差。

3.2 测试函数

为了验证GT-STOA的优化效果,选用12个基于不同特征的基准测试函数进行仿真实验。其中,F1～F7是单峰测试函数,F8～F11是多峰测试函数,F12则是固定维度的多峰测试函数,测试函数的具体信息如下:F1为Sphere函数, F2为Schwefel 2.22函数, F3为Schwefel 1.2函数, F4为Schwefel 2.21函数, F5为Rosenbrock函数, F6为Quartic函数,F7为Sum Squares函数,F8为Rastrigin函数,F9为Ackley函数,F10为Griewank函数,F11为Alpine函数,F12为Foxholes函数。

3.3 仿真结果分析

为验证GT-STOA算法的寻优性能,选取PSO作为经典智能优化算法的代表。同时,为了衡量GT-STOA在新型领域及相关研究领域的寻优效果,选取多策略海鸥优化算法[21](multi-mechanism seagull optimization algorithm, GEN-SOA)、非洲野狗算法[22](design optimization algorithm, DOA)、CSTOA、GWO、SSA、BOA、SOA和STOA 9种对照算法进行对比实验。

从实验直观性角度出发,将GT-STOA同所有对照算法一起,取F1～F12测试函数的最优值,平均值和标准差如表1中统计所示。同时,根据各算法的寻优结果将绘制部分测试函数的收敛曲线图用于收敛性分析,如图2所示。

表1 10种不同算法的实验对比

图2 对比算法收敛图

3.3.1 算法精度分析

针对实验的单峰测试函数F1～F4而言,GT-STOA和GEN-SOA均在算法执行结果中找到了理论最优值,并且GT-STOA相对于其他对照算法而言也实现了精度数值最优的结果,并在F7、F8、F10和F12函数也都寻及理论最优值。对于单峰测试函数F5,SOA与GEN-SOA算法在最终的寻优结果的精度上取得了较好的效果,而STOA则相对来说寻优效果较弱。对于测试函数F6,GT-STOA通过自适应惯性权重的优化表现出了最优的寻优结果,而CSTOA则仅次于此,在数值精度上平均高出近2个数量级左右。然而对于多峰测试函数F8～F11,就F8可以发现,GT-STOA与5个算法同样在函数值上找到了理论最优值。对于F9而言,GT-STOA与GEN-SOA和DOA所能寻及的最优值相同,但同样是所有对照算法中的最优,并且得益于算法的多机制辅助优化,帮助它们所得的标准差均为0,提升了算法在寻优过程的稳定性,而GWO,BOA等则紧随其后。对于测试函数F10,在最终结果上GT-STOA、GEN-SOA、GWO、DOA和CSTOA均找到了理论最优值,并且GT-STOA、GEN-SOA和DOA在平均值和算法稳定性指标上的表现也十分出色。针对测试函数F11中GT-STOA与GEN-SOA在结果中找到了理论最优。而在F12函数中,虽然SSA表现出了较全面的寻优能力,但总体而言,GT-STOA的寻优能力依旧出色。

3.3.2 算法收敛性分析

结合收敛图2和表1可以发现,针对测试函数F1～F12而言,GT-STOA、GEN-SOA和DOA 3种算法的全局最优值均以相对较高的速率进行收敛下降,并且算法在全局勘测和局部寻优的协调能力中有着显著的优越性,实例表现在测试函数F5和F6等在后期依旧能够通过有力的局部搜索找到最优值。其中,对于测试函数F1、F3和F10,GT-STOA均在250以内便收敛到了全局最优值,并且表现出了收敛速度最快,收敛精度最小的显著效果。而在测试函数F8和F10中所表现出的收敛性最强,在50代后便收敛到了算法最优值也是全局最优值。展现了GT-STOA算法稳定且显著的全局寻优能力。

3.4 高维函数的实验分析

综合上述各算法的精度分析及收敛性分析发现,GT-STOA在低维度寻优过程中有着显著性效果。基于此,为充分验证算法在高维度条件下所显现的寻优能力,对6个测试函数在100维情况下进行仿真实验,比较GT-STOA与各类代表性算法在高维情况下的寻优能力。算法的实验参数与3.1节一致,实验结果如表2所示。

表2 高维函数对比

由表2的实验结果可知,当测试函数的维度提升至100维时,GT-STOA针对不同类型的单峰函数和多峰函数依旧能在不同的对照算法中表现出更优的寻优能力。在测试函数F2、F4、F10和F11中GT-STOA也找到了函数的理论最优值,并且对于实验结果的均值和标准差而言,也展现出了算法在高维情况下显著的稳定性。由上述分析可知,GT-STOA在处理高维优化问题方面也具有一定的竞争优势。

3.5 非参数统计检验

为避免上述所得的算法结果会出现片面性且无法进行统一定性分析等问题,同时为了更好地验证上述结论,如表3所示,本文介绍了非参数统计学中的Wilcoxon检验[23]和Friedman检验[24]的统计结果。

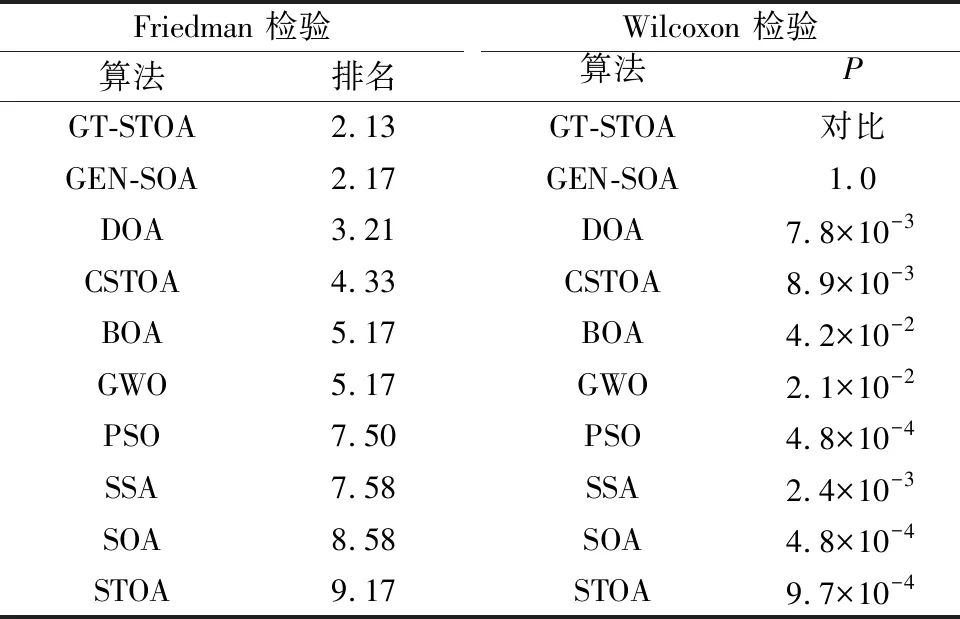
表3 统计检验结果

在Wilcoxon统计检验中,若显著性水平P<0.05,则表示算法对于对比算法具有显著性优势。而在Friedman统计检验中,将根据排名值进行排序,排名值越低则算法排名顺序越高。综上所述,在本文算法性能排名第一的是GT-STOA;同时,结合P值可知GT-STOA较9种对比算法而言具有显著的优势。

3.6 压力容器优化问题

为实际验证GT-STOA的优化效果,在前期算法取得出色收敛效果和寻优能力的前提下,采用压力容器优化设计问题对GT-STOA进行实例验证。其中种群规模设定为30,最大迭代次数设为1 000。

压力容器优化设计问题[25]是使一个圆柱形容器的材料、成型和焊接总成本最小化,该问题也同样具有4个主要优化变量,包括壳体厚度Ts(x1)、顶部厚度Th(x2)、内半径R(x3)、忽略顶部的圆柱形截面长度L(x4)。其中,压力容器的约束条件为以压力容器优化设计问题为例,通过应用GT-STOA与SOA、STOA和GEN-SOA算法进行收敛性分析,收敛曲线图如图3所示。同时,就GT-STOA与STOA于压力容器设计问题进行精度分析,其中所得最优解的变量取值与30次独立实验所得的平均精度如表4所示。

表4 压力容器检验结果

图3 压力容器优化问题

(17)

由此可见,GT-STOA不仅在上述分析的算法准确性和收敛速度上有明显的优势,而且在压力容器工程优化问题上也优于同型算法,拥有更出色的收敛与寻优能力,并较传统STOA算法的优化精度提升了42.54%。

4 结论

针对乌燕鸥优化算法(STOA)求解精度较低、种群多样性较弱,并且容易陷入局部最优的缺点,提出了一种融合混沌映射、自适应惯性权重与高斯变异的多机制乌燕鸥优化算法(GT-STOA)。其中,本文研究的创新点和主要贡献在于通过混沌映射函数的遍历性特征和随机性特征对种群初始位置进行多样性调整,增加了种群多样性,予以解决了由于种群多样性不足导致寻优效率低下的缺陷;并且基于自适应惯性权重和高斯变异优化机制对最优种群个体位置进行扰动,不仅增强了算法的稳定性,还能帮助算法跳出局部最优,提高算法在局部搜索过程的寻优精度和收敛速度。

与此同时,为验证GT-STOA算法的优越性和稳定性,在12个基于不同特征的基准测试函数上,分别对GT-STOA、GEN-SOA、BOA、SSA、GWO、PSO、DOA、STOA、SOA和CSTOA进行仿真实验对比。由实验数据可知,GT-STOA在9个测试函数上均找到理论最优值,寻及理论最优率为75%。并且在非参数统计检验中Friedman排名值为2.13位居第一,展现出了算法显著的优势。不仅如此,还通过引入了压力容器优化设计问题对GT-STOA算法进行了实例验证,据实验结果表明GT-STOA较传统STOA算法在优化精度上提升了42.54%。

未来,将进一步对STOA攻击寻优的方式进行深入的研究与分析,并努力将优化后的GT-STOA与实际工程应用问题相结合,投入在离散优化问题的改进与应用中,提升GT-STOA算法的实际应用价值。