基于标定线的轨道几何检测系统精度评定方法

郝晋斐 陈春雷 赵紫珅 贺雨 韩志 王宁

1.中国铁道科学研究院集团有限公司 基础设施检测研究所， 北京 100081； 2.北京铁科英迈技术有限公司， 北京 100081

轨道几何检测系统为提高轨道平顺性、保证列车运行安全和舒适发挥了重要作用［1］。工务现场养护维修水平的提升与检测数据分析应用的持续深化，对轨道几何检测系统精度提出了更高的要求。轨道几何检测系统精度评定方法对于准确表征系统技术状态、服务技术管理至关重要。

欧美等地区和国家围绕轨道几何检测系统精度评定开展了相关技术研究与专业试验线建设。欧洲EN 13848-2—2020《Railway applications-Track-Track Geometry Quality - Part 2: Measuring Systems - Track Recording Vehicles》已形成体系化的评定方法，采用JCGM 200：2012《International Vocabulary of Metrology-Basic and General Concepts and Associated Terms(VIM)》对试验中各引入不确定度分量进行评价。美国交通技术研究中心（Transportation Technology Center Inc.， TTCI）在其精确试验线上建成了轨道检查车动态标定区段，并基于标定区段开展了轨道几何动态静态比对、动态静态差异修正方法等方面的研究［2］。

长期以来，受限于无专业的标定线，我国专业检测车轨道几何检测系统精度评定试验主要在运营线路开展，无法准确掌握轨道动态静态差异。现行技术管理标准Q/CR 751—2020《铁路基础设施动态检测 轨道几何检测系统》采用静态复核方法验证系统精度，其中规定了精度评定的总体试验准则，但无具体操作方法，影响了评定结果的科学性和准确性。2021 年中国国家铁路集团有限公司立足轨道几何检测系统评定试验需求，开展了铁路基础设施检测设备标定线建设工作［3］。金振山等［4］参与了前期标定线专用扣件设计、轨道几何不平顺预设、标定线钢轨位移检测装置布置等试验研究工作，为轨道几何检测系统精度评定方法研究提供了良好的试验平台与研究基础。

基于前期轨道几何动态静态测量原理与轨道几何动态静态差异研究成果［5-6］，我国安装于专业检测车的轨道几何检测系统（主要为GJ-5 型、GJ-6 型检测系统）均采用惯性基准测量原理，对动态、有载条件下轨道几何状态进行测量，与静态测量在检测原理及被测对象上存在差异。为解决上述问题，本文选用轨道检查仪与钢轨位移测量装置，对静态轨道几何不平顺、轨道几何动态静态差异进行测量，通过轨道几何动态静态比对方法解决动态静态测量原理差异造成的部分参数无法直接比对的问题；通过轨道几何动态静态差异修正方法，对静态测量结果进行修正，形成精度评定参考值，确定有无载荷条件下轨道几何动态静态差异对精度验证的影响；采用测量不确定度分析方法，对各阶段测量引入的不确定度进行评价，最终形成静态测量结果与动态静态差异修正相结合的轨道几何检测系统精度评定方法。同时，选取标定线典型预设轨道几何不平顺工况，进行评定方法验证。

1 轨检系统精度评定方法

1.1 轨道几何检测系统校准模型

轨道几何检测系统精度评定方法具体选用设备、数据处理方法、试验流程见图1。

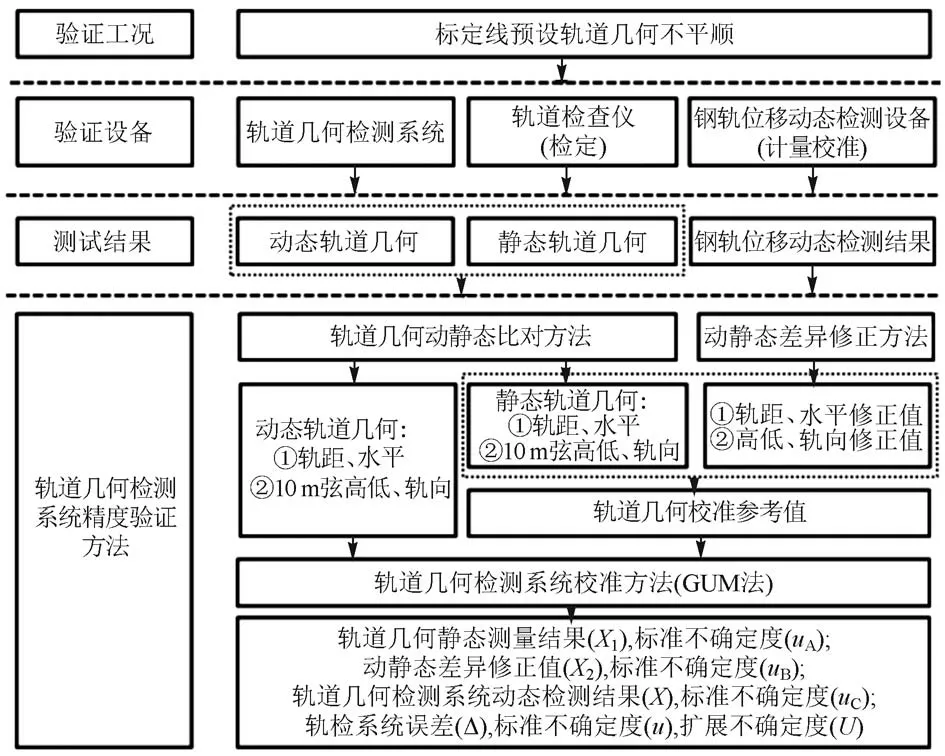
图1 轨道几何检测系统精度评定方法

轨道几何检测系统精度评定模型的表达式为

式中：Y为校准参考值。

校准模型参数X、X1、X2引入标准不确定度，依次记为uA、uB、uC。根据JJF 1059.1—2012《测量不确定度评定与表示》，采用测量不确定度A 类、B 类评定方法进行评价，并计算得到合成标准不确定度（u）与扩展不确定度（U）。

1）A类不确定度分析方法

该方法是基于统计分析方法对观测条件下测得的量值进行测量不确定度的估计。以n次轨道几何检测系统重复测量为例，xi为第i次测量值，采用测量结果算术平均值作为动态检测结果（X），即

根据A 类不确定度分析方法，xi与X对应的单次测量标准差（s）与标准不确定度（uA）分别表示为

式中：xmax、xmin分别为动态测量结果中的最大值和最小值；cn为极差法求解标准差中的级差系数。

2）B类不确定度分析方法

该方法是用不同于观测值进行统计分析的不确定度评定方法。以uB为例，其表达式为

式中：Δnmax为轨道检查仪最大允许误差，即测量值的分布区间半宽度；k为包含因子。

3）合成不确定度

合成不确定度是对各标准不确定度分量的合成。以校准过程合成不确定度求解为例，u的表达式为

4）扩展不确定度

为合理赋予被测量以较高的包含区间半宽度，通常在合成不确定度的基础上乘以包含因子，形成扩展不确定度。以本次评定为例，U的表达式为

式中：k1为包含因子。

通常k1= 2，置信区间为95%。

1.2 动态静态检测结果比对与修正方法

1）高低、轨向

高低、轨向参数的动态静态检测采用不同的测量原理与数据输出形式。轨道几何检测系统动态测量中，高低、轨向参数输出结果为波长1.5 ～ 42 m、1.5 ～70 m、1.5 ～ 120 m 的空间曲线［7］，在波长范围内检测系统传递函数理论上恒为1。

轨道检查仪目前被广泛应用于轨道几何静态测量，主要采用陀螺轨迹法，通过对陀螺摇头、点头角速率的积分获取轨道平面和高程信息［8］。轨道几何静态管理中，高低、轨向参数采用弦测法方式进行表征。以静态高低参数的中点弦测量为例，其测量模型（yk）与传递函数［H(ω)］表达式分别为

式中：hk、hk-p、hk+p分别为测量点里程k、k-p、k+p位置的轨道高程，p为测量半弦长；ω为空间角频率，ω=2π/λ，λ为轨道不平顺波长。

根据式（10），传递函数随波长在0 ～ 2 变化。不同波长传递函数不同，导致部分波长段不平顺幅值放大，部分波长段不平顺幅值缩小，甚至在某些特征波长区段，传递函数为0［5］。

高低、轨向动态测量是对管理波长范围内轨道几何不平顺的数学表征，无法在现场复现。静态测量采用弦测法表征轨道几何不平顺，检测原理明晰，现场实测可复现。因此，从精度评定适应性角度出发，选用TG/GW 102—2019《普速铁路线路修理规则》规定的10 m 弦方式进行高低、轨向参数的动态静态比对，将轨道几何检测系统与轨道检查仪检测结果均按照式（9）进行10 m 弦数据转换，处理后结果作为校准模型的动态静态检测结果。

在轨道几何检测系统检测过程中，钢轨受荷载作用，垂向、横向均会产生动态位移。该位移包括轨道结构刚度均匀且平顺性良好情况下钢轨均衡位移和因轨道几何不平顺导致轮轨力加剧而造成的附加钢轨位移。以钢轨垂向均衡位移为例，轨道结构刚度均衡且平顺性良好条件下，可将轨道简化为连续弹性支撑梁模型，钢轨抗弯刚度为EIx，单位长度支撑弹性系数为k2，则动态检测过程中钢轨垂向位移（y）表征为

根据其边界条件以及受力特性，车辆在运行过程中钢轨位移恒为定值，动态检测中该不平顺波长为无限长，不会被检测系统测得。因此，高低、轨向动态测量是对静态几何不平顺与附加钢轨位移叠加的轨道几何动态不平顺进行测量。

标定线钢轨位移总体均衡稳定的前提下，采用在高低、轨向整个不平顺工况范围内连续布置钢轨位移检测设备的方式，掌握附加钢轨位移，并用不平顺范围内钢轨位移差异变化量（Δy）表征，即

式中：x1、x2、…、xn依次为校准工况n个钢轨位移测量装置测得的垂向或横向位移。

在校准过程中，将高低、轨向动态静态差异修正值设置为0，将附加钢轨位移对校准过程的影响换算为uC的一个分量，纳入到不确定度分析。具体方法为根据Δy，按照式（6）对该不确定度分量进行评价。

2）轨距、水平

轨道几何动态静态检测中，轨距、水平参数具有相同的定义方式，可直接进行比对，因此轨距、水平的动态静态测量结果即为校准模型动态静态测量结果。X是在X1基础上叠加了钢轨动态位移。采用在轨距、水平校准点位置安装横向、垂向钢轨位移测量装置的方式，按式（13）、式（14）分别形成轨距、水平动态静态差异修正值（X2，G、X2，C）。对应uC需通过分别位于右股钢轨、左股钢轨的a、b 两个校准点钢轨位移测量不确定度合成。

式中：xa、xb分别为a、b 两个校准点的钢轨横向或垂向位移，钢轨横向轨距扩大为正，反之为负，钢轨垂向轨距与高低定义方向相同。

2 轨检系统精度评定试验

2.1 试验工况与试验设备

在标定线选取轨道几何不平顺幅值变化率最大的高低、轨向工况进行评定方法验证。

1）工况1：幅值6 mm、波长5 m 的右高低工况。工况内间隔1 个轨枕选取校准点，标号为1#—6#测点；工况外轨道几何平顺区段设置7#测点。这7个测点布置钢轨垂向位移检测设备。

2）工况2：幅值8 mm、波长10 m 的轨向工况。工况内间隔4 轨枕在左右股选取校准点，标号为左右8#—10#测点；工况外轨道几何平顺区段设置左右11#测点。这8个测点布置钢轨横向位移检测设备。

试验工况、钢轨位移测点布置见图2。

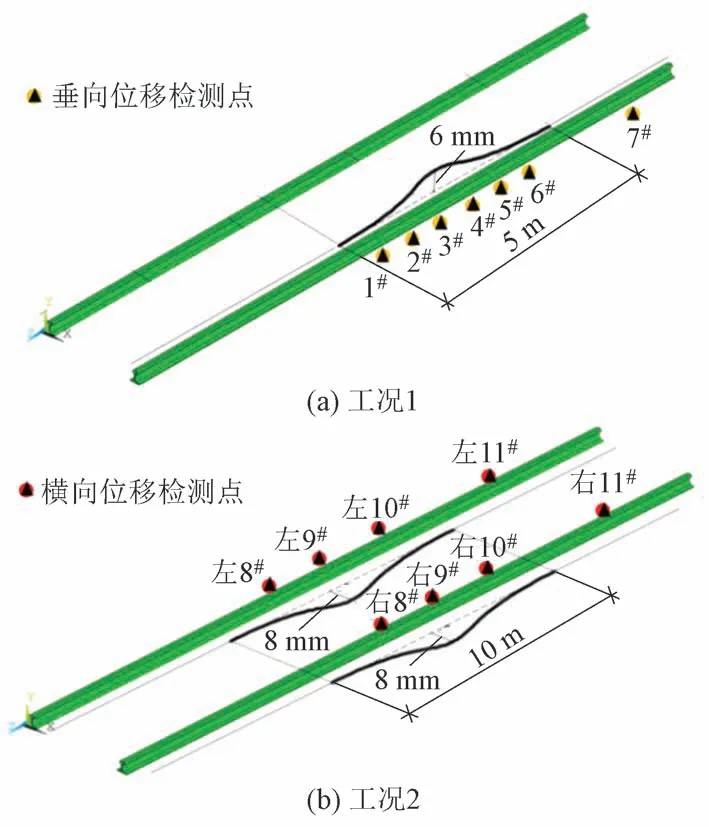
图2 校准点及钢轨位移测点布置

试验中，选取被工务现场广泛使用且纳入JJG 1091—2013《铁路轨道检查仪检定台检定规程》管理的GRP1000IMS 型轨道检查仪，其高程、平面、轨距最大允许误差分别为±1.0、 ±1.0、 ±0.3 mm。钢轨位移动态测量设备试验前进行校准送检，最大允许误差±0.03 mm。

2.2 动态静态检测数据分析

某检测车搭载GJ-6 型轨道几何检测系统对标定线进行n= 5次动态检测，速度等级为80 km/h，测量结果见图3。

图3 标定线5次动态测量结果

利用轨道检查仪对标定线进行1次静态测量。数据经动态静态检测结果比对方法处理，形成高低、轨向、轨距、水平校准模型动态静态检测结果，见图4。

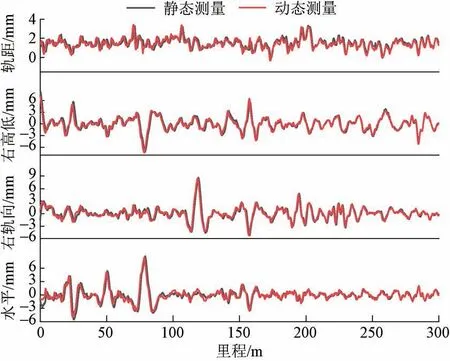
图4 轨道几何动态静态测量数据处理结果

轨道几何检测系统n= 5次测量结果按照式（3）形成动态检测结果（X），标准不确定度（uA）按式（4）、式（5）进行计算，级差系数cn= 2.33。静态测量中，标准不确定度（uB）按式（6）进行计算，轨道检查仪在最大允许误差范围内采用均匀分布假设，k=。各校准点X、X1及uA、uB见表1。

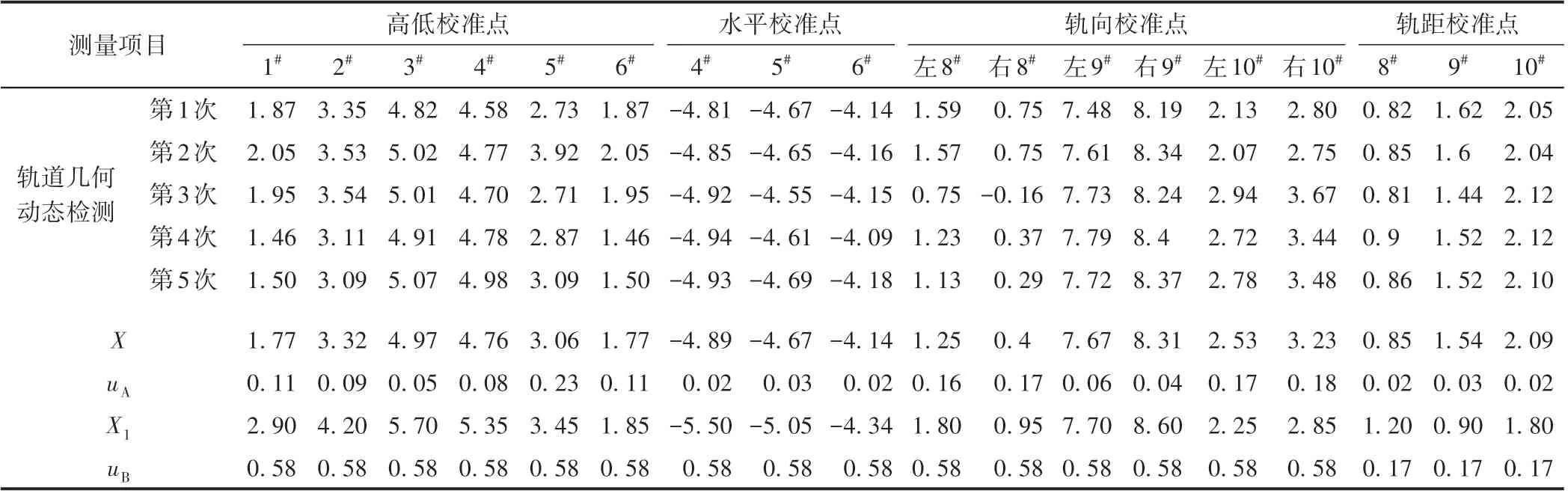
表1 轨道几何检测系统校准点动态静态检测结果与标准不确定度

2.3 动态静态差异修正值提取

为提取高低、轨向动态静态差异修正值，利用钢轨位移动态检测设备对检测车通过时各测点钢轨动态位移进行测量。测量结果见表2。

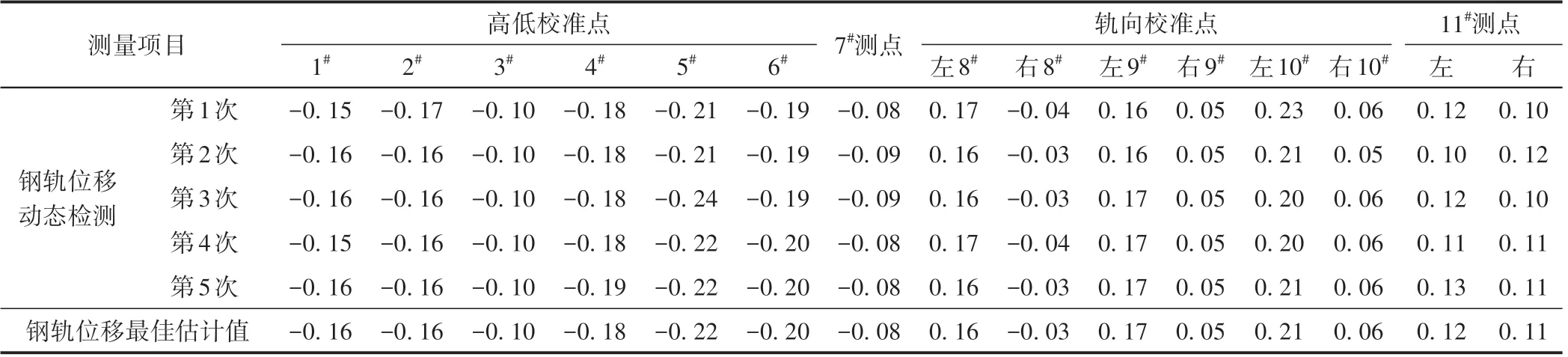
表2 各测点钢轨位移动态测量结果

基于高低、轨向动态静态差异修正方法，先将X2设置为0，再利用各测点钢轨动态位移，将附加钢轨位移纳入到不确定度分析中。uC包括如下3个不确定度分量。

①钢轨位移多次重复测量引入的不确定度（u1）。采用A 类标准不确定度分析方法，按式（4）、式（5）进行评价，n= 5次测量过程，cn= 2.33。

②钢轨位移动态测量设备引入的不确定度（u2）。Δnmax= 0.03 mm，采用B 类标准不确定度分析方法，按式（6）进行评价，k=。

③附加钢轨位移引入的不确定度（u3）。高低、轨向测点内钢轨位移差异变化量按式（12）进行计算，Δy= 0.14 mm，采用B 类评定标准不确定度分析方法，按式（6）进行评价，k=。

最终，高低、轨向动态静态差异修正引入标准不确定度（uC），合成方法为

在轨距动态静态差异修正中，xa、xb分别为左右8#—10#测点的钢轨横向位移，按式（13）计算形成修正值；在水平动态静态差异修正中，xa为右股钢轨校准测点4#—6#垂向位移，xb为7#测点表征的左股轨道几何平顺区段钢轨垂向位移，按式（14）计算形成修正值。uC由xa、xb各自引入u1、u2合成，分别记为ua1、ua2，ub1、ub2，标准不确定度（uC）合成方法为

各校准点X2、uC以及各校准环节u1、u2、u3见表3。

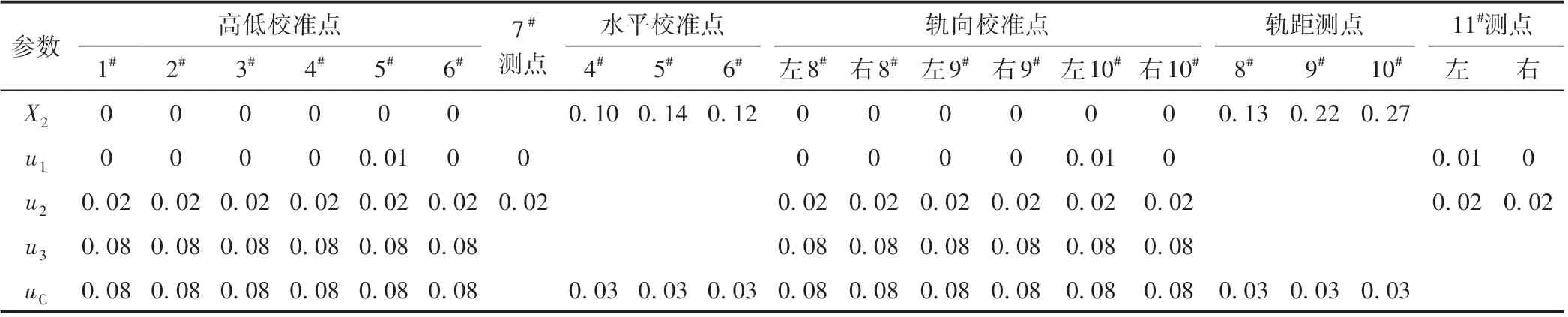
表3 各校准点动态静态差异修正值与标准不确定度

2.4 误差及不确定度评定

基于轨道几何检测系统精度验证过程各校准点动态测量值（X）、静态测量值（X1）、动态静态差异修正值（X2），以及引入标准不确定度（uA、uB、uC），按式（1）、式（2）、式（7）、式（8）计算轨道几何检测系统误差（Δ）及合成不确定度（u）、扩展不确定度（U），结果见表4。可知：在U的各合成分量中，uB占比最大，可达uA、uC的5倍以上。。

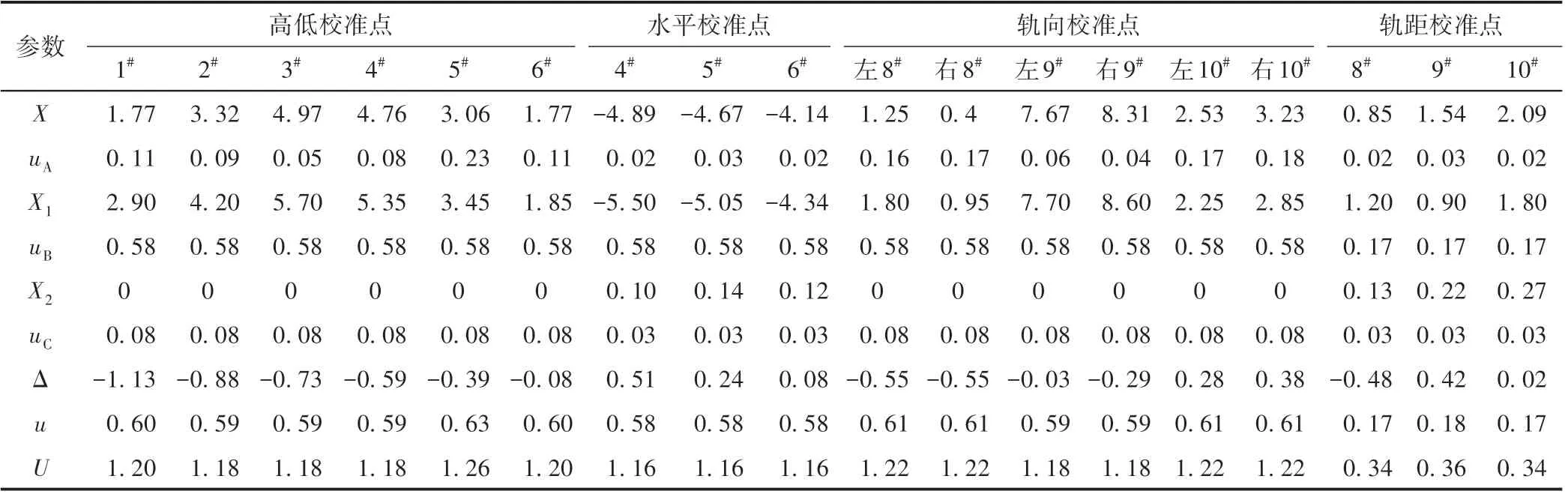
表4 轨道几何检测系统精度验证各校准点误差与不确定度

3 结论

本文首次采用轨道动静态检测结果比对与差异修正相结合的方法，结合误差及不确定度评定，实现轨道几何检测系统精度的准确评价，并通过广泛应用的轨道检查仪、钢轨位移检测设备开展验证试验。主要结论如下：

1）轨检系统高低、轨向、水平参数误差总体上在0.50 ～ 0.80 mm，扩展不确定度约为1.20 mm（k= 2）；轨距参数误差总体上在0.40 mm 左右，扩展不确定度约为0.40 mm（k= 2）。

2）在扩展不确定度（U）各合成分量中，由静态测量引入的标准不确定度（uB）占比最大，可达动态测量标准不确定度（uA）、动态静态差异修正值标准不确定度（uC）的5倍以上。

利用本文提出的轨道几何检测系统精度评定方法，通过选用高精度静态测量设备，可以进一步降低评定过程中引入的不确定度，提升精度评定能力。