考虑几何非线性的大跨度斜拉桥车-桥耦合系统地震响应分析

2023-10-09李永亮乔宏徐曼李克冰王辰羽龙佩恒

铁道建筑 2023年8期

李永亮乔宏，2 徐曼李克冰王辰羽龙佩恒

1.北京建筑大学土木与交通工程学院，北京 102616； 2.北京建筑大学工程结构与新材料北京高等学校工程研究中心，北京 102616； 3.中冶建筑研究总院有限公司，北京 100088； 4.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081

地震作用下，车-桥耦合振动分析不是结构地震响应和车-桥耦合动力响应简单叠加。近年来，各国学者从模型建立、轮轨关系模拟、地震作用施加等方面进行了深入研究。文献［1-5］大多以连续梁桥、连续刚构桥等传统高速铁路桥梁形式为研究对象，对大跨度铁路斜拉桥相关研究较少。熊建珍等［6］以大跨度斜拉桥天兴洲长江大桥为背景，建立了地震作用下车-桥耦合振动分析模型，分别研究了货车、中速旅客列车和高速旅客列车过桥时的行车安全性。Zhang等［7］以一座钢桁梁斜拉桥为算例，以实测地震波——天津波为输入地震波，利用大质量法研究了多点地震激励下车-桥耦合系统的动力响应。雷虎军等［8］以一座主跨432 m 的斜拉桥为工程背景，基于谱方法人工合成空间相关的多点地震动，研究了行波效应、场地效应、失相干效应对车-桥耦合系统地震响应的影响。郭文华等［9］基于ANSYS 和SIMPACK 联合仿真分析平台，以一座双塔双索面斜拉桥为算例，研究了地震强度和黏滞阻尼器参数对车桥动力响应的影响。

与跨越能力有限的梁式桥不同，由于斜拉索的存在，大跨度斜拉桥受到非线性的影响更加显著。在拉索垂度效应、结构大变形等几何非线性因素影响下，动力荷载（如地震作用、列车荷载）下的桥梁响应通常呈现出中小跨度没有的非线性特性［10］。然而，关于地震作用下车-桥耦合动力分析时考虑几何非线性因素的文献却十分有限，对大跨度斜拉桥车-桥耦合系统地震响应的影响规律尚未探明。

本文以一座超千米公铁两用斜拉桥为工程背景，基于全过程迭代法，考虑几何非线性因素的影响，对地震作用下车-桥耦合振动进行分析，研究几何非线性、列车速度等因素对耦合系统动力响应和行车安全性的影响。

1 考虑几何非线性的斜拉桥-列车耦合系统地震响应分析模型

1.1 桥梁模型

基于有限元软件建立大跨度斜拉桥有限元模型，并在分析中考虑几何非线性的影响。斜拉桥的几何非线性影响因素主要可概括为垂度效应、大变形效应和梁柱效应［11］。

采用Ernst 公式修正斜拉索的弹性模量来考虑垂度效应的影响，即

式中：Eeq为拉索计算垂度效应后的弹性模量；E0为拉索初始弹性模量；γ为拉索重度；S为拉索长度；α为拉索的水平夹角；σ为拉索应力。

通过在结构运动方程设置可变的刚度项，考虑大变形效应和梁柱效应的影响。结构的运动方程为

式中：Mb、Cb、Kb分别为桥梁质量矩阵、阻尼矩阵和刚度矩阵；Fb为荷载向量；Xb为桥梁的位移向量。

Kb与Xb相关，由结构自身的弹性刚度矩阵（KE）和随位移变化而改变的几何刚度矩阵（KG）组成，即

为了考虑几何非线性的影响，在动力响应时程分析时需在每个时间步计算完成后重新计算结构的位移和内力，从而得到新的刚度矩阵，用于下一时间步的计算。

1.2 列车模型

将组成列车的每一节车辆分解为车体、转向架和轮对三种基本构件并视为刚体，三种构件通过包含弹簧和阻尼元件的悬挂装置连接，如图1所示。

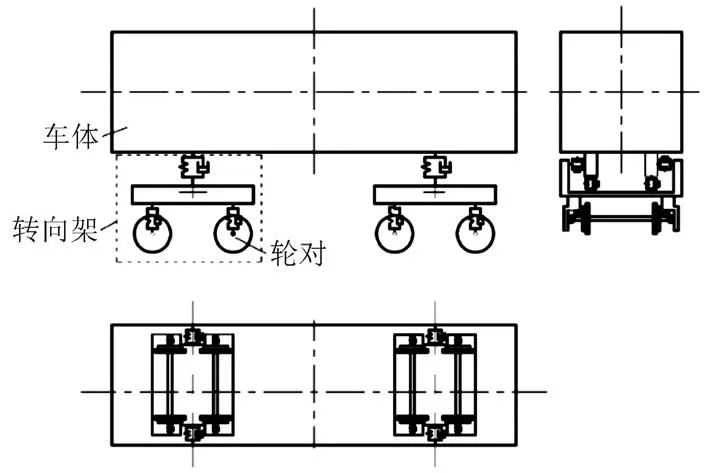
图1 车辆计算模型

车体、转向架及轮对均具有伸缩振动、横摆振动、沉浮振动、侧滚振动、点头振动和摇头振动共6个自由度。为简化分析，假定列车匀速通过桥梁，并忽略车体、转向架和轮对沿纵轴方向的振动，此时，单节车辆的自由度为35个。基于多刚体动力学建立车辆模型，可以得到列车子系统的动力平衡方程［12］

式中：Mv、Cv、Kv分别为列车质量矩阵、阻尼矩阵和刚度矩阵；Xv和Fv分别为列车的位移向量和所受荷载向量。

1.3 基于全过程迭代法的耦合系统地震响应分析

考虑几何非线性的大跨度斜拉桥车-桥耦合系统地震响应分析，将地震作用视为外荷载施加于桥梁子系统，地震作用对列车子系统的影响通过轮轨关系实现。地震作用下大跨度斜拉桥-列车耦合系统的运动方程可以表示为

式中：Fvb为车辆对桥梁的作用力；Fbv桥梁为对车辆的作用力；为地震作用力。

基于全过程迭代法［13］求解地震作用下耦合系统的动力响应：桥梁子系统和列车子系统的地震响应分别通过ANSYS 软件和Matlab 平台求解。在迭代计算过程中，通过人为干预迭代过程促进计算收敛，提高计算效率。具体计算流程见图2。

图2 计算流程

1）在MATLAB 中建立列车子系统的计算模型，在ANSYS 中建立桥梁子系统的计算模型，选取地震作用和轨道不平顺。

2）假定桥梁子系统在列车上桥前的位移为0，将轨道不平顺以外荷载的形式输入列车模型，采用Newmark-β法，计算得到列车通过桥梁全过程的车辆的动力响应和轮轨力时程。

3）将第2步中得到的车辆轮轨力时程通过轮轨接触关系转为桥梁节点力，与地震荷载共同输入桥梁子系统，通过桥梁矩阵计算公式得到列车通过桥梁全过程的桥梁铁路桥面各节点非线性响应。

4）将第3步中得到的桥梁各节点动力响应与对应位置钢轨的轨道不平顺进行叠加，计算出列车子系统的新激励源。

5）将第4 步中新激励输入列车子系统，得到列车通过桥梁全过程的新的车辆动力响应。

6）将第5步中得到的车辆轮轨力时程与第2）步中的车辆轮轨力时程进行对比，计算两者的差值。

7）判断轮轨力差值是否满足设定的轮轨力收敛条件，若满足则计算结束，输出车桥系统的动力响应结果。反之，以第5步中轮轨力作为新的激励源，重复第2—第6步。

2 工程背景与计算条件

2.1 工程概况

双塔三索面公铁两用斜拉桥跨径布置为（140 +462 + 1 092 + 462 + 140） m。上层为6车道高速公路，下层为4线铁路，结构总体布置如图3所示。

图3 斜拉桥总体布置（单位：m）

桥梁主梁为N 形桁架，共有间距为14 m 的164 个节间，宽度为35 m，边桁和中桁的中心高度分别为16.0、16.3 m。主桁采用500、420、370 MPa 三种规格的高强度桥梁结构钢材。其中，桥塔两侧各4个节间采用500 MPa 高强度结构钢；相邻的主跨侧、边跨侧各3个节间采用420 MPa钢材；其余112个节间及横联杆件均用370 MPa 钢材；桥塔（墩）的材料为钢筋混凝土，混凝土强度等级为C60；斜拉索材料为平行高强度钢丝，等级为2 000 MPa 级，钢丝采用铝锌合金镀层的高强度、低松弛钢丝，直径为7 mm。

2.2 桥梁自振特性

基于ANSYS 软件建立桥梁有限元模型。采用Beam188 单元模拟主梁和倒Y 形桥塔（墩）；采用Shell181 单元建立简化桥面板模型；采用Link10 单元模拟斜拉索。该桥为纵向漂浮体系，因此在主梁与桥墩桥塔之间不设纵向约束，仅设置横桥向和竖桥向约束；桥塔（墩）与场地之间为固定约束。为了提高计算效率，考虑到黏滞阻尼器可以有效减小斜拉桥的地震响应［14-15］，在建模分析时偏保守地忽略了纵向阻尼器的影响。斜拉桥有限元模型如图4所示。

图4 斜拉桥有限元模型

建模时考虑拉索预应力效应和垂度效应的影响，可以得到斜拉桥前15阶频率和振型，如表1所示。

表1 桥梁自振频率及振型

将桥梁的前5 阶振型及自振频率与文献［16-17］进行对比，从而验证模型的有效性，对比结果见表2。可知，除纵飘外，本文桥梁模型各主要振型对应的自振频率与文献结果差异率在6%以内。纵飘是大跨度桥梁常见低频振型，符合文献［10］中的客观规律，故认为本文模型有效。

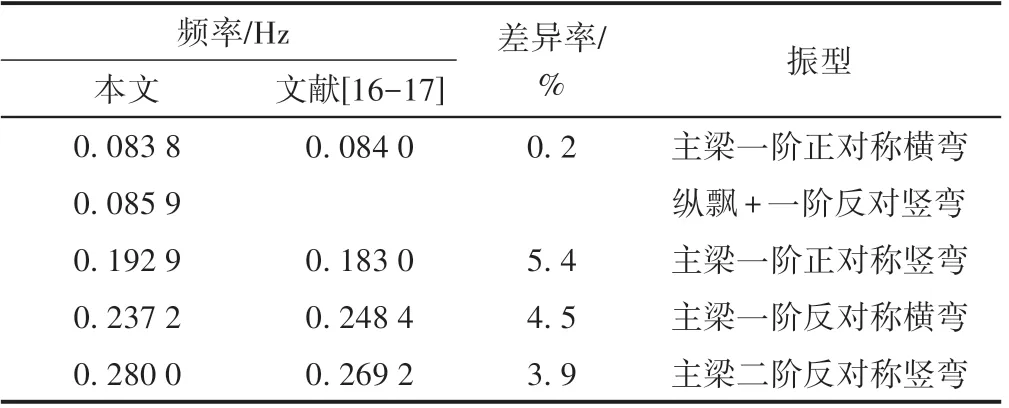
表2 振型及频率对比

2.3 地震激励参数

桥梁所在地抗震设防烈度为六度，场地土类型别为Ⅱ类，特征周期值为0.4 s，依据反应谱曲线在美国太平洋地震工程研究中心的强震数据库中选出最合适的实测地震波，其位移及加速度时程曲线如图5 所示。同时输入横桥向和竖桥向位移时程，竖向位移峰值取横向位移峰值的1/2。

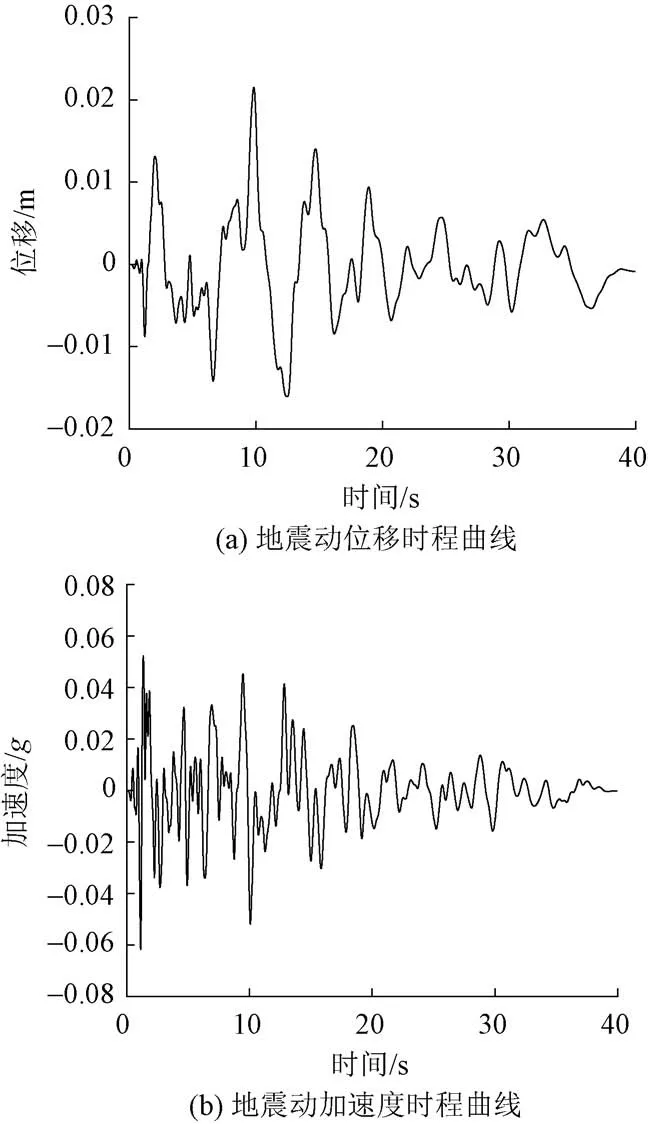
图5 地震动特性

2.4 车辆参数与轨道不平顺

列车模型采用16 节编组为3 动1 拖的CRH2高速铁路列车，轨道不平顺采用德国低干扰谱。车辆参数及轨道不平顺参数按文献［12］取值。

3 计算结果

考虑几何非线性因素的影响，计算分析大跨度斜拉桥车-桥耦合系统的地震响应及行车安全性。设置时间步长为0.01 s，收敛条件为相邻两次迭代之间的轮轨力差值不大于10 N。

3.1 几何非线性对耦合系统地震响应的影响

考虑斜拉桥几何非线性的三个影响因素，分析时设计5种工况：①地震作用下不考虑非线性因素的车-桥耦合系统动力响应分析；②地震作用下仅考虑垂度效应的车-桥耦合系统动力响应分析；③地震作用下仅考虑梁柱效应的车-桥耦合系统动力响应分析；④地震作用下仅考虑大位移效应的车-桥耦合系统动力响应分析；⑤地震作用下同时考虑垂度效应、梁柱效应及大位移效应的车-桥耦合系统动力响应分析。不同工况下斜拉桥的主梁跨中位置动力响应峰值和列车运行平稳性及安全性指标峰值分别见表3和表4。

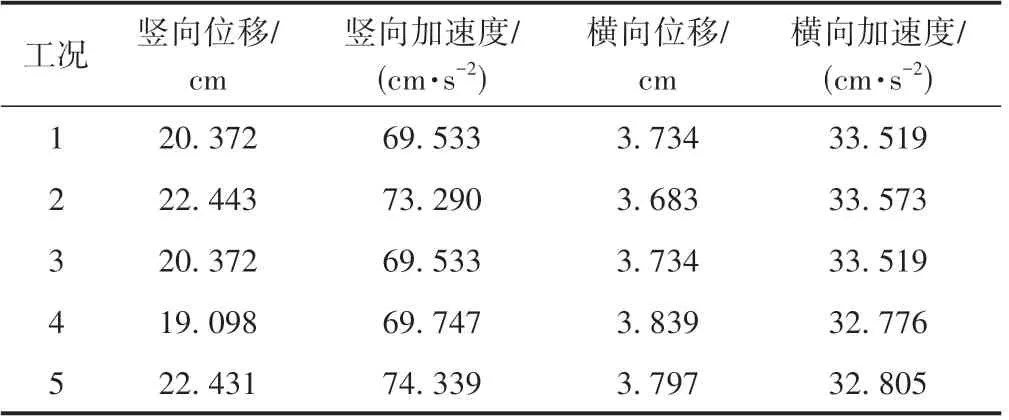
表3 不同工况下斜拉桥的主梁跨中位置动力响应峰值

表4 不同工况下列车运行平稳性及安全性指标峰值

由表3和表4可知：

1）与工况1 相比，工况5 的主梁跨中竖向位移增加了10.11%，竖向加速度增加了6.91%；主梁跨中位置横向位移和横向加速度增加均不足2%。这说明考虑几何非线性因素的影响后，斜拉桥主梁跨中位置的竖向动力响应峰值增大。几何非线性因素对桥梁竖向动力响应的影响较为显著，对列车运行安全性指标也有一定影响，若忽略则有可能导致行车评估结果偏于不安全。

2）与工况1 相比，工况2 垂度效应影响下桥梁跨中竖向位移增加了10.17%，横向位移减小了1.37%，车辆竖向加速度增加了8.49%；工况3桥梁跨中横、竖向位移和列车竖向加速度无变化；工况4 桥梁跨中竖向位移减小了6.25%，横向位移增加了2.81%，车辆竖向加速度增加了1.85%。这表明斜拉桥几何非线性的三个影响因素中，垂度效应对耦合系统动力响应的影响最大，大位移效应次之，梁柱效应最小，仅考虑梁柱效应时，桥梁和列车的动力响应峰值不受影响。

3.2 列车车速对耦合系统地震响应的影响

假定列车的行驶速度分别为150、175、200、225、250 km/h，考虑几何非线性的影响，研究不同车速对耦合系统地震响应的影响。不同车速下斜拉桥和车辆动力响应峰值见表5。

表5 不同车速下斜拉桥和车辆动力响应峰值

由表5可知：

1）随着车速的增大，桥梁跨中竖向位移峰值和竖向加速度峰值整体上呈逐渐增大的趋势，车速对桥梁子系统的地震响应有一定影响。

2）随着车速的增大，列车轮重减载率、脱轨系数逐渐增加。车速为250 km/h 时脱轨系数为0.530，满足安全性要求。车速为225 km/h 时轮重减载率达到0.710，指标评价为危险；车速为250 km/h 时达到0.858，理论上超过安全阈值。这可能与分析时选用的轨道不平顺谱为德国低干扰谱有关。相关研究表明［18］，关于车辆安全性的脱轨系数、轮重减载率等指标，中国高速谱明显优于德国低干扰谱。