考虑环缝接头水力劣化的盾构隧道渗漏数值分析

周建 ，张晓 ，蒋熠诚

（1.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江省城市地下空间开发工程技术研究中心（浙江大学），浙江 杭州 310058）

近年来，东南沿海城市快速发展，以盾构隧道为主要形式的地铁隧道、海底隧道、越江隧道已被大量建设［1-2］.盾构隧道是一个三维结构，由管片通过螺栓拼接而成，管片间分布着许多纵缝以及环缝接头，现场调查揭示管片接头是防水薄弱部位［3-4］.地下水通过管片间的接头渗入隧道内部，不仅会导致洞周土体孔压降低，诱发隧道的长期沉降，还会导致管片张开，甚至会引发漏泥、漏砂病害，严重影响隧道运营安全［5-6］.因此，研究盾构隧道接头渗漏诱发的地层以及结构响应具有重要的工程意义.

对于隧道渗漏所诱发的影响，学者们开展了深入的研究.早期研究人员往往假设隧道是均匀渗漏的，研究发现衬砌相对于土的渗透性越大，则渗漏造成的影响越剧烈［7-9］.刘印等［10］基于平面应变假设，模拟了不同位置纵缝接头的渗漏，并指出接头渗漏与均质渗漏的显著不同.徐国文等［11］考虑了纵缝接头抗弯刚度的非线性特征，研究发现接头刚度对隧道结构内力影响显著.Zhou 等［12］假设接头渗透系数与接触应力的关系服从Louis 公式，实现了纵缝接头渗漏的动态演化分析，研究指出外拱的接缝开口相对内拱更加危险.彭益成等［13］在实现纵缝接头渗漏的动态演化分析时，还基于开发的接头联接单元模拟了衬砌接头的力学变形响应.

在实际工程中，由于隧道纵向刚度小，环缝接头更易张开.Zhang 等［14］对某盾构隧道的监测数据显示环缝接头渗漏占到全部渗漏位置的60%～70%.回顾已有的研究发现，学者们对纵缝接头渗漏的研究较为深入，然而对环缝接头渗漏的研究较少.李翔宇等［15］利用FLAC3D 软件，对纵向渗漏开展研究，发现隧道不均匀沉降随渗漏程度的增大而加剧.Wu等［16］开发了一维渗漏单元，对隧道的环缝以及纵缝渗漏进行了研究.上述研究多基于常渗透系数假设，认为随着渗漏的发展，衬砌接缝处的渗透性始终不变，忽略了环缝渗漏与隧道纵向沉降变形的长期劣化过程.隧道渗漏问题是一个动态演化过程［5］，环缝接头初始张开量较小，渗透性弱，但随着渗漏病害的加剧，环缝接头逐渐张开，渗透性逐渐加强.因此，亟须建立更加符合实际的环缝接头渗漏动态劣化模型，以反映真实的渗漏影响.

对此，本文基于渗流立方定律，依据隧道环缝接头张开量，建立了“接头渗透系数-接头张开量-纵向曲率半径”的迭代关系，实现了环缝接头动态劣化计算.利用该方法对盾构隧道环缝接头渗漏开展了三维有限元数值模拟，分析考虑动态演化后地表沉降变形、隧道纵向变形的发展规律，并分析了环缝接头密封圈的止水作用.

1 环缝动态劣化计算方法

1.1 环缝接头渗透系数与纵向曲率半径

盾构隧道在纵向上会呈现刚体转动变形，各衬砌环绕同一圆心发生小角度刚体转动，外拱处管片张开，内拱处管片闭合，地下水通过张开的缝隙渗入隧道.刚体转动大小可用隧道纵向曲率半径加以描述，如图1 所示，隧道的纵向沉降曲线为s=s(y)，则曲率半径R为：

图1 隧道曲率半径示意图Fig.1 Diagram of tunnel curvature radius

参考郑永来等［17］的研究成果，接头最大张开量与曲率半径的关系如式（2）：

式中：x=rsinφ，r为隧道半径，φ为中性轴角度，与螺栓刚度以及管片混凝土刚度等因素相关；R为隧道纵向曲率半径；ls为一环衬砌的长度；δj为接头螺栓的最大张开量，即接头最外侧的张开量.

然而在隧道发生纵向变形时，如图2 所示，环缝接头并非均匀张开，而是呈外拱处张开较大，内拱较小的模式.

图2 隧道纵向变形Fig.2 Longitudinal deformation of tunnel

此时，可认为接头张开量如图3 所示沿着深度线性分布，最大的接头张开量bmax=δj，则平均张开量为：

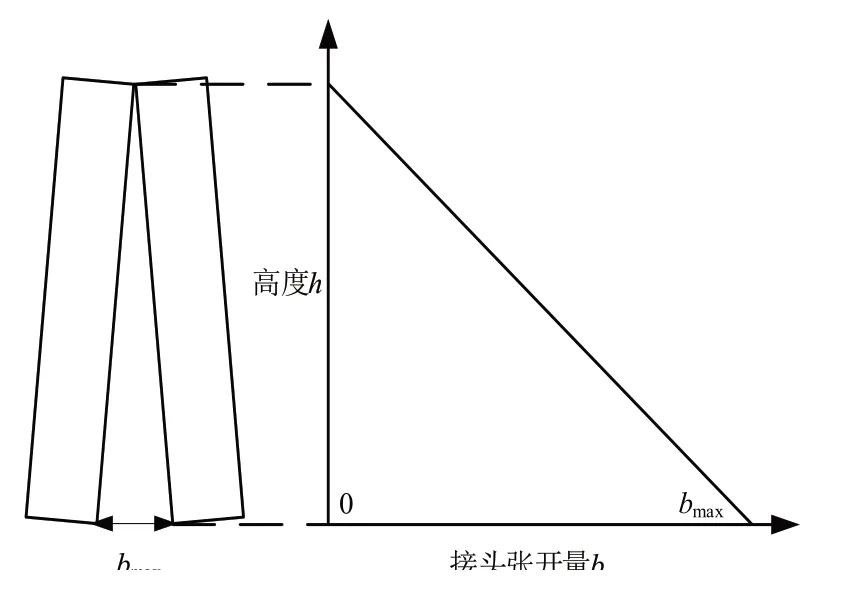
图3 管片接头张开示意图Fig.3 Diagram of segment joint opening

在隧道发生环缝渗漏时，地下水往往通过环与环之间的接头渗入隧道内部，将衬砌的环缝接头类比为岩石中的裂缝，接头的平均张开量即为裂缝宽度.由此，隧道环缝接头的渗透系数与张开量的关系可以应用立方定律［式（4）］求解［18］.立方定律最初由布辛习涅斯基提出，后被广泛应用于岩体裂缝渗流［19］.

由式（4）可推出环缝接头的平均渗透系数为：

式中：q为裂缝的单宽流量；γ为流体容重；μ为流体的动力黏滞系数；i为水力梯度；为环缝接头的平均渗透系数；为接头平均张开量，由式（3）所得.

1.2 止水密封垫的影响

渗流立方定律是基于光滑的裂缝面推导得到的，然而在盾构隧道中，接头与接头间并非平滑的裂缝，如上海地铁1 号线盾构隧道在管片接头位置采用嵌入式遇水膨胀橡胶做止水处理.为了考虑隧道环缝接头间止水措施的影响，本文引入接头渗透性折减系数η，折减后接头的渗透系数为：

式中：kre为考虑止水措施后的折减渗透系数；η为折减系数，范围在0～1.

目前关于盾构隧道接头张开后的渗透性变化规律研究较少，η值难以量化判断.按照地铁隧道的设计要求，隧道环缝接头的张开量不允许超过6 mm，因此，本文认为接头平均张开量为6 mm 时，防水完全失效，折减系数η为1，而接头平均张开量为0 时，接头的防水措施完好，折减系数η为0.平均张开量在0～6 mm 时，折减系数与接头平均张开量的关系更为复杂，在接头张开的初期，止水橡胶密封垫会持续膨胀，接头依然具有较好的止水性能，当接头张开量达到一定量值后，止水垫才会全面失效.由于缺乏相关的试验与理论研究，止水垫的防水能力随张开量的变化无法精确界定，本文假设折减系数与接头平均张开量呈线性变化关系，见式（7）.该公式可以反映接头张开量越大，渗透性能越好的规律，具有一定的合理性.

将式（7）代入式（6），可得接头折减渗透系数kre与接头平均张开量的关系.

综合式（1）、式（3）及式（8），即可实现接头渗透系数的动态劣化计算，详细的流程如图4 所示.首先，赋予接头初始渗透系数，计算初始时刻隧道渗漏情况并提取沉降数据；随后，依次计算隧道曲率半径Ri、接头平均张开量以及接头折减渗透系数kre；接下来，将所求得的渗透系数在材料参数中更新，并进入下一时间步的计算；反复迭代，直至达到计算年限Tmax时终止计算.

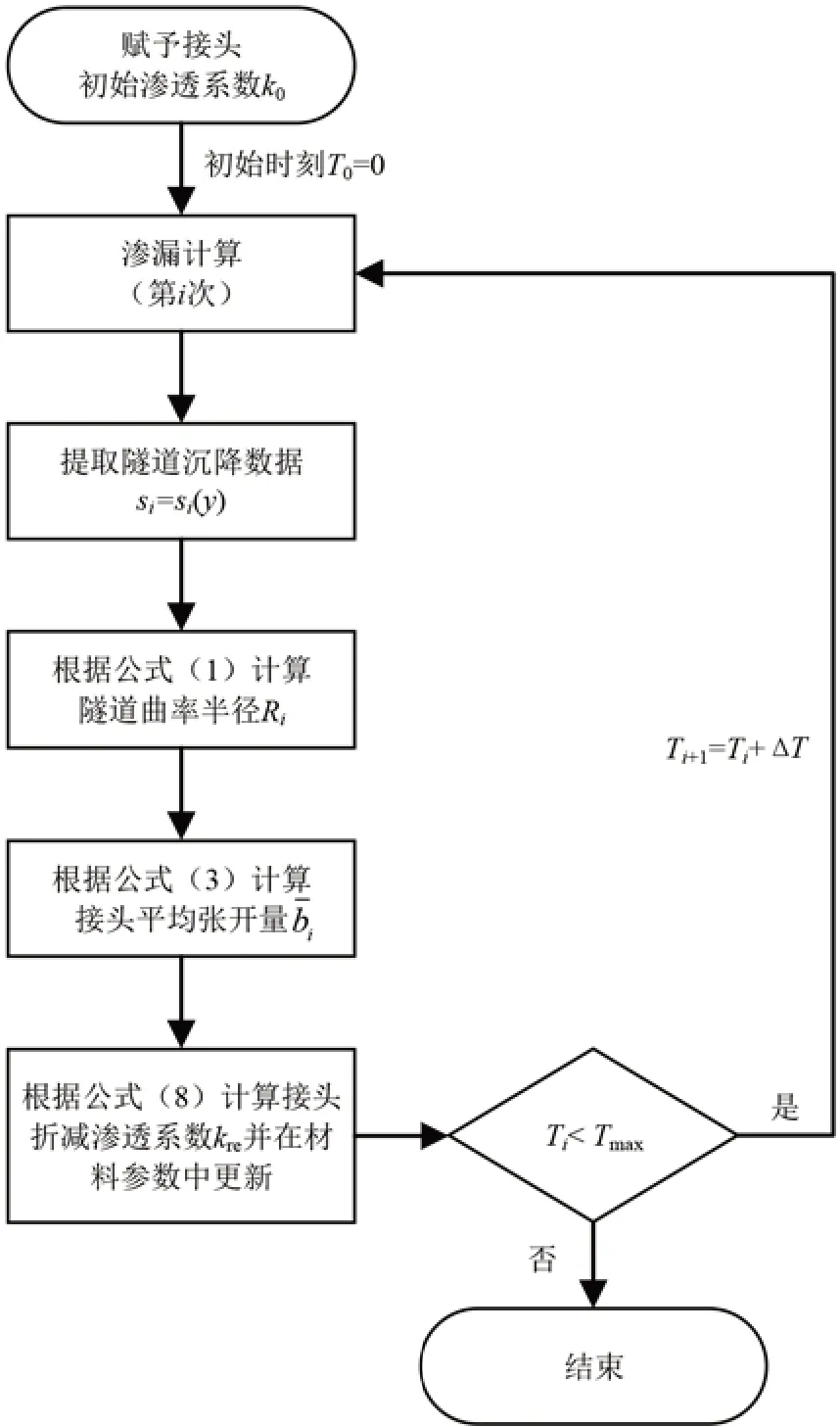
图4 渗透系数动态演化计算流程图Fig.4 Flow chart of dynamic evolution of permeability coefficient

2 数值模拟模型

本文以上海地铁1 号线为工程背景，选取典型地质剖面，利用通用有限元软件ABAQUS 建立三维模型进行数值模拟分析.隧道埋深在9～12 m，主要处在高压缩性、低强度、低渗透性的淤泥质黏土中，隧道下方存在深厚软土覆盖层.衬砌采用通缝拼接的形式，外径6.1 m，衬砌厚0.35 m，一环衬砌长1 m.

2.1 模型建立

模型的土层分布及计算参数参考Lee 等［20］以及Shen 等［21］的研究报道，具体参数如表1 所示，深度取50 m.

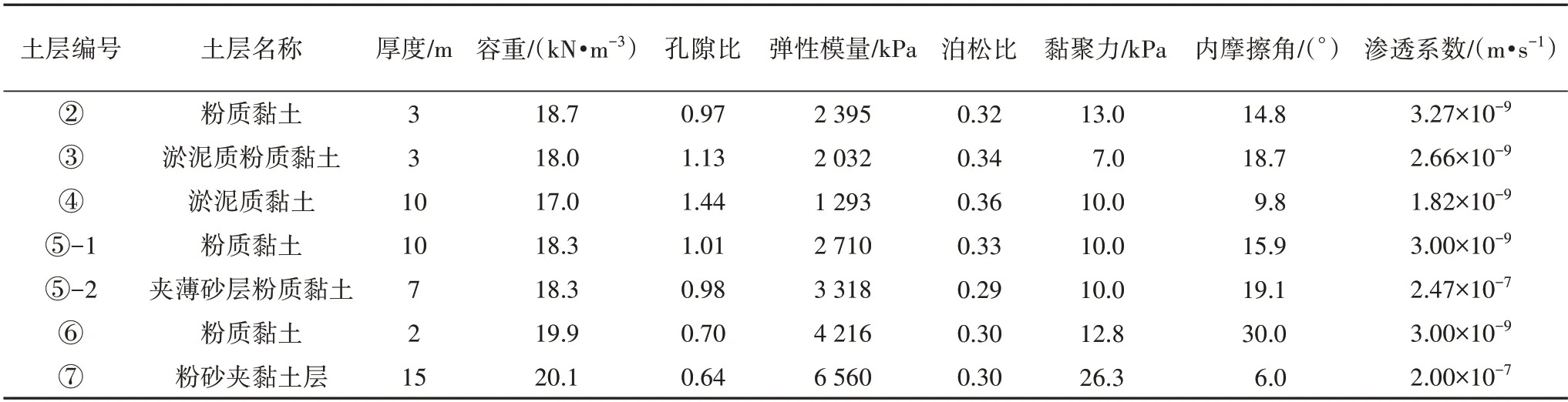
表1 土体计算参数Tabl.1 Calculation parameters of the soil

衬砌采用连续实体单元建模，在模拟衬砌的力学行为时，采用线弹性本构模型，隧道环缝接头降低了隧道的纵向刚度，黄宏伟等［22］以及李翔宇等［23］的研究均显示上海地铁1 号线盾构隧道的纵向刚度有效率约为0.1，因此将衬砌的弹性模量折减为3.45 GPa，容重取24 kN/m3.

在模拟衬砌的水力行为时，为了模拟真实的环缝接头渗漏情况，如图5 所示，本文在隧道中央划分出一环6 mm 宽的渗漏区域，赋予其不同的渗透系数表征其渗漏的强弱.

图5 单一环缝接头渗漏（灰色区域为渗漏区域）Fig.5 Single circumferential joint leakage（gray area refers to leakage area）

图6 展示了模型的网格划分.隧道埋深为11 m，渗漏接头的中心点O的坐标为（0，0，-11），Y方向上的厚度d为6 mm.土体与衬砌均采用实体单元建模，单元类型为C3D8P（八节点六面体单元，具有孔压自由度），可以进行流固耦合分析，整个模型共包括48 384 个计算单元，53 363 个节点，假设衬砌和洞周土体不发生相对位移，衬砌和土体在交界面共用节点.

图6 模型网格Fig.6 Model grid

2.2 计算步骤及边界条件

本文主要研究已建隧道接头渗漏对隧道以及周围环境的影响，因此并未模拟隧道开挖的过程.

计算步骤：①地应力平衡步——施加土体自重，获得模型初始应力状态，同时将初始位移归零.②渗漏步——设置渗漏边界，模拟隧道渗漏，进行长期固结分析.

边界条件设置如下：

①模型位移边界：四周边界约束水平位移，竖向位移自由；底部边界约束竖向以及水平位移；顶部边界水平和竖向位移自由.

②模型水力边界：四周的孔压保持初始静孔压不变，假定地下水稳定在地表，将地表的孔压设置为0.在地应力平衡步中认为隧道尚未渗漏，衬砌内侧流量设置为0，在渗漏步中认为衬砌内侧与大气连通，设置孔压为0，此时地下水可流入隧道内部.

2.3 渗漏模式

模拟隧道渗漏时，分别采用常渗透系数渗漏以及环缝接头渗透系数动态劣化两种模式进行模拟，渗透参数取值如下.

2.3.1 常渗透系数渗漏

该模式下，认为渗漏接头的渗透系数始终不变.环缝接头的渗透系数较难直接确定，本文根据渗漏量反演渗漏接头的渗透系数，《地铁设计规范》（GB 50157—2013）规定隧道全范围内的平均渗漏量的最大值为0.05 L/（m2•d），且任意100 m2范围，一昼夜的渗漏量不超过15 L，本文仅模拟了一环接头渗漏，并未研究全范围内的渗漏情况，因此采用15 L/d 的渗漏量控制标准，不发生渗漏区域的渗透系数按照混凝土防水标准取1.00×10-13m/s，反演得到渗漏接头的渗透系数为1.06×10-7m/s.

2.3.2 渗透系数动态劣化

该模式下，认为接头的初始渗透系数与常渗透系数反演值1.06×10-7m/s保持一致，随后按照图4 所示流程不断更新迭代，其中中性轴角度φ取0.963 5［17］.

在数值模拟中，渗漏的环缝接头宽度w定为6 mm，该区域在建模时就划分完成，在计算过程中无法任意修改.因此，不能直接将式（8）计算得到的渗透系数赋予渗漏接头.参考Davis 等［24］的研究，将渗漏区域的宽度从变为w，相应地，渗漏接头的渗透系数变为原来的倍，具体公式为

式中：keq为接头等效渗透系数；w为数值模型中环缝接头的宽度，本文中为6 mm；水的容重取9 800 N/m3；水的动力黏滞系数取1.01×10-3Pa·s.

设计要求隧道的使用年限不应低于100年，然而，通过试算发现在渗漏发生后的40年内，隧道以及土体的响应就会达到稳定状态，因此为节约计算资源，同时获得较为可靠的终值结果，将计算年限Tmax取80年.

3 计算结果与分析

3.1 地表沉降分析

3.1.1 对地表沉降终值的影响

地表沉降影响地面道路以及地上建筑物的结构性能，地表沉降的绝对值以及沉降范围是工程人员重点关注的指标.

图7 展示了环缝接头渗漏对地表沉降的影响，常渗透系数工况与渗透系数动态演化工况下，地表沉降的分布规律相似，在地表均会出现一个中心对称的“沉降漏斗”，渗漏中心对应的地表沉降值最大.考虑渗透系数动态演化得到的沉降值显著高于常渗透系数工况，常渗透系数工况计算得到的地表最大沉降为14.45 mm，考虑渗透系数演化计算得到的地表最大沉降为26.91 mm，比常渗透系数工况结果大86.23%.

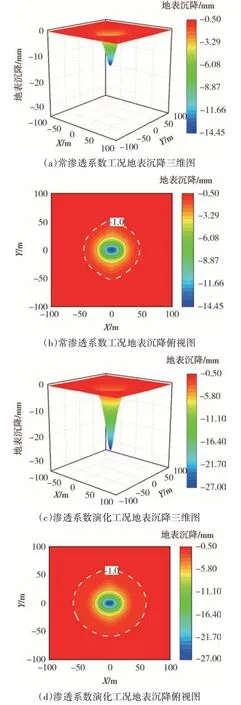
图7 地表沉降Fig.7 Surface settlement

为了定量表示地表沉降范围，以1 mm 为沉降阈值，沉降大于1 mm 的区域认为受到了接头渗漏的影响，在图7（b）、（d）中将沉降范围用白色虚线标记，可以看出，渗透系数演变工况下地表沉降范围显著高于常渗透系数工况.常渗透系数下，地表沉降在Y方向上从原点向外延伸52 m，X方向上向外延伸45 m，沉降面积为6 941 m2，考虑渗透系数演变后，地表沉降在X和Y方向上各延伸60 m，沉降面积为10 866.5 m2，范围扩大了56.56%.

Mair［5］在研究中指出伦敦某隧道渗漏后，距隧道100 m 处产生了可观测的地面沉降.本文数值结果显示一环接头渗漏时，地表沉降范围可延伸到距隧道60 m 处，如果渗漏接头数目增多，地表沉降范围会进一步增大.数值与实测结果都显示出隧道渗漏对地表的影响非常显著，综合地表沉降绝对值以及沉降范围来看，忽视了动态演化后，将显著低估隧道接头渗漏对地表沉降的影响.

3.1.2 地表沉降随时间的发展

了解地表沉降随时间的发展有助于选择隧道渗漏的控制时机，将地表最大沉降随时间的发展曲线绘制在图8 中.图中显示两种工况下地表沉降的发展趋势类似，渗漏发生初期，沉降发展极为迅速，随后发展速率减缓，在20年左右沉降趋于稳定.

图8 地表最大沉降的发展Fig.8 Development of maximum surface settlement

地表沉降的范围同样会随着渗漏的发生而逐渐增大，图9 展示了两种工况下地表沉降范围的演变情况，渗漏发生后的初期，地表沉降范围扩张较快，20 年后，沉降范围基本不扩张.考虑渗透系数演化后，最终的沉降面积为10 866 m2；渗漏发生后第1年，沉降面积就达到2 473 m2，占最终值的22.76%；渗漏发生后第10 年，沉降面积达到9 145 m2，占最终值的84.16%；渗漏发生后的第20 年，沉降面积达到10 496 m2，占最终值的96.59%.

图9 地表沉降范围的发展Fig.9 Development of surface settlement range

综合地表沉降值以及沉降面积随时间的变化情况，环缝接头渗漏时，考虑渗透系数动态演化后，地表沉降值以及地表沉降范围显著增加，而地表沉降的发展趋势受到的影响较小，两种工况下，地表沉降在渗漏发生后的20 年基本达到稳定状态.在渗漏发展后的初期，是地表沉降值以及沉降范围发展最快的阶段，也是渗漏治理的黄金时期.

3.2 隧道纵向变形

3.2.1 对隧道沉降终值的影响

在实际工程中，隧道常常因为纵向不均匀沉降而导致接头张开以及管片开裂［25］.因此，研究隧道的纵向不均匀变形至关重要.图10 展示了隧道的纵向不均匀沉降，横坐标Y为隧道纵向上的距离，渗漏中心（Y=0）处的隧道沉降值最大，常渗透系数下，隧道最大沉降为5.68 mm，考虑渗透系数动态演化后，隧道最大沉降为10.43 mm，沉降量增大了83.63%.此外，渗透系数演化下的隧道沉降曲线更为陡峭，意味着此时的纵向曲率半径更大.隧道允许的曲率半径为15 km，常渗透系数下，隧道的曲率半径为18.69 km，并未超限，而考虑渗透系数演化后，稳态的曲率半径为9.74 km，相比于常渗透系数减小了47.89%，已超过限制值，将对地铁的运行安全造成重大威胁.

图10 隧道纵向沉降Fig.10 Longitudinal settlement of tunnel

相关运营单位对上海地铁隧道的沉降进行了长期的监测，积累了宝贵的数据.郑永来等［17］采用三次多项式曲线对上海地铁1 号线的隧道沉降进行分段拟合，统计了某区间的曲率半径分布情况，发现高达10%的区域隧道曲率半径小于15 km，在最严重的区域，曲率半径甚至达到了684 m.本文计算出在一环接头渗漏时，最严重的情况下，曲率半径可以达到9.74 km，这是因为隧道渗漏虽然会引起隧道纵向不均匀沉降，但并非唯一原因.本文的数值模拟假设土层分布均匀，实际情况下隧道往往会穿越不同性质的土层.叶耀东［26］曾对不同下卧层的隧道工后沉降进行研究，发现下卧软土层的模量越大，厚度越小，则工后沉降越小.隧道跨越的土层差异越大，则纵向沉降越不均匀.此外，地面超载、注浆不均匀、邻近施工活动均会加剧隧道的纵向不均匀沉降.在多种因素的综合作用下，隧道的实际曲率半径可以到极小的程度.隧道渗漏虽然只是诱发纵向不均匀沉降的原因之一，但是曲率半径依然存在超限的可能性，因此对渗漏问题仍旧要高度重视，及时处理.

3.2.2 隧道沉降随时间的发展

为了研究隧道沉降的发展规律，提取了不同时间的隧道沉降曲线，绘制在图11 中，T为渗漏发生后的时间.图11 显示，随着渗漏的发展，隧道的沉降值、沉降范围都会逐渐增大，渗漏发生后的初期，沉降发展较快，渗漏发生后17.3 年与80 年的曲线基本重合，代表此时沉降已基本稳定.常渗透系数与渗透系数演化工况下隧道沉降的发展规律类似，在此不另展示.

图11 渗透系数演化工况下隧道纵向沉降的发展Fig.11 Development of longitudinal settlement of tunnel under the condition of permeability coefficient evolution

图11 中，距离渗漏接头较远的区域沉降发展较慢，而渗漏接头附近的区域沉降发展迅速，这就导致沉降曲线更为陡峭，即隧道的曲率半径随渗漏的发生而逐渐减小.将Y=0 处隧道曲率半径随时间的发展绘制在图12 中，可以看出，曲率半径在渗漏发生后迅速减小，1 年后趋于稳定状态.考虑渗透系数演化后，渗漏发生后的0.2 年，曲率半径就超过了临界值15 km.为了保证隧道的结构安全，对于隧道病害的治理，应该在渗漏发生后的0.2年内完成.

图12 隧道曲率半径的发展Fig.12 Development of tunnel curvature radius

3.2.3 对接头张开量的影响

得到了曲率半径随时间的发展趋势后，可以根据公式（1）计算得到环缝接头的最大张开量δj随时间的发展情况，将结果绘制在图13 中.接头张开量与曲率半径呈反比，因此变化趋势与曲率半径相反.常渗透系数下，计算得到最终的接头最大张开量为0.28 mm，而一旦考虑管片的循环劣化、渗透系数动态演化后，接头的张开量在渗漏发生初期迅速增大，最终稳定在0.53 mm，相较于不考虑渗透系数动态演化的情况，增幅达到了89.29%.虽然接头的张开量较小，但若因此就忽视接头张开的话，则会引起严重后果.接头张开不仅会导致地下水渗入隧道内部，严重情况下，甚至会导致漏泥漏砂灾害，影响隧道周围土体的稳定性，造成隧道失稳破坏［6］.此外接头张开会使得止水密封垫暴露在外部环境中，加速密封垫的老化，缩短使用寿命，影响结构的耐久性.因此，对于管片的张开问题，要引起足够的重视，忽略渗透系数演化，将会显著低估接头的张开量，使得工程人员轻视隧道渗漏造成的危害.

图13 接头最大张开量的发展Fig.13 Development of maximum joint opening

3.2.4 对衬砌变形的影响

渗漏发生后，衬砌发生了相应的变形，图14 展示了衬砌竖直方向以及水平方向上直径的变化量ΔDv、ΔDh（以直径增大为正，减小为负）.图14 显示，在隧道发生环缝接头渗漏时，衬砌竖直方向的直径减小，水平方向上的直径增大，衬砌将从圆形趋于扁平化.在变形的量值上，渗漏接头处的变形最显著，远离渗漏接头，变形量逐渐减小.考虑渗透系数演化后变形量显著高于不考虑渗透系数演化的工况.常渗透系数下，衬砌竖向直径最大减小0.71 mm，水平直径最大增大0.62 mm；考虑渗透系数演化后，竖向直径最大减小1.19 mm，水平直径最大增大1.13 mm.数值结果显示，衬砌水平向的变形略微小于竖直向的变形，但是总体上看，变形量很小，均远小于设计标准0.5%D（D为衬砌外径）.

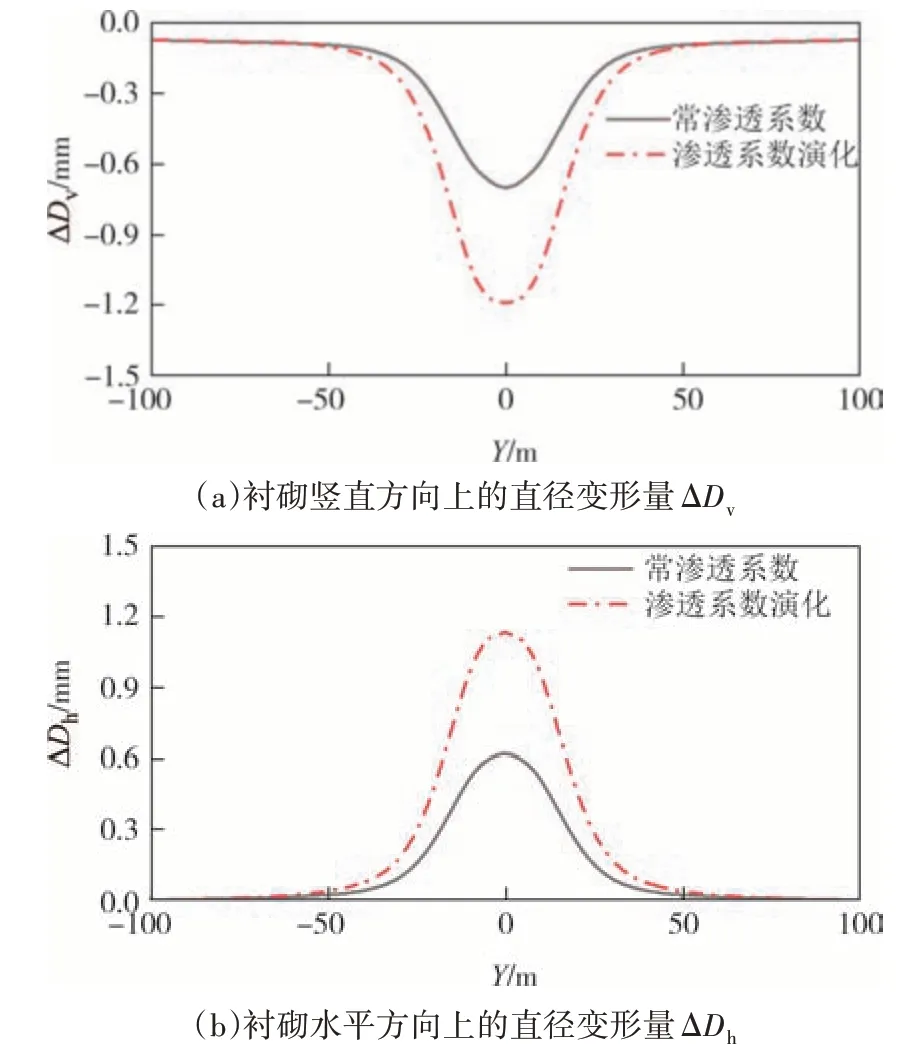
图14 衬砌直径变形Fig.14 Deformation of lining diameter

3.3 止水能力影响

由于环缝接头处的止水密封垫具有膨胀性，因此接头处渗透系数在环缝张开初期增长较慢，后期逐渐加快.在式（7）的基础上引入指数n描述接头渗透性折减系数随环缝张开的非线性变化：

令式（10）中指数n分别为1.0、1.5、2.0、2.5、3.0进行对比分析，其中n=1.0 时即为折减系数线性变化.图15 是隧道曲率半径随时间发展曲线，可以发现考虑折减系数非线性变化后，渗漏初期隧道曲率半径变化速率减小，但对稳定后的最终结果影响不大.渗漏发生约17 年后，曲率半径发展基本稳定且最终结果较为接近.

图15 曲率半径随时间变化Fig.15 Development of tunnel curvature radius

选取地表最大沉降、地表沉降范围以及隧道最大沉降进行分析，见图16.当n小于或等于2.5 时，在沉降发展过程中的结果较为接近，非线性影响不明显；而n为3 时，各沉降指标随时间的发展显著慢于其他情况.

图16 折减系数非线性影响结果Fig.16 Non-linear effects of the discount factor

随着指数n的变大，前期折减系数增长更慢，后期发展更快，最终都会趋于1.相应地，接头渗透性也在环缝张开初期较弱，后期显著增强并且趋于一致.渗漏稳定后的结果由接头在环缝张开后期的渗透性决定，因此各指标稳态结果相近.指数n的取值反映了环缝接头的止水性能，其对最终沉降结果影响较小，但良好的止水措施能显著减缓各沉降指标随时间的发展，为保障隧道安全运行，开展渗漏治理赢得时间.

4 结论

1）本文提出的渗透系数演化方法反映了“隧道变形―接头张开―渗漏加剧”这一循环劣化过程，这是以往常渗透系数假设无法考虑的.常渗透系数假设显著低估了隧道渗漏的危害程度，应该采用更符合实际的渗透系数动态演化模型对隧道渗漏问题进行研究.

2）渗漏接头附近土体变形最明显，远离接头，变形程度小.地表沉降在渗漏中心最大，远处地表沉降小，地面沉降呈现“漏斗”状；隧道沉降在渗漏接头处最大，远处沉降小，隧道在纵向呈不均匀沉降，导致接头逐渐张开，衬砌出现扁平化变形，但是总体变形量很小，不会超出安全控制标准.

3）本文工况下，地表沉降、隧道沉降在渗漏发生20年后基本达到稳定状态，渗漏发生后的初期，是沉降发展最快的阶段，同时也是渗漏治理的黄金时期.曲率半径以及接头张开量在渗漏发生1 年后就趋于稳定，考虑渗透系数动态演化后，环缝接头渗漏发生0.2 年后，隧道的纵向曲率半径就超出安全控制标准.因此为了保障隧道运营的安全，同时控制沉降的发展，建议对饱和软土地区隧道渗漏的治理在0.2年内完成.