基于改进BP 算法的岩石宏细观参数轻量化分析方法

任俊卿 ，肖明 †，刘国庆

（1.武汉大学 水资源工程与调度全国重点实验室，湖北 武汉 430072；2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100048）

岩石是一种复杂的矿物集合材料，普遍包含节理、裂隙等原生结构面，甚至有断层穿过［1］.表现出复杂的非连续、非均质、各向异性等非线性特征.其力学特性和损伤演化机理对岩土工程的损伤破坏与防灾减灾研究具有重要的理论意义与工程价值.与连续介质数值方法相比，PFC（Particle Flow Code，颗粒流程序）能够合理模拟岩土大变形，可在细观尺度再现岩石中裂纹的萌生、扩展及汇合过程，是研究岩石损伤与破坏机理的有效数值手段和重要理论突破.

选择合理可靠的输入参数是准确进行数值模拟的前提，因此PFC 细观参数标定问题一直以来都是岩土工程数值模拟中的热点与难点，大量的细观参数使得其成为复杂的高维非线性问题，导致计算成本过高，模型可解释性不足等缺陷，限制了PFC 数值模拟方法的应用与发展.因此在研究时对冗余的细观变量进行合理剔除，化繁为简，寻找一种精度高、变量少且易于计算和解释的轻量化分析方法并应用于PFC参数标定问题中尤为重要.

宏细观参数间的相关关系与内在关联是PFC 标定研究的基础［2］.赵国彦等［3］和Chen［4］应用理论和数值方法研究了PFC 不同接触模型宏细观参数间的相关关系，建立了两种尺度参数间的半定量函数模型，提升了传统试错法的标定效率；张国凯［5］等、Shi等［6］研究了簇颗粒几何特征及裂纹分布对岩石宏观力学行为的影响；丛宇［7］等、阿比尔的等［8］较全面的探索了岩土材料宏细观参数的相关性，考虑了细观参数对岩石的剪切力学行为的影响.

在宏细观参数标定方法方面，目前主要有基于优化技术、数据挖掘、机器学习等技术的方法，如杨文剑等［9］提出了碎石类材料的细观参数标定方法.Yoon［10］和邓树新等［11］采用中心复合试验设计和优化技术相结合的方法获得了岩石材料宏细观参数间的定量关系，该方法对多种岩石（硬岩、软岩）均有良好的标定效果；Zou 等［12］以煤为研究对象，基于灰色关联分析、响应面法和马氏距离测量法提出了一种组合优化标定方法；Xu 等［13］将迭代思想引入参数标定中，显著提升了标定的效率和准确性；此外，周小棚等［14］利用数据挖掘、神经网络等方法对材料细观参数进行了初步预测.

综上所述，岩土体宏细观参数间的响应规律是颗粒离散元数值研究中一个重要的研究方向，目前国内外采用理论分析、室内试验和数值模拟等方式在该方面取得了一定成果，但仍有以下几个方面值得进一步研究探讨：1）现有研究倾向于全面分析所有细观参数对宏观参数的影响，模型冗余度高且分析耗时，难以揭示宏细观参数间的影响机制，往往效果不佳.2）多数研究成果是基于PFC 2D 和室内双轴试验获得的，然而在实际工程中，岩石处于三向复杂应力状态，并非所有的岩石材料都能够简化为平面问题，因此该方法具有一定的局限性.

针对以上问题，本文在众多学者研究成果的基础上，以获得三维条件下高精度、低维度、易分析解释的宏细观参数模型为目标，首先通过正交设计和三轴数值试验获得一定的研究样本；然后基于改进的BP 算法进行轻量化处理，准确量化各细观参数对宏观参数的影响程度，筛选出对宏观参数有显著影响的关键细观参数，对于影响不大的细观参数则进行剔除，由此获得简单且易于分析的宏细观参数模型，即轻量化模型；最后针对轻量化模型分析了宏细观参数间的相互作用规律及影响机制，希望对PFC细观参数标定问题提供一定依据.

1 PFC接触模型选择

岩石是由矿物颗粒和胶结物组成的复杂混合体，通常采用平行黏结模型来表征其接触行为，该模型通常分为线性和黏结两部分，分别用于描述矿物颗粒之间的接触行为及胶结物质.平行黏结模型的接触示意图和接触模型见图1.

由图1 可见，模型的线性元件和平行黏结元件平行作用，并在两个接触部件之间建立弹性相互作用.模型具有轴向、切向及旋转刚度.除此之外，通过引入阻尼项完成模型的能量耗散过程.平行黏结模型颗粒受力与破坏机制如图2所示.

对于线性接触部分，当两颗粒间的剪切接触力超过允许最大剪切接触力时，颗粒间将发生滑移.黏结部分的强度准则可按梁弯曲理论描述，即颗粒间的最大法向或切向应力超过其许用应力时，黏结发生破坏，并随即产生一个张拉裂纹或剪切裂纹.

2 细观参数及试验方案设计

2.1 宏细观参数定性关系描述

2.2 正交试验方案

本文是对平行黏结模型的细观参数进行轻量化研究，首先对模型的几何尺寸、颗粒密度、孔隙率进行固定，按水利水电岩石试验规程对试件尺寸的规定，数值试验采用底面半径50 mm、高100 mm 的圆柱体试样；Nohut 等［15］的研究表明，密度对标定结果影响甚微，因此参照岩石的宏观密度取2 700kg/m3；孔隙率按文献［3，8，16］建议取0.16.

由于参数较多，交叉及不确定性较大，常规试验方案需要大量试验次数及计算资源.正交试验能够综合考虑各因素间的交叉作用，在结果可靠的前提下有效减少试验次数.按照正交设计原理，本文设计了一个L50510型正交表（10 因素5 水平50 次试验）进行三轴压缩数值试验，具体方案见表1.

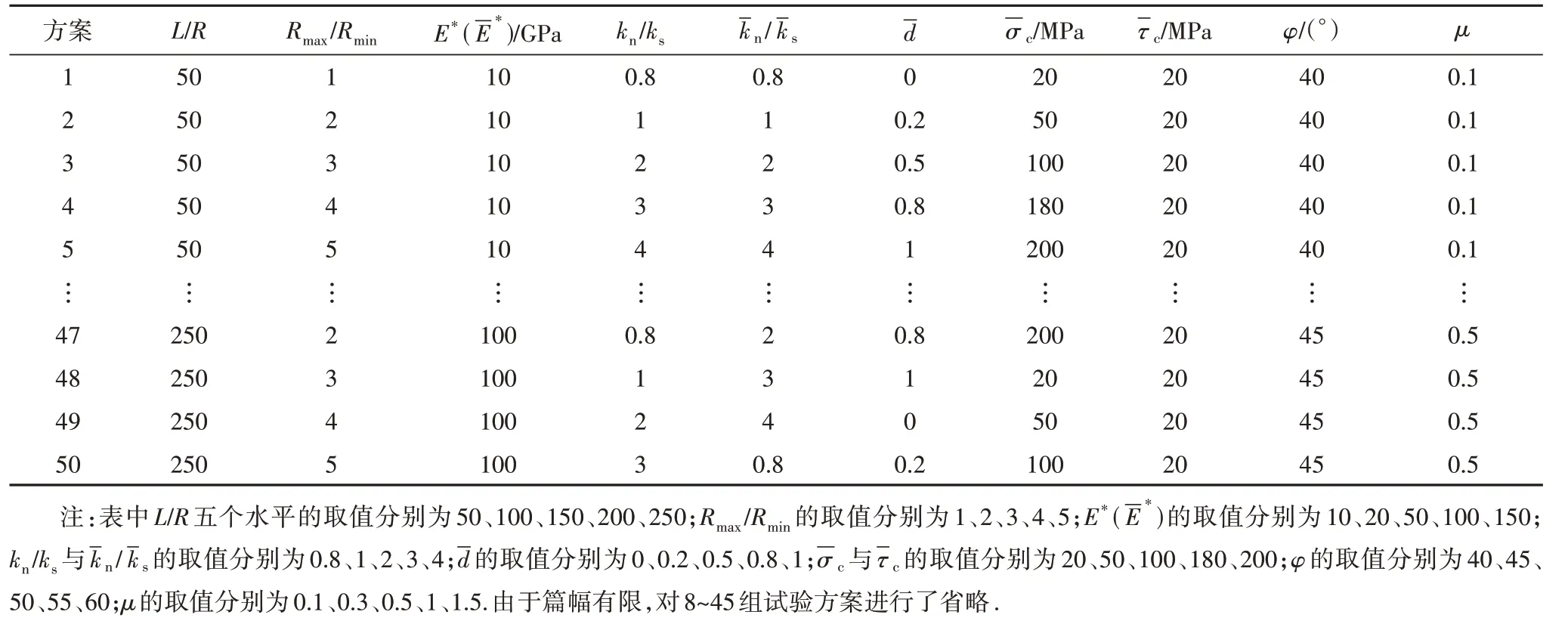
表1 正交试验方案Tab.1 Scheme of orthogonal test

为消除各细观间量值大小差异对研究带来的不利影响，提高结果的准确性与可靠性，首先对细观参数进行如下标准化变换：

变换后新的参数序列均服从标准正态分布，yi～N（0，1），便于各参数间进行分析与比较.

2.3 数值试验及伺服加载

本文采用PFC 3D 模拟岩石三轴压缩试验，模型如图3 所示.数值试验中保持恒定的细观参数按表2选取，围压设置为10 MPa.

表2 模型公共细观参数Tab.2 Basic mesoscopic parameters in model

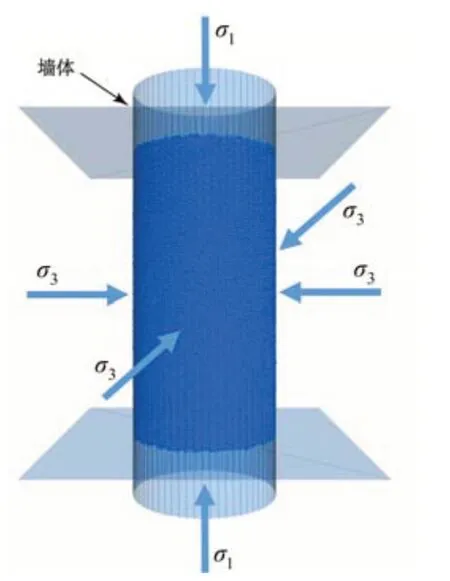
图3 三轴压缩数值模型Fig.3 Numerical model for triaxial compression test

三轴试验模型的加载通过对墙体施加固定速度实现，但每个颗粒的应力状态在每时每刻都会更新，静态加载方式会因颗粒之间及颗粒与墙体之间的相互作用导致三个方向的应力量值很难维持恒定.为提供一个稳定的围压，需对墙体进行伺服控制［18］.伺服过程中边界墙体的速度按下式确定：

式中：G为伺服系数；σmea为当前应力；σreq为目标应力.

式中：m为接触个数；A为接触面积；β为保证迭代稳定的控制系数，取0～1之间的值.

3 基于改进BP算法的轻量化建模方法

大多学者的研究表明，材料宏细观参数之间关系密切，细观参数不仅独立地对宏观参数产生影响，各参数之间往往还存在一定的交叉及关联作用，使得PFC 宏细观参数分析及标定成为典型的高维问题.如果不加处理将所有参数考虑在内，虽在一定程度上增大了精度，但也使得标定的难度和计算成本大幅增加，甚至使得模型的可解释性受到影响.因此对模型进行轻量化处理，合理筛选出关键变量并剔除冗余数据对准确高效标定至关重要.

BP 神经网络是处理非线性问题的有力工具，也是机器学习中最流行的智能算法之一.通过其强大的学习、并行和容错能力，可以准确、高效地实现从输入层到输出层的非线性映射.它广泛应用于非线性系统、函数逼近、系统辨识等领域，可以解决岩土工程领域的参数标定、预测、反演、建模等复杂工程技术问题.

本文提出了一种改进的BP 算法，在计算中能灵活变换功能函数形态、自适应调节动量系数和学习率，弥补了常规算法精度低、稳定性不佳，收敛缓慢等不足.在对正交试验结果进行训练后可对宏细观参数间的相互影响程度进行排序，筛选出关键的细观参数，达到降低模型维度和轻量化目的.

3.1 BP算法基本原理

不同于统计学模型，神经网络不需要试验样本满足正态分布、方差齐性、样本数量趋于无穷大等条件，通过其较强的学习、并行与容错能力，可准确高效地实现从输入层至输出层的非线性映射［18］.

基于BP 算法的多层感知器神经网络是一种典型的前馈型神经网络，一般由三部分构成，如图4 所示，一组由源节点组成的输入层，由计算结点组成的若干隐含层及输出层.BP 算法求解的基本原理可以概括为输入信号的正向传播与误差的反向传播两个过程，通过周而复始地交替迭代直至模型误差最小.

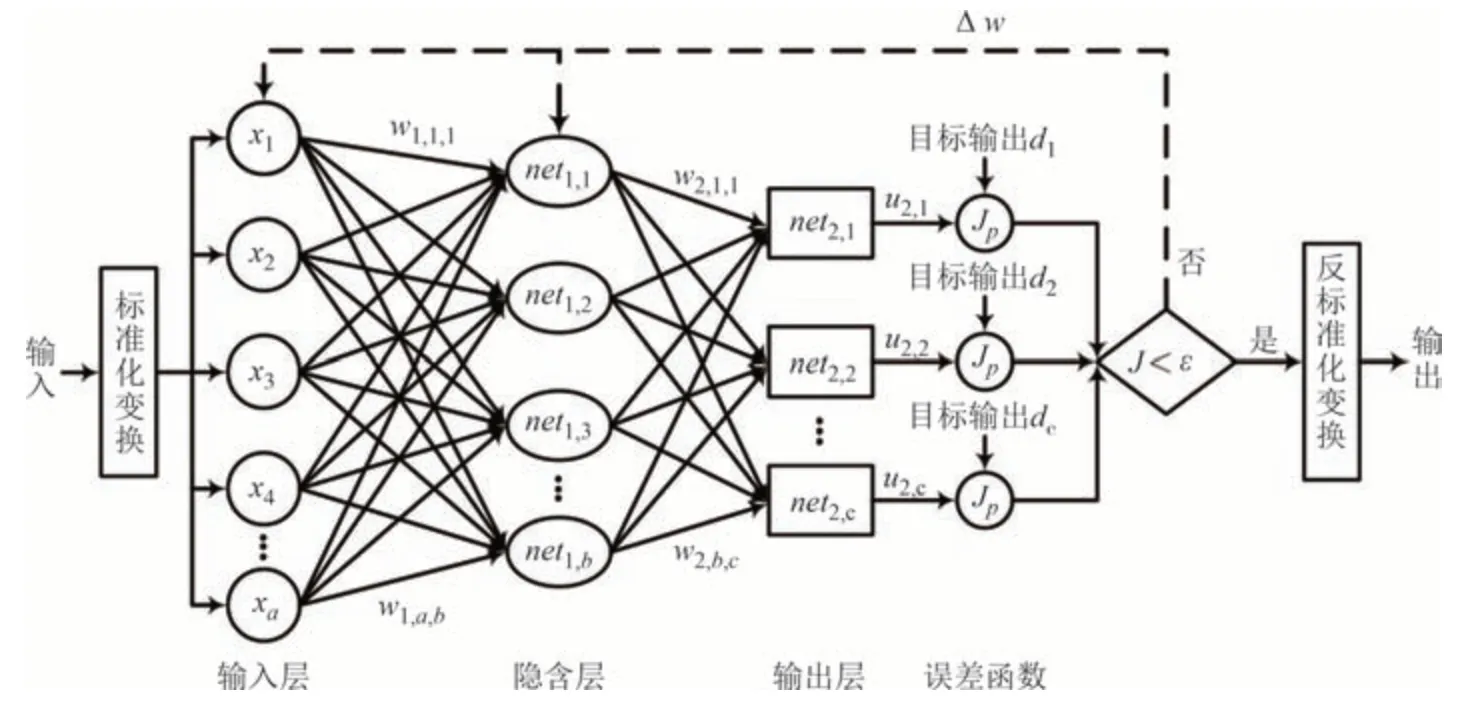
图4 BP神经网络的拓扑结构与信号流向Fig.4 Topological structure and signal flow direction of BP neural network

采用Sigmoid 函数作为神经元功能函数，用于建立输入（细观参数）输出（宏观参数）间的映射关系：

当网络的实际输出和目标输出（室内试验测得的宏观参数）不等时，即存在误差，定义误差函数：

式中：Jp为第p个样本误差函数；L为网络层数.

以误差函数为目标函数，采用梯度下降法对网络各层权值进行迭代修正：

式中：η为学习率，η∈(0，1).

对隐含层则有递推公式：

由权值修正公式（8）可知，权值的修正过程即为误差信号由输出层向输入层的反向传播过程，当误差达到给定精度后，训练终止.

传统BP 算法简单易用，具有较强的非线性映射能力和泛化能力，但该算法在实际应用中也存在固有缺陷，如容易陷入局部极小值、收敛速度慢、学习率不可调、学习记忆时间短等［19］.因此本文针对以上缺陷，对传统BP 算法进行适当优化改进，旨在提升算法的精度、计算效率与稳定性.

3.2 改进的BP算法

3.2.1 功能函数中引入陡度因子

Sigmoid 函数的图像为S 型曲线，在定义域的两端各存在一段饱和区，在饱和区内，节点输出对权值的修正量变化并不敏感，如果此时网络的误差依然很大，那么很难在短时间内通过权值的修正而降低误差，即进入了误差曲面的平坦区［20］，网络的收敛速度将会受到很大影响.因此可以向Sigmoid 函数中引入一项陡度因子［21］δ，即

陡度因子在训练前一般初始化为1，若训练过程中发现网络误差变化量很小但误差值较大时，可认为进入了误差曲面的平坦区，此时应适当增大δ，对功能函数的形状加以变化，增大非饱和区的范围，当退出平坦区后，将δ恢复初值.改进后可使网络的迭代次数明显减小，提升训练效率.

3.2.2 引入自适应动量项

由式（7）可知，传统BP 算法在权值迭代中只考虑当前误差曲面的梯度方向，忽略了之前的梯度方向，使训练过程出现震荡效应，收敛缓慢且易陷入局部最优.因此在式（7）基础上引入动量项，将权值的修正量由上次权值的修改方向和本次误差曲面的梯度方向共同决定.动量项反映了前期权值调整积累的经验，对本次修正起阻尼作用.当误差曲面起伏较大时，可有效减小震荡，加速收敛.本文在经典动量方法的基础上，采用Nesterov 动量方法［22］对网络权值进行迭代，其中经典动量方法为：

式中：α为动量系数，α∈［0，1）.

Nesterov动量方法可按下式表达：

对比以上两式可以发现，相比与经典动量方法，Nesterov 动量的梯度计算在当前速度之后，因此可以看做是在经典动量中添加了一项校正因子.

下面讨论动量系数的取值问题，一般来说，动量系数常按研究者的经验选取，如赵林明等［23］认为动量系数在0.9～0.98 之间网络的收敛速度较快，不同学者的选取策略常导致不同的训练效果，在实际应用中动量系数取的过小会降低网络的收敛速度，过大则会导致发散，并且固定的动量系数难以适应复杂误差曲面的形状变化，本文则依据误差曲面的梯度和误差函数的调整方向计算出自适应变化的动量系数，提高网络的训练速度和稳定性：

3.2.3 自适应学习率

学习率是BP 算法中一项至关重要的超参数，其取值将直接影响到网络的训练性能，关系到模型的收敛速度及精度，一般也是按经验取为一固定常数，但在实际应用中，很难给出一个从始至终都最优的学习率［24］，因此变学习率算法在模型训练中将体现出巨大优势.在开始阶段或误差曲面的平坦区，应选取较大的学习率，加快训练速度的同时避免陷入局部最优；训练至后期或在误差曲面陡峭部位，过大的学习率则会导致振荡效应，难以收敛.本文针对此问题提出一个按照误差曲面梯度和迭代次数自适应调节学习率的计算方法：

式中：d为迭代次数；dmax为最大迭代次数；λ为经验系数.

由式（13）可知，自适应学习率可以灵活地调节迭代步长，相比于固定学习率算法，改进算法在训练速度、准确率和稳定性方面均有所提升.

基于改进BP 算法的细观参数轻量化建模流程如图5 所示，采用不同自变量值测量网络模型预测值的变化量来衡量各变量的重要性，从而实现每个变量的重要性输出.对重要性值低的细观参数进行合理剔除，从而使分析模型简洁、轻量.

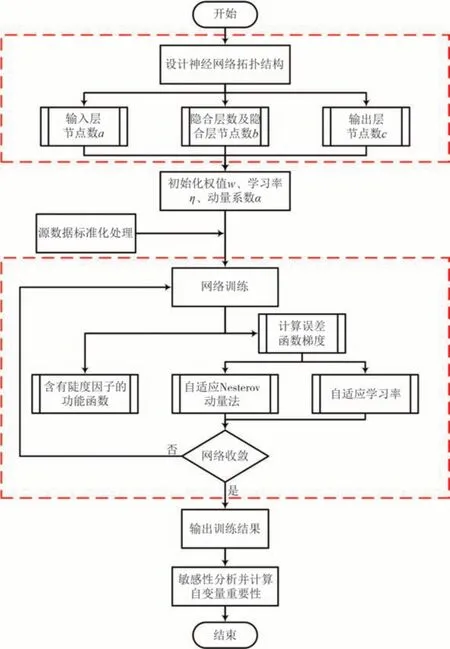
图5 基于改进BP算法的细观参数轻量化建模流程图Fig.5 Flow chart of meso parameter lightweight modeling based on improved BP algorithm

3.3 轻量化分析结果

采用单合隐层神经网络结构，分别利用传统BP和改进BP 算法进行宏细观参数轻量化分析.训练时动量系数的初值均取0.9，学习率为0.05.图6 为训练得出的轻量化分析结果，由图6 可见，两种分析方法得出的结论基本一致，互相印证了分析计算结果的正确性，说明具有全局搜索能力的BP 算法能够应用于宏细观参数的轻量化分析.

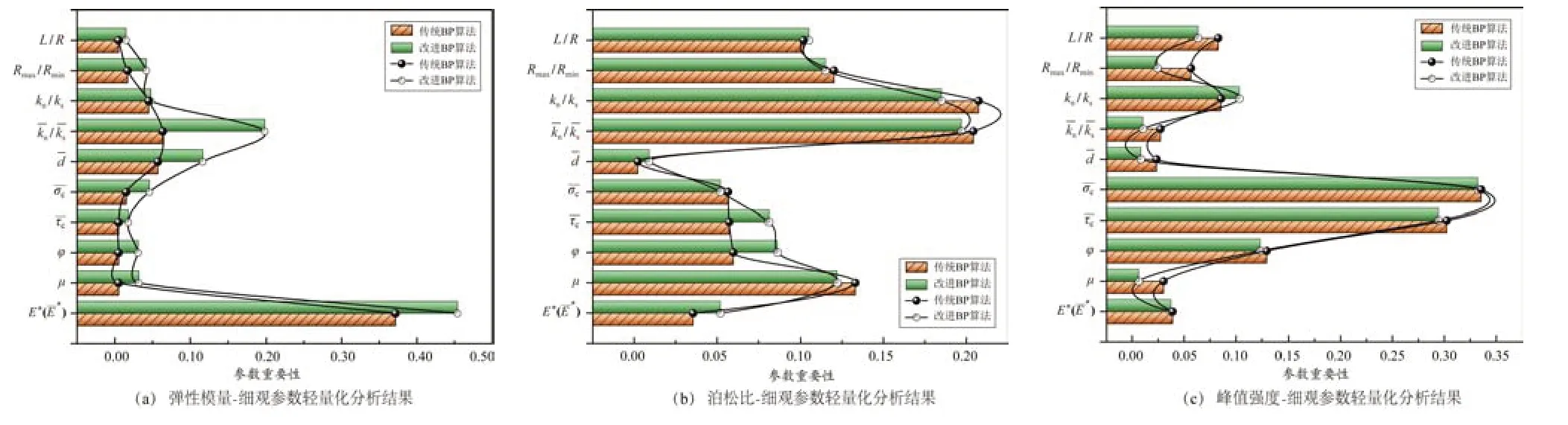
图6 宏细观参数轻量化分析结果Fig.6 Results of lightweight analysis between macro and meso parameters

图7 为两种算法进行轻量化分析时的迭代收敛曲线.由图可知，改进BP 算法在对弹性模量、泊松比和峰值强度轻量化分析时的训练效果均明显优于传统算法，训练精度高、收敛速度快，训练过程稳定.以弹性模量的轻量化过程为例，迭代50 次左右后可收敛于误差值0.01附近.而传统BP算法在前15次迭代中误差下降速度较快，但迭代至15～60 次左右时，网络的收敛速度明显变慢，并且有两次陷入局部最优值，经过多次迭代才得以跳出.迭代次数大于60 后，误差开始缓慢减小并趋于收敛，但收敛过程中网络震荡幅度较大，迭代至80～120次时震荡幅度可达22%，继续迭代至160 次后伴随小幅震荡并收敛于误差值0.019附近，与本文方法相比，误差增大了47%左右.

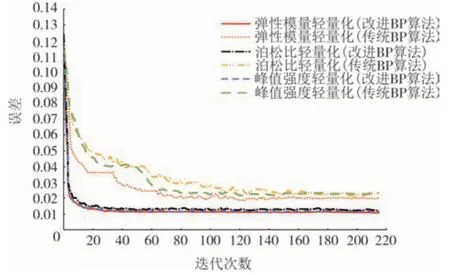
图7 宏细观参数轻量化分析的迭代收敛曲线Fig.7 Iterative convergence curve for lightweight analysis between macro and meso parameters

综上对比可见，本文方法在BP 算法的功能函数和权值修正和迭代策略方面进行了改进，使得改进BP 算法在计算精度、收敛速度和稳定性方面均明显高于传统方法.从机理上讲，自适应动量和学习率可以根据不同的误差曲面，实时调整权值修正策略及迭代方法，避免了搜索中陷入局部最优及震荡效应，使迭代曲线更加平滑.引入陡度因子的功能函数能够使迭代快速跳出平坦区，有效减少迭代次数.从本质上讲，在误差曲面上不同的搜索路径使得改进算法在迭代40～50 次左右后就可稳定收敛于误差值0.01，准确性更高，速度更快，获得的轻量化结果更加可靠且便于操作，在宏细观参数轻量化分析中具有一定优势.

由此可见，通过轻量化分析，对每个宏观参数均筛选出了3 个影响最为显著的细观参数，其余变量则进行合理剔除，将原有的10 个变量非线性关系简化至3 个，大幅节约了计算成本，为后续研究提供了便利.

综上所述，通过引入含陡度因子的功能函数、自适应Nesterov动量法及自适应学习率改进的BP算法提升了传统算法的稳定性与收敛速度，有效降低了模型维度，合理地简化了宏细观参数分析模型，达到了轻量化目的，为准确进行宏细观参数影响特性分析及参数标定奠定了基础.

4 宏细观参数相关性及影响特性分析

4.1 单一细观参数对宏观参数的影响特性分析

根据上文轻量化分析结果，将筛选出的有显著影响的细观参数做进一步研究，获得了宏细观参数间的箱线变化趋势图（图8）.图8 中每个箱线的上、下边缘分别表示同一水平数据中除异常值外的最大、最小值；中间箱盒的底部为下四分位数；顶部为上四分位数；中部红线为中位数；小圆圈则表示异常值，异常值的判定为高于数据的上限或低于下限，上、下限是由对应的四分位数和四分位距（上、下四分位数的差值）计算得来，下限值为下四分位数和1.5 倍的四分位距之差，上限值则为上四分位数和1.5倍的四分位距之和.

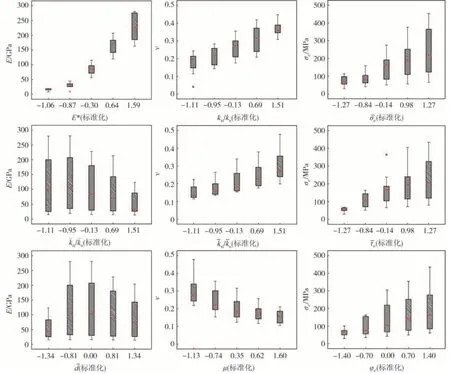
图8 宏细观参数箱线变化趋势图Fig.8 Boxplot between macro and meso parameters

4.1.1 细观参数对宏观弹性模量的影响

由图8 可见，随着等效模量的增加，弹模整体呈增加趋势.这种增加可以分为两个阶段，当等效模量较小时，增加幅度不明显，大于20 GPa后开始显著增长，其中位数基本呈线性增长.每个箱盒分别来看，可知同一水平下的宏观弹模近似呈正态分布，等效模量较低时，其四分位距较小，随着等效模量的增加，宏观弹模的分布也逐渐离散化.

在平行黏结刚度比方面，随着刚度比增加，弹模呈非线性减小趋势.当时这种趋势基本可以线性化.每个箱盒分别来看，同一水平下弹模的分布均比较离散，呈右偏分布.总的来看，弹模随刚度比减小的速率要小于随等效模量增加的速率，可见等效模量是影响宏观弹模最重要的因素.这与轻量化分析所得的结论是一致的.

4.1.2 细观参数对泊松比的影响

随着摩擦系数增加，泊松比基本呈二次曲线的减小规律.本文的研究表明，μ对于弹模和峰值强度两个宏观参数具有正向激励作用.摩擦系数较小时，泊松比减小幅度较大；当μ>0.5 后减小趋势逐渐平缓，量值基本在0.2～0.3 左右波动，这也是工程中常见岩体材料泊松比的取值范围，建议在对摩擦系数进行参数标定时可取0.5作为初始值.

4.1.3 细观参数对峰值强度的影响

在平行黏结抗剪强度方面，峰值强度呈现增长率逐渐减小的抛物线变化规律在50～100 MPa 区间段峰值强度增长最为明显，之后其中位数及第一四分位数变化曲线逐渐平缓，第三四分位数及上限值还有所增长.在数据分布方面，规律和基本类似，在此不再赘述.

峰值强度随内摩擦角增加基本呈线性增长，同一水平下峰值强度呈右偏分布，内摩擦角越大，数据波动范围也相应增大.同时，内摩擦角对岩石峰后强度具有一定影响，这是由于峰后加载时，内摩擦角对剪切带两侧的颗粒滑动具有一定控制作用.

4.2 多个细观参数对宏观参数的影响特性分析

前述章节对宏细观参数之间变化规律进行了初步分析，通常来讲，宏观参数往往受多个细观参数共同影响，单一参数很难对某个宏观参数起到决定性作用，这也解释了箱线图中四分位距较大的原因.因此本节将上文筛选出的细观参数进行交叉组合，研究多细观参数影响下宏观参数的变化规律.

4.2.1 多个细观参数对弹性模量的影响

4.2.2 多个细观参数对泊松比的影响

由前文分析可知，泊松比和kn/ks及间均存在线性关系.如图9（d）和（e）所示，固定μ时，泊松比随刚度比增加呈线性增长趋势，各条曲线基本平行；摩擦系数的增大将引起泊松比的非线性减小，并且摩擦系数越小，减小幅度越大.

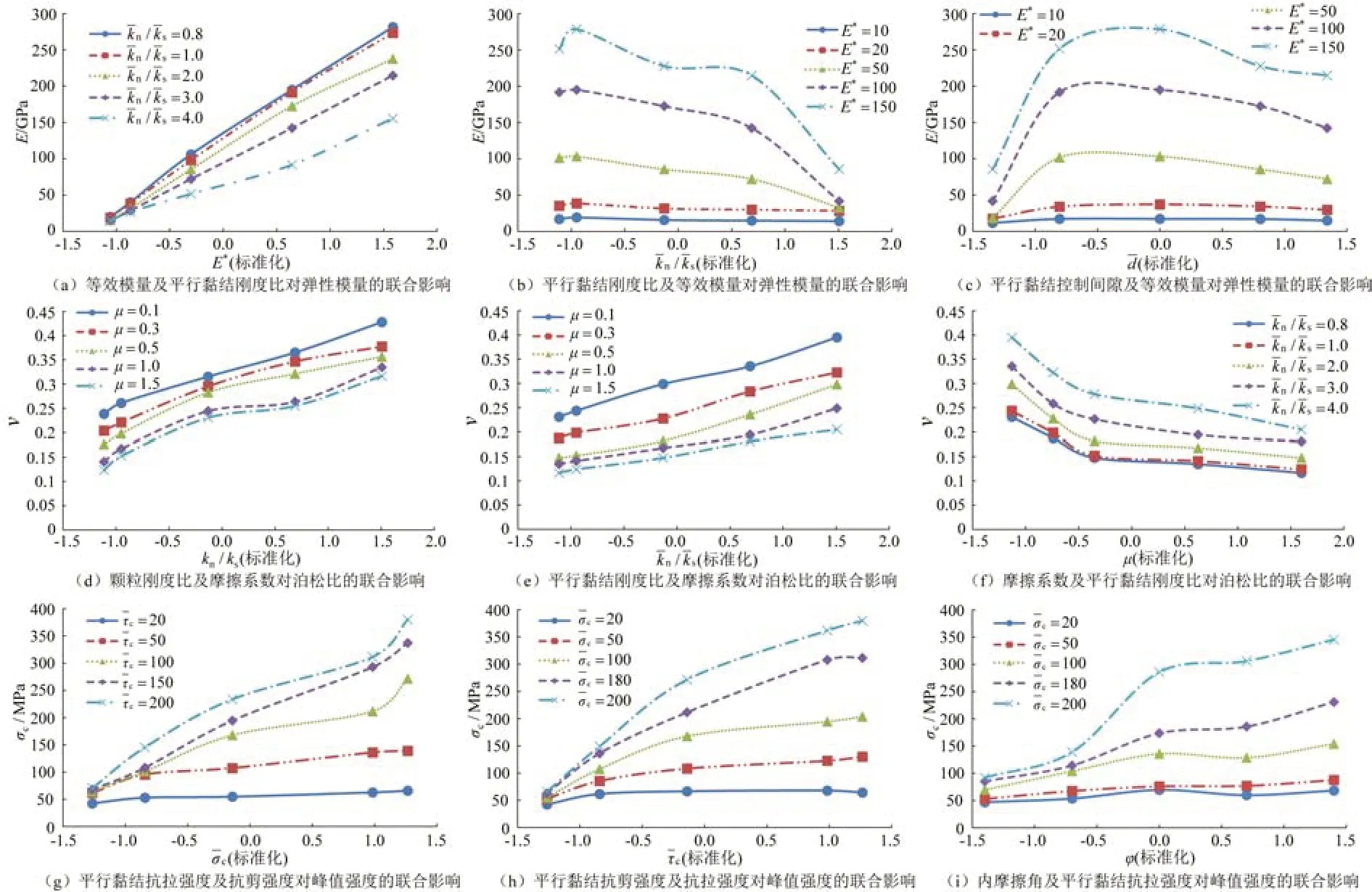
图9 多个细观参数对宏观参数的联合影响Fig.9 Joint effect of multiple meso parameters on macro parameters

4.2.3 多个细观参数对峰值强度的影响

5 讨论

利用PFC 从细观尺度研究材料的物理力学特性或进行岩土工程数值研究时，最重要的就是选取合适的细观力学参数，使其准确反映材料的宏观力学行为.以往细观参数标定问题多采用试错法且基于二维模型，一般通过将数值模型得到的宏观力学参数和室内试验的测定结果进行反复对比试错，直到数值计算结果与现场试验结果吻合.这种方法一般没有特定的规律可循，在一定程度上依靠研究者的经验；同时难以使用梯度算法，效率较低，往往会成倍地增加计算成本，且难以反映岩石在三维条件下的力学特性，在实际应用中遇到了较大限制.

本文的思路则是先利用BP 算法对复杂的标定模型进行轻量化，准确量化每个细观参数对宏观参数的影响，并筛选出对宏观参数有重大影响的关键细观参数.在算法方面，针对传统BP 算法效率低、稳定性不佳等缺陷，提出了引入陡度因子、自适应动量项及学习率的改进BP 算法，获得了良好的轻量化效果.通过分析宏细观参数间的相互作用规律，揭示了两种尺度参数间的作用机制并验证了轻量化分析结果的合理性.为PFC 参数标定研究提供了理论及数学模型.

然而，本文仍发现一些问题值得进一步讨论和研究：1）本文的轻量化分析成果主要基于平行黏结模型，在PFC 其他接触模型中的适用性还有待验证.2）尚未考虑clump 属性的影响，关于复杂颗粒在岩石宏细观参数标定中的作用今后还有待进一步研究.3）本文的研究成果主要用于减少宏细观参数分析模型中的变量个数并揭示两种尺度参数间的相互作用规律，以对PFC 细观参数标定问题提供数学模型，并未直接采用BP 算法对细观参数进行标定，标定方法部分后续将进行深入研究.

6 结论

本文从PFC3D 基本理论及宏细观定性关系入手，基于平行黏结模型，通过合理的试验设计及数据分析方法，对宏细观参数间的敏感性进行量化，提出了一种基于改进BP 算法的宏细观参数轻量化分析方法，可为PFC 细观参数标定问题提供一定参考.本文得到的主要结论如下：

1）通过在功能函数中引入陡度因子、自适应动量系数的Nesterov 动量法及自适应学习率提出了一种改进BP 算法并将其应用于PFC 细观参数轻量化处理问题中；在与传统BP 算法的对比中发现：改进算法的收敛速度提升了140%，避免了迭代中的震荡效应并使误差减小了47%左右.获得的结果更加准确合理，有效达到了宏细观参数分析模型轻量化目的.同时，本文提出的算法在水利及岩土工程领域中的相近问题上也具有一定适用性.

2）采用改进的BP 算法进行轻量化分析发现：等效模量、平行黏结刚度比及平行黏结控制间隙对岩石弹模有显著影响，其中等效模量起主导作用，另一方面改进BP 算法较传统方法明显的反映了刚度比对弹模的重要性；对泊松比影响较大的细观参数为平行黏结刚度比、颗粒刚度比及摩擦系数，本文算法在两个刚度比的重要性刻画上要稍准确一些；平行黏结抗压、抗剪强度及内摩擦角对峰值强度有控制作用.