盾构接收工作井围护结构附加应力计算及应用

杨果林 ，李海峰 ，袁志斌 ，肖洪波

（1.中南大学 土木工程学院，湖南 长沙 410075；2.中建五局 土木工程有限公司，湖南 长沙，410004）

随着我国市政交通等基础设施建设的快速发展，隧道及地下工程建设方兴未艾.盾构法因具有掘进速率快、对周边环境影响小、施工安全性好及机械化程度高等优点，在复杂环境的城市隧道建设中得到了广泛应用.尽管盾构施工技术近年来有了长足发展，但由于地质条件和施工工艺的限制，盾构施工不可避免地对周边环境产生一定的扰动，引起地面及建构筑物的变形或沉降［1-3］.

关于盾构隧道施工对周边环境影响的研究，谭师好［4］基于弹性力学Mindlin 解，推导出地层任意点在矩形顶管正面推力、顶管侧面摩擦力作用下以及地层损失的影响下的土体变形解.王涛等［5］运用圆孔扩张-剪切理论，考虑剪切力的影响，计算了盾构刀盘切削土体在开挖平面内引起的二维应力.赵玉勃等［6］基于弹性力学Mindlin 解，推导了盾构隧道施工时正面推力及盾壳与土体摩擦力所引起的周围土体附加应力沿圆周方向的表达式.武崇福等［7］基于弹性力学Mindlin 解，推导出了上部建筑荷载作用下盾构施工刀盘正面推力，盾壳与土体摩擦力引起周边土体附加应力的解析解.Sagaseta［8］结合镜像法基本原理，推出了处理土体损失引起的土体附加应力的计算公式.赵耀强等［9］采用数值模拟分析的方法对北京、上海、南京、杭州等不同地层条件下由盾构始发引起的地表沉降进行了预测研究，总结出各典型地区盾构始发施工对地表变形的影响规律.魏纲等［10］采用修正的随机介质理论简化方法分别计算先行盾构和后行盾构施工引起的地表沉降值，最终叠加得到双线水平平行盾构施工引起的地表总沉降，其与实测值比较吻合.冯国辉等［11］基于盾构开挖侧穿邻近桩基引起桩-土相互作用的实际工况，提出了一种可预测桩基水平变形的简化计算方法.陈仁朋等［12］基于BP神经网络（BPNN）和随机森林算法（RF）两种机器学习算法的多参数、非线性拟合能力，提出了预测盾构掘进过程中地表最大沉降以及纵向沉降曲线的预测方法.

上述研究对于认识和分析盾构施工对周边环境的影响具有一定的参考价值.值得注意的是，盾构接收过程中围护结构的安全稳定性至关重要，例如南京地铁2 号线盾构进入元通站右线南端头接收井洞门时，洞内发生涌水涌砂，迅速扩大形成塌方，造成盾构机被埋于塌陷土体中；北京地铁14 号线西铁营站—右安门外站盾构区间右线接收过程中引起的地面坍塌事故也显露出此类问题.为了分析盾构接收对工作井的影响，刘军等［13］依托北京地铁14 号线工程，提出了一种地下主动接收盾构的施工技术，并基于数值模拟方法，探讨了盾构掘进对地表变形及接收室封端墙的影响.崔铁军等［14］以某盾构接收井为工程实例，对基坑开挖过程中引起的扰动问题进行了数值模拟和现场监测对比分析，得出了以土钉、锚固和钢支撑等进行支撑的接收井较好地控制了地面沉降的结论.马烁［15］对盾构接收掘进前方土体变形进行研究，提出盾构在接收过程中，前方土体从半无限状态变化成有限状态，其过渡的界限在14～12 环左右的距离，同时提出了接收时土仓压力取值设定的建议.盾构接收在整个盾构隧道施工过程中所占空间较小，但是施工的风险性不容忽视.盾构在接收过程中，距离工作井越近，对工作井围护结构的扰动越大.但是，关于盾构接收期工作井围护结构附加应力的相关分析研究鲜见报道，无法实现盾构接收期工作井围护结构力学行为的理论分析，因此有必要对盾构接收期工作井围护结构附加应力进行分析研究.

本文以湖南某电力盾构隧道接收工程为背景，分析研究盾构接收阶段对工作井围护结构的影响.首先基于Mindlin 应力解与Sagaseta 解，分别计算盾构刀盘正面附加推力、盾壳与土体摩擦力、同步注浆压力和土体损失等对工作井围护结构所产生的附加应力，分析附加应力的主要影响因素.结合数值模拟，对依托工程工作井围护结构的力学行为进行分析研究，进一步探究掘进参数对工作井围护结构附加力的影响，提出盾构接收期掘进参数的设置原则，并在工程实践中予以应用评价，以期保障工程安全施工并为类似工程施工提供参考和指导.

1 盾构接收期工作井围护结构附加应力计算方法

1.1 盾构接收期工作井围护结构附加应力计算分析力学模型

如图1 所示，基于盾构接收期盾构和工作井空间及力学作用关系，通过对工作井围护结构和盾构机的简化，以盾构机盾体为主要分析对象，同时简化工作井维护结构为规则长方体，可得盾构接收期工作井围护结构力学模型.如图1 所示，建立右手直角坐标系，盾构掘进方向为x方向，z轴以地面为零点垂直向下穿过盾构刀盘中心，盾构机埋深为h，盾构机半径为R，盾构机长度为L.盾构刀盘正面附加推力和盾壳与土体摩擦力作用方向均沿盾构掘进方向，前者作用范围为刀盘与土体接触面，后者是盾体与土体接触面.同步注浆压力作用于盾构盾尾同步注浆区域，土体损失主要位于盾构刀盘后方区域.

为探究盾构接收时盾构刀盘正面附加推力、盾壳与土体摩檫力、同步注浆压力及土体损失对工作井围护结构的影响，作出如下基本假定：1）不考虑时间效应，只考虑推进时的空间变化；2）土体为各向同性线弹性均匀半无限体，不考虑盾构与接收井开挖后边界条件的变化；3）假定盾构刀盘正面推力和盾壳与土体摩擦力为均匀分布.

1.2 计算方法依据

如图2 所示，在各向同性的弹性半无限体中，距地表深度c处有一水平集中力P，作用于点（0，0，c），对于任意点（x，y，z）处的Mindlin 应力解［16］表达式为：

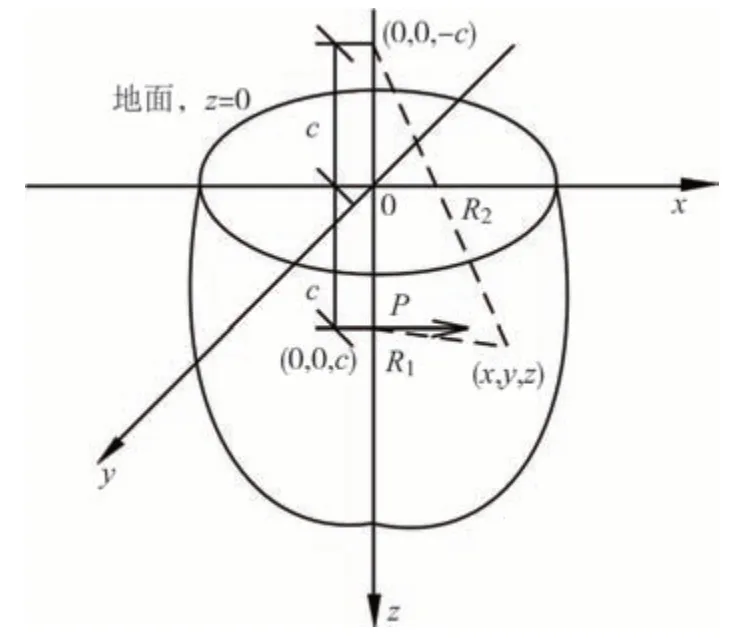
图2 水平力Mindlin解示意图Fig.2 Mindlin solution diagram of horizontal force

式中：P为切向集中力，kN；μ为土体泊松比.

如图3 所示，距地表深度c处竖向集中力P′作用于点（0，0，c），对于任意点（x，y，z）处的Mindlin 应力解表达式为：

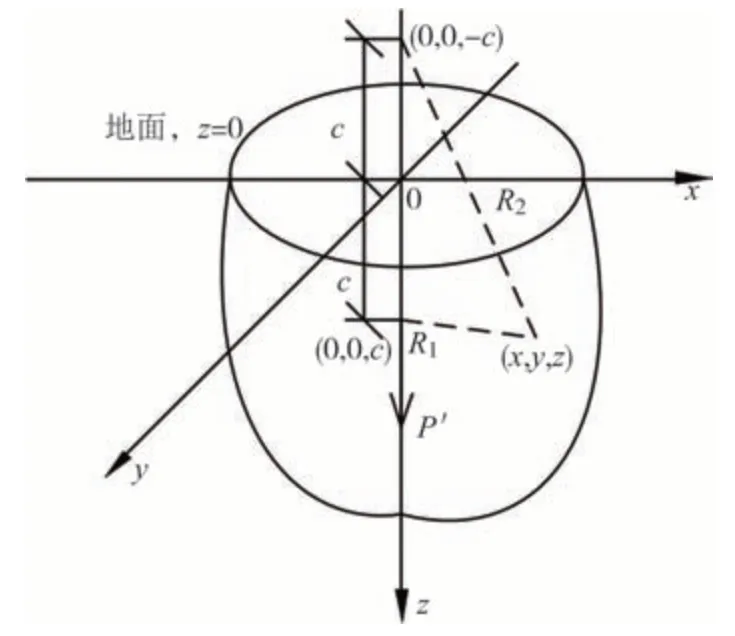
图3 竖向力Mindlin解示意图Fig.3 Mindlin solution diagram of vertical force

式中：P′为竖向集中力，kN.

1.3 各影响因素附加应力分析计算及总附加应力

1.3.1 盾构刀盘正面附加推力引起的附加应力

依据盾构工作机理和性状，本文仅考虑垂直作用在工作井围护结构上的附加力p1.基于水平力Mindlin应力解，对正面推力所在的圆面上进行积分.

如图4所示，设盾构开挖面中心点坐标（0，0，h），取圆形均布力微元，坐标为（0，rcosθ，h-rsinθ），对圆面进行积分可得：

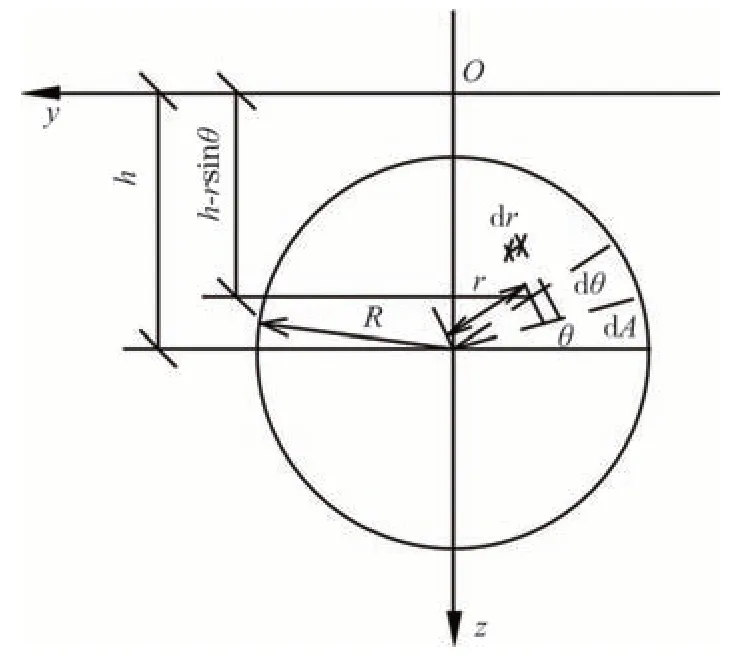
图4 正面附加推力示意图Fig.4 Schematic diagram of front additional thrust

式中：pz为盾构刀盘正面附加推力引起的附加应力，kPa；p1为刀盘正面附加推力，kPa；R为盾构机半径，m；h为盾构机埋深.

式（5）中盾构刀盘正面附加推力p1的物理意义为在盾构施工过程中，开挖面需要有足够的支护力以保持开挖面的稳定，具体计算取值时可以依据文献［17］按下式求得：

式中：Δp为刀盘切口切入土体产生的挤压力，kPa；E为刀盘前方土体弹性模量，kPa；v为盾构机推进速率，mm/min；ω为刀盘转速，rad/s；ξ为刀盘开口率，%；D为盾构机直径，m；k为刀盘分块数.

1.3.2 盾壳与土体摩擦力引起的附加应力

如图5 所示，R为盾构计算半径，设盾构机头部开挖面中心坐标为（0，0，h），盾构机长度为L.对于盾构机表面微元坐标（-l，Rcosθ，h-Rsinθ）沿机身圆柱面进行积分可得：

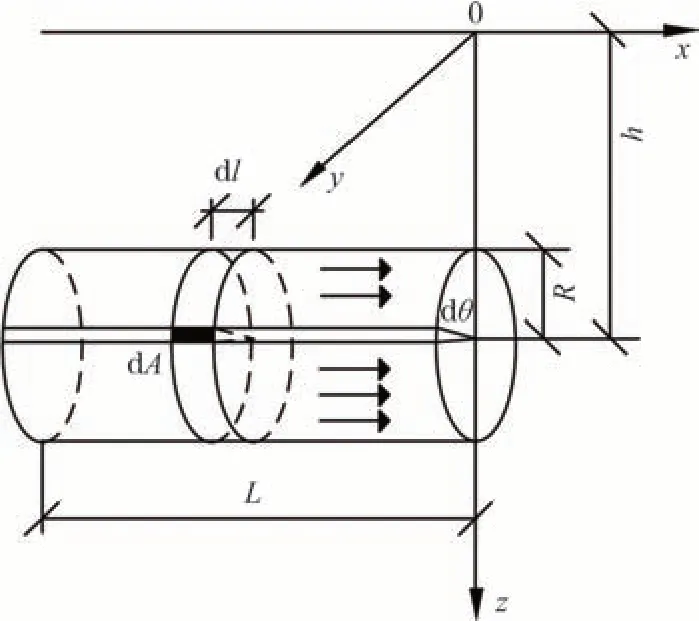
图5 盾壳与土体摩擦示意图Fig.5 Schematic diagram of friction between shield shell and soil

式中：pd为盾壳与土体摩擦力引起的附加应力，kPa；p2为盾壳与土体摩擦力，kPa；L为盾构机长度，m.

摩擦力损耗是盾构机主要能量损耗，盾构机掘进过程中盾壳与土体接触面在土压力的作用下产生摩擦力，主要包括自重引起的摩阻力以及四周土压力产生的摩阻力，朱合华等［18］提出摩擦力简化计算公式如下：

式中：K为盾壳土体之间的摩擦因数，砂土取值0.3～0.4，黏土0.2～0.3；W为盾构机单位长度自重，kN/m；γ为土的重度，kN/m3；φ为内摩擦角.

1.3.3 同步注浆压力引起的附加应力

同步注浆过程中，注浆量和注浆压力是两个关键参数.假定盾尾同步注浆压力为p3，作用范围为一环管片宽度B，均匀分布.设盾构机头部开挖面中心坐标为（0，0，h）.取坐标（-l，Rcosθ，h-Rsinθ）表面微元dP=p3Rdldθ，分解为水平分力dPh=p3Rcosθdldθ与竖向分力dPv=p3Rsinθdldθ，对高为B的圆柱面进行积分可得：

式中：pth、ptv、pt为同步注浆压力引起的水平、竖向及总附加应力，kPa；p3为盾尾同步注浆压力，kPa；B为一环管片宽度，m.

1.3.4 土体损失引起的附加应力

张润峰等［19］曾采用Pinto 等［20］提出的盾构隧道施工土体损失引起的地层位移解析解，并结合弹性力学公式，推导出土体损失引起的附加应力公式如式（19），本文采用其计算方法.

式中：ps为土体损失引起的附加应力，kPa；ux、uy、uz分别为x、y、z方向的位移；Vloss为土体损失率.

如式（20），联立上述盾构刀盘正面附加推力、盾壳与土体摩檫力、同步注浆及土体损失引起的附加应力计算公式，可得盾构接收到达时垂直作用于工作井围护结构的总附加应力，并采用科学计算软Matlab编制计算程序进行数值积分计算.

2 影响因素分析

根据对实际工程的观察，盾构刀盘正面附加推力和盾构与土体摩擦力是引起围护结构附加应力的主要因素.通过上文附加应力分析计算可知，正面附加推力主要与盾构掘进参数设置有关，盾壳与土体摩擦力主要和盾构隧道直径及开挖深度等因素有关.为此，下文首先对盾构隧道直径和开挖深度进行计算分析.

2.1 盾构机直径影响分析

城市地下盾构隧道工程中地铁隧道直径以6 m居多，近年来因使用需求增加而逐渐呈现直径增大的趋势.在地下管廊工程中盾构隧道直径则以4 m较为常见，因此下文分别计算盾构机直径为4 m、6 m、8 m 和10 m 时的围护结构总附加应力，以明确盾构机直径对工作井围护结构的影响规律.

分别取垂直于围护结构接收面沿深度总附加应力变化结果和盾构机中心线与围护结构接收面交点处总附加应力变化进行分析，得到图6.

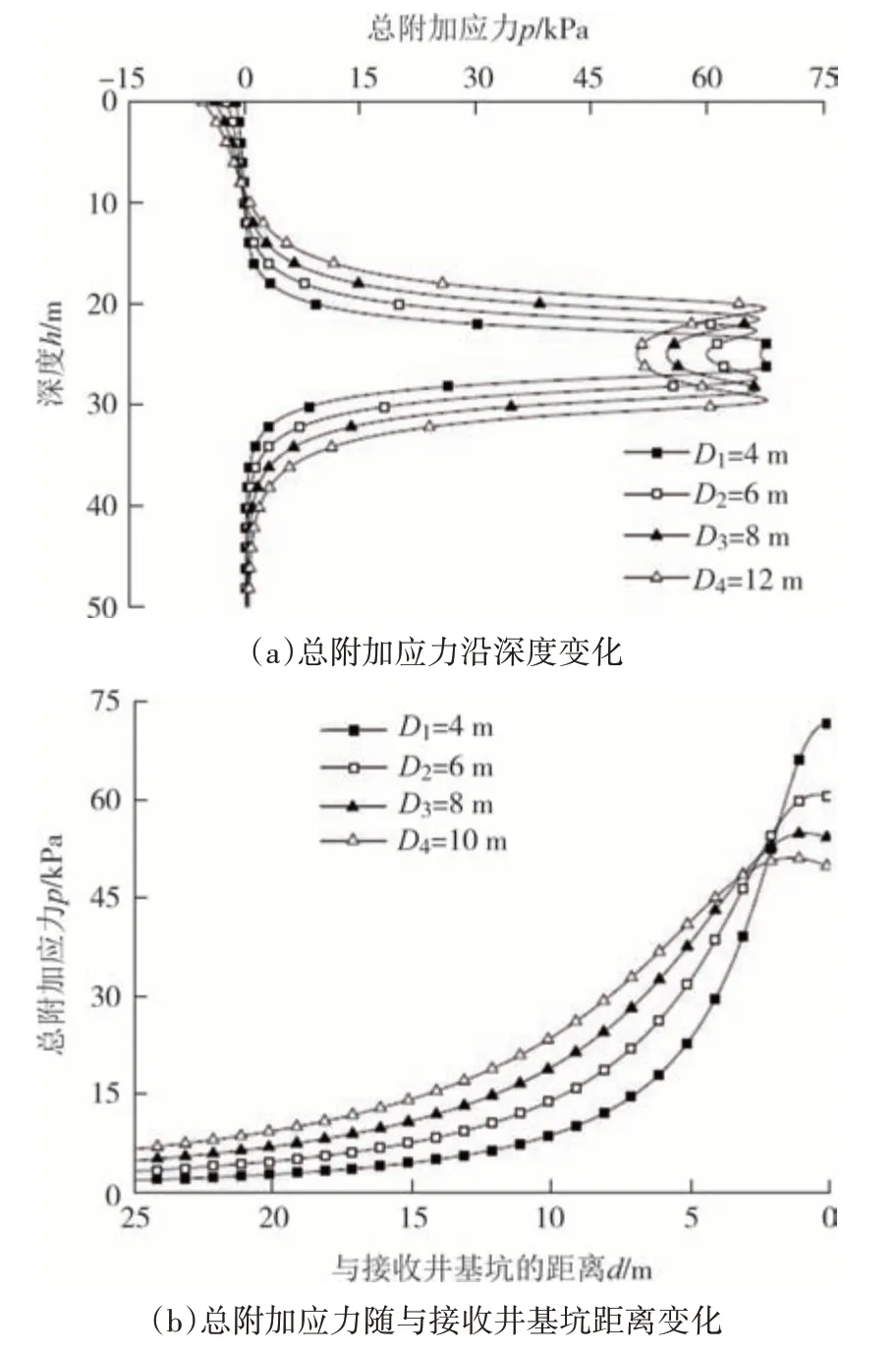
图6 不同直径下附加应力变化曲线Fig.6 Additional stress curve with different diameters

从图6中可以看出，盾构隧道直径增大时围护结构附加应力作用范围增大，且作用范围均在25m±1.5D（D为盾构机直径）内.同时，随着隧道直径增大，附加应力双峰值更加明显，中心点处的附加应力值减小，但附加应力最大值基本不变，均为70 kPa 左右.由此可知，盾构机直径增大会扩大附加应力影响范围，但是附加应力最大值保持不变.同时，从图6 中可以看到与接收井基坑距离大于2 m 时大直径盾构机产生的附加应力大，但当小于2 m 时小直径盾构逐渐超越大直径盾构，这是因为大直径盾构在靠近接收井时速率比小直径盾构减缓得快，因此附加应力增长速率小于小直径盾构，导致小直径盾构在接近接收井2 m以内附加应力超过大直径盾构.

2.2 开挖深度

为分析不同深度下盾构掘进附加应力变化规律，结合城市盾构隧道埋深区间情况，本文分别计算深度为10 m、15 m、20 m 和25 m 时的围护结构总附加应力.同上分析，取垂直于围护结构接收面沿深度总附加应力变化结果和盾构机中心线与围护结构接收面交点处总附加应力变化进行分析.

从图7 可以看出，抵达接收井时盾构隧道所处深度为10 m、15 m、20 m和25 m时总附加应力最大值分别为49.84 kPa、58.35 kPa、65.4 3kPa 和71.74 kPa，表明附加应力最大值随盾构机所处深度的增加而增加，而附加应力的影响范围变化较小.综上所述，围护结构的附加应力最大值主要受隧道深度影响，隧道直径对附加应力分布范围具有影响，因此当盾构隧道直径或所处深度增加后，应预测分析盾构接收时对围护结构附加应力的影响范围及大小，制定和采取切实可行的工程措施进行安全控制，防止围护结构因附加应力过大而发生失稳.

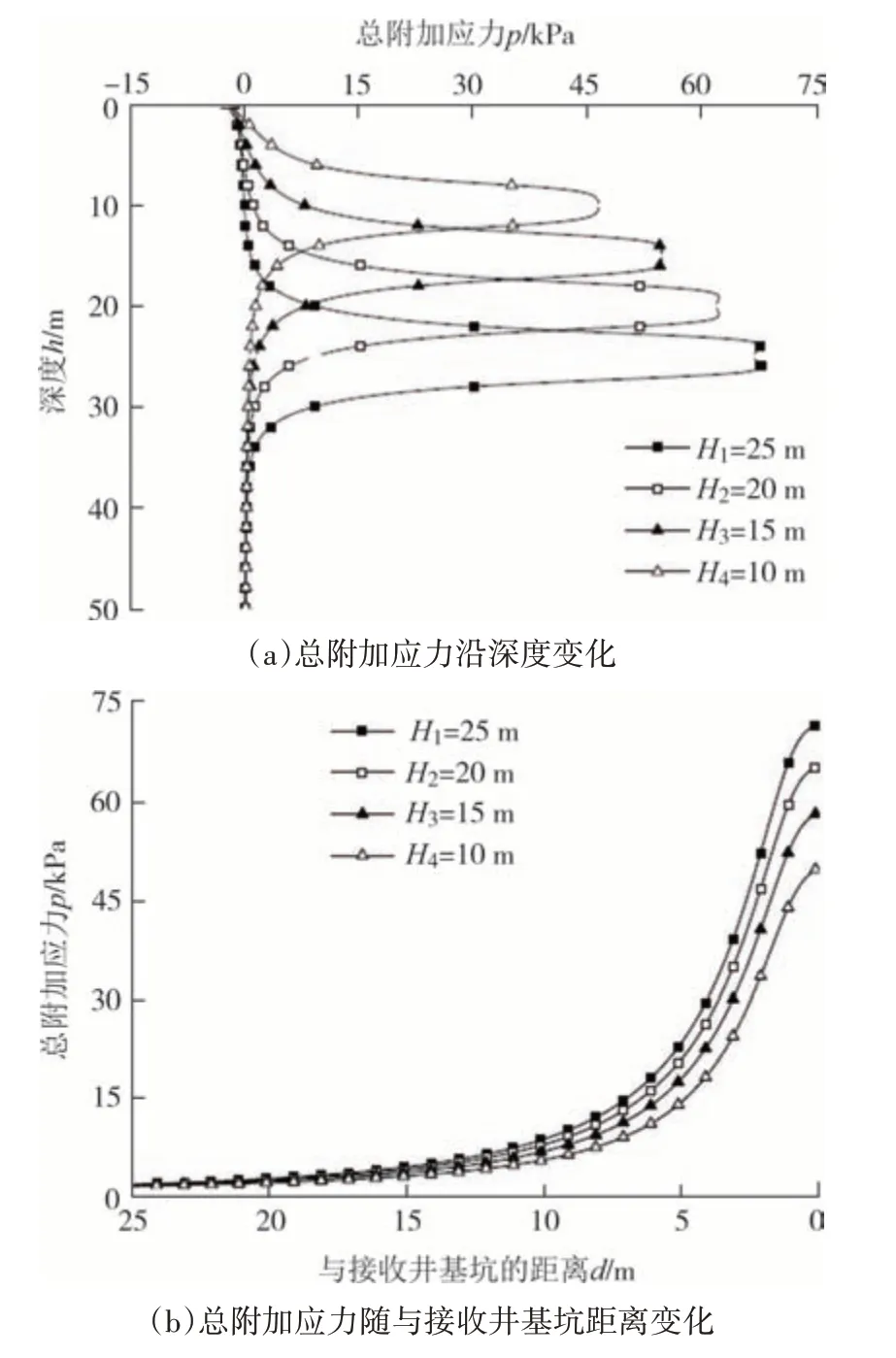
图7 不同深度下附加应力变化曲线Fig.7 Additional stress curve at different depths

3 工程案例分析

3.1 工程概况

湖南某电力盾构隧道新增工作井，如图8 所示.该隧道内径3.6 m、外径4.1 m，隧道中心点距地表25 m.盾构机为土压平衡盾构机，盾构机主机身长7.8 m，盾构机的开口率ξ=38%，刀盘分块数k=8，质量约为280 t，管片宽度1 m 和1.2 m.如图9 所示，接收工作井开挖深度29 m，围护结构采用地连墙加内支撑的形式，共设置6道支撑.

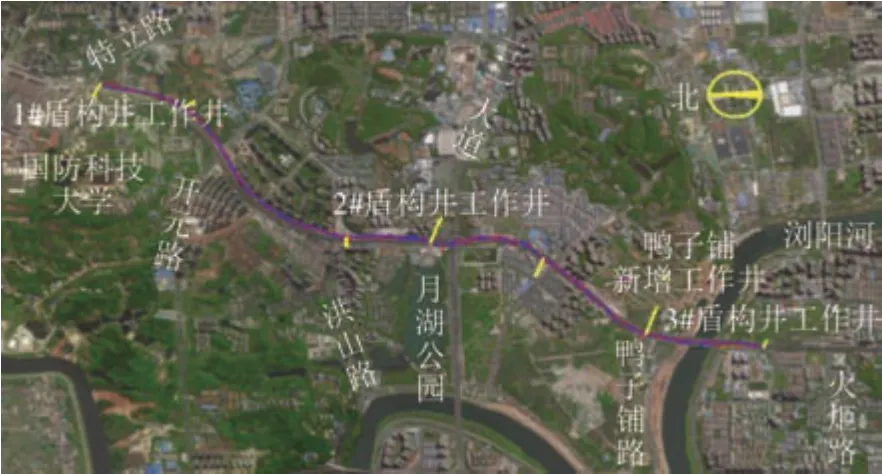
图8 电力盾构隧道工程平面图Fig.8 Power shield tunnel plan

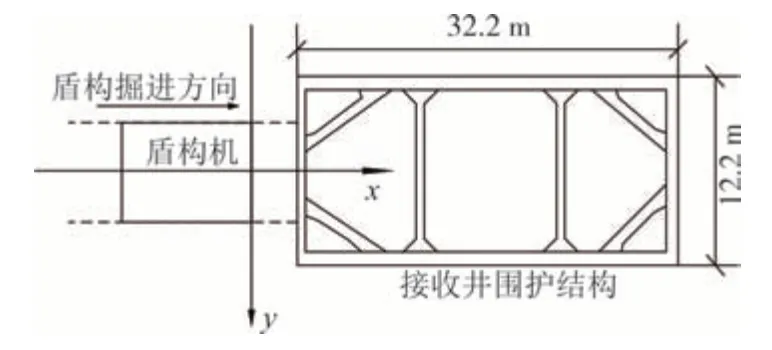
图9 盾构接收示意图Fig.9 Schematic diagram of shield tunneling reception

盾构接收段主要穿过粉质黏土层，相关参数取值如下：土层平均弹性模量E为28.5 MPa，泊松比为0.3，土层平均重度为19.6 kN/m3，盾构与周围土体界面摩擦角为18°.根据工程案例参数和上文相关计算公式，取正面附加推力为60 kPa，盾壳土体摩擦力为81 kPa，同步注浆压力为0.25 MPa，土体损失率为1%.

3.2 各附加应力计算分析

3.2.1 正面附加推力的附加应力

刀盘正面附加推力作用下，垂直于基坑接收面围护结构附加应力随基坑深度变化如图10 所示，盾构接收施工对围护结构表现为挤压作用.最大值出现在盾构中心点深度25 m 处，为24.25 kPa，附加应力影响范围约为25 m±1.5D，当深度大于31 m（25 m+1.5D）或小于19 m（25 m -1.5D）时，附加应力趋于零.x为开挖面与接收井围护结构距离，当x减小时表示盾构离工作井越来越近，附加应力逐渐增大.其中，当x小于6 m（1.5D）时，附加应力增加幅度较大，6 m 到4 m 附加应力最大值从3.57 kPa 增加至7.01 kPa，增加了0.96 倍；从4 m 到2 m 时附加应力最大值从7.01 kPa 增加至16.36 kPa，增加了1.33 倍.综上可知，正面附加推力附加应力主要作用范围是以盾构中心点为圆心，直径3D的圆形范围，从工程施工的角度来说，正面附加推力大小主要与盾构掘进参数有关.

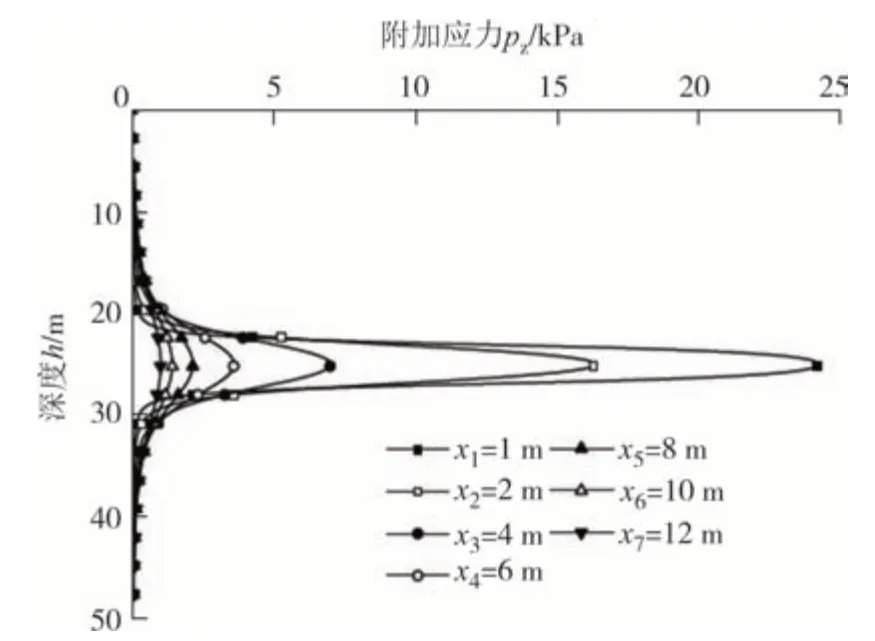
图10 正面附加推力的附加应力Fig.10 Additional stresses for front thrust

3.2.2 盾壳与土体摩擦力的附加应力

盾壳与土体摩擦力作用下，围护结构附加应力随基坑深度变化如图11 所示.可以看出，附加应力曲线呈有峰值的尖角分布，极大值出现在25 m±0.5D深度处，附加应力竖直方向的影响范围约为±2.5D，相较于正面推力影响范围更大.当深度大于35 m（25 m+2.5D）或小于15 m（25 m-2.5D）时，附加应力趋于零.综上可知，盾壳与土体摩擦附加应力主要作用范围是以盾构中心点为圆心，直径5D的圆形范围，从工程施工的角度来说，盾壳与土体摩擦力大小主要与土体和盾构机之间的摩擦因数、盾构机直径、所处深度等因素有关，这些因素不易控制.

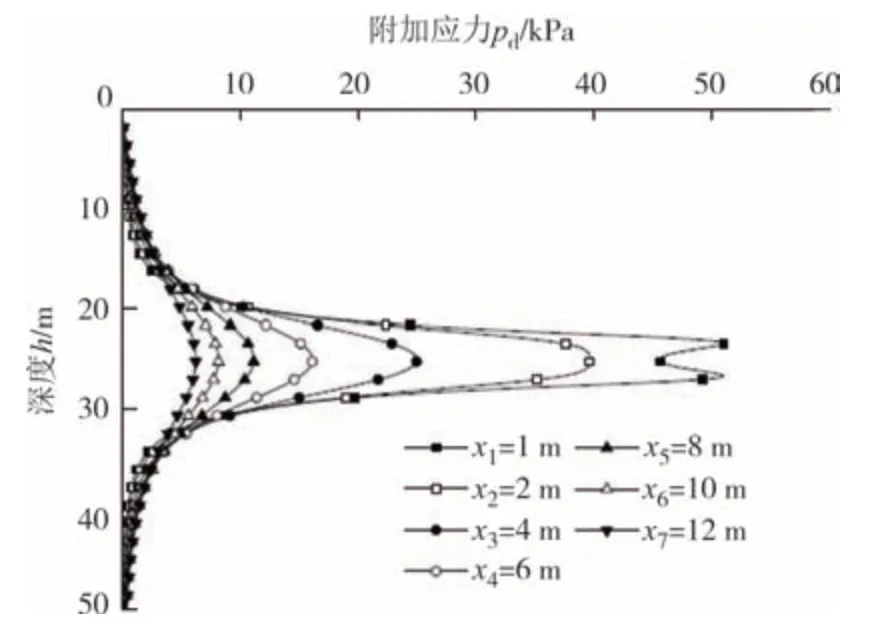
图11 盾壳与土体摩擦力的附加应力Fig.11 Additional stress of friction between shield shell and soil

3.2.3 同步注浆压力与土体损失的附加应力

同步注浆压力与土体损失附加应力如图12 和图13 所示.从图12 中可看出，同步注浆附加应力曲线同样呈现尖角分布，极大值出现在深度25 m 处，同步注浆附加应力作用范围为25 m±1.5D.当接收距离x小于10 m（2.5D）时，同步注浆附加应力增长明显，但是由于同步注浆附加应力数值较小，最大值约为0.8 kPa，相比于正面推力附加应力和盾壳与土体摩擦附加应力，可以忽略不计.

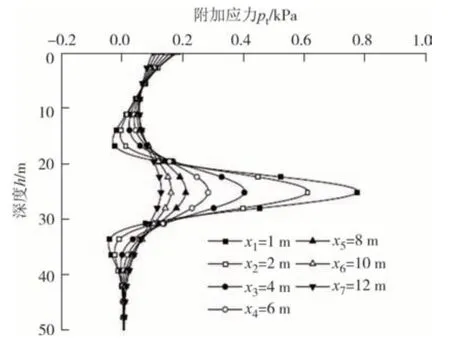
图12 同步注浆附加应力Fig.12 Additional stress of simultaneous grouting

从图13 中可以看出，土体损失附加应力对围护结构表现为卸载作用，附加应力压应力为正，拉应力为负，土体损失附加应力为负值.附加应力曲线呈尖角分布，极大值在深度25 m处.土体损失附加应力影响范围为25 m±2.5D，当深度大于35 m（25 m+2.5D）时附加应力趋于零，当深度小于15 m（25 m-2.5D）时，附加应力趋于0.5 kPa，最大值约为-4.3 kPa.

综上可知，同步注浆附加应力最大值仅为 0.8 kPa，而土体损失附加应力为负值，对围护结构表现为卸载作用，相比正面推力附加应力和盾壳与土体摩擦附加应力可以忽略不计.

3.3 总附加应力

综合上述正面附加推力、盾壳与土体摩擦力、同步注浆及土体损失引起的各附加应力，获得总附加应力变化曲线，如图14所示.从图14中可以看出，随着盾构接近接收工作井，总附加应力逐渐增大.当推进距离小于10 m 后，附加应力逐渐增加，此时主要是盾壳与土体摩擦力所引起的附加应力增长较多.当距离小于6 m（1.5D）时，正面附加推力引起的附加应力开始明显增大.总附加应力最大值约为73 kPa，其中主要为正面附加推力和盾壳与土体摩擦力引起的附加应力，正面附加推力引起的附加应力约占总附加应力的37.5%，盾壳与土体摩擦力所引起的附加应力约占总附加应力的62.5%，其他因素影响占比相对较小.

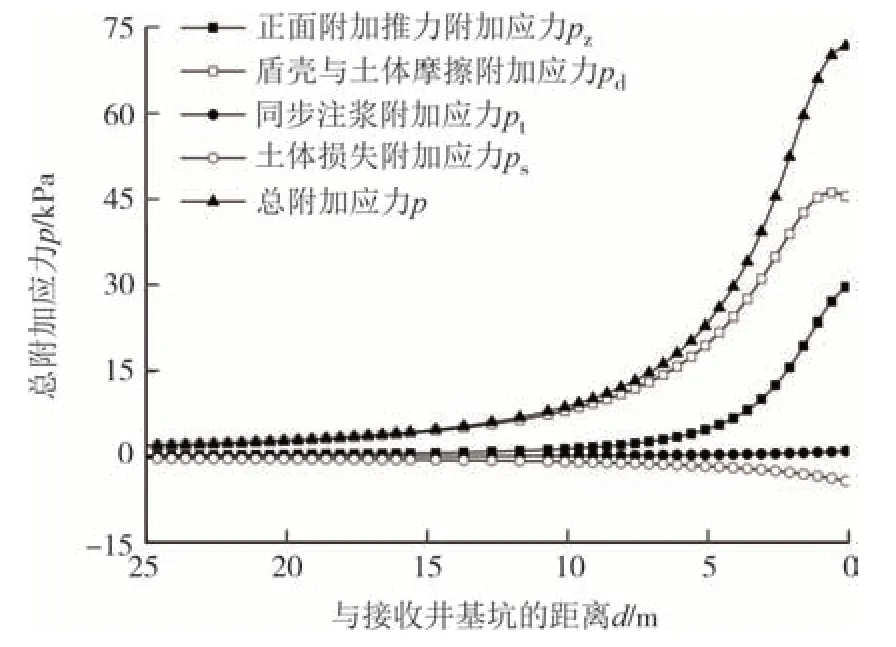
图14 总附加应力随距离变化图Fig.14 Diagram of total additional stress versus distance

3.4 数值模拟

3.4.1 接收模型建立

采用PLAXIS 3D 建立接收模型，模拟盾构接收过程.根据前文接收附加应力计算结果可知，盾构在距离接收井10 环之后，附加应力才有明显增长，因此接收段模型从与接收井15 环的距离开始模拟.模型三维尺寸为60 m×80 m×70 m，基坑尺寸12 m×22 m×40 m.盾构段采用板单元模拟盾构机身，实体单元模拟管片；同步注浆压力、盾构机摩擦力、正面附加推力采用面荷载模拟.

接收井模型地质参数以及围护结构参数，均按照前文工程概况中的介绍取值.盾构隧道采用1 m宽混凝土管片，厚度为0.25 m.隧道内径3.6 m，外径4.1 m，采用C50混凝土.模型中采用实体单元进行模拟，弹性模量取 31 GPa；泊松比取 0.25；材料重度取25 kN/m3.同步注浆压力取土压力大小，顶部取200 kN/m2随深度递增，变化率20（kN·m-2）/m；正面附加推力取200 kN/m2随深度递增，变化率 14（kN·m-2）/m；盾构机与土体摩擦力均匀分布，取 80 kN/m2.

3.4.2 围护结构总附加应力分析

整理数值模拟结果中接收阶段围护结构总附加应力与前文中理论推导计算出的总附加应力对比，如图15 所示.对比图（a）与（b）可以发现，模拟结果与理论计算结果相近，数值模拟计算最大总附加应力大于理论计算结果，模拟曲线明显存在双峰值.其原因在于，本文计算方法采用弹性力学Mindlin 解，假设土体为各向同性线弹性均匀半无限体，不考虑盾构与接收工作井开挖后边界条件的变化.而实际上随着盾构距离接收工作井越近，盾构前方土体变成了有限的土体［15］，工作井围护结构的存在，使盾构前方土体的边界发生变化，造成总附加应力理论计算值偏小，但是总附加力整体变化规律仍具有可靠性，说明本计算方法仍具有一定的合理性和适用性.

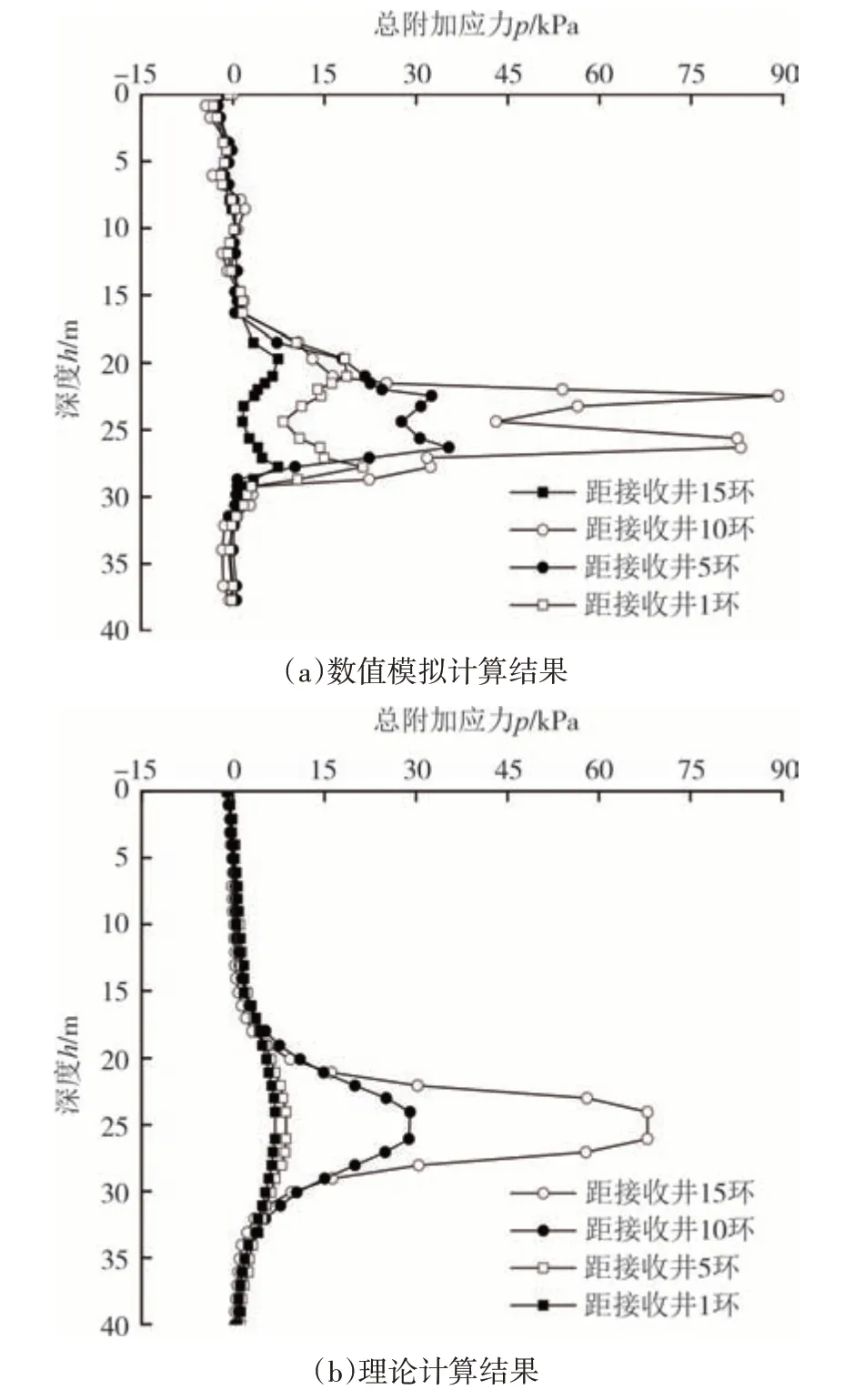
图15 总附加应力模拟结果对比Fig.15 Comparison of simulation results for total additional stress

3.4.3 接收阶段围护结构弯矩分析

盾构接收阶段工作井围护结构弯矩的数值模拟分析结果如图16 所示，可以看出，盾构进入接收阶段时，弯矩变化主要发生在深度25 m±5 m 范围内，这与计算方法分析的总附加力主要变化范围基本一致.当盾构距接收工作井15 环至10 环时，弯矩增量较小，而10环至5环时，最大弯矩从283 kN/m增加至385 kN/m，增长36%，特别是当5 环至0 环时，最大弯矩从385 kN/m 增加至820 kN/m，增长了113%，说明盾构接收距离越小，工作井围护结构弯矩越大，需引起重视.

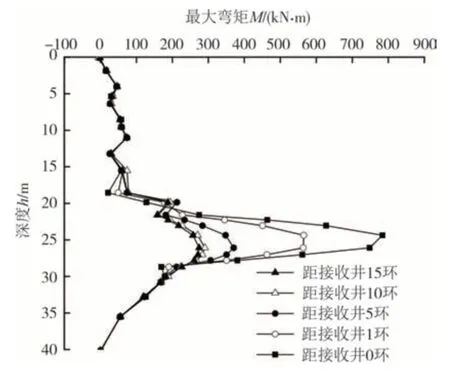
图16 接收阶段围护结构最大弯矩图Fig.16 Maximum bending moment diagram of enclosure structure in receiving stage

3.4.4 接收阶段围护结构变形分析

盾构接收阶段围护结构变形的数值模拟分析结果如图17 所示，可以看出，随着盾构接收距离减小，接收侧围护结构在盾构接收阶段变形明显增加，而对围护结构其余侧影响较小.接收完成后接收侧最大水平变形值30.01 mm，相较于开挖阶段增长13.92 mm，增长幅度为86.51%，接收距离从10环至0环时总位移增加12.86 mm，占总增量的92.37%，说明盾构的接收掘进施工对围护结构接收侧位移产生了显著影响，应该合理控制其位移发展.

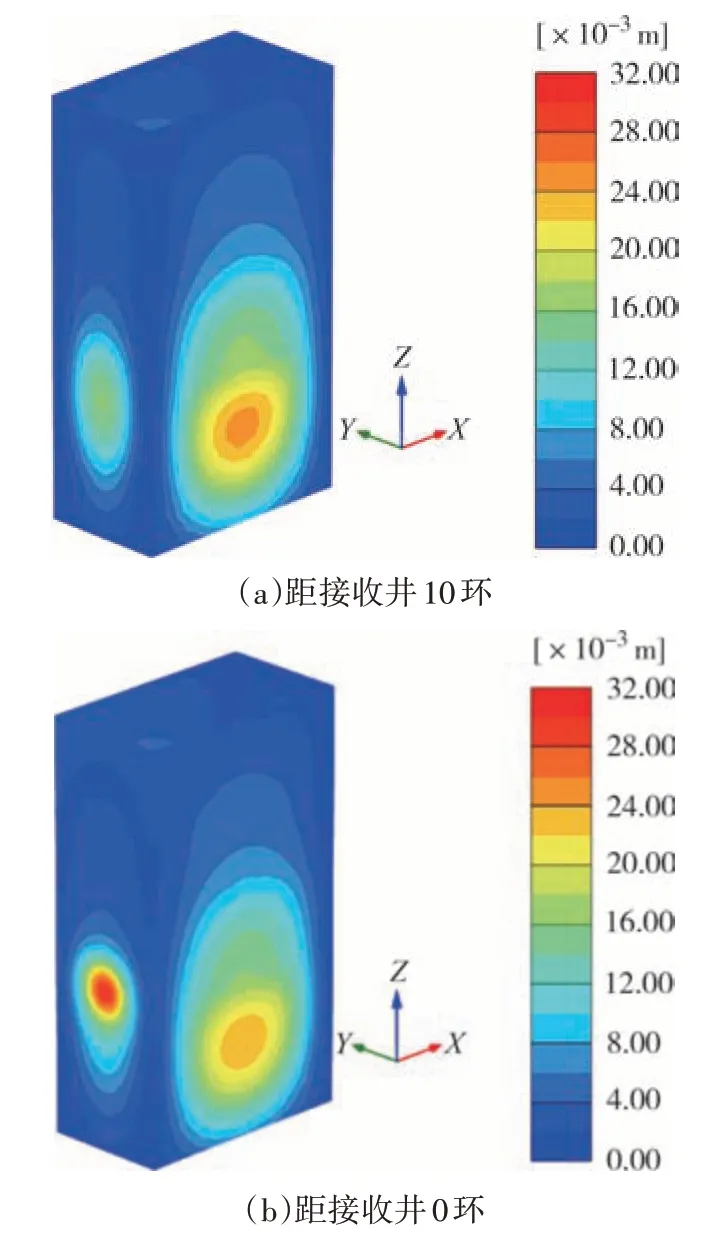
图17 接收阶段围护结构位移云图Fig.17 Displacement cloud of enclosure structure in receiving stage

综上可知，盾构接收阶段工作井围护结构的弯矩和变形均有明显增长，对于依托工程而言，在盾构进入接收阶段时应该采取优化控制措施，以有效控制围护结构附加应力，实现盾构的安全快速接收.

3.5 工程应用

通过上文附加应力工程案例计算结果可知，正面附加推力和盾构与土体摩擦力是引起围护结构附加应力的主要因素.正面附加推力主要与盾构掘进参数设置有关，盾壳与土体摩擦力大小主要与土体盾构机之间盾构隧道结构尺寸和隧道所处深度等因素有关.在施工时，盾构隧道尺寸和开挖深度主要由设计方案根据工程地质及工程目的设计决定，难以更改，因此对于现场施工具有重要指导意义的是盾构掘进参数的设定调整.从式（6）可知，正面附加推力主要与盾构机推进速率和刀盘转速有关，而在本工程中由于施工段地质条件较好，盾构机刀盘转速变化范围较小，因而主要通过控制盾构掘进速率来控制正面附加推力产生的附加应力.

为指导工程施工，根据工程实际情况、前期盾构推进速率分布情况及盾构机工作性能，选取110 mm/min、90 mm/min、70 mm/min、50 mm/min、30 mm/min 五个盾构推进速率，分别计算不同推进速率下工作井围护结构的总附加应力.

从图18 中可以看出，围护结构附加应力和推进速率呈正相关，推进速率越小，围护结构的附加应力越小.推进速率为110 mm/min、90 mm/min、70 mm/min、50 mm/min、30 mm/min 时，最大总附加应力分别为81.05 kPa、76.23 kPa、71.74 kPa、66.57 kPa、61.74 kPa，呈线性减小的趋势.推进速率对围护结构的附加应力影响范围亦集中于深度25 m±0.5D范围内，深度25 m±0.5D范围外的附加应力值基本不变.上述说明当推进速率减小时，正面附加推力引起的附加应力减小，从而使得总附加应力减小.由此可知，当盾构进入接收阶段时，可以采用“低推速”的原则以控制围护结构附加应力的增加.

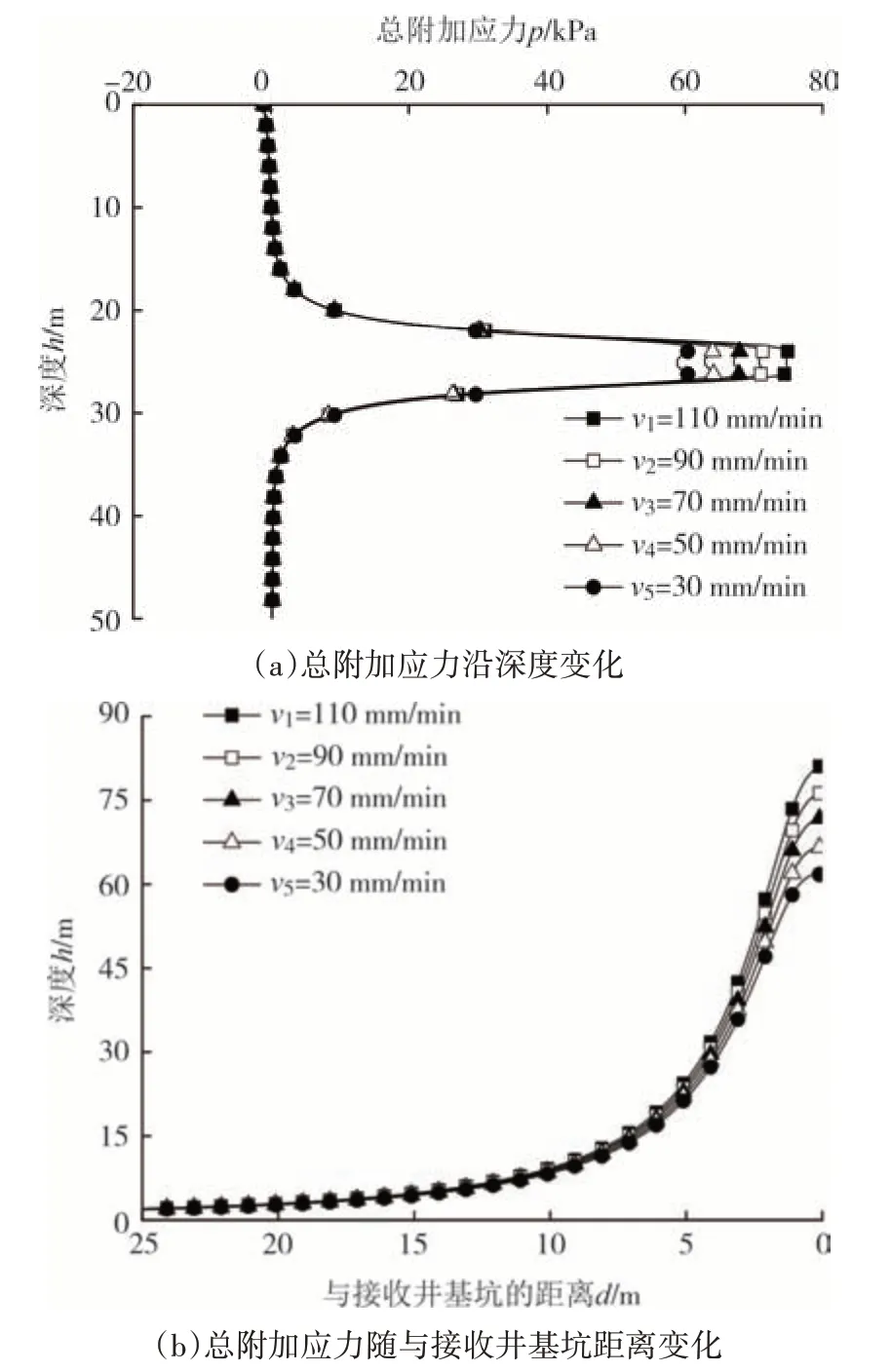
图18 不同推进速率下总附加应力变化曲线Fig.18 Change curve of total additional stress at different propulsion speeds

根据分析结果，在依托工程盾构接收期，采取了“低推速”的掘进参数设置原则.如表1 所示，通过对盾构接收前后推进速率的采集和统计（其中，盾构推进速率统计数据采自盾构机自动保存系统，其采集频率为1 次/s，分析时将每环的非掘进时间内的数据予以剔除），发现盾构接收前（64 环至52 环）推进速率分布于0～160 mm/min，平均值为76.38 mm/min；而在接近接收井时（11 环至0 环），推进速率在0～180 mm/min，平均值为51.57 mm/min.进一步，接收前（64环至52环）推进速率分布于80～120 mm/min的占比达到56.71%，而接收时（11 环至0 环）推进速率在40～80 mm/min 的占比为43.74%，更有33.67%的推进速率在0～40 mm/min，盾构接收期推进速率明显降低，使正面附加推力引起的附加应力减小，总附加应力降低，确保了本工程的安全顺利接收作业.

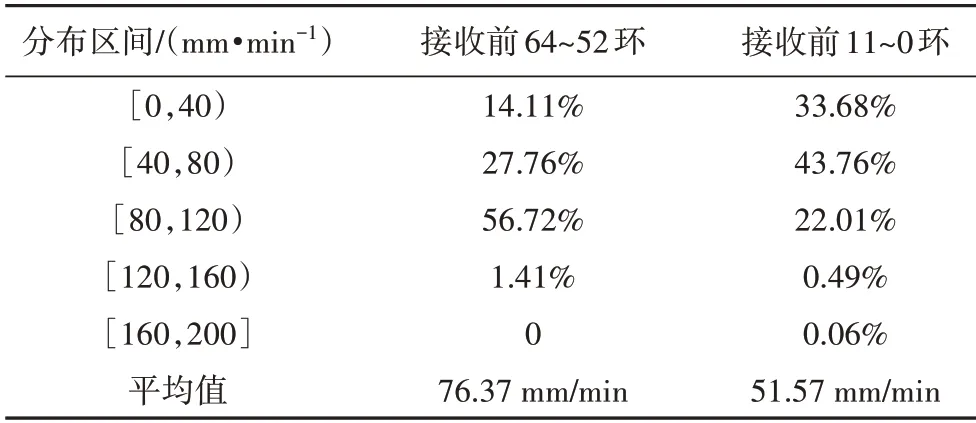
表1 推进速率分布占比统计表Tab.1 Propulsion rate distribution table

4 结论

1）基于Mindlin 解提出了盾构接收期工作井围护结构附加应力计算方法，分析表明随着盾构接近接收工作井围护结构，总附加应力逐渐增大，掘进距离小于10 m 后，附加应力增加明显.正面附加推力、盾壳与土体摩擦力和同步注浆压力对接收井围护结构所产生的附加应力主要为压应力，体现为挤压作用；土体损失引起的围护结构附加应力为拉应力，体现为卸载作用.

2）分析发现盾构隧道直径和开挖深度对工作井围护结构附加应力具有重要影响，盾构隧道直径从4 m增加到10 m，围护结构总附加应力双峰值影响范围增加了约300%，而附加应力值变化不大；盾构隧道开挖深度从10 m 增加至25 m，总附加应力值增加了约43.9%，而附加应力影响范围变化不大.这说明盾构隧道直径和开挖深度分别是影响总附加应力作用范围和大小的主要因素，因此当盾构隧道直径或所处深度增加后应注意围护结构的整体稳定性.

3）针对实际工程，分别计算分析了各因素对围护结构附加应力及总附加应力的影响规律，并结合数值模拟验证了计算方法的适用性和合理性.发现总附加应力中以正面附加推力和盾壳与土体摩擦力引起的附加应力为主，分别约占比37.5%和62.5%，最大值分别约29.57 kPa 和45.99 kPa.同步注浆引起的附加应力最大值约为0.8 kPa，土体损失引起的附加应力极值约为-4.3 kPa，相比于前两种附加应力可以忽略不计.数值模拟表明盾构进入接收阶段，工作井围护结构的弯矩和变形都有明显增长，因此应采取优化措施控制盾构接收对围护结构的影响.

4）基于控制掘进参数的施工理念，通过采取“低推速”的方法，主动降低盾构接收期关键阶段（10～0环）推进速率，进而有效降低了盾构正面推力，减小了围护结构附加应力，实现了盾构安全接收施工目标.