启动方式对混流泵噪声特性的影响

朱国俊，唐振博，冯建军，罗兴锜

（西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048）

0 引言

泵作为一种典型的水力机械，在国民经济发展中担任着重要的角色[1]。近年来，随着南水北调工程的进一步发展，众多大型调水工程投入生产，大型水泵得以应用。但大量的运行实践表明，对于泵站，其事故往往发生在水力机组过渡过程中。在过渡过程中，压力、振动参数可能会比常规运行工况大得多，从而可能引起压力管道破裂、调压室损坏和机组部件破坏等严重事故，对泵站产生非常严重的影响[2]。混流泵是一种介于离心泵和轴流泵之间的一种泵型，具有结构简单、抗汽蚀性能好的特点，广泛应用于农田水利、农业灌溉、市政给排水等领域[3-4]，其性能优化方法也获得了研究[5-6]。随着混流泵应用领域的不断深入发展，众学者对其瞬态性能愈发关注[7-10]。

混流泵的启动过程是一个极其复杂的瞬态过程，在启动过程中，混流泵的扬程、效率等外特性参数和流场分布会发生剧烈变化，可能会造成冲击负载、水力激振和空化破坏等现象，对泵的稳定运行产生负面影响[11-12]。其中，稳定性恶化的外在表现为泵体出现剧烈振动、泵内部流体的压力脉动幅值剧增以及泵体出现强烈噪声[13-15]。因此，为提升混流泵机组在启动过程中的稳定性同时控制其在启动时产生的噪声辐射水平，对混流泵启动过程中泵体处的噪声特性进行研究十分必要。

目前，国内外学者开展混流泵等水力机械启动过程相关研究的方法主要包括数值模拟与试验研究两种，并取得了有指导意义的成果。在泵启动过程中的内部流动机理研究方面，数值模拟方法应用较多，如罗陈杰等[16]基于流体动力学模拟软件对混流泵启动过程中的水动力瞬态特性进行了数值计算，发现启动过程中泵内压力逐步增加，压力最高处集中在叶轮与导叶交界处；戈振国等[17]揭示了大流量工况下离心泵断电后特性参数的变化滞后于设计工况，但总体值较小；FERNANDEZ 等[18]发现非定常数值计算方法可以有效地模拟混流泵内部复杂的流动现象；鲁阳平等[19]建立了一套混流泵启动过程瞬态性能理论预测模型，研究发现混流泵瞬态扬程可分为稳态项、加速项和惯性项扬程，且加速项扬程和惯性项扬程在启动过程中影响较大。相比于数值模拟计算，试验研究更能接近于实际应用场景。因此LU 等[20]通过一种同步采集实验系统对混流泵线性启动过程开展了研究，发现在不同加速时间的快速启动过程中，对应于短加速时间的强加速度将使叶轮空化得到抑制；李伟等[21]通过对混流泵启动过程瞬态外特性和压力脉动测量系统，发现在快速启动条件下，启动结束时刻主频压力幅值存在由压力冲击造成的极大值；王乐勤等[22-23]通过试验对混流泵的启停、瞬态调阀与调速进行研究，研究发现启动过程存在冲击效应，并整理出了混流泵在启动过程中的瞬态水力特性解析式。通过对上述学者的研究总结可以看出，对混流泵启动过程的研究目前集中在泵的外特性与压力脉动变化上，而仍然缺乏关于启动过程中泵内部流动诱导的外场噪声变化规律研究。目前，对混流泵的启动过程研究大多都是在线性启动条件下完成，而对非线性启动过程的研究极少。马凌凌[24]仅对混流泵指数启动下的扬程与流量进行了理论模型计算，研究发现马鞍区对指数启动条件下的瞬态特性无明显影响。

为了分析非线性和线性启动方式对混流泵启动过程中稳定性的影响，本文通过声振测试系统同步采集了不同启动方式下混流泵的外场噪声、压力脉动和主轴振动信号，然后基于信号处理方法和相干性分析方法对采集到的多物理场信号进行了研究，以期揭示非线性和线性启动方式对混流泵外场噪声的影响规律，并获得与噪声关联的主要因素，为提高混流泵启动过程中的稳定性提供基础。

1 试验装置与模型泵

1.1 混流泵试验装置

本文研究对象为半开式混流泵装置，其工作介质为常温水。该模型叶轮叶片数为4，正常运转状态下的额定转速为nr=1 800 r/min，因此稳态轴频fn=30 Hz，叶片通过频率fBPF=4fn=120 Hz。试验泵如图1 所示，试验泵段叶轮的几何参数如表1。为采集不同启动方式下混流泵处的噪声、压力脉动和主轴振动信号，构建包含声学传感器、压力脉动传感器及激光测振仪的多通道同步测试系统。

表1 混流泵叶轮主要参数Table 1 Parameters of mixed-flow pump impeller

1.2 测试系统与试验方法

本次试验在自行搭建的混流泵闭式试验台上进行。混流泵的驱动装置为变频电机，采用可编程逻辑控制器进行控制。变频电机为YVF2-90S-2 型三相异步电动机，其额定频率为50 Hz，恒转矩频率范围为3～50 Hz。变频器为浙江得弗公司的DV-4T1.5G/P。泵的进出口压力采用麦克公司的MDM3051S 型智能压力变送器进行测量，精度为±0.075%。扭矩采用精度为0.2 级的扭矩传感器进行测量，试验过程中的流量采用电磁流量计进行测量，电磁流量计的测量精度为±0.2%。混流泵的多物理场测试系统示意图如图1a 所示，噪声、压力脉动及主轴振动测点布置场景如图1b 和图1c 所示。麦克风支架将声学传感器对准叶轮出口与导叶进口间的无叶区中部，并按照GB/T29529-2013 规定使其与壳体壁面保持1 m 的距离。混流泵的启动试验在出口阀全开的情况下开展。

试验中所用声学传感器如图1b 所示。该声学传感器为美国PCB 公司的130F20，灵敏度为45 mV/Pa，其可在-10～50 ℃的条件下工作，可测声信号的频段范围为10～20 kHz，因此可用于捕捉快速启动条件下混流泵叶轮处的噪声信息。试验中采用的压力脉动传感器为美国PCB 公司的M112A22 通用型石英压力传感器，灵敏度为14.5 mV/kPa，两个压力脉动测点C2和C3分别位于转轮出口和导叶流道中部。测点C4处的主轴径向振动速度通过德国Polytec 多普勒激光测振仪测量，分辨率可达到0.02 (μm·s-1)/(Hz)0.5。压力脉动信号、噪声信号和主轴径向振动信号通过数据采集卡同步采集，以确保时序同步。

本文中，混流泵非线性或线性启动方式是指启动过程中叶轮转速随时间的变化规律为非线性或者线性。混流泵启动的目标转速是额定转速nr，因此在启动总时间给定后即可根据直线函数关系获得线性启动的转速上升规律如式（1）所示。非线性启动则采用了两种指数规律[24]，根据其函数图像形状将其命名为凸指数函数和凹指数函数启动规律，分别如式（2）和式（3）所示。

式中nt为启动过程中不同时刻的混流泵转速，r/min；t为启动过程中的任意时刻，s；TF为整个启动过程的总时间，s；Tna为名义加速时间[24]，s；A为无量纲指数规律常数。

3 种不同启动规律对应的转速上升曲线如图2 所示。本试验将混流泵整个启动过程的总时间TF设置为1 s[20]。在指数启动规律中，Tna取为0.13 s，指数规律常数A取为7.5，确保启动总时间达到后对应的转速为正常工作转速nr。启动试验过程中，压力脉动、噪声和主轴振动信号的采样频率统一为10.24 kHz，以确保信号的同步分析。

图2 不同启动方式的转速上升曲线Fig.2 Rotation speed rise curve of different start-up mode

2 信号处理方法

本文采用声音信号分析方法对叶轮处噪声信号进行分析。

2.1 能熵比

在混流泵启动过程的噪声信号中，既有流体噪声也存在轴承等机械部件碰撞产生的冲击噪声，但常规的时频分析方法无法分析噪声信号中冲击成分的变化趋势，也就无法从噪声信号中获悉启动过程中机械部件碰撞的严重程度。为此，本文对混流泵启动过程中的噪声信号进行了能熵比分析，通过泵段噪声信号的能熵比变化规律分析混流泵启动过程中机械碰撞、冲击的发展规律。能熵比[25]是针对时域信号的一种分析算法，其可以将信号中的信噪比提高，增强声音信号中微小冲击成分的特征。能熵比计算的过程是首先对时序信号x(n)进行消除直流分量与幅值归一化处理，然后对其中第i帧的xi(n)进行傅里叶变换后得到第k条谱线频率分量fk的能量谱为Yi(k)，然后得到每一频率分量的归一化谱概率密度函数pi(k)，则第i帧的能熵比Ri可根据式（4）～（6）进行计算：

式中N是时序信号中的数据样本量，a是调节信号第i帧能量的常数，pi(k)是第k条谱线频率分量对应的归一化谱概率密度函数，Ei是信号第i帧的能量，Hi是信号第i帧的谱熵，Ri是信号第i帧的能熵比。

除了能熵比外，在分析噪声信号的频率特性时通常引入倍频程[26]的概念。倍频程根据倍数的不同分为很多种，而其中1/3 倍频程方法得出的频段更符合人耳的听觉，其上下限频率关系如式（7）所示。

式中fu为上限频率，fl为下限频率，fc为中心频率。

各个倍频程带内的声压均方值是该频带内频谱谱线的均方值之和。本文将不同启动方式下的泵段噪声信号按1/3 倍频程谱进行了计权声压级统计以分析启动方式对噪声强度的影响规律。计权声压级计算采用A 计权，因为A 计权充分考虑了人耳可感知的不同频率噪声导致的扰动[27]。

2.2 语谱图

为提取混流泵启动过程中噪声信号的共振峰，采用语谱图[28]对噪声信号进行了分析。语谱图反映了声音信号的动态频谱特性，在语音分析中具有重要的实用价值，被称为可视语音。绘制语谱图的流程为先对语音信号进行预加重，然后对信号进行分帧并开展短时傅里叶变换得到每帧信号的频谱图，最后将每帧信号的频谱图进行旋转映射并进行拼接即可得到声音信号的语谱图。根据语谱图即可估算声音信号的共振峰。

2.3 关联性分析方法

噪声的根源包括水动力噪声源和机械噪声源，压力脉动是水泵内部主要的水动力噪声源之一，而轴系的机械振动则是水泵中的机械噪声源。在启动过程中，为了确定噪声的主要影响因素，本文应用小波偏相关方法[29]对主轴径向振动速度、压力脉动与噪声信号进行了相关性分析。

3 结果与分析

3.1 噪声的时频分析

时频特性是信号的基本特性，所以研究启动过程中噪声信号的第一步是分析其时频特性。图3 给出了3 种启动方式对应的噪声时域信号。启动过程的噪声信号为非稳态噪声信号，为对比3 种噪声信号的声压强度，对3 种噪声声压信号按Δt=0.2 s 的间隔进行信号分段峰峰值对比。

为便于分析，本文将0.4～0.6 s 时间段定义为启动中期，中期前的时间段为初期，中期后的时间段为后期。在启动初期（0～0.4 s），凸指数函数启动方式的声压峰峰值明显高于其他两种启动方式，而凹指数函数启动方式声压峰峰值最低；在启动中期（0.4～0.6 s），仍然是凸指数函数启动方式的声压峰峰值最高，其比线性启动方式的对应值高32%，比凹指数函数启动方式的对应值高28.4%；到达启动后期（0.6～1.0 s）时，两种非线性启动方式的声压峰峰值均高于线性启动方式。综合3 种启动方式的转速上升规律以及声压峰峰值的变化规律可知，启动过程中的声压峰峰值主要受转速及转速上升加速度影响，转速值及转速加速度值均与声压峰峰值呈正相关关系。

为了获知不同启动方式诱发的泵段噪声的频率特性，采用小波变换方法对泵段处的噪声信号进行了时频分析，结果如图4 所示。3 种不同启动方式下，泵段处噪声信号的高幅值区域A、区域B 和区域C 均出现在220～300 Hz 频段内，但启动方式的差异使得高幅值区域的分布呈现不同的形式。3 种启动方式中，线性启动和凸指数函数启动方式下高幅值噪声区域占据的启动时间长（均超过0.3 s），而凹指数函数启动方式下高幅值噪声区域出现的时间尺度最短（仅为0.18 s），可见凹指数函数启动方式对环境的持续性影响程度相对最小。3 种启动方式下的高幅值区域均集中在启动过程的末期，而且线性启动方式下噪声声压的最高峰峰值小于其他两种启动方式。

图4 噪声时频特性Fig.4 Time-frequency characteristic of noise

3.2 噪声能熵比分析

3 种不同启动方式下泵段处噪声信号的能熵比随时间变化规律如图5 所示。从图5 中可以看出，3 种启动方式下泵段处噪声的能熵比随时间的变化规律相似。在启动开始后的0～0.6 s 阶段，线性启动与凹指数函数启动方式下能熵比的数据标准差分别为0.061 和0.096，而凸指数函数启动方式的相应能熵比数据标准差为0.126，大于其他两种方式。由此表明0～0.6 s 时间段内线性启动和凹指数函数启动方式下能熵比的变化幅度相对较小。在启动时间刚好到达0.6 s 时，3 种启动方式下的噪声信号短时能熵比值分别达到了启动开始时的3.22（线性）、5.78（凸指数函数）和2.36 倍（凹指数函数），表明凸指数函数启动方式导致的转速快速上升引发了剧烈的机械碰撞冲击，诱发了强烈的冲击噪声。

图5 噪声信号的能熵比Fig.5 Energy entropy ratio of noise signal

从图5 还可发现，在启动后期（0.6～1.0 s），3 种启动方式对应的噪声能熵比均出现了峰值，波动剧烈，说明混流泵启动后期过高的转速也会导致主轴与轴承座、支撑架之间的碰磨愈加剧烈。综合上述不同启动方式下泵段噪声信号的能熵比分析结果可知，启动过程中过高的转速增长率和转速值都会引发强烈的机械碰撞冲击，从而产生强烈的冲击噪声。凹指数函数启动方式下的能熵比平均值为0.29，为3 种启动方式中最小值，表明该启动方式产生的冲击噪声相对最小，最有利于避免启动过程中剧烈的机械碰撞冲击。

3.3 噪声的1/3 倍频程谱

图6 为不同启动方式下泵段处噪声的1/3 倍频程谱。从图6 中可知，3 种启动方式下A 计权声压级最高值分别为72.88 dB（线性）、75.93 dB（凸指数）和75.58 dB（凹指数），它们对应的中心频率均为250 Hz。250 Hz的中心频率代表177～355 Hz 的频段范围，根据噪声频率的分类，这3 种启动方式下A 计权声压级最高的噪声均为低频噪声。在启动过程中，混流泵内部会出现复杂的流场结构，包括了进口回流、动静干涉以及转轮叶片前缘空化等流动现象，这些流动现象会形成水动力噪声源引发水动力噪声向外界传播。其中，能引发177～355 Hz 频段范围内水动力噪声源的流动现象包括转轮叶片前缘空化和动静干涉。动静干涉引发的压力脉动是水泵内部常见的偶极子声源。从混流泵启动开始至额定转速nr，动静干涉在叶轮端引发的压力脉动频率为7 倍瞬时转频，频率范围为0～210 Hz，在导叶端引发的压力脉动频率为4 倍瞬时转频，频率范围为0～120 Hz，所以动静干涉产生的压力脉动及其高次谐波会引发177～355 Hz 频段范围内的水动力噪声。具有一定规模的空泡群引起的空化噪声频率在几百赫兹左右[30]，所以叶片前缘空化形成的空泡群也具备引发中心频率为250 Hz 的水动力噪声的可能性。

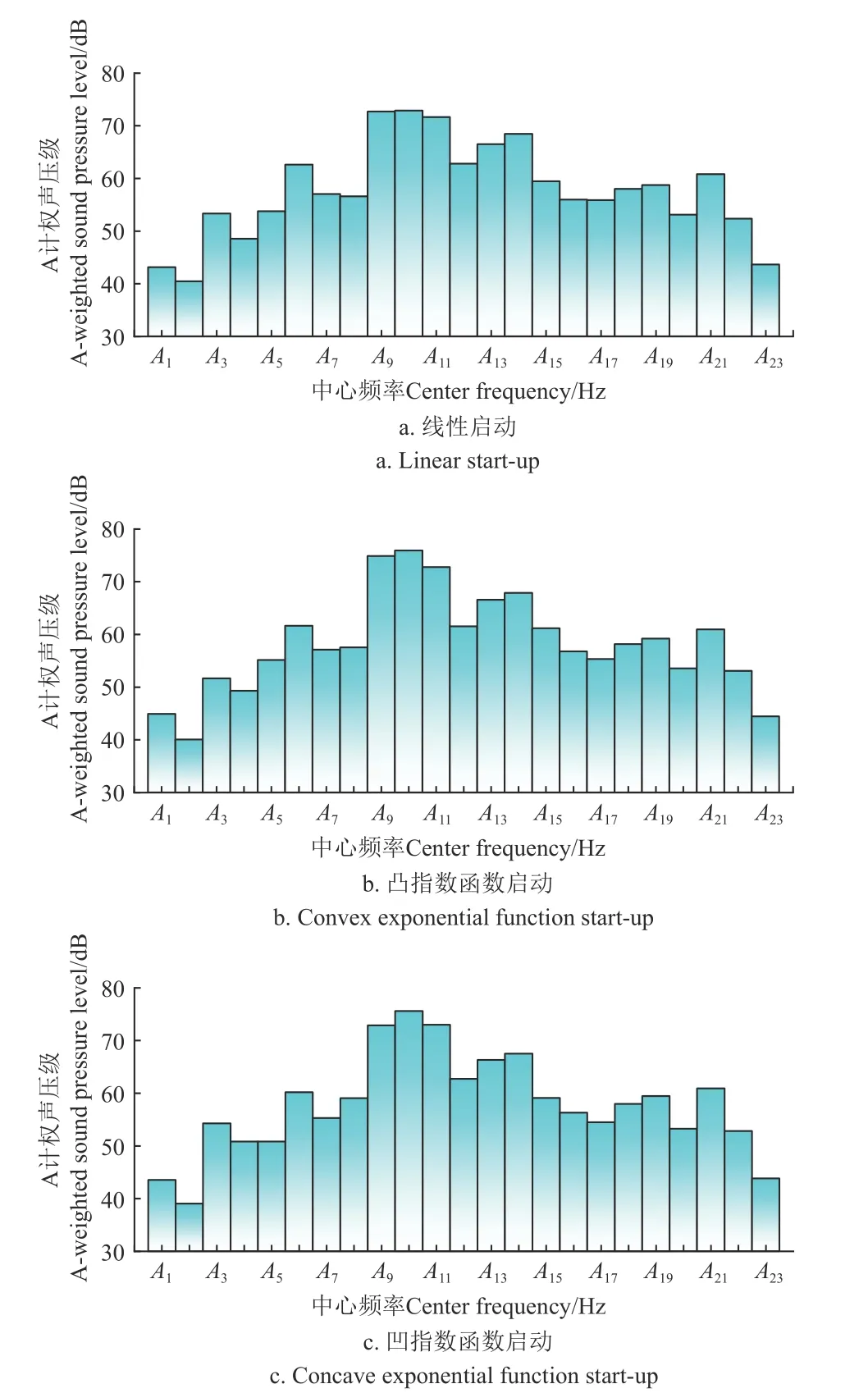
图6 噪声信号的1/3 倍频程谱Fig.6 1/3 octave band spectrum of noise signal

对不同启动方式对应的噪声总有效声压级进行了计算，线性启动对应的总有效声压级为78.7 dB，凸指数函数和凹指数函数启动对应的总有效声压级分别为80.2 和79.7 dB。可见线性启动时泵段处噪声的总有效声压级最小，而凸指数函数启动方式时最大。泵段处的噪声主要为流致噪声[31]，而压力脉动是流致噪声的主要根源之一。统计启动过程中两个压力脉动测点的信号能量之和，线性启动方式对应的压力脉动信号总能量为4.03×1011Pa2·s，而凸指数函数启动和凹指数函数启动对应的压力脉动信号总能量则分别为5.63×1011和4.58×1011Pa2·s。凸指数函数启动方式中压力脉动信号的总能量最高，表明其流致噪声源的能量大，因此辐射出的噪声有效声压值高，而线性启动方式下压力脉动信号的总能量最小，相应的外场辐射噪声有效声压值就低，所以启动方式引发的泵内压力脉动能量的变化是影响启动过程中泵段外场辐射噪声声压值的主要原因之一。

为了更详细地对比线性启动和两种非线性启动方式的噪声声压级差异，计算不同中心频率下非线性启动相对线性启动的A 计权声压级变化率，结果如图7 所示。

图7 凸、凹指数启动分别相对线性启动的噪声声压变化率Fig.7 Change rate of noise sound pressure between convex and concave exponential start-up and linear start-up respectively

从图7 的整体趋势来看，在低频段内（＜400 Hz）线性启动与非线性启动的差异最为明显。在中心频率为40、80、100 及125 Hz 的频段处，凹指数函数启动方式的噪声声压级值均优于线性启动，其声压级值均比线性启动的声压级值降低了3%以上。其中，在中心频率80 Hz的频段处，凹指数函数启动方式对噪声声压级值的改善程度最高，其声压级值比线性启动低了5.8%。在中频段（400～1000 Hz），凹指数函数启动的声压级值全面优于其他两种启动方式，但其在高频段只有中心频率1 250 Hz频段处的声压级优于其他两者。综合上述分析可知，相比于线性启动方式，采用凹指数函数启动可以改善启动过程中的中频段噪声声压级和部分低频段噪声声压级。

3.4 噪声的语谱图

图8 所示为混流泵不同启动方式下泵段处噪声信号的宽带语谱图，图中每个纵条纹称为声纹，声纹颜色的深浅代表信号能量大小。

图8 不同启动方式下的噪声语谱图Fig.8 Noise spectrogram of different start-up modes

图8 中黑框占据的时间长度为噪声高能量分布的时间跨度，线性、凸指数函数、凹指数函数启动的时间跨度为分别为0.4、0.25 以及0.07 s。由此可见，虽然线性启动过程中泵段处噪声的最高能量值比两种非线性启动方式小，但其高能量分布占据的时间跨度长。从图8中还可发现，线性启动和凸指数函数启动均存在两个共振峰，而凹指数函数启动仅有一个共振峰，表明线性启动和凸指数函数启动过程中诱发了两次谐振，而凹指数函数启动仅有一次。因此，针对本次试验用的混流泵，凹指数函数启动比另外两种启动方式诱发失稳的概率更低。

从图8 可知，不管是线性启动还是非线性启动，其高能量频带均集中在200～315 Hz，这与图6 中高声压值出现的频段位置一致。此外，在语谱图中可以发现，当启动时间到达0.6 s 之后，深颜色声纹的占比增加，表明噪声信号的能量出现较大幅度的提升，这与图4 中的声压幅值变化趋势一致。因为当启动时间到达0.6 s 之后，声压的幅值开始明显增加，所以噪声的能量也必然提升。

3.5 噪声的关联因素分析

根据小波偏相关方法对主轴振动、压力脉动和噪声信号进行了相关性分析。分析结果表明，三种启动方式下的主轴径向振动速度、压力脉动与噪声信号的相干谱具有相似性，限于篇幅，本文只展示了线性启动下的分析结果，如图9 所示。

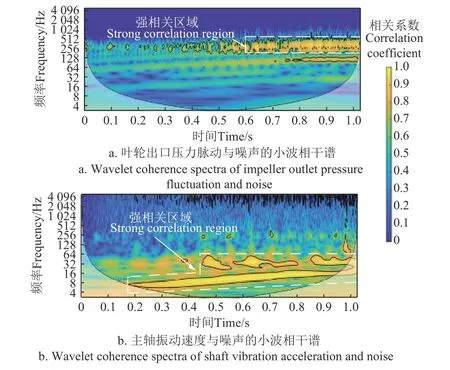
图9 小波相干谱Fig.9 Wavelet coherence spectrum

根据小波偏相关的分析结果，叶轮出口处的压力脉动与叶轮噪声的偏相干性主要集中在256 Hz 的频段处，并且强相干区域也处于启动时间0.6 s 后。而主轴径向振动速度与噪声的相干性频段则集中在8～32 Hz 的低频段处。由此可见，中心频率为250 Hz 处的高声压值主要由叶轮出口处压力脉动所导致，而该处的压力脉动以动静干涉压力脉动为主，这也验证了前文中认为动静干涉压力脉动是中心频率250 Hz 频段处高声压值产生原因之一的推论。主轴径向振动则主要影响8～32 Hz 极低频段内噪声，但这部分频段内的噪声声压并不是泵段处噪声声压的主要成分。

4 结论

本文基于试验测试方法对混流泵启动过程中泵段处的噪声特性进行了研究，分析了凸指数函数、凹指数函数和线性启动方式对泵段处噪声特性的影响，主要结论如下：

1）对于本文研究的3 种启动方式，启动过程中泵段处噪声声压的高幅值区域均集中在启动过程末期。3 种启动方式中，凹指数函数启动方式下高幅值噪声区域出现的时间仅为0.18 s，对环境的持续性影响程度最小。

2）3 种启动方式下，泵段处噪声的最高A 计权声压级均位于中心频率为250 Hz 的频段处。凹指数函数启动方式有利于避免启动过程中剧烈的机械碰撞冲击，其诱发混流泵启动过程失稳的概率在3 种启动方式中相对最低。与线性启动方式相比，凹指数函数启动能全面改善中频段（400～1 000 Hz）噪声声压级和部分低频段声压级，其中最大改善程度为A 计权声压级降低5.8%，出现在中心频率80 Hz 的频段处。

3）启动过程中，泵叶轮出口压力脉动是影响泵段处噪声主声压级（中心频率250 Hz）的主要因素，主轴径向振动只影响极低频段处的噪声。