基于群智慧对选择算法的分布式一致性时间同步方法*

周华勇，陈珍萍

(苏州科技大学电子与信息工程学院，江苏 苏州 215009)

在工业化和信息化深度融合的发展趋势下，凭借低功耗、低成本、易部署和自适应的优势，无线传感器网络(Wireless Sensor Networks，WSN)成为了工业物联网的关键技术，引起了广泛的关注[1]。 环境的不可确定性对于无线传感网络的实时性、准确性和可靠性提出了较高的要求。 如今的工业无线标准大部分都是基于介质访问层控制机制，如时分多址技术，其允许多个设备通过将传输周期分成多个时隙来共享对公共通信信道的访问。 时间同步是无线传感器网络中不可缺少的一部分。 无线传感器网络中的每个传感器都是独立工作的，都有自己的时钟。即使传感器时钟的初始状态被调整得很完美，在实际的工作过程中，由于环境、温度、硬件等一系列因素的影响，不同的时钟可能会随着时间而产生不同的误差[2]。 当传感器节点的时钟需要通过与全球定位系统(Global Positioning System，GPS)卫星或网络时间协议[3](Network Time Protocol，NTP)互联网上的时间服务器来同步时，无线传感器网络中一般装备了大量从节点来与一些主时间节点同步。 为了做到这一点，需要分布式网络时钟同步协议，通过该协议可读取传感器的时钟，并将读数传输到其他传感器节点，进而根据需要调整每个传感器节点的时钟。 在这种分布式同步方法中，参与设备以规定的间隔与它们选择的基准交换定时信息，并相应地调整它们的逻辑时钟。 由于实际上时钟的设置精度有限，且同一节点运行的不同时间或同一运行时间的不同节点，它们时钟的晶振频率不同，因此，分布式时钟必须定期同步。

时间同步是无线传感器网络的一个重要问题，因为许多协作任务都需要时间协调。 无线传感器网络的时间同步协议发展至今，针对不同的应用分别提出了很多种集中式和分布式同步协议和算法。

集中式同步协议，例如:时间传输协议(Time Transfer Protocol，TTP)[3]是一个节点用来将它的时钟时间传送给另一个目标节点。 目标节点通过使用消息时间戳和消息延迟统计来估计源节点中的时间，而无需任何反馈响应或成对同步。 利用了广播媒体的固有特性(一个节点向单个广播区域内的所有节点发送定时信标)。 无线传感器网络中最流行的时钟同步协议之一参考广播同步协议(Reference Broadcast Synchronization，RBS)[4]就是基于相同的思想提出的，但允许协议拓展到多个域。 RBS 是基于事后接收器-接收器同步方法，在无线基站中，一个节点向两个或多个相邻节点发送参考广播消息，相邻节点在接收到广播消息时记录自己的本地时钟。 在收集了一些信息之后，节点交换它们的观测值，并且使用线性回归方法来估计它们的相对时钟偏移和偏斜。 传感器网络的定时同步协议(Timingsync Protocol for Sensor Networks，TPSN)[5]是一种传统的发送方-接收方协议，它假定有两个操作阶段:级别发现阶段和同步阶段。 在级别发现阶段，WSN以生成树的形式组织，通过仅调整其时钟偏移，使用发送端-接收端机制沿着层次结构的分支进行成对同步，使每个节点能够与其父节点(位于相邻上层的节点)同步。 在无线传感器网络的分层结构中，当有新节点加入或有节点损坏导致拓扑结构变化时，集中式同步协议必须要处理[6]。 因此，集中式同步协议的设计往往计算复杂度高，鲁棒性差，能耗大。 而且，集中式同步协议还会有累计误差和不平衡的同步精度等缺点。

分布式同步协议一般基于一致性算法，如全局时钟同步(Global Clock Synchronization，GCS)[7]、分布式时间同步协议(Distributed Time Synchronization Protocol，DTSP)[8]和一致性时钟同步(Consensus Clock Synchronization，CCS)[9]。 分布式同步协议利用本地信息不依赖于主节点或参考时钟，因此可以提高可伸缩性、负载平衡以及鲁棒性。 但分布式同步协议的通信成本高，收敛时间长，特别是在大型或稀疏的无线传感器网络中。 同时由于其不与外部时钟源同步，在网络被分割成独立的信息孤岛后，需要后续某种形式的时间同步处理，以能够融合每个独立区域的时间信息[10]。

为了解决以上问题，本文将基于群智慧对选择算法(Group-wise Pair selection Algorithm，GPA)的分簇技术和分布式一致性时间同步技术结合，提出了一种应用于大规模无线传感器网络的时间同步方法。 本文主要贡献为:①基于GPA 算法对一致性算法的拓扑结构进行改进，使得时间同步算法能够适应各种环境；②引入双向信息交换模型，对网络中由一致性算法形成的各信息孤岛进行有效的数据融合，使得网络规模能够有较好的可拓展性；③采用分簇的拓扑结构，减少节点之间信息交换的数据量，从而减少了能源消耗，延长了网络的生命周期。

1 节点时钟模型

本节我们建立无线传感器网络时钟的数学模型。对网络中的节点i，建立其一阶时间模型，具体为:

式中:ωi和φi分别是节点i的频率偏移和相位偏移。ωi受节点晶振精度、环境温度、压力和供电电压等因素影响，φi受节点初始上电时刻影响。 虽然ωi和φi无法直接计算，但可以通过两个节点的相对本地时钟信息进行估计。 对于节点i，我们可以解得，将其带入节点j的^τj(t)中，可以得到:

需要注意的是，考虑到节点的其他功能，如定时采样、操作系统的时钟节拍中断等，需要根据的连续记时来进行，一般情况下不允许对进行修改。 在无线传感网络中，通常想把通信范围内所有的节点时钟都同步到一个虚拟时钟，即:

式中:ωv和φv分别是虚拟参考时钟的频率偏移和相位偏移。 对于虚拟参考时钟，它并不是预先设定的，它的可调参数值(ωv，φv)并不固定，最后能够使所有的节点时钟收敛到一个共同的虚拟参考时钟。 通过MAC 层时间戳技术，本文假设本地时间的读取和包传输是瞬时的[11]。

网络中每个节点i的本地时钟都是根据其本地时钟的线性函数估计值表示，即:

式中:N为无线传感网络中的总结点数。作为一个虚拟时钟，并不是一个物理时钟。 将式(1)带入式(4)有:

又由式(5)，当t→∞时有:

由式(7)、式(8)可以得到，节点在同步时应该获得的补偿参数为＾ωi和＾φi，通过这两个参数的补偿，可让节点i时间能够与虚拟时间同步一致。

2 基于GPA 算法的一致性时间同步

在本文提出的方案中，不是试图与外部的参考时间(如世界协调时钟UTC)同步，而是在网络的内部就时间和频率的偏斜速率达成一致。 无线传感器网络在每一次时间同步后，更新每个节点的补偿参数，随着一轮一轮的同步，网络中所有节点的时间收敛到一致，具体如式(5)所示。

时间同步过程为:在网络拓扑生成阶段，本文引入了一种基于GPA 算法的拓扑结构生成方案，从汇聚节点开始按照通信半径将网络划分为一个一个的簇；对簇内节点基于一致性理论实现同步，而簇与簇之间的时间同步则通过簇首间的双向信息时间同步实现。

2.1 基于GPA 算法的网络拓扑生成

现有一致性时间同步协议大都假设底层传感器网络通信图是强连通的，即网络中存在从任意节点到任意节点的通信路径[12]。 然而受通信环境等因素影响，该假设在现实中难以得到保证。 由于建筑、山体等障碍物的阻挡，会影响节点信号的传输，导致某些节点可能无法与通信范围内的其他节点通信；甚至有时因为天气、电池能耗等因素导致节点损坏，无法正常工作。 这些都会导致网络拓扑的改变，从而影响时间同步方案的运行。

本文所引入的拓扑生成方案能够在拓扑发生改变时，使用较少的信息传输数据量重新生成网络拓扑。 在WSN 拓扑生成阶段，假设网络中的节点为静态节点，且具有唯一ID 号；假设所有感知节点初始能量相同且不能补充。 记网络中的节点为Sk(k＝1，2，…，N)，其中网关节点记为S1。 拓扑生成包括两个过程:网络拓扑结构生成阶段和基于GPA 的成对同步(Pairwise Synchronization，PS)向量生成阶段。生成的网络拓扑结构如图1 所示。

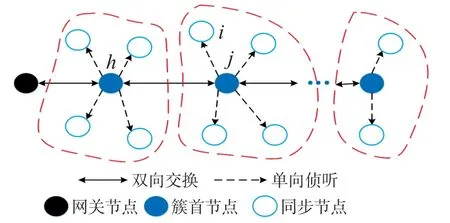
图1 网络拓扑结构

在网络拓扑结构生成阶段，网关节点S1周期性广播级别数据包(带有自身级别号和ID 号)，其所有单跳邻居节点接收到数据包后则分配一个比发送数据包的节点高一级的级别，同时这些节点也会广播发送同样类似的数据包，依次类推，直到网络中所有节点都获得级别号。 节点在分配完级别号后会丢弃其他的级别发现数据包，以防止冲突。

在基于GPA 的PS 向量生成阶段，拥有同一个级别号的节点作为一个簇，在每一个簇内的节点向其他簇内的节点广播连接发现数据包，若该簇中其他节点接收到信息包，则发回应答信号，若收到属于其他簇的节点的连接发现数据包也会将其丢弃。 节点标记节点间连通值Md，n＝1，否则Md，n＝0；该群中同时与Sd和Sk节点连通的节点个数为，与该簇内节点连通最多的节点号＾d＝arg maxNd，k。 节点S＾d可以作为两个簇之间进行时间同步的簇首节点，即PS 节点。

2.2 同步信息传输模型和簇首节点间成对同步

由于一致性时间同步方法无法实现独立区域之间的同步进而实现其信息融合，本文在生成的网络拓扑结构基础上引入双向信息交换同步机制。 考虑到节点h和j双向信息交换时，其共同通信范围内的节点i可以通过单向侦听方式获取信息包，基于双向交换-单向侦听机制实现同步信息的传输，具体如图2 所示。 图2 中，节点h与j分别在T1，1和T3，1时刻向对方传输信息包syn(包含有节点j的ID和T1，1)和ack(包含有节点h的ID 和T3，1)时，syn中包含有一次信息交换后，节点j获取的时间信息{T1，1，T2，1，T3，1，T4，1}。

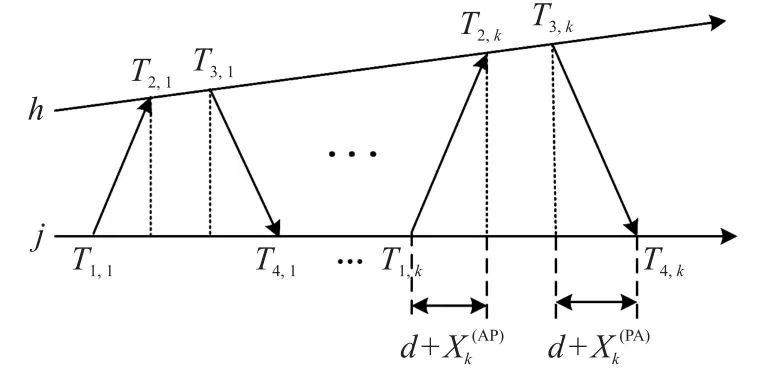
图2 同步信息双向传输

假设两个节点之间时钟的相位偏移为φ，相对斜率为ω。 如图2 所示，节点j在T1，1时刻发送时间同步请求包，节点h在T2，1时刻收到数据包，在T3，1时刻返回包含节点h时间信息的数据包，节点j在T4，1时刻收到，根据数据包中节点h的时钟信息对本地时钟做出调整。 节点j在同步过程中不断重复此操作直到达到符合要求的精度[13-14]。 所有数据包的发送与接收时刻均以该节点的虚拟时钟为基准。数据包中包含发送节点时间戳的值、识别码、节点的级别以及身份。 则T2，k和T3，k可分别表示为:

式中:d为一个节点到另一个节点的固定延迟，由于分组通常具有相同的长度和数据传输速率，这导致节点间拥有相似的发送和接收时间，且传播时间和节点间的距离保持不变，所以在这里假设d保持不变；、Y(khj)为可变延迟，本文中，X(kjh)、Y(khj)被假设为均值为0，方差为σ2的独立同分布的高斯随机变量；φ(jh)、φ(hj)、ω(jh)和ω(hj)分别表示节点A相对于节点P的时钟偏移和时钟偏斜，且φ(jh)＝φ(hj)、ω(jh)＝ω(hj)。

运用极大似然估计的方法[15]，可以计算其相位偏移和频率偏移，具体为:

2.3 基于一致性理论的簇内节点时间同步

下面来介绍簇内其他节点关于簇首节点的相对频偏和相偏的估计和补偿方法。 图1 中，簇内节点i与其簇首节点j的相对频偏可以用ωij来估计，节点i在自己本地时间(t1)接收到来自节点j的广播包中存储的本地时间(t1)，并将记录在存储器中。 由于这里使用的是MAC 层时间戳，所以假设的读数是瞬时值。 同理，当节点i从节点j接收到一个新的数据包时，就会得到一组新的数据。 则相对频偏ωij的估计可表示为:

设tk为更新时刻，初始值为ωij(0)＝ω(0)。 又由于不考虑两个采样时间t1和t2。则有:

当k→∞时，且0＜ρ＜1，就可得到精确估计值。其中参数ρ用于调整收敛速度(ρ→0)和噪声抗干扰(ρ→1)之间的平衡。 该算法对于内存的需求很小，每个节点i只需存储相对频偏估计ωij和本地时钟对。

对于基于一致性理论的簇内时间同步而言，其主要思想是一种基于簇内信息交换的分布式共识算法，即每一个节点都会保留自己对全局变量的估计，并通过相对于其邻居的估计求平均值来更新其值。在文献[16]的基础上，本文采用一致性理论进行节点虚拟时钟频率的迭代更新，具体为:

式中:ρ1∈(0，1)为调整参数，是的更新值为节点j的虚拟时钟偏差，每个节点的初始条件为(0)＝1。

在采用了频率偏移估计补偿后，仍需估计出簇内节点i和簇首节点j间的相对相位偏差，并进行补偿。 根据式(6)，可以表示出节点i的虚拟时钟估计，即:

本文选用一致性算法来更新虚拟时钟偏移量，根据式(4)有:

式中:ρ2∈(0，1)为调谐参数，和是同一时刻计算的值，为的更新值。

初始条件为(0)＝1，ρ1∈(0，1)，ρ2∈(0，1)，对于和的两个更新方程，假设对于所有节点i和任意时间t存在ωv＞0 使得ωv＝(t)ωi。 并且假设存在T＞0 使得网络中通信范围内的每个节点在任意长度为T的时间窗口中至少向其邻居发送一次本地虚拟时钟参数。 则有:

也即簇内节点i 同步到簇首节点j。

3 数值仿真结果与分析

本节将在MATLAB 仿真平台上进行本文所提基于GPA 算法的一致性时间同步方法有效性验证。

3.1 拓扑结构的生成

为了保证网络能够至少生成一个簇，将100 个仿真节点(其中一个为网关节点)随机布置在一个400 m×25 m 的矩形区域内，设置节点的通信半径为25 m。 在MATLAB 仿真平台中，模拟生成了节点的拓扑结构以及通信情况如图3 和图4 所示。

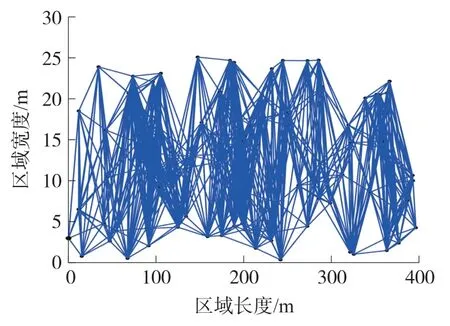
图3 初始网络拓扑

图4 基于GPA 算法的网络拓扑

图3 中坐标为(0，3)的实心点表示网关节点，其他实心点表示网络中的传感器节点，实线表示节点间的通信，图4 中直径较大的实心点表示网关节点或簇首节点(网关节点也可作为簇首节点)，直径较小的实心点表示簇内的普通节点，虚线表示簇首节点与簇内节点和其他簇首节点、以及簇内节点之间的通信。

表1 为几种拓扑生成方法的数据传输量对比。从表1 中可以看出，不同时间同步协议在完成时间同步时传输的数据包数量对比，因此与TPSN 算法和RBS 算法相比，本文所提方法所需的信息交换数量大幅度降低；与FTSP 算法相比信息交换数量也有一定程度的减少。 因此，本文所提拓扑构建方案能够有效减少节点间信息传输的数据量，从而减少节点的能量消耗。

表1 拓扑生成数据传输量对比

3.2 一致性时间同步方法仿真

在图4 所示的拓扑结构上进行本文所提一致性算法仿真。 随机选取其中一个包含10 个节点的簇进行一致性时间同步方法的仿真。 根据文献[17]，设置同步周期T＝100 s，ρ＝ρ1＝ρ2＝0.6，节点初始时钟频率偏移从[0.9，1.1]中随机选取。

节点按照式(1)所示时间模型进行迭代，所得本地时钟迭代曲线如图5 所示。

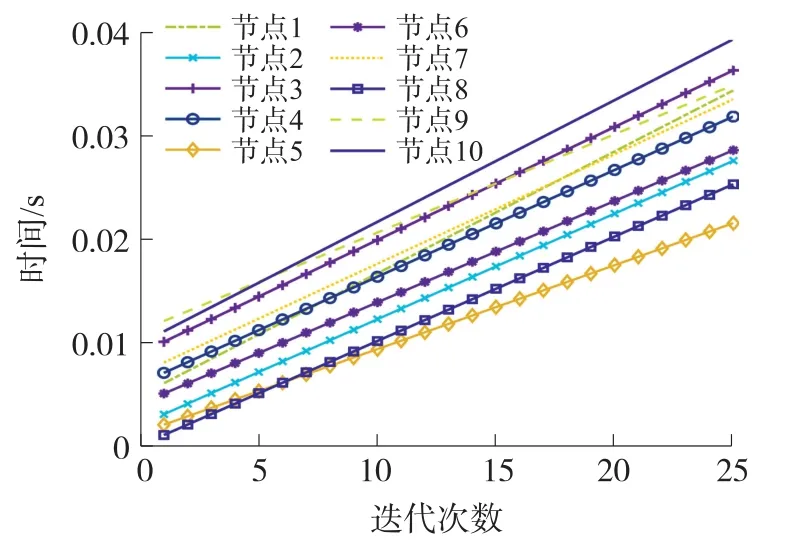
图5 无时钟调整下本地时钟迭代曲线

从图5 可以看出，在没有算法纠正的情况下，节点只会按照自己的本地时钟计时，无线传感器网络中的各节点之间时间都会存在误差，其中2 号节点和5 号节点的初始值相差0.009 s，而迭代了25 次后，这两节点之间的误差就达到了0.017 4 s，增长了近一倍。 因此，有必要采取方案对无线传感器网络进行时间同步。

根据式(15)和式(17)的方法进行节点相偏和频偏的估计、补偿，得到图6 和图7 所示的节点虚拟频偏估计补偿和虚拟相偏估计补偿曲线。 从图6 和图7可以看出，任一节点与其他节点的频偏速率之比，其比值恒定，表示节点间的频率偏斜率一致，即节点间的频偏能够保持相对一致；在进行偏移的补偿迭代后，其值基本上能按照预期收敛于某一恒定值。

图6 节点的频偏估计补偿

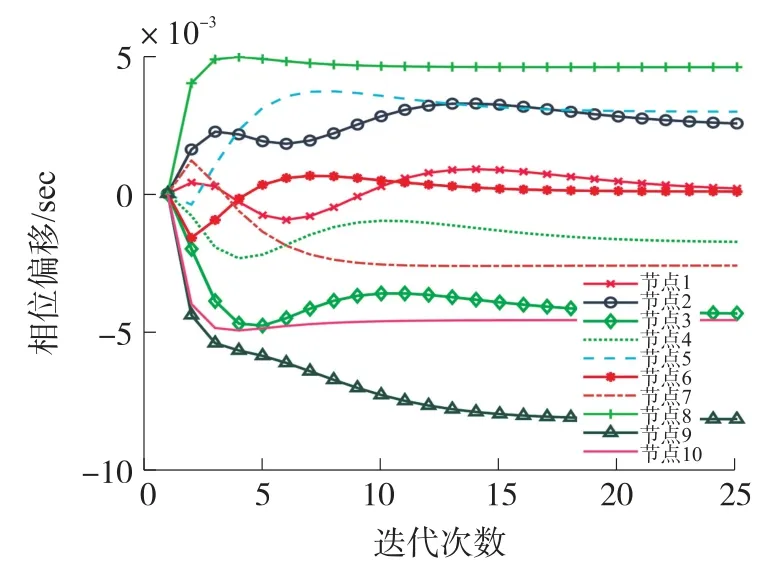
图7 节点的相偏估计补偿

根据频率偏移和相位偏移的估计值，按照式(3)对簇内节点进行时钟调整，得到图8 所示的节点虚拟时钟迭代曲线，以及图9 所示的虚拟时钟平均值的误差百分比迭代曲线，其中虚拟时钟平均值的百分比定义为为虚拟时钟的平均值)。 从图8和图9 可以看出，随着同步迭代次数的增加，节点的虚拟时钟能够趋于一致同步，节点的偏差最大为31 μs，且虚拟时钟瞬时平均值的误差百分比也会越来越小，即簇内节点的虚拟时钟偏差达到一致。

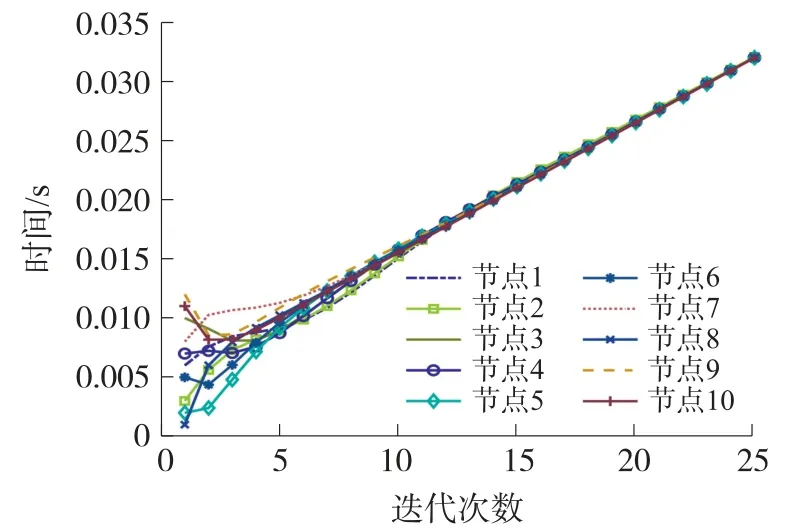
图8 节点的虚拟时钟

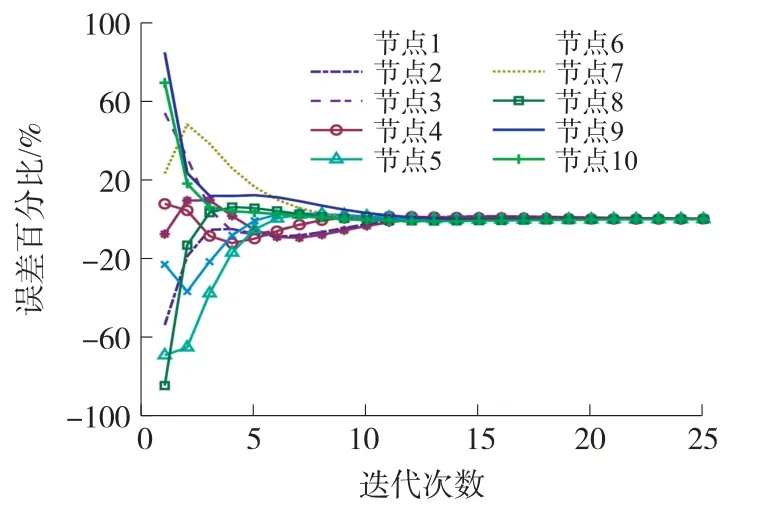
图9 虚拟时钟瞬时平均值的误差百分比

3.3 多跳网络的时间同步算法对比

本文进行了CCS(不分簇的一致性时间同步方法)、DTSP(分布式时间同步方法)和本文同步方法的同步速度对比仿真实验。 从算法时间复杂度的角度分析，时间同步算法都是节点根据接收的邻居节点发送的时钟信息运行的，其时间复杂度与节点间时钟信息交换的次数相关。 在簇内利用一致性时间同步方法的时间复杂度为O(n1)，n1为簇内节点交换时钟信息的次数；簇间利用双向信息交换机制的时间复杂度为O(n2)，n2为簇首节点交换时钟信息的次数；采用不分簇时间同步方案的时间复杂度为O(n3)，n3表示全网节点交换时钟信息的次数。 采用本文时间同步方案不需要全网所有节点之间互相通信，因此减少了时钟信息的交换次数，降低了时间复杂度，即O(n1)＋O(n2)＜O(n3)。

图10 给出了同步速度对比结果，从图10 可以看出，与另外两种时间同步方法相比，本文所提方法节点的虚拟时钟平均误差百分比曲线收敛得更快，在节点数N＝100 的网络规模下，本文方法相较于CCS 和DTSP 时间同步算法能够在更少的迭代次数基础上达到有效收敛，节点的同步误差最大为32.1 μs，说明本文所提出的方案在满足较大规模的无线传感网络时间同步的基础上，比不分簇的一致性时间同步方法具有更好的同步性能。

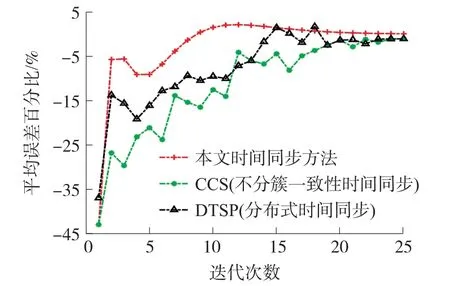
图10 同步速度仿真对比结果

4 总结

结合GPA 算法的拓扑结构以及节点间双向时间同步的特点，提出了一种改进的一致性时间同步方案，并仿真分析了它的可行性。 本文基于GPA 算法将大规模网络进行分簇，并通过一致性算法进行簇内节点的时间同步，同时利用双向信息交换时间同步实现独立的一致性时间同步区域间的时间信息融合同步。 仿真实验结果表明，本文的时间同步方法能够有效提高无线传感器网络的时间同步收敛速度，减少节点间的通信数据包数量。

在实际的网络环境中可能还有通信噪声的影响，今后的工作还会考虑通信噪声影响下的一致性时间同步。