低成本惯性传感器的信号增强与手势识别*
2023-10-08杨森乔王一峰
杨森乔,王一峰,赵 毅
(哈尔滨工业大学(深圳)理学院,广东 深圳 518055)
伴随着增强现实(Augmented Reality,AR)、虚拟现实(Virtual Reality,VR)以及元宇宙的兴起与发展,通过手势识别进行人机交互已经成为智能终端产业的热点和必备要素[1-4]。 由于惯性传感器在数据采集过程不受光线、遮挡、噪音等外界环境的影响,因此基于惯性传感器的手势识别任务具有非常广阔的应用前景[5]。 其中低成本惯性传感器具有体积小,功耗低,可穿戴性强的优势,可以广泛应用于各种生活场景[6-7],但同时由于其成本低廉,其品质和性能参差不齐,所采集的IMU 数据中往往包含有严重的误差干扰,进而造成轨迹还原、运动追踪、手势识别等任务的效果较差[8-9]。 近年来,学者们对于惯性传感器手势识别任务的研究往往集中在对特定手势进行分类等简单功能上,且其识别方法无法适应于不同的手势运动习惯,扩展性较差[10-11]。因此,如何对低成本惯性传感器进行信号增强,从其所包含的有限信息中提取有效特征,以进行高精度的手势识别,成为了亟待解决的技术问题。
IMU 信号作为一种时间序列数据,早期人们主要通过统计学方法对其进行分析处理,即通过提取时间序列的偏度峰度,均值方差等时域特征,并对时间序列进行快速傅里叶变换(Fast Fourier Transform,FFT)提取其频域特征[12]。 然而随着数据量的增大,信号的非平稳性越来越强,FFT 作为一种全局性的处理方法,无法对非平稳信号进行处理,且处理结果无法反映出信号在局部区域的频域信息。 为此,人们提出利用小波变换(Wavelet Transform,WT)对信号进行处理,以期实现对时间序列的局部化分析,并且可以对多频率的信号进行多尺度、多分辨率的处理,使得特征处理更加细致[13]。 由于上述方法仅对时间序列单一范式进行时频分析并提取特征,而忽略了数据之间的结构信息,进而导致了在对金融数据[14]、生理信号[15]、多相流[16]等复杂系统的多元时间序列进行分析时,往往无法得到较好的结果。为此,学者们通过将时间序列转换为复杂网络的方式,提取复杂系统中的拓扑特征,并将其与时频特征相结合,以实现对复杂系统更完备的分析。
为了将时间序列转换为复杂网络,Lacasa等[17-18]提出了可视图、水平可视图等时间序列-复杂网络转换策略。 然而,上述方法虽然较为简单,但由于其只考虑节点间数值排序大小作为复杂网络连接的标准,因此极易受到异常数据和随机误差的干扰。 为此,人们提出了将相空间的回归矩阵对应为邻接矩阵的递归网络策略[19],通过将原始序列进行相空间重构,并去除其伪近邻点,有效避免了随机误差对复杂网络转换以及相应网络拓扑特征提取的干扰。 同时,我们的前期工作也证明了基于回归图的转换方法,时间序列可以等价地转换到复杂网络结构,其中的原始距离信息保持不变[20]。
此外,低成本IMU 虽然便于规模化应用,但不可避免地包含有严重的随机误差[21]。 为了从信息量有限的低成本IMU 数据中提取出有效特征,人们常通过傅里叶变换[22],卡尔曼滤波[23]等方法对原始IMU 数据进行信号增强。 然而正如前文所述,傅里叶变换作为一种全局的积分变换,无法体现出信号的瞬时频率随时间的变化情况,且对非平稳信号的处理效果也并不理想,而基于其改进的短时傅里叶变换[24]虽然可以反映局部信息,但其分辨率固定,无法对时间序列进行精细化处理。 而卡尔曼滤波主要适用于线性系统,在实际应用中受到多方面的限制。 而近年来,基于经验模态分解(Empirical Mode Decomposition,EMD)的信号增强取得了较多成果[25]。 EMD 可以基于局部特征将时间序列分解为多个本征模态函数(Intrinsic Mode Function,IMF),并对各个IMF 进行精细化处理,因此EMD 成为了一种常用的非线性、非平稳信号的处理方法。张翀[26]将EMD 分解得到的各IMF 分量分别设置阈值函数以达到减少随机误差的目的,然而其处理方法会导致高阶IMF 分量中有效信息的大量损失。而王亚娟等[27]通过样本熵构建阈值对IMF 进行处理,虽然能较准确地区分语义信息与随机误差的界限,然而其方法仅在地质信号上有较好的表现,在生理信号、IMU 信号等领域表现较差,其泛化能力较弱。
因此,针对低成本IMU 数据包含大量随机误差这一问题,本文提出了一种“经验模态分解-复杂网络-小波变换”三阶段信号增强策略。 该策略借助复杂网络的确定性指标对低成本IMU 数据通过经验模态分解得到的IMF 分量进行随机性强弱的评估,然后利用小波变换对随机误差进行有效控制,以实现低成本IMU 的信号增强。 此外,由于复杂网络的拓扑特征不易受时频域上随机误差的干扰,本文在IMU 运动识别任务中,将时间序列的时频特征与反映运动过程动力学性质的复杂网络特征相结合,并构建随机森林进行分类。 在不同用户运动习惯各异、IMU 型号多样且成本低廉的条件下,本文实现了对62 种三维手势动作的高精度识别。
最后,本文对比了机器学习模型与深度学习模型的手势识别精度。 可以发现,相比于深度学习,机器学习不仅具有更强的解释性,且在特征选择合适的情况下,机器学习的识别精度可以超过深度学习模型。 进一步体现了复杂网络拓扑特征在运动状态识别、时间序列分析领域的重要价值,为模式识别提供了新的参考。
1 低成本惯性传感器的信号增强策略
本文首先对IMU 数据进行经验模态分解,并将得到的多分辨率IMF 分别转换为复杂网络递归图的形式,以借助复杂网络的确定性指标对各个IMF分量的随机性进行评估。 进而根据随机性强弱,对含较多随机误差的IMF,利用小波阈值降噪策略进行处理。 最终,将处理后的IMF 分量重构回原始IMU 信号,以实现对低成本惯性传感器的信号增强。 本文提出的“经验模态分解-复杂网络-小波变换”(EMD-CN-WT)三阶段信号增强策略的具体流程如图1 所示。

图1 三阶段信号增强策略流程图
1.1 经验模态分解
经验模态分解常用于处理非平稳信号。 它将原始IMU 信号分解为一系列包含局部特征的本征模态函数,并通过对各本征模态函数设置滤波器、阈值函数等,以实现对原始数据信号增强的效果。
对于原始时间序列x(t)经验模态分解的具体步骤如下[28]:
①确定原始时间序列x(t)的局部极大值和极小值点,并通过插值法拟合得到时间序列的上包络线xmax(t)和下包络线xmin(t)。
②计算时间序列上下包络线xmax(t)和xmin(t)的均值m1(t):
③原始时间序列x(t)减去均值m1(t)得到经处理后的时间序列h1(t)
④检验h1(t)是否满足成为IMF 的条件,若不满足,将h1(t)作为原始时间序列,重复上述过程,直到其满足条件;若满足,将h1(t)视为新的IMF 分量,并利用原始时间序列减去该IMF 分量,计算出残差r1(t),即:
⑤再将残差r1(t)作为原始时间序列重复上述过程,直到残差仅为趋势项(极值点个数小于两个)时停止,并输出全部的N个IMF 分量以及最后的残差Res(t)。
通过上述分解即可得到:
式中:每个IMF 分量需要满足两个条件:①IMF 分量中极值点个数与过零点个数,相差不能超过1;②在任意点,通过极大值和极小值构成的上下包络线的均值必须为零。
对低成本IMU 数据进行经验模态分解后,由于惯性传感器在数据采集过程包含有大量的随机误差,因此需要确定各IMF 分量中随机误差的大小,以对其进行精细化处理。 由于复杂网络的拓扑学特征,往往不易受时频域上随机误差的干扰,且复杂网络的相关统计指标可以很好地对原始数据的随机性进行评估,进而反映出各IMF 中包含随机误差的大小。 因此本文通过将时间序列转换为复杂网络,并借助其确定性指标对各IMF 中随机误差大小进行评估。
1.2 递归图确定性
递归图是一种特殊的复杂网络表示形式,可以通过观察递归图中递归点的分布情况,研究复杂系统中所隐含的随机性和确定性等信息。 其中确定性是递归图量化分析中的常用指标,其定义为[29]:
式中:P(l)表示的是长度等于l的对角线结构分布概率,lmin表示最小的对角线长度,故确定性的取值范围为0 到1 之间。
如图2(a)所示,在随机时间序列转换成的递归图中,递归点的分布杂乱无章,呈现明显的随机特征。此时,我们可以计算得到它的DET 值是0.08。 而如图2(b)所示,将正弦信号转换为递归图,可以发现该图中递归点的分布有着明显规律:递归点构成了与主对角线平行的线段。 因此,由正弦信号转换成的递归图确定性更强,随机性更弱,其DET 值为0.97。

图2 随机时间序列和周期时间序列转换为递归图
通过递归图的确定性,可以很好地衡量各IMF分量中随机误差的大小。 在去除IMF 分量中随机误差时,为避免各IMF 中包含的语义信息受到损失,本文通过小波阈值降噪,在多分辨率多尺度上对含有较大随机误差的IMF 进行降噪处理。
1.3 小波阈值降噪
小波阈值降噪利用语义信息与随机误差在各尺度上的小波分解系数差异较大的特性,对小波系数进行阈值量化处理,以保证信号中的语义信息得到较好保存。 其中低频系数往往幅值较大,数目较少,包含较多语义信息,而高频系数则幅值较小,数目较多,往往包含大量随机误差。 小波阈值降噪主要分为如下三个步骤[30]:
①根据IMU 数据特点选择合适的小波基以及分解层数,对随机误差较大的IMF 进行小波分解。
②选择合适的阈值以及阈值函数,对各尺度的高频系数进行阈值量化处理,不改变低频系数,以去除各IMF 中的随机误差。
③对处理后的高频小波系数和低频小波系数进行小波逆变换,得到小波处理后的信号。
通过小波阈值降噪,可以对含有较大随机误差的高频IMF 分量进行精细化处理,在减小随机误差的同时,避免了IMF 分量中语义信息的大量丢失。将经过小波处理后的高频IMF 分量与无需处理的低频IMF 分量合并,通过经验模态分解逆变换得到经过信号增强的IMU 数据。
综上所述,完整的三阶段信号增强策略计算流程如算法1 所示。

算法1 三阶段信号增强策略
2 低成本惯性传感器的手势识别模型
传统的手势识别模型主要是基于时域频域对IMU 数据提取特征,然而由于低成本IMU 数据具有非线性强、随机误差大的特点,因此在时域、频域上对特征进行提取时,极易受到异常值、随机误差的影响。 而与时频域特征相比,复杂网络的统计指标基于网络的拓扑结构特征,受上述因素影响较小,同时能够从新的视角反映复杂系统所隐藏的内在规律。因此,本文将信号增强后的多元时间序列转换为复杂网络,以提取IMU 数据中内在的结构信息,并将复杂网络结构特征与时频特征相结合,利用随机森林模型进行分类,以实现低成本惯性传感器的高精度手势识别。 本文设计了多组实验以验证三阶段信号增强策略的有效性和复杂网络拓扑学特征在处理IMU 数据的优势。 具体实施流程如图3 所示。

图3 低成本惯性传感器手势识别模型流程图
2.1 多元时间序列转换为复杂网络
基于回归图方法将多元时间序列转换为复杂网络,我们需要对时间序列进行相空间重构。 根据Fraser 和Swinney[31]提出的互信息法,并结合杨志安等[32]提出的等间距格子法,可以确定时间延迟τ,使用伪近邻点改进方法[33]确定嵌入维数d。 然后,根据时间延迟和嵌入维数完成对原始时间序列的相空间重构。
在进行完整的相空间重构之后,本文可以将一维时间序列x(t)(t=1,2,…,N)表示为如下向量:
对于一个给定的阈值ε,本文可以得到任意两个空间向量之间的回归矩阵R(i,j):
式中:Θ为Heaviside 函数。
通过上式,可以得到一维时间序列对应的回归矩阵,以实现时间序列-复杂网络的转换。
进一步,为了更好地研究六轴惯性传感器数据之间的关系,本文将该方法扩展到多维,将多维时间序列XA,XB…XF转换为一个复杂网络。
对于来自同一个时间序列(以XA为例)的向量,本文定义(i,j)作为自回归矩阵:
而对于来自不同时间序列(以XA,XB为例)的向量,本文定义(i,j)作为交叉回归矩阵:
合并自回归矩阵和交叉回归矩阵,得到如下的多元时间序列的回归矩阵:
与此同时,为了保证同一个时间序列之间的两个向量相关性更强,本文需要保证同一时间序列之间的自递归率αauto高于和其他时间序列之间的交叉递归率αcross即:
因此,根据文献[34]本文设置同一个时间序列的自递归率为0.03,不同时间序列之间的交叉递归率为0.02,并根据递归率计算各递归矩阵中的阈值ε,进而得到多元时间序列的递归矩阵RX,实现将多元时间序列-复杂网络的转换过程。
2.2 复杂网络拓扑学特征
本文提取反映运动过程动力学性质的节点度、全局效率、平均路径长度等42 个复杂网络拓扑学特征,以实现高精度手势识别。 由于惯性传感器数据为多元时间序列,且各轴时间序列转换得到的多个复杂网络子图之间,具有较强的拓扑学关系,因此为更好地提取各个时间序列本身,以及多元时间序列之间的拓扑学特征,本文使用聚类系数的推广——交叉聚类系数与自聚类系数,以对复杂网络中各个子图进行更详细的分析。
局部交叉聚类系数是局部聚类系数在多元时间序列构成的复杂网络上的推广,其主要用于提取不同子图之间的聚类关系,其定义为:对于子图A上的节点i,它与另一个时间序列构成的子图B之间的局部交叉聚类系数(i)为:
而局部自聚类系数的定义则与原始聚类系数的定义类似,主要用于提取各个子图自身的聚类特征,故局部自聚类系数的定义[38]为:对于子图A上的节点i,它与自身时间序列构成的子图A之间的局部自聚类系数(i)为:
3 实验
3.1 数据采集和传感器型号
为保证数据集的多样性,以增强模型的泛化能力,我们邀请志愿者使用15 款不同型号的手机,进行26 个英文字母大小写以及0~9 十个数字共计62个手势动作的采集。 其中,惯性传感器为华为、小米等手机中内置的加速度计和陀螺仪,如ICM20690,LSM6DSM,LSM6DSO,其单价分别为0.28 元、0.40元、0.40 元。 本实验中所用到的惯性传感器的价格均未超过0.5 元。
志愿者使用不同型号的手机,每次对62 个手势动作进行连续采集,共计采集了150 次,然后本文通过先前提出的智能运动分割算法[39-40],将连续采集的惯性传感器数据,分割为代表各个单独手势动作的数据,即将采集的150 次数据分割为9 300 组数据,其中每组数据均由3 轴加速度数据、3 轴角速度数据构成,它们记录了1 个语义字符在空中书写的过程。 此外,我们用Nokov 光学运动捕捉系统与惯性传感器同步采集运动数据,进而为后续机器模型的训练、测试提供所需标签,实验场景如图4 所示。最终,本文将9 300 组数据随机划分8 500 组数据作为训练集,800 组数据作为测试集。

图4 借助光学传感器对惯性传感器进行标注
3.2 “EMD-CN-WT”三阶段信号增强策略
以手写动作‘A’的x轴方向加速度为例,对其进行经验模态分解,如图5 所示,原始时间序列被分解为从高频到低频的5 组IMF 分量。

图5 惯性传感器加速度信号x 轴分量的经验模态分解
为了更好地衡量各IMF 中随机误差的多少,本文通过将原始时间序列转换为复杂网络,以求得各IMF 分量确定性大小。 首先,本文要对各IMF 分量进行相空间重构。 为了提高计算效率,本文使用等间距格子法对互信息进行求解以计算时间延迟τ。如图6 所示,为了更细致地观察互信息与时间延迟的关系,本文将τ=30 处的局部放大,并选择互信息的第一个极小值点作为时间延迟τ,将其应用于相空间重构当中。

图6 互信息法确定时间延迟
然后,本文使用伪近邻点的改进方法,确定相空间的嵌入维数。 如图7 所示,在相空间嵌入维数为5 的时候,用于衡量伪近邻点数量的指标达到0.991,且随着维度的增加该值不再增大,即相空间已完全展开,因此本文选择将相空间展开为5 维。

图7 CAO 方法确定嵌入维数
在得到相空间重构后,本文通过式(2)计算各IMF 分量对应的邻接矩阵,将时间序列转换为递归图形式的复杂网络。 如图8(a)~图8(e)所示,可以发现随着IMF 分量频率逐渐降低,递归点分布的规律性逐渐增强,且递归点构成的线段逐渐与对角线平行。根据复杂网络“确定性”指标的定义规则可知,IMF 的确定性逐渐增强,随机性逐渐减弱。 在图8(f)中可以发现,前两个IMF 分量的确定性较弱随机性较强,随机误差较大,后三个IMF 分量的确定性较强随机性较弱,随机误差较小。 因此,选择随机误差较大的前两个IMF 分量,进行小波阈值降噪。

图8 第1~5 个IMF 分量的递归图(a)~(e)及其转换到复杂网络的确定性指标变化趋势(f)
由于手势运动数据本身的非平稳性较强,因此本文选择具有正交性和时频紧支撑性的Daubechies 4(db4)小波作为小波基函数,同时为避免阈值函数截断数据造成大量语义信息的损失,本文选取软阈值作为阈值函数并根据heursure 原则[35]选择启发式阈值,对随机误差较大的IMF 分量进行小波阈值降噪处理。 如图9 所示,本文专门对比了低成本IMU 和工业级高成本IMU 在信号增强前后轨迹还原的效果,以及不同成本惯性传感器的IMF 分量在小波处理前后的变化。 可以明显地发现,经小波处理后的IMF 确定性提高,随机性减弱,随机误差得到抑制,同时,低成本IMU 在经过信号增强后其轨迹还原效果与高成本IMU 轨迹还原效果相近,进一步体现了三阶段信号增强策略在处理低成本IMU信号时具有较大优势。

图9 不同成本IMU 在信号增强前后轨迹还原效果对比
3.3 结合复杂网络与时频特征的手势识别模型
在对62 个手势动作的低成本IMU 数据进行三阶段信号增强后,将复杂网络拓扑特征与时频特征相结合。 首先,本文将六轴传感器数据转换为复杂网络。 然后,提取2.2 节中复杂网络的聚类系数、平均路径长度、节点度等共计42 个拓扑特征,并提取六轴IMU 数据的方差、极差等时频特征。 将这两类特征相结合,并构建随机森林进行分类。 最终,在不同用户运动习惯各异、IMU 型号多样的条件下,结合复杂网络与时频特征的手势识别模型对62 种三维手势动作的识别精度达到了92.41%。
在低成本IMU 手势识别任务中,由于不同用户的运动习惯差异较大,部分字符本身具有多种书写方式,以及部分用户书写不规范,导致在进行实际动作采集时,相同语义字符往往具有多种运动形式,如图10 所示“5”“9”“j”三个字符具有多种书写方式。而对于同一个字符而言,不同书写方式所产生的IMU 信号,在时域、频域中存在较大差异。 因此,传统的手势识别模型容易将其识别为两个不同的动作,进而无法实现高精度的手势识别。 针对这一问题,本文对比了“5”“9”“j”三个字符在仅使用时频特征和将其与复杂网络拓扑学特征结合之后的手势识别精度,如表1 所示,可以发现,复杂网络因其可以提取数据间的结构信息和运动本身的动力学性质,使得手势识别模型可以较好地识别多种习惯的手势动作,增强了模型的泛化能力。

表1 具有多种书写习惯动作的识别精度
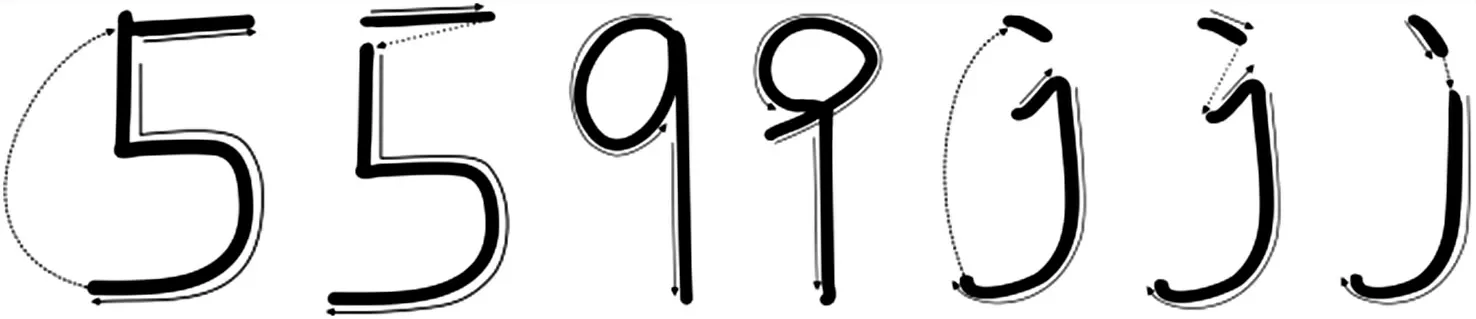
图10 具有多种书写习惯的手势动作
为了进一步呈现复杂网络拓扑学特征在手势识别任务与特征工程中的价值,本文分别使用原始的低成本IMU 数据和经过三阶段信号增强策略处理后的数据,通过不同的特征提取方法,设计了8 种消融实验。
实验1:直接将原始六轴IMU 信号输入BP 神经网络中进行分类。
实验2:直接将原始六轴IMU 信号输入长短期记忆网络(LSTM)中进行分类。
实验3:直接将原始六轴IMU 信号输入一维卷积神经网络(1D-CNN)中进行分类。
实验4:直接将原始六轴IMU 信号输入DSCNN[36]模型中进行分类。
实验5: 直接将原始六轴IMU 信号输入ResBlock-BiLSTM[37]模型中进行分类。
实验6:将时间序列转换为复杂网络,仅提取复杂网络拓扑学的42 个特征,并构建随机森林进行分类。
实验7:提取时间序列的方差、极差等时频特征,在不使用任何复杂网络特征的情况下,构建随机森林进行分类。
实验8:将时间序列转换为复杂网络,提取复杂网络42 个拓扑学特征,并与IMU 数据的时频特征相结合,共同构建随机森林进行分类。
基于以上八种不同IMU 特征提取方法的手势识别精度如表2 所示。 可以发现,在八组实验中基于三阶段信号增强策略处理后的IMU 数据,其手势识别精度均高于原始数据。 并且,在时频特征的基础上引入复杂网络拓扑特征,可显著提升IMU 手势识别的精度。

表2 不同特征提取方法下手势识别精度对比
同时,本文选取了多个用于手势动作识别的深度学习模型与本文提出的方法进行对比,可以发现在选取特征合适、充分的情况下,本文提出的方法不仅具有更强的解释性,且该方法的手势识别精度(92.41%) 可以超过深度学习模型识别精度(91.42%)。 该结果进一步体现了,在运动状态识别、时间序列分析领域内,复杂网络拓扑特征在特征工程中的重要价值,为模式识别提供了新的参考。
4 结束语
针对低成本惯性传感器数据包含有大量随机误差这一问题,本文提出了一种“经验模态分解-复杂网络-小波阈值降噪”三阶段信号增强策略,该策略利用复杂网络的“确定性”指标对经验模态分解得到的各IMF 分量的随机性进行评估,进而根据随机性的大小利用小波变换对各IMF 分量中的随机误差进行控制,实现了低成本IMU 的信号增强。 此外,基于复杂网络拓扑学特征不易受时频域上随机误差干扰的特点,本文在IMU 运动识别任务中将时间序列的时频特征与反映运动过程动力学性质的复杂网络结构特征相结合,并在不同用户运动习惯各异、IMU 型号多样且成本低廉的条件下,实现了62种三维手势动作的高精度识别。 最后,本文对比了机器学习与深度学习模型在低成本IMU 手势识别任务上的分类精度,可以发现在选取特征合适、充分的情况下,机器学习不仅具有更强的解释性,且机器学习的手势识别精度可以超过深度学习模型。
三阶段信号增强策略中,不同的小波基函数会导致信号增强效果具有较大的不同,因此未来工作将考虑构建深度学习模型对小波基函数进行自适应选取,并评估不同小波基函数对低成本IMU 数据的信号增强效果,以进一步提高低成本IMU 的手势识别准确度。
值得注意的是,由于低成本惯性传感器广泛地应用于智能手机、智能手表、游戏手柄等生活领域,因此本文提出的三阶段信号增强策略和手势识别模型具有广阔的应用场景和现实价值。
