双馈感应电机无速度传感器直接转矩控制方法*

蓝良生，陆正杰

(河池学院人工智能与制造学院，广西 宜州 546300)

在风电机组中，发电机的速度对风机的速度有很大影响，因此对风机的风能利用率也有很大影响。在风速较低时获得最大风能捕获量，风速较高时进行恒定功率控制，对发电机转速控制就显得尤为重要。 直接转矩控制是一种新兴的交流传动调速控制方法，该方法不需要改变磁场方向和坐标，而是直接控制磁通量和磁力矩，在一定程度上降低了电机结构的复杂度，使速度控制更加便捷、快速，变速风力发电机组的动态响应更加灵敏。 为了提高直接转矩控制方法的各方面性能，一般会将速度传感器应用在速度控制外环中，但在实际操作中，速度传感器不仅会增加整个机组的成本费用，还会约束伺服驱动装置的应用性能。 因此，无速度传感器越来越受到相关研究人员的重视，在国内外研究中也取得了一定的成效。

胡朝燕等[1]提出了开绕组永磁同步电机直接转矩控制研究。 设计了不同扇区划分方法及对应空间电压矢量组合的方案，降低了输出转矩脉动。 但是该方法仅考虑了单一运行状态下的电机转速控制情况，对于亚同步状态和超同步状态的电机转速控制效果有待进一步分析。 金国义等[2]提出了交流电机直接转矩控制扩速技术研究。 针对调速范围较窄的问题，建立了转矩模型和磁链模型，实现了交流电机直接转矩控制。 但是该方法对于亚同步状态和超同步状态的电机转速控制效果有待进一步分析。Ouyang 等[3]在考虑双馈发电机安全极限、风力发电预测误差、发电机旋转备用和系统运行成本影响的情况下，提出了一种新的动态减载思路。 建立了双馈发电机和蒸汽发生器的频率调节备用容量的分配原则，设计了基于双馈发电机最优减载参与频率调节控制的高比例风电电力系统分区调度模式。 但是该方法重点在频率调节控制，对于转速方面的控制效果有待进一步优化。

本文提出了双馈感应电机无速度传感器直接转矩控制方法。 在得到电机转速观测值的基础上，建立转子磁链模型；构建直接传感器的转矩控制系统，将其应用在双馈感应电机中，实现双馈感应电机转速的有效控制。

1 双馈感应电机转速观测

双馈感应电机的主要由定子、转子绕组两部分构成，作用是将电能输送到电网中，在四象限变频器的作用下，控制转子绕组的输入电流频率、幅值等信息，实现对变速风力发电机组的转速控制。 双馈感应电机在不同的发电状态下，对应不同的坐标系，具体如图1 所示。

图1 发电状态不同时，双馈感应电机对应参考坐标系

图1 中，ds-qs、dr-qr、de-qe分别为两相静止参考坐标系、转子绕组旋转坐标系、同步旋转坐标系。de-qe位于转子的磁链ψr上，与dr-qr之间存在转差角度θsl。 与此同时，ψr也对无速度传感器的转速进行控制。

由图1 可知，θr＝θe＋θsl，那么转子的转速ωr为:

由式(1)可知，想要得到双馈感应电机转速ωr，前提是先得到转子磁链同步转速ωe和转差速度ωsl的值，接下来对二者的值进行计算。

1.1 转子磁链同步转速ωe 的估算

根据图1，计算同步旋转磁链角θe:

式中:ψsrq、ψsrd分别表示ψr在ds-qs和de-qe坐标系下的轴分量。

在ds-qs坐标中，转子磁链ψr方程由式(3)表示，控制磁链方程由式(4)表示:

式中:Lr表示转子绕组在电机作用下产生的电感，Lc表示控制绕组在电机作用下产生的电感，Mpr表示功率绕组与转子绕组在相互影响下，二者之间产生的互感，Mcr表示控制绕组与转子绕组在相互影响下，二者之间产生的互感，i表示静止坐标系下，功率绕组自身的矢量值。

通过计算式(3)和式(4)可以得到ψr的估算结果，从而得到同步转速ωe的估算值。

1.2 转差速度ωsl的估算

在同步旋转坐标系中，进一步推理得到转差速度[4]ωsl的值:

本文仅考虑两相静止坐标系下的双馈感应电机，所以，需在de-qe和ds-qs坐标系之间完成转换。通过参考图1，构建二者之间的变换矩阵[5]方程:

通过计算转差速度，即可得到转差速度ωsl的估算值。

2 实现直接转矩控制

在选择转子电压空间矢量基础上，根据第1 节内容观测和计算得到双馈感应电机转差速度ωsl，基于该结果计算磁链模型及电磁转矩、转子磁链与电流夹角，并通过添加离散两点式调节器实现直接转矩控制。

2.1 转子电压空间矢量选择

建立一个图2(a)所示的a-b-c坐标系，在a、b、c三个方向上，转子磁链[7]产生的投影分别用ηa、ηb、ηc来表示。 转子磁链6 个区段(S1～S6)的分割原则为:当正好存在某个轴上的磁链投影分量过零时，该点即为区段的分界点。 图2(b)所示为亚同步状态下，电压开关信号的生成规则。Sηa、Sηb、Sηc表示不同方向上磁链开关信号，SUa、SUb、SUc表示不同方向上转子电压开关信号，U2＋、U2-分别为在转子电流与磁链夹角增加和减小的情况下所产生的电压矢量[8]。

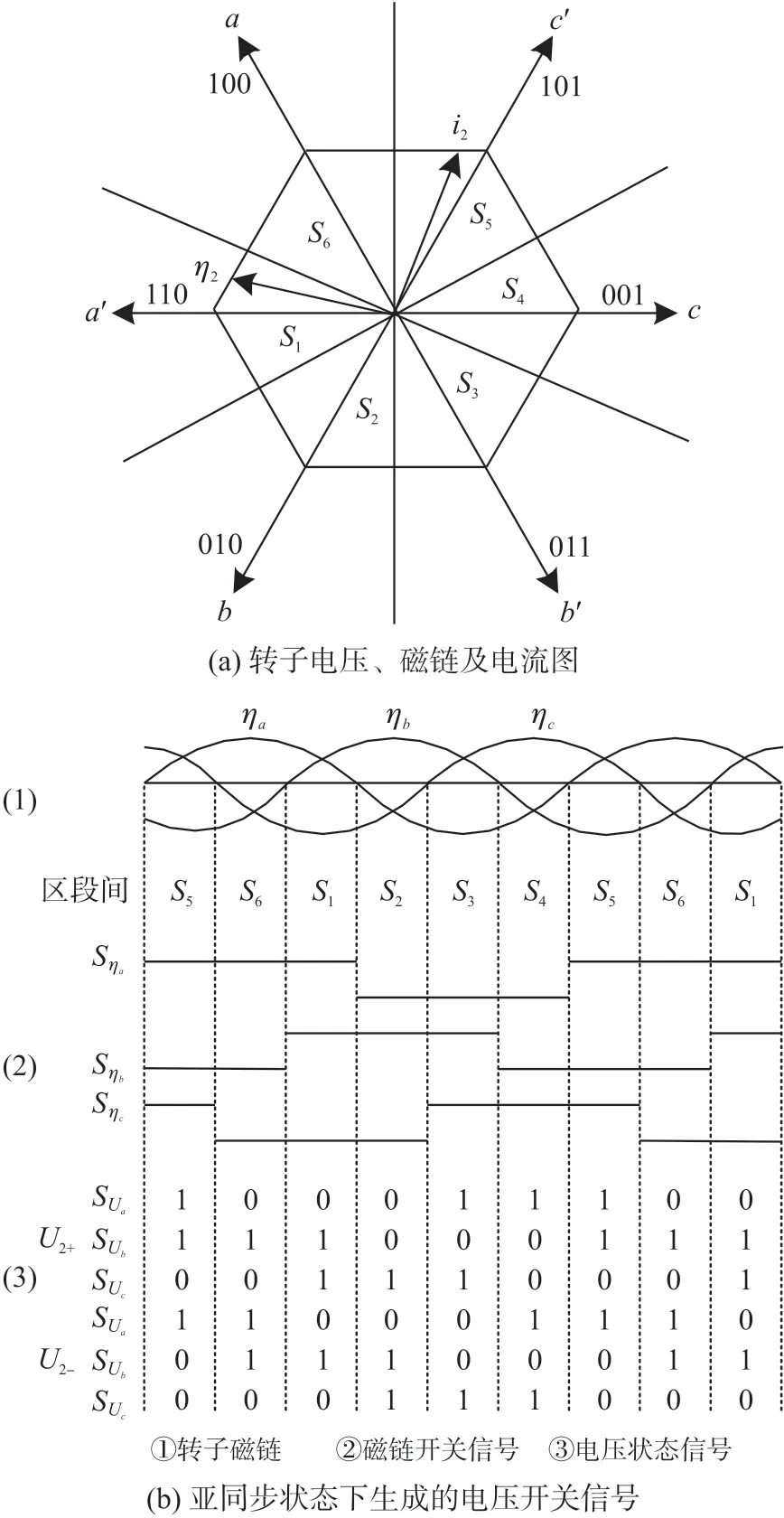
图2 转子绕组电压空间矢量分析

在图2(b)中，比较(2)、(3)，可以得到亚同步状态下的Sηa、Sηb、Sηc与SUa、SUb、SUc之间的关系:

U2＋与磁链开关状态之间的逻辑关系定义公式为:

U2-与磁链开关状态之间的逻辑关系定义公式为:

按照上述思路，计算同步工况下Sηa、Sηb、Sηc与SUa、SUb、SUc之间的关系:

U2＋与磁链开关状态之间的逻辑关系定义公式为:

U2-与磁链开关状态之间的逻辑关系定义公式为:

通过式(7)～式(10)，可以通过逻辑法实现开关信号的产生。

2.2 磁链模型及电磁转矩计算

双馈感应电机的两大组成部分为定子绕组和转子绕组，二者分别产生磁势矢量和转子磁势矢量[9]。 通过将两个矢量做相乘计算，得到电机的电磁转矩[10]。

双馈感应电机的定子、转子绕组电压计算公式为:

式中:x表示电机绕组等式，y表示电机绕组变量，u、h分别表示电机中的电压、电流，φx、φy分别表示电机中的定子、转子磁链。

双馈感应电机的电磁矩阵[11]计算公式为:

式中:γ表示在磁链空间内，定子绕组和转子绕经过调整后形成的夹角，K表示电磁矩阵系数。

与其他感应电机有所不同的是，双馈感应电机可以对转子电流直接进行测量，因此，利用电流模型[12]可求出磁链的空间矢量，同时还可有效降低电压模型产生的积分累计误差。 计算公式为:

根据克拉克3/2 原理，计算极坐标系下电流空间矢量表达式，如式(14)所示:

式中:θs表示极坐标下的转子电流[13-14]，α(m1，n1)、β(m2，n2)是存在于复平面中的两个矢量。

2.3 直接转矩控制方法

直接转矩控制方法的速度由转矩和转速两部分来实现，在转速部分，本文添加了线性调节器[15]；在转矩部分，本文采用离散两点式调节器，启动方式为串电阻启动。 当发电机组的转速达到预先设定的值后，自动转矩控制系统自动接入到电机中。

在亚同步状态下，如果电机转速相对给定值小很多，速度调节器的输出将会呈现上升趋势，直到达到给定值要求。 在实际转矩值没有达到理想值时，调节器不做任何功，输出为0，与之相对应的逆变器输出就是零电压，由此增加了电机的扭矩，进而带动电机速度提高。 相反，如果调节器的输出是1，逆变器输出就变成非零电压，θs的值就会变得很小，从而电磁扭矩也会相应地降低，从而使电机速度减慢。

3 仿真测试与结果分析

为了验证本文方法在实际应用中是否具有一定的有效性和合理性，在MATLAB 平台中，利用本文方法控制双馈感应电机直接转矩，并从转速阶跃响应曲线、输出转子绕组和定子绕组的电流和电压波形变化、无功调节响应曲线以及稳态状态下的转子磁链运行轨迹几个方面进行测试，具体测试结果如下。

3.1 双馈感应电机参数设置

图3 所示为本文测试的双馈感应电机直接转矩控制系统仿真结构。

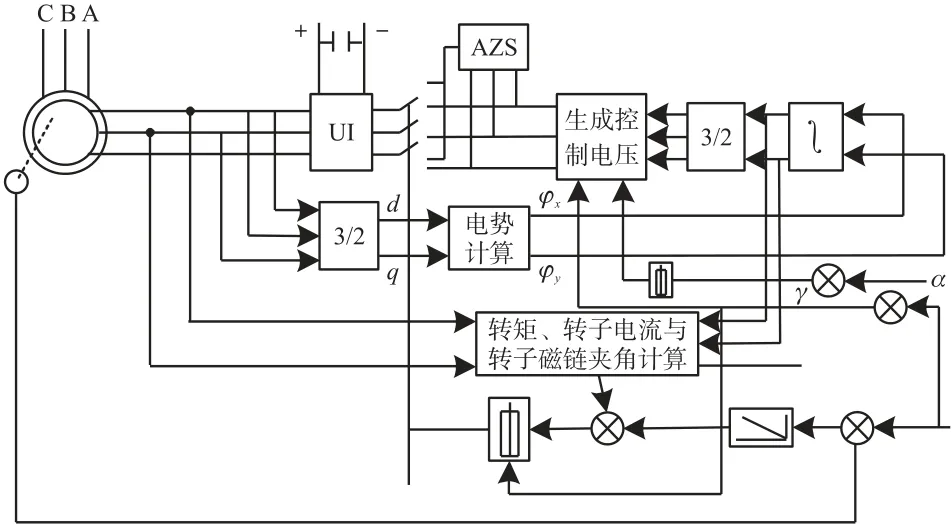
图3 直接转矩控制系统

直接转矩控制系统中的各项参数:电机功率为2.2 kW，定子绕组电压为380 V，定子、转子绕组电感Ls＝71.3 mH、Lr＝71.3 mH，Rr＝0.816 Ω，Lm＝69.31 mH。

3.2 仿真结果及分析

图4 所示为本文方法应用后的双馈感应电机转速阶跃响应曲线。

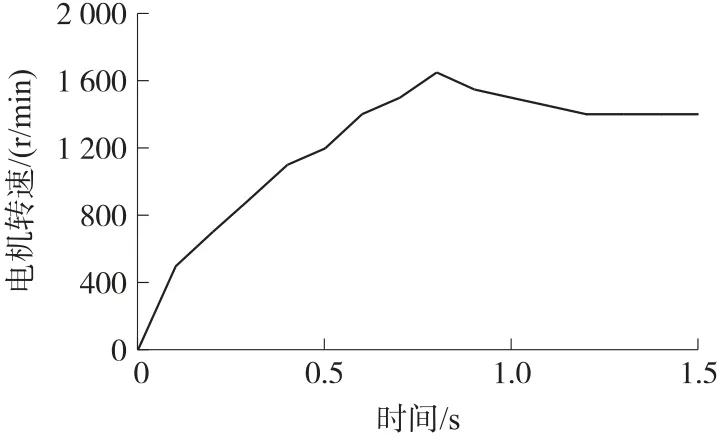
图4 电机转速阶跃响应曲线

从图4 中可以看出，0 s～0.4 s 为感应电机串电阻启动阶段，电机瞬间加速至1 100 r/min，0.4 s 之后接入直接转矩控制系统，电机转速持续增加并稳定在给定转速1 200 r/min 处，在0.6 s 时转速为1 400 r/min，在0.8 s 时转速为1 650 r/min，1.2 s 之后转速始终保持为1 400 r/min。

为了进一步验证所提方法的控制效果，在亚同步和超同步状态下测试本文方法的控制效果，输出转子绕组中电流波形变化情况，如图5(a) 和图5(b)所示。

图5 不同状态下的转子绕组电流变化波形情况

由图4 的转速阶跃响应曲线可知，电机在0.4 s后接入直接转矩控制系统，后续转速虽有一定波动，但相对稳定。 结合图5 的转子绕组变化波形情况可知，在0.4 s 前无论是亚同步状态还是超同步状态，其转子电流波动幅度较大，在-70 A ～75 A 左右。在0.4 s 后，本文方法控制后的转子绕组电流变化波形变化幅度较小，且相对稳定，与电机转速阶跃响应曲线分析结论基本一致。 因此，本文方法能很好地完成超同步与亚同步之间的控制，并保持良好的转矩控制能力，对双馈感应电机的转速也有了更高效的控制和跟踪。

由图5 可知，电机在0.5 s～1.0 s 趋于稳定。 为此，选用文献[1]开绕组永磁同步电机直接转矩控制方法、文献[3]基于双馈发电机动态减载控制方法作为所提方法的对比方法。 分析0.5s～1s 时电机的控制效果，即电机是否趋于稳定，得到三种方法的定子绕组的电流波形变化情况，如图6 所示。

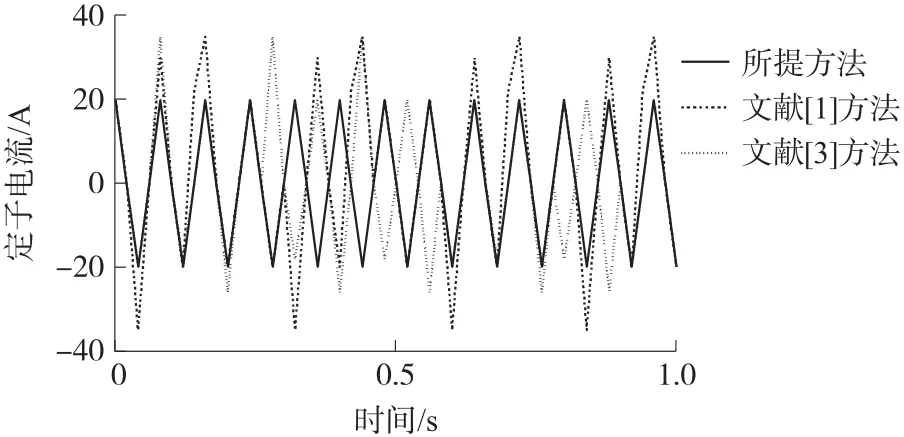
图6 0.5 s～1.0 s 区间内定子电流波形

分析图6 可知，运用本文直接转矩控制方法后，定子绕组电流均表现为正弦状态，将对风力发电的污染控制在最低，且电流波形在-20 A ～20 A 之间波动，未出现极大值或极小值。 而两种对比方法虽然定子绕组电流也表现为正弦状态，但是在控制过程中出现了极大值或极小值。 综上分析可知，本文直接转矩控制方法稳态性能较好。

图7 所示为无功功率在转速为1 200 r/min 时的曲线变化情况。

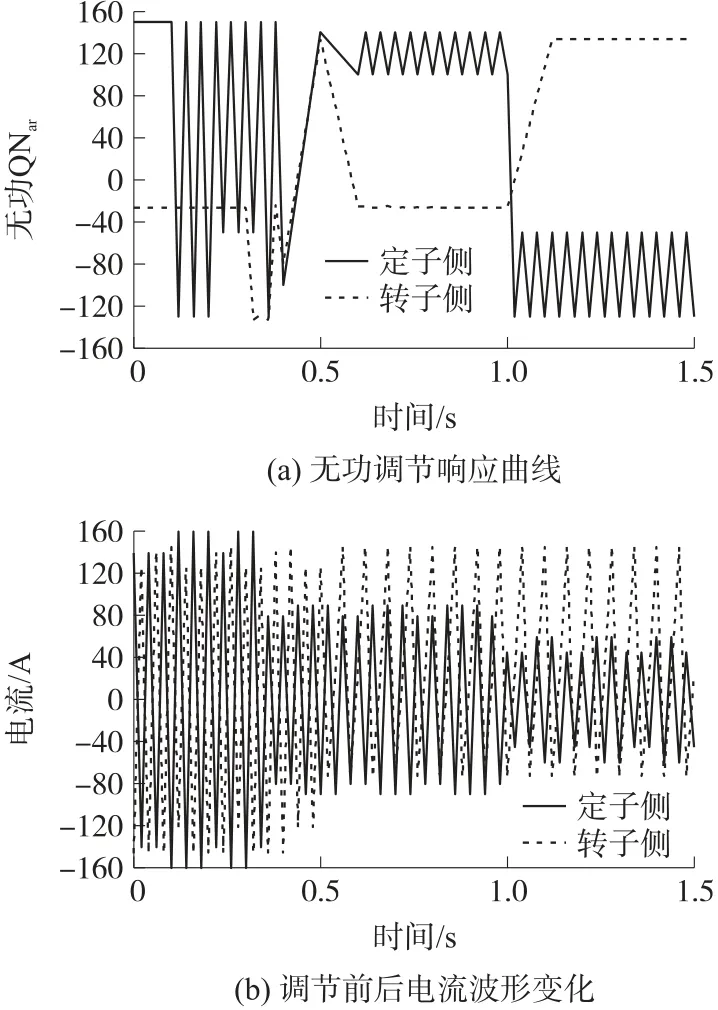
图7 1 200 r/min 下无功调节响应曲线

观察图7 可知，在0.5 s 后，电机转速逐渐转换为稳定运行状态，在1.0 s 后进入无功调节状态。 对比调节前后，定子和转子电流始终保持为正弦波形，同时转子的电流有了明显的增大趋势，这是因为励磁分量增大造成的；与转子电流相反的是，定子电流呈下降的趋势。 这是由于转子在定子电流中产生了一个很小的励磁分量，而定子电流没有磁场保护，因此出现了下降趋势。 不仅如此，从该图中还可得知，只要对电动机转子无功进行一定的调整，就可以使无功功率发生较大改变。

图8 为稳态状态下的转子磁链运行轨迹。

图8 稳态运行状态下电机转子磁链轨迹

从轨迹的运行情况中可以看出，本文提出的直接转矩控制方法可以保证转子磁链的运行轨迹基本保持为圆形。

4 结论

本文针对双馈感应电机无速度传感器，提出了一种直接转矩控制方法。 通过对双馈感应电机转子磁链同步转速和转差速度进行计算后，对转子绕组的电压空间矢量展开分析，建立磁链模型，实现对电磁转矩的计算；最后利用调节器，改变转子电流空间矢量值，实现对双馈感应电机的转速控制。 在仿真测试中，本文方法展现出了较好的阶跃响应效果，并对电机转子和定子的无功功率实现了较好控制，使稳态状态下的定子、转子电流展现为正弦波形，保证对风力发电的污染程度为最低。