城市轨道交通车辆用不锈钢蜂窝应变率敏感性研究*

陈佳明 朱 涛 肖守讷 丁浩谞 阳光武 杨 冰

(西南交通大学牵引动力国家重点实验室, 610031, 成都∥第一作者, 硕士研究生)

蜂窝是一种二维多孔材料,具有密度小、成本低、变形模式可控等特点,其作为一种优良的吸能材料,被广泛应用于汽车、轨道交通和航空航天等领域。在城市轨道交通领域,蜂窝结构被大量运用在车辆防爬器的吸能区和司机室的端部结构,以在车辆发生碰撞事故时吸收巨大的碰撞能量。

目前,国内外的学者已对蜂窝结构的静态变形模式、动态变形模式及其力学性能做了大量研究。文献[1]通过对正六边形蜂窝结构进行共面动态压缩数值模拟,得出了基材的应变率强化效应会使蜂窝的动态峰值应力增加的结论。文献[2]在对组合式铝蜂窝的试验研究中发现,与准静态结果对比,动态加载条件下,组合式蜂窝结构的吸能效果更好。文献[3]研究了一种不锈钢蜂窝的静态和动态压缩特性,研究结果表明不锈钢蜂窝的压溃强度大大超过同等规格的铝合金蜂窝,在吸能方面有一定的优势。文献[4]研究了一种以应变率不敏感的铝合金作为基体材料的蜂窝,发现其动态强化效应与蜂窝本身的结构有关。在速度较大的冲击作用下,蜂窝的压溃载荷有明显的动态变化,尤其对于应变率敏感材料,这种变化很大程度上是由于材料的性能造成的。

与传统铝蜂窝相比,不锈钢蜂窝因具有更大的额定吸能容量,可以作为车辆端部吸能的材料,现已被中车长春轨道客车股份有限公司应用于防爬器的吸能区。目前,国内外关于考虑应变率效应对蜂窝结构变形、载荷和吸能方面影响的研究较少。基于此,为了研究不锈钢蜂窝应变率敏感性对其动态冲击性能的影响,本文建立了不锈钢蜂窝异面压缩数值模型,并与文献[3]中不锈钢蜂窝的准静态压缩试验和动态冲击试验进行对比分析。在此基础上,本文还模拟分析了不同应变率对不锈钢蜂窝结构材料冲击响应的影响。本文研究可为不锈钢蜂窝在城市轨道交通车辆上的设计研发提供参考。

1 不锈钢蜂窝结构有限元模型及验证

1.1 建立不锈钢蜂窝仿真模型

采用两种不同规格的不锈钢蜂窝进行仿真建模。蜂窝1的尺寸为160 mm×160 mm×120 mm,胞元边长l为2.5 mm,壁厚t为0.15 mm;蜂窝2的尺寸为160 mm×160 mm×80 mm,胞元边长l为2.5 mm,壁厚t为0.18 mm。规定平行于波纹板的方向为L方向,沿着蜂窝的叠加方向为W方向,蜂窝通过异面压缩,沿着其高度方向T有序变形,从而吸收能量。不锈钢蜂窝各方向定义示意图如图1所示。

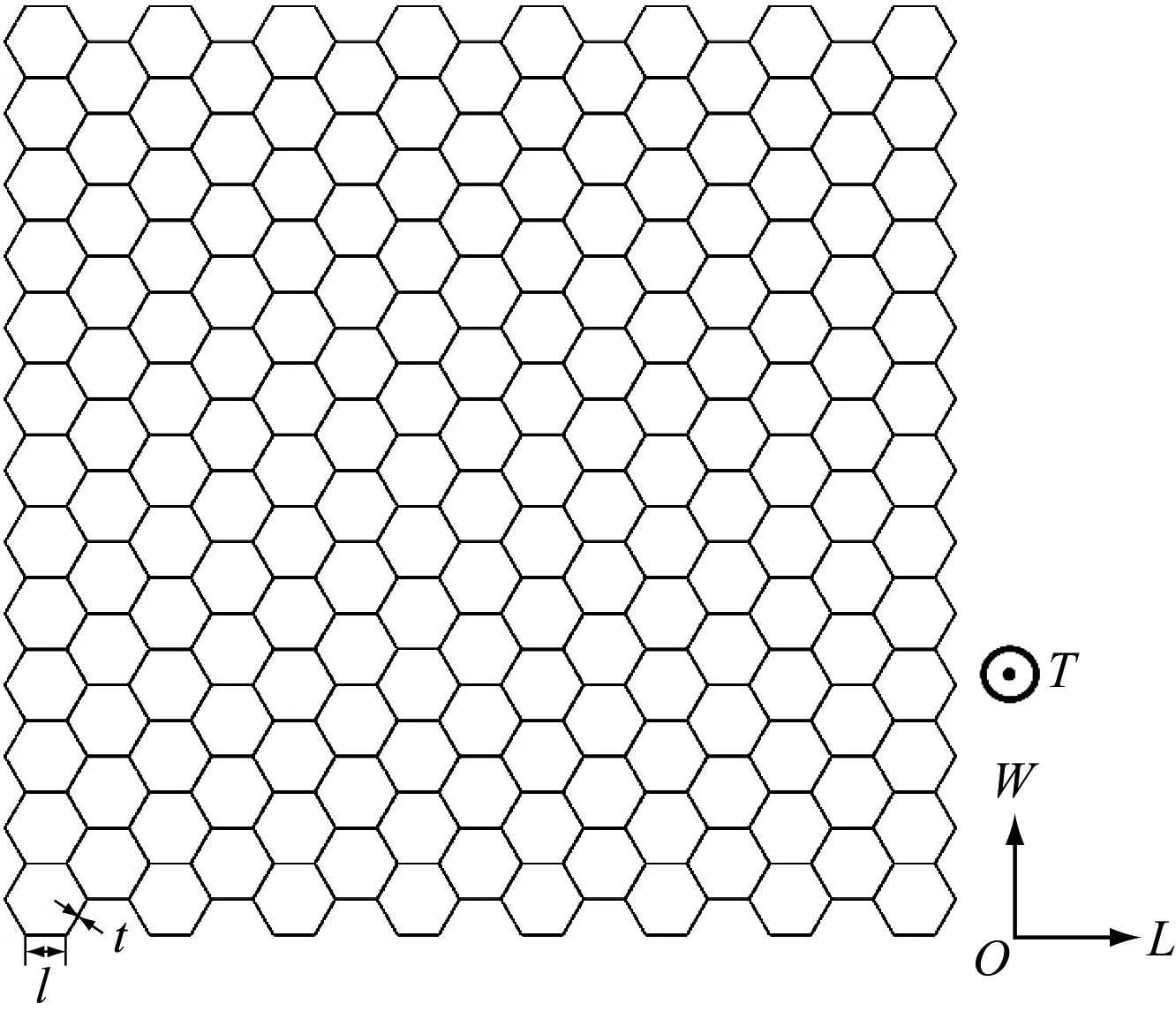
图1 不锈钢蜂窝各方向定义示意图

蜂窝所使用的不锈钢材料为304不锈钢,具有耐高温、耐腐蚀及热加工性好等优良特性,常用于耐酸、耐碱和耐腐蚀等关键零部件。在准静态压缩工况下,不考虑材料的应变率效应,仿真模型中只输入材料的基本参数。不锈钢蜂窝有限元模型如图2所示。不锈钢蜂窝下端与底板相连,刚性墙沿T方向匀速或以冲击速度压缩不锈钢蜂窝。建立刚性墙和蜂窝的面面接触和蜂窝的自接触,在底板处施加约束。为检验模型的可靠性,以上几何参数和材料参数与文献[3]中保持一致。

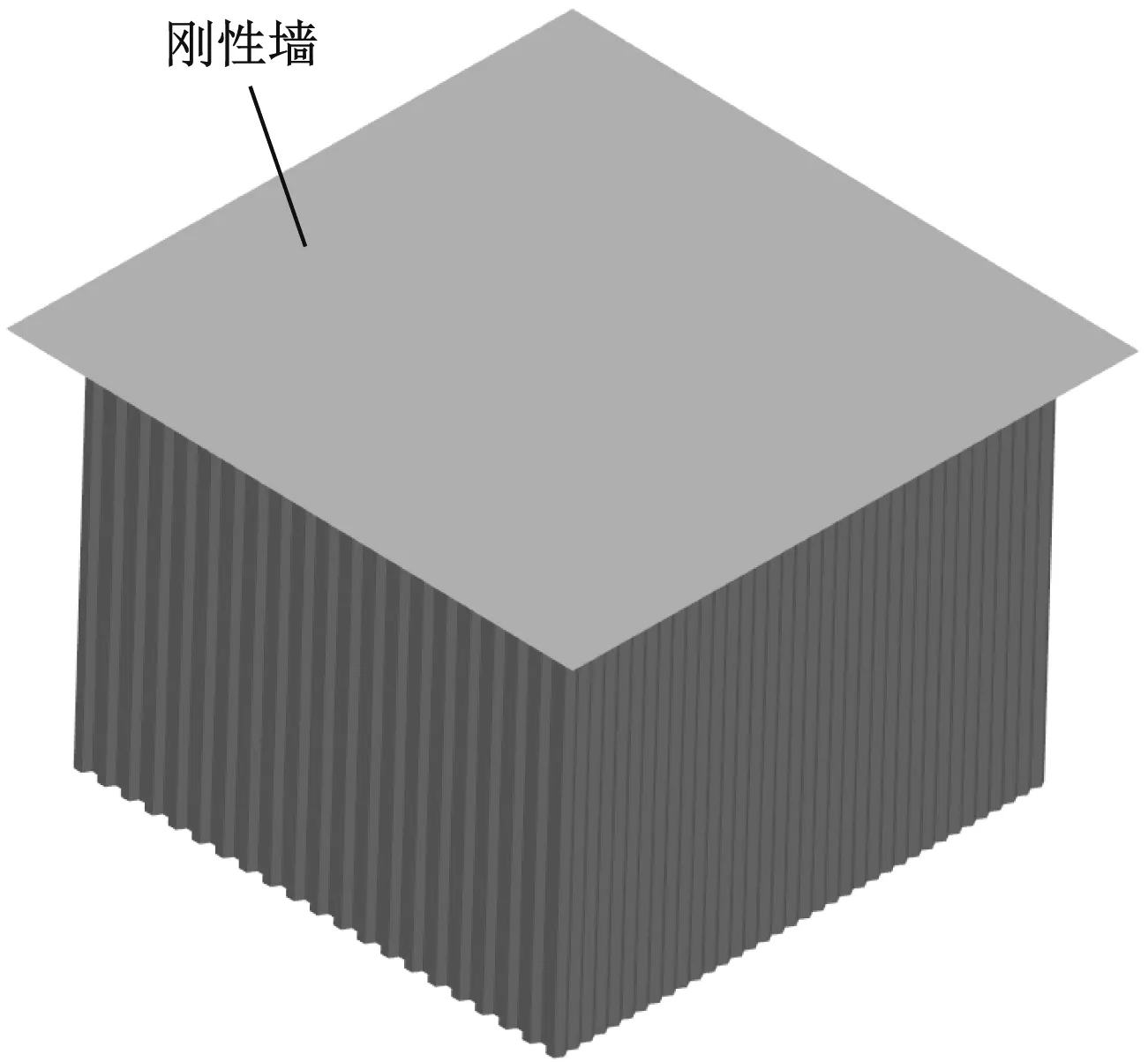
图2 不锈钢蜂窝有限元模型

1.2 验证不锈钢蜂窝仿真模型

蜂窝的压溃应力是由准静态压缩时的压溃力除以蜂窝在L-W截面上的截面面积所得到的,该截面上的面积采用等效面积法计算。将每3个相邻蜂窝的中心相连,这样每3个蜂窝中间就有1个三角形,每个三角形中包含一个Y字型蜂窝,计算所有Y字型蜂窝的面积即为截面面积。经计算可知,该模型中共有1 440个Y型蜂窝,L-W上的截面面积为22 382 mm2。

蜂窝进入稳定压溃阶段平稳段的平均压溃应力是衡量蜂窝吸能特性的重要指标之一。文献[5]将明显进入稳定屈服阶段的所有数据采集点取平均值,以获得稳定压溃阶段平稳段的平均压溃应力。这种方法可以最大程度地减小由弹性变形曲线截断点的不确定性所带来的数据波动,本文也采用这种方法。

对仿真结果和文献[3]的试验结果进行对比,不锈钢蜂窝准静态压溃应力-位移曲线对比如图3所示。由图3可知,通过有限元计算得到的两种规格不锈钢蜂窝的平均压溃应力与文献[3]中的试验结果基本一致,其整体应力趋势也与文献[3]相符。经计算可知:蜂窝1的仿真平均压溃应力为34.92 MPa,与试验结果36.44 MPa之间的误差为4.17%;蜂窝2的仿真平均压溃应力为43.15 MPa,与试验结果45.30 MPa之间的误差为4.75%。两次仿真结果的误差不超过5%,在可以接受的范围内,从而验证了准静态压缩工况下所提有限元模型的准确性。

2 应变率效应对不锈钢蜂窝结构压溃应力和吸能的影响

由于两种规格蜂窝结构的准静态和动态拉伸试验结果类似,故接下去的仿真试验中仅取蜂窝1的规格参数进行分析。将试验所得的304不锈钢蜂窝在不同应变率下的应力-应变曲线输入材料模型,分别计算落锤的冲击速度为5.0 m/s、7.5 m/s和10.0 m/s情况下,不锈钢蜂窝在考虑应变率效应和不考虑应变率效应条件下的冲击压溃情况。考虑应变率效应的304不锈钢蜂窝准静态和动态拉伸试验结果如图4所示,将其作为材料参数输入有限元模型,不考虑应变率效应的有限元模型不作设置。

2.1 应变率效应对压溃力影响分析

3种冲击速度下的压溃应力-位移曲线如图5所示。由图5可以知道,考虑了应变率效应的不锈钢蜂窝峰值压溃力、平均压溃应力明显增大。这说明304不锈钢蜂窝具有应变率强化的力学响应特征。从材料流动应力角度来看,应变率强化效应使得不锈钢材料的流动应力变大,导致不锈钢蜂窝每个单元的平均应变率减小,相比于不考虑应变率效应的情况,所产生相同应变的时间会缩短,这增加了不锈钢蜂窝的抗冲击性能,因此平均压溃应力有所增加。

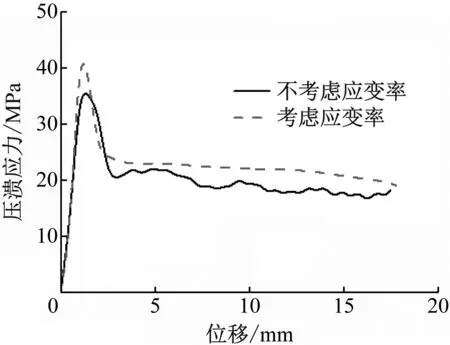
a) 冲击速度为5.0 m/s

对比考虑应变率效应和不考虑应变率效应两种情况,3种冲击速度下,不锈钢蜂窝的峰值压溃应力和平均压溃应力如表1所示。由表1可知:考虑应变率效应的不锈钢蜂窝平均压溃应力的增加量为7.9%～12.6%,而峰值压溃应力的增加量为13.3%～17.3%,峰值压溃应力受应变率的强化作用更明显;两者对于应变率的敏感性随着冲击速度的增加而有所降低。

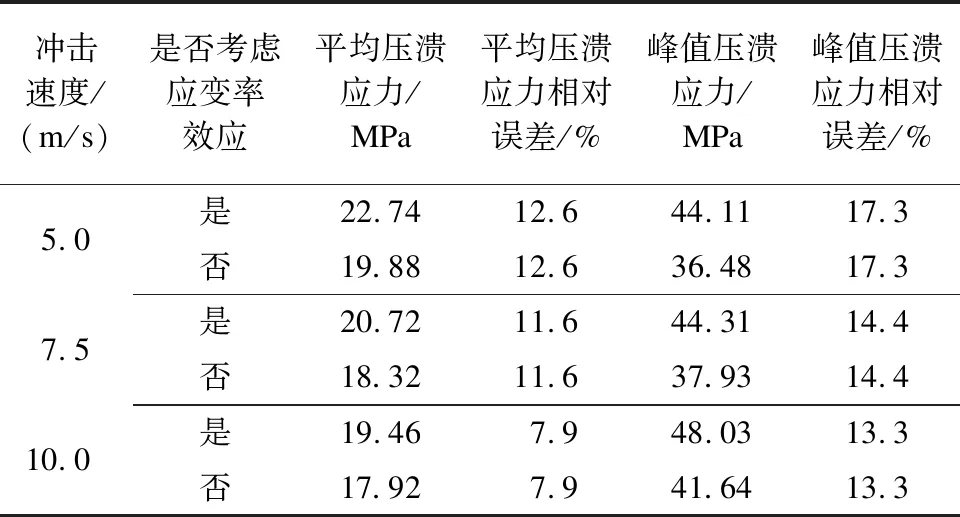
表1 3种冲击速度下不锈钢蜂窝的峰值压溃应力和平均压溃应力

在实际试验过程中,由于不锈钢蜂窝材料的应变率敏感性,在每一层蜂窝发生屈服的过程中,其流动应力会有所增大,这种放大效应削弱了由蜂窝单元折叠变形所造成的应力下降,因此试验中的压溃应力曲线是较为光滑的,振荡并不明显。由此可见,考虑材料应变率效应所得的仿真结果与试验结果的吻合度更高。

2.2 塑性变形吸能和理想吸能效率

文献[6]在低速冲击试验研究中发现,在吸能过程中,蜂窝结构的总吸能量主要转化为塑性变形能和应变能。比吸能是评估结构吸能特性的指标之一,包括质量比吸能和体积比吸能,但由于本文对比的是同种规格蜂窝的吸能特性,两者的质量和体积相同,因此引入理想吸能效率作为评估指标。理想吸能效率值越接近100%,表明结构的吸能效果越好。

对比考虑应变率效应和不考虑应变率效应两种情况,3种冲击速度下不锈钢蜂窝的塑性变形吸能、最大压缩位移和理想吸能效率如表2所示。由表2可以知道:是否考虑应变率效应对于不锈钢蜂窝的塑性变形吸能影响较小,误差在2%以内;不锈钢蜂窝的理想吸能效率随着冲击速度的增加而有所降低;考虑了应变率效应的不锈钢蜂窝的最大压缩位移和理想吸能效率均小于未考虑应变率效应的情况。

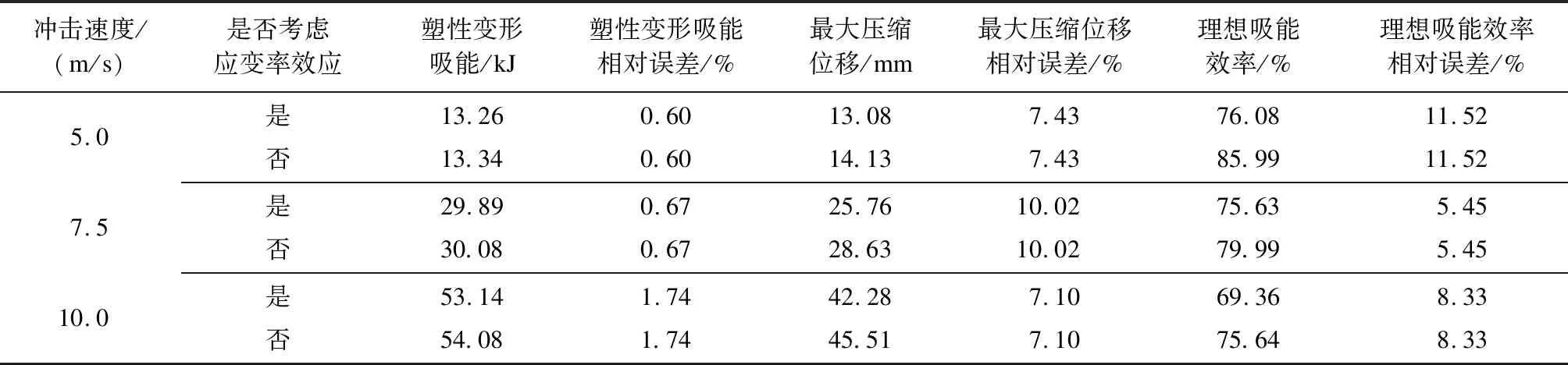
表2 3种冲击速度下不锈钢蜂窝的塑性变形吸能、最大压缩位移和理想吸能效率

综上所述,在对304不锈钢蜂窝进行实际设计时,若不考虑应变率效应的影响将会高估不锈钢蜂窝的吸能能力,且过大的峰值应力会产生过大的加速度,对于被动安全性防护是不利的。因此,在设计中对蜂窝的吸能量和峰值应力等技术指标应预留一定的安全裕量。

3 应变率效应对不锈钢蜂窝变形模式的影响

3.1 不锈钢蜂窝变形模式对比

不锈钢蜂窝的准静态压溃变形共经历4个阶段:①弹性阶段;②到达应力峰值后进入屈曲状态阶段;③稳定压溃折叠变形阶段;④压实阶段。不锈钢蜂窝动态冲击的压溃变形模式只有前3个阶段,将冲击能量吸收完后,应力逐渐降低为0。

3种冲击速度下,最上层不锈钢蜂窝的压溃初期应变云图如图6所示。在考虑了应变率效应后,由于第一层不锈钢蜂窝折叠变形形成塑性铰所需的应变增大,在相同压溃力的加载作用下,未考虑应变率效应的不锈钢蜂窝达到形成塑性铰的应变时,考虑应变率效应的不锈钢蜂窝还未形成塑性铰,此时应变进一步向后传递,表现为上层蜂窝的初始塑性应变单元数目增多。

图6 3种冲击速度下最上层不锈钢蜂窝的压溃初期应变云图

3种冲击速度下,不锈钢蜂窝吸能后的应变云图如图7所示。未考虑应变率效应时:不锈钢蜂窝的变形主要通过自上而下的结构渐进压缩折叠及逐层变形将外力做功吸收,直至吸收完落锤的全部冲击能量;与底板连接的不锈钢蜂窝几乎没有发生塑性变形。考虑应变率效应时:下层不锈钢蜂窝的应变较大,且随着冲击速度的增加,下层不锈钢蜂窝产生的塑性应变单元有所增多,塑性变形更为明显;在冲击过程中,不锈钢蜂窝的外壁出现了鼓胀变形,且随着冲击速度的增加,鼓胀变形更为明显;上层不锈钢蜂窝没有出现整层的稳定压溃现象,而是从四周向蜂窝中心产生了渐进压溃变形;冲击能量由上下层蜂窝共同吸收。

图7 3种冲击速度下不锈钢蜂窝吸能后的应变云图

3.2 不锈钢蜂窝变形模式机理分析

如果在蜂窝L-W截面中取出一个Y字型单元,蜂窝可以看作是有许多个该单元组成的多孔结构。每个Y字型单元可看作一个塑性杆。上述不锈钢蜂窝在不同应变率下变形模式的差异可以用塑性杆的压溃折叠理论来解释。

文献[7]通过数值计算发现,在弹塑性柱上方施加一压溃力,由于产生垂直于压溃力方向的横向加速度,柱的屈曲将发生在较大的应变处。若弹塑性柱具有应变硬化行为,屈曲峰值力也将增加。刚塑性杆的塑性失稳临界载荷为[7]:

(1)

式中:

b、d——杆截面的边长;

P——绕塑性铰转动的力臂;

θ——转动角度;

σS——杆的塑性流动应力。

由横向惯性理论,在理想状态下杆的压缩过程中,杆中心处有一集中质量点在横轴方向会有加速度。该加速度受到塑性流动应力的影响[7]:

(2)

式中:

m——杆的质量;

要想达到与冲击速度相协调的沿横轴的加速度是需要一定时间的。在这之前,刚塑性杆主要发生的是沿纵向的压缩变形,转动角度变化较小,集中质量点沿横轴的位移较小。若刚塑性杆材料是应变率强化材料,则刚塑性杆发生屈曲的所需应变更大。一旦越过屈曲所需的应变,转动角度迅速增大,加速度随之迅速增大,刚塑性杆发生折叠。因此在冲击载荷的作用下,考虑应变率效应的刚塑性杆到达压溃折叠前所需的纵向压缩应变更大,这也符合图7的应变云图。在冲击作用下,考虑应变率效应的不锈钢蜂窝上层蜂窝屈曲折叠所需的应变更大,不锈钢蜂窝沿压缩方向的应变也更大,轴向力会进一步向下层蜂窝传递。在轴向力的作用下,底层蜂窝逐渐达到了屈曲所需的应变,与上层蜂窝一起产生稳定逐层的压溃折叠。此外,初始缺陷也有着重要的影响,刚塑性杆的初始缺陷越小,在刚塑性杆材料具有应变率强化效应的情况下,屈曲所需的峰值力也就越大。由于在仿真中所建立的模型是理想状态的,并不像实际试样有初始缺陷,故这种应变率强化效应也就表现得更为突出。

4 结论

1) 304不锈钢材料具有明显的应变率强化效应。不考虑应变率效应的压溃应力-位移曲线有明显的上下振荡趋势,而考虑应变率后的压溃应力-位移曲线较为光滑,与试验结果更为接近。在对304不锈钢蜂窝进行实际设计时,其应变率效应对额定吸能容量是有利的,但需注意控制较大的峰值应力。

2) 在冲击载荷作用下,考虑应变率效应的不锈钢蜂窝平均压溃应力增加了10%左右,峰值压溃应力增加了15%左右,表现出更强的应变率敏感性。不锈钢蜂窝的塑性吸能总量变化不大,最大压缩位移和理想吸能效率均有所减少。

3) 应变率效应会使蜂窝结构形成塑性铰所需的应变增大。在冲击载荷作用下,考虑应变率效应的不锈钢蜂窝的上层蜂窝初始塑性应变单元数目有所增多。随着冲击速度的增加,下层蜂窝产生的塑性应变单元数量增多,塑性变形更为明显。考虑应变率效应的不锈钢蜂窝外壁出现了鼓胀变形,且随着冲击速度的增加,该鼓胀变形更为明显。在蜂窝基体材料为应变率敏感材料时,需注意此类变形模式造成的影响。