勾股定理在实际生活中的应用

曹洪

勾股定理及其逆定理是几何学中一颗光彩夺目的明珠，其应用十分广泛，被誉为“几何学的基石”. 现举例说明其在实际生活中的应用，供同学们参考学习.

一、是否合格

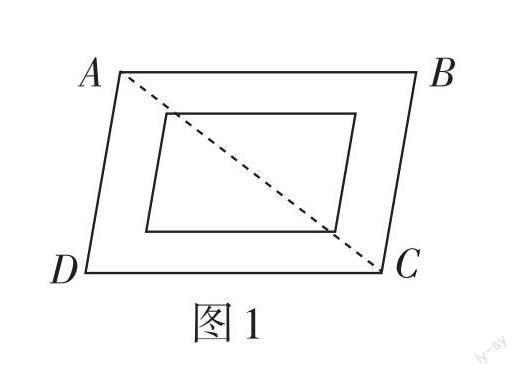
例1 图1是一农民建房时挖的地基平面图，按标准应为长方形，他挖完地基后测量了一下，发现AB = DC = 8 m，AD = BC = 6 m，AC = 9 m，请你帮他看一下他挖的地基是否合格.

解析：要判断地基是否合格，就要看他挖的四边形的四个角是否都是直角. 在   △ADC中，AD2 + DC2 = 62 + 82 = 100，AC2 = 92 = 81，∴AD2 + DC2 ≠ AC2，∴△ADC不是直角三角形，∴∠ADC不是直角. 因此，该农民挖的地基不合格.

二、飞行多远

例2 如图2，有两棵树，一棵高10米，另一棵高4米，两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢，这只小鸟至少飞行（ ）.

A. 8米    B. 10米    C. 12米    D. 14米

解析：作AB⊥BC于点B，连接AC，如图2.

根据题意可得BC = 10 - 4 = 6（米），AB = 8米.

在Rt△ABC中，∠ABC = 90°，

∴AC2 = AB2 + BC2 = 82 + 62 = 100.

∵AC > 0，∴AC = 10. 故选B.

三、水有多深

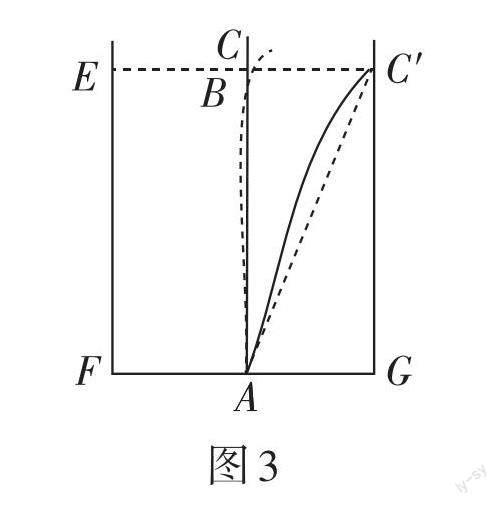
例3 《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深、葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AC生长在它的中央，高出水面部分BC为1尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部C恰好碰到岸边的C'处（如图3），水深和芦苇长各多少尺？则该问题的水深是__________尺.

解析：如图3，设芦苇长AC = AC' = x尺，则水深AB = （x - 1）尺.

∵C'E = 10尺，∴C'B = 5尺.

在Rt△AC'B中，由勾股定理可得方程52 + （x - 1）2 = x2，解得x = 13，

即芦苇长13尺，则水深为12尺. 故应填12.

四、巷有多宽

例4 如图4，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙，顶端距离地面2米，则小巷的宽度为（ ）.

A. 0.7米 B. 1.5米

C. 2.2米 D. 2.4米

解析：先求出AB2，即得到A'B2，再求出BD，由CD = BC + BD即可得结论.

∵∠ACB = 90°，BC = 0.7，AC = 2.4，∴AB2 = 0.72 + 2.42 = 6.25.

∵A'B = AB，∴A'B2 = AB2.

∵∠A'DB = 90°，A'D = 2，BD2 + A'D2 = A'B2，∴BD2 + 22 = 6.25，∴BD2 = 2.25.

∵BD > 0，∴BD = 1.5，∴CD = BC + BD = 0.7 + 1.5 = 2.2（米）. 故选C.

五、路有多短

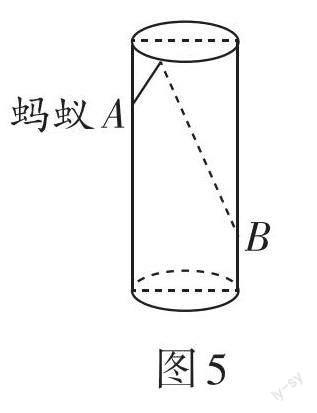
例5 如图5，透明的圆柱形容器（容器厚度忽略不计）的高为12 cm，底面周长为10 cm，在容器内壁离容器底部3 cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3 cm的点A处，则蚂蚁吃到饭粒须爬行的最短路径是__________cm.

解析：如图6，将容器侧面展开，作点A关于EF的对称点A'，连接A'B，根据两点之间线段最短可知，A'B的长度即为蚂蚁吃到饭粒需爬行的最短距离.

过点A'作A'D⊥BD，∵高为12 cm，底面周长为10 cm，点B在容器内壁离容器底部3 cm处，蚂蚁在容器外壁离容器上沿3 cm的点A处，∴A'D = 5 cm，A'E = AE = 3 cm，BD = 12 - 3 + A'E = 12 （cm），A'B2 = A'D2 + BD2 = 52 + 122 = 169 = 132.

∵A'B > 0，∴A'B = 13 cm，即螞蚁吃到饭粒需爬行的最短路径是13 cm.

分层作业

难度系数：★★★ 解题时间：3分钟

在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A处. 另一只爬到树顶D处后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，求这棵树高多少米. （答案见第39页）

（作者单位：江苏省兴化市楚水初级中学）