勾股定理易错点精练

王雪洁

勾股定理是初中数学中非常重要的定理. 在学习勾股定理之前，求边时要根据边元素的已知条件，求角时必须知道角元素，邊角之间好像毫无关系，而有了勾股定理，我们就可以通过边求角，通过角求边. 如此“逆天”的定理，同学们应该好好地盘点一下它的易错点.

一、考虑不全漏解

例1 若一个直角三角形的三边长分别为 a，b，c ，且a2 = 9，b2 = 16，则c2为 .

解析：受惯性思维影响，许多同学习惯性地认为a2 + b2 = c2，却忽略了∠B和∠C都有可能是直角. 当∠C为直角时，c2 = a2 + b2 = 9 + 16 = 25；当∠B为直角时，c2 = b2 - a2 = 16 - 9 = 7. 故应填25或7.

二、忽略定义要求

例2 下列各组数能构成勾股数的是（ ）.

A. 6，8，10 B. 1.5，2，2.5 C. 7，8，15

解析：勾股数的定义有两个方面的要求：一是满足勾股定理，二是所有数据都是正整数. 故应选A.

总的来说，勾股定理是形题数解的主要工具，形式比较简单，只要注意基本定义和分类讨论即可. 其易错点还有可能出在与其他知识点的结合上，因此要灵活运用勾股定理.

三、与其他知识点结合时易错

1. 与圆面积结合

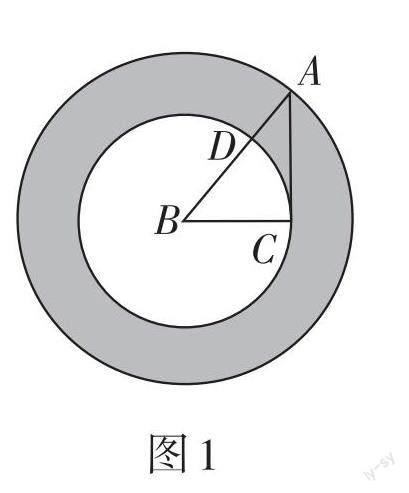
例3 如图1，在△ABC中，∠ACB = 90°，将其绕点B顺时针旋转一周，则分别以BA，BC为半径的圆形成一个圆环（阴影部分），为求该圆环的面积，只需测量一条线段的长度即可，这条线段是（ ）.

A. AD B. AB

C. AC     D. BD

解析：根据题意可知圆环的面积 = π·AB2 - π·BC2 = π（AB2 - BC2）. 在Rt△ABC中，根据勾股定理得到AC2 = AB2 - BC2，因而只要知道AC的长即可. 故应选C.

2. 与全等结合

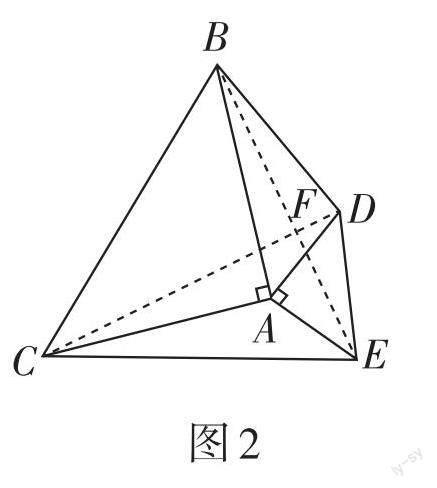
例4 如图2，在等腰直角三角形[ABC]与等腰直角三角形[DAE]中，[∠BAC=∠DAE=90°]，[AB=AC=2]，[AD=AE=1]，则[BD2+CE2]等于（ ）.

A. 9      B. 11

C. 10    D. 12

解析：连接CD，BE，交于点F，易证△CAD≌△BAE，可得CD⊥BE，根据勾股定理可得BF2 + CF2 = BC2，DF2 + EF2 = DE2，BC2 = AB2 + AC2 = 8，DE2 = AD2 + AE2 = 2，则BD2 + CE2 =10. 故应选C.

3. 与轴对称结合

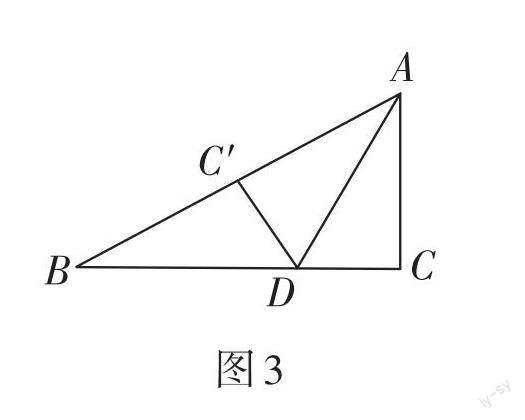
图形的运动只改变图形的位置，不改变图形的形状、大小，运动前后的两个图形全等. 翻折就具备这样的特点. 如图3，将△ABC沿AD翻折，使点C落在AB边上的点C'处，则△ADC≌△ADC'.

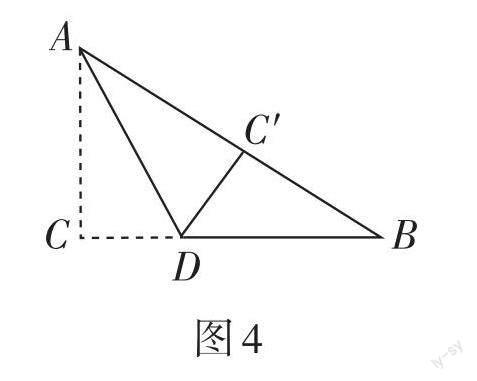
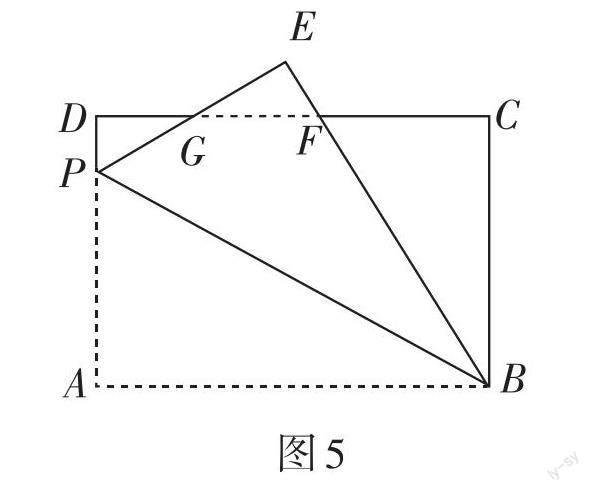
例5 尝试解决：（1）如图4，在△ABC中，∠C = 90°，AC = 6，BC = 8，将△ABC沿AD翻折，使点C落在AB边上的点C'处，求CD的长. （2）如图5，在长方形ABCD中，AB = 8，AD = 6，点P在边AD上，连接BP，将△ABP沿BP翻折，使点A落在点E处，PE，BE分别与CD交于点G，F，且DG = EG. ①求证：PE = DF；②求AP的长.

解析：（1）利用勾股定理求AB，由翻折及三角形全等的性质得到AC = AC' = 6，BC' = AB - AC' = 10 - 6 = 4，再利用勾股定理求出CD = 3；（2）①由翻折可知△PAB≌ △PEB，根据“ASA”证明△DPG≌△EFG，即可得出结论；②先将BF，CF分别用PA表示出来，再根据勾股定理即可求出PA = [24/5].

（作者单位：沈阳市第一四五中学）