轴箱钢簧断裂失效及结构参数优化分析
2023-10-07贺延霖周劲松王腾飞
贺延霖, 周劲松, 王腾飞
(同济大学铁道与城市轨道交通研究院,上海 201804)
引 言
轴箱钢簧是轨道车辆转向架的关键部件,通过对轨道车辆运维数据的调研发现,转向架轴箱钢簧断裂情况愈发频繁,严重影响列车运行安全,且给轨道交通公司维保工作带来较大困扰。
董磊等[1]通过断口微观观察和金相分析等,判定轴箱钢簧断裂属于疲劳失效。张顺等[2]通过动力学建模和仿真分析,得到了钢簧断裂工况下列车动力学各项性能指标,研究结果表明在钢簧断裂的情况下,车辆的运行安全性会恶化。Wang K等[3]通过振动响应角度分析钢簧失效的原因,并提出镟轮、更换新参数钢簧等措施。
轴箱钢簧断裂失效分析的相关文献较多,但很少分析改进措施合理性和优化效果,故本文针对车辆一系轴箱钢簧断裂失效问题开展相关研究,分析其断裂原因并针对钢簧结构参数改进提出合理建议,验证优化方案合理性同时对比分析优化效果。
1 钢簧断裂情况调研及断口分析
某型地铁车辆在服役过程中,其轴箱钢簧会受到交变载荷的作用而频繁发生断裂,对该地铁公司运维数据调研后发现,该车型车辆TC车的轴箱钢簧断裂次数最多,如图1所示,且断簧时最后一次镟轮后里程平均值为14.5万公里,最大值高达23万公里,车轮状况普遍糟糕。

图1 断裂钢簧所处车辆统计图Fig.1 Statistical diagram of the vehicle where the broken steet spring is located
对轴箱钢簧断口进行宏观分析,如图2所示。其断裂位置位于支撑圈和有效圈的过渡处, 断裂面与弹簧轴线呈45°角;在表面挤压流变区,可见表层组织受挤压变形,并斜向开裂,表明钢簧断裂前承受的载荷较大。

图2 钢簧断裂外观Fig.2 Fracture appearance of steel spring
断面情况如图3所示。从图3可以观察到断口无明显塑性变形,断面存在疲劳源区、疲劳扩展区和瞬断区,疲劳源位于贝纹线收敛中心[4],该区域颜色较深,有氧化锈蚀物覆盖。此外,裂纹起源于钢簧下表面,结合表面挤压流变区形貌分析,该断面为碾压形断面。

图3 钢簧断面宏观形貌Fig.3 Macro-morphology of steel spring cross section
通过高倍率微观断口测试,可见多条斜向平行分布的细裂纹,曲折发展,如图4所示。综合宏观和微观分析结论,钢簧断口属于接触疲劳断口,该一系轴箱钢簧断裂为典型的疲劳失效[5]。其中,疲劳损伤具有累积性质,疲劳失效是长期累积的结果,且疲劳具有非线性增长特点,即随着运行里程数增加,疲劳损伤值呈现指数形增长[6]。

图4 断面微观测试结果Fig.4 Microscopic test results of cross section
2 钢簧断裂原因分析及动力学模型建模
通过数据调研和现场勘察发现,断簧车辆距最后一次镟轮的运营里程皆为15万公里左右,且断簧处车轮状况普遍较差,如图5所示,断簧处车轮表面出现擦伤,此时车轮径跳值变大;此外,通过现场测试后发现轨道状态良好。

图5 断簧处车轮表面擦伤Fig.5 Abrasion on wheel surface at spring break
由以上分析可知,车轮激励可能加剧钢簧的振动响应。为此,针对弹簧及车轮开展了多项测试,包括弹簧模态测试、车轮状况测试及振动加速度测试等。
2.1 钢簧断裂原因分析
使用车轮不圆度测试仪对断簧整车车轮进行测试,如图6所示。测试得到整列车各车轮的多边形幅值,并求取各车轮多边形幅值平均值,如图7所示,断簧处车轮多边形幅值高于整车平均水平,尤其是10阶多边形,幅值较大。

图6 车轮状态测试Fig.6 Wheel condition test
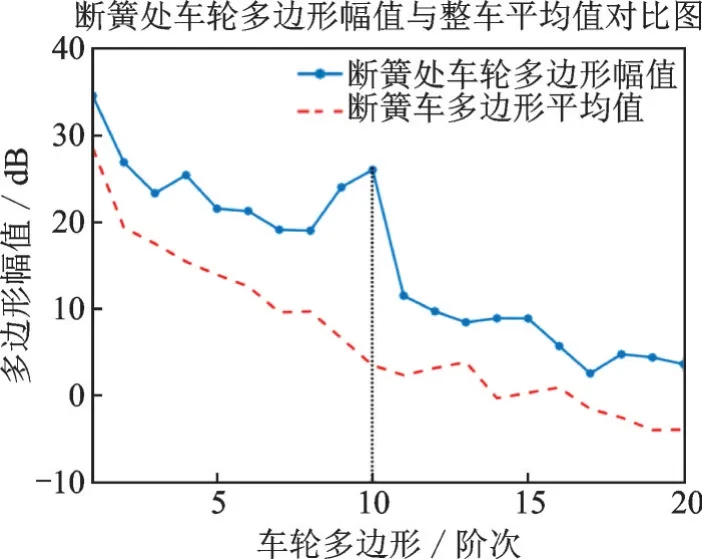
图7 车轮多边形幅值图Fig.7 Amplitude diagram of wheel polygon
车轮多边形的激励频率f的计算公式如下:
式中V为车辆运行速度,N为多边形阶数,D为车轮有效圈直径。基于实测数据,列车速度稳定在73 km/h左右,车轮有效圈半径为410 mm,计算得到车轮10阶多边形的激励频率为78.7 Hz。
弹簧模态测试结果如表1所示,弹簧的一节固有频率为77.5 Hz,与车轮多边形激励频率相近。
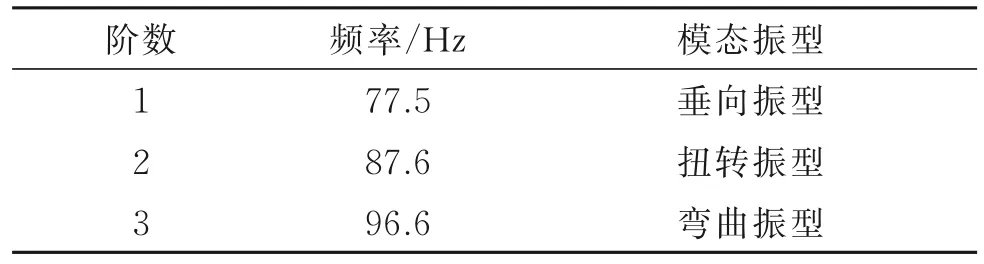
表1 弹簧模态测试结果Tab.1 Spring mode test results
对轴箱和弹簧振动加速度测试结果进行频谱分析,如图8所示。图8(a)为不同工况下镟轮前后轴箱加速度对比图,可以看出镟轮后轴箱加速度主频如65,72.5,78.3 Hz(10阶多边形激励频率)的幅值都有了明显的降低,表明镟轮后弹簧所受激励明显减小。图8(b)表明断裂钢簧的一阶固有频率78.2 Hz被激起,镟轮后主频幅值明显降低。综合以上分析可知,车轮多边形演化过程中10阶多边形幅值增大,在78 Hz处产生较大的激励,与钢簧的一阶模态频率接近,引起了结构共振,放大了钢簧的主频幅值,导致钢簧产生疲劳断口,进而发生断裂失效现象。
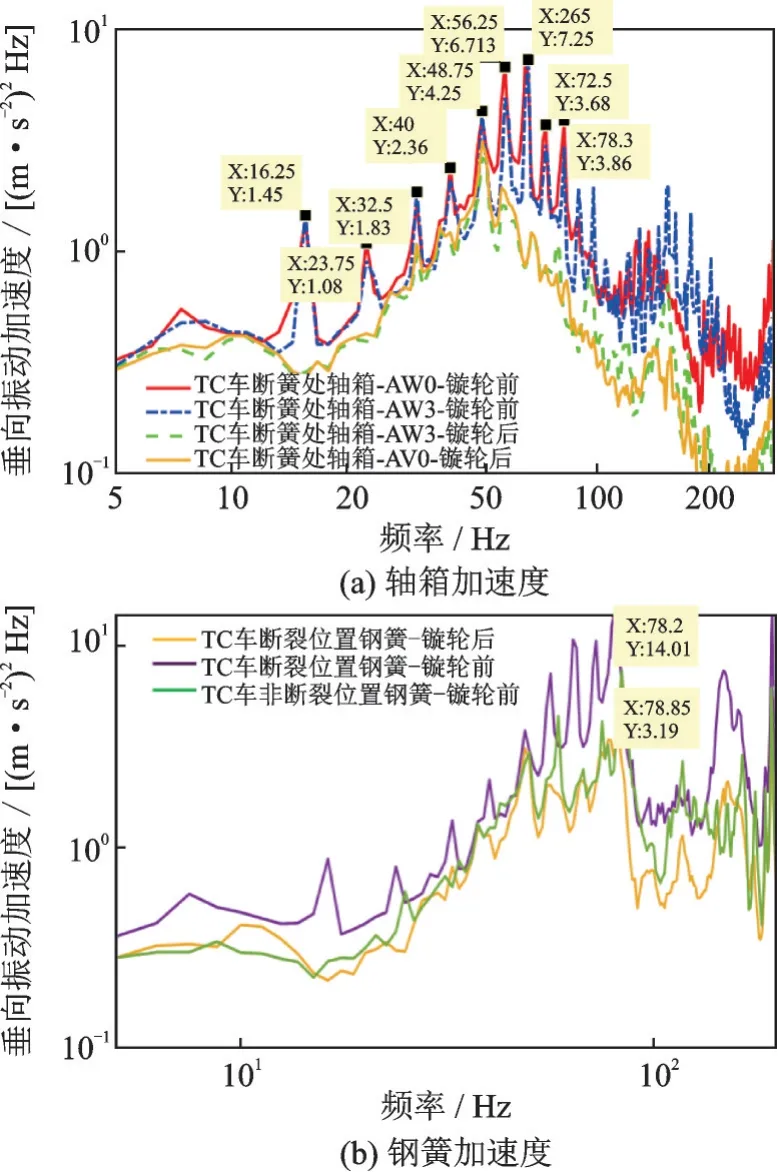
图8 垂向振动加速度频谱图Fig.8 Vertical vibration acceleration spectrum
2.2 刚柔耦合多体动力学建模
为研究优化方案的优化效果,基于ANSYS和SIMPACK联合仿真,通过输入柔性体和应力文件建立了能提取钢簧动应力的车辆刚柔耦合多体动力学模型,其中车体、构架等结构为纯刚体,钢簧为柔性体,如图9所示。

图9 整车刚柔耦合动力学模型Fig.9 Vehicle rigid-flexible coupling dynamics model
为验证建模的准确性,对比了钢簧的模态结果,如表2所示,实测和仿真中钢簧各阶模态频率和振型都匹配,模态频率误差最大为0.02%;此外还对比实测和仿真轴箱PSD图,如图10所示,表明建立的刚柔耦合动力学模型通过验证
3 轴箱钢簧结构参数优化分析
为避免钢簧产生较大疲劳损伤提前失效,除定期镟轮、打磨钢轨以此来降低轮轨激励的方案外,还可以对弹簧的结构参数进行优化,改变钢簧的固有频率,使其远离车轮多边形激励频率,避免产生结构共振。
钢簧的结构参数包括簧丝直径、钢簧中径和有效圈数等,其与钢簧所受切应力关系式如下:
式中τ为切应力;P为一系悬挂系统载荷(实测时域信号);C为螺旋比;d为簧丝直径;R为钢簧中径,在车辆一系悬挂系统载荷已知情况下,钢簧切应力的大小值与有效圈数a无关。对得到剪应力时域曲线进行雨流计数,并根据Miner损伤累积理论计算疲劳损伤D,如下式所示:
基于皮尔逊相关系数法对抽取大样本中的结构参数与疲劳损伤进行敏感性分析,其中样本结构参数有效圈数、簧丝直径、钢簧中径的范围分别为3.3~4.3,194~214 mm,33~43 mm,计算公式如下:
式中ρ为相关系数,x与y分别代表要判断相关性的两列数据。将有效圈数a,簧丝直径d,钢簧中径R分别带入式(4)中,得到钢簧结构参数与疲劳损伤的关联性,如表3所示。簧丝直径与疲劳表现出负相关,需要增大簧丝直径,降低钢簧中径,减小疲劳损伤。有效圈数与疲劳损伤相关性不大,可根据其他限制因素(钢簧高度)确定优化后的有效圈数。
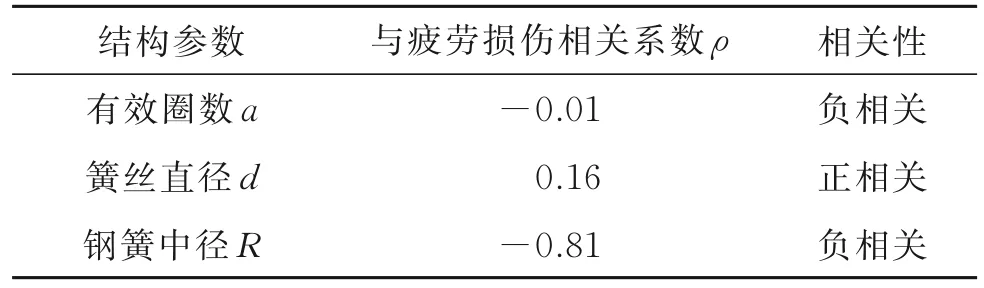
表3 钢簧结构参数与疲劳损伤关联性Tab.3 Relationship between structural parameters of steel springs and fatigue damage
综合以上分析提出了一组钢簧新结构参数,如表4所示。
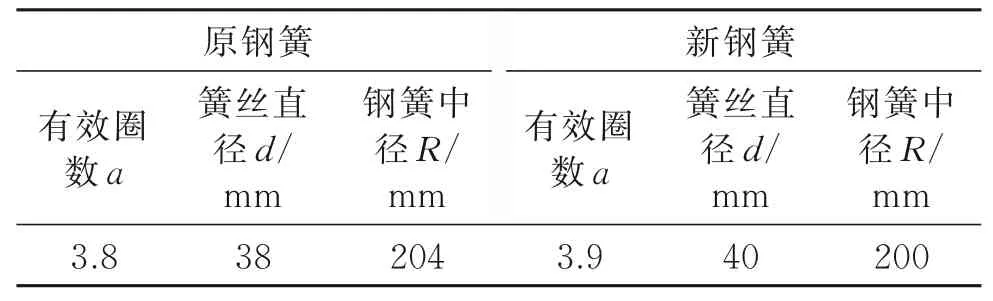
表4 钢簧新旧参数对比表Tab.4 Steel spring old and new parameters comparison table
4 钢簧更新优化效果验证及动力学性能对比分析
更换新结构参数钢簧后,其刚度由640 N/mm上升到810 N/mm,分别从钢簧的模态、所受动应力以及整车动力学性能等方面验证方案的合理性,并分析优化效果。
4.1 钢簧模态及动应力对比分析
新结构参数钢簧的模态参数如表5所示。新结构参数钢簧各阶振型未改变,而模态频率变大,一阶模态频率为97.1 Hz,避开了车轮演化过程中多边形幅值较大的激励频率。

表5 钢簧模态对比表Tab.5 Steel spring mode comparison table
在刚柔耦合动力学模型中输入相应的轨道谱和车轮数据,得到钢簧更换前后动应力时域和频域图,如图11所示,时域信号中新的钢簧动应力明显降低,频域上新钢簧的动应力主频幅值明显降低,优化效果明显。
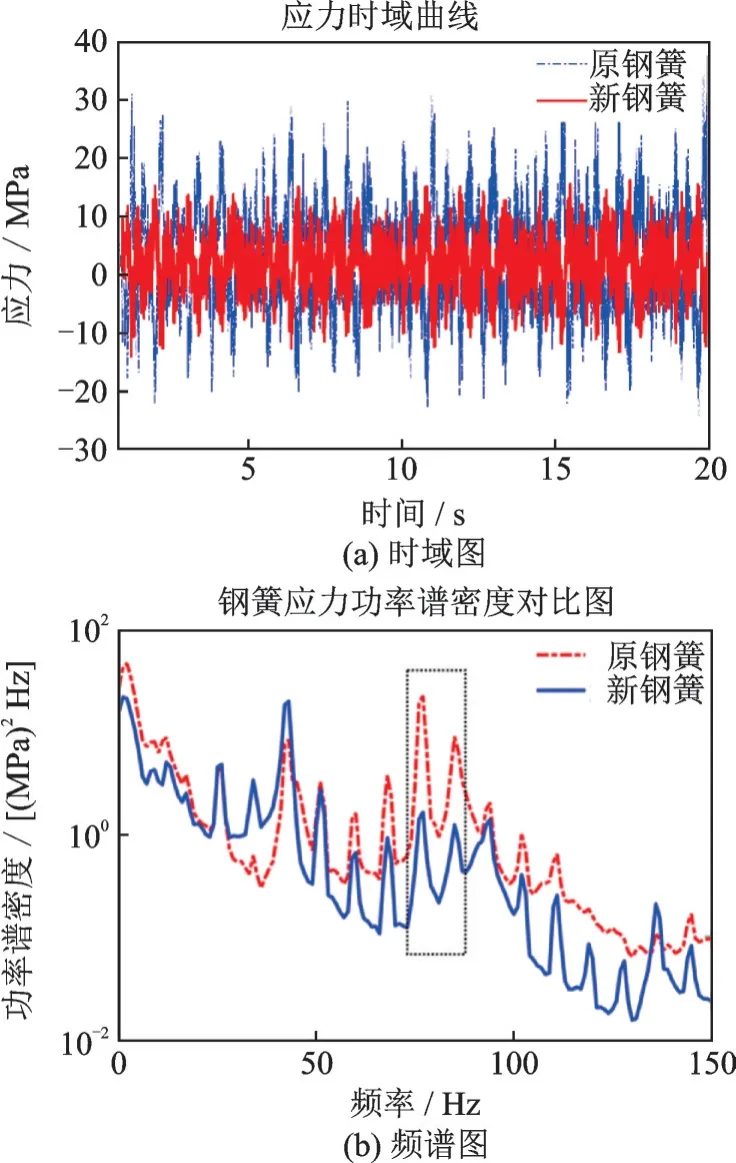
图11 钢簧更换前后动应力对比Fig.11 Comparison of dynamic stress before and after steel spring replacement
4.2 整车动力学性能对比分析
依据GB/T 5599的规定[7],对更换钢簧前后的整车动力学性能进行对比评定,其中的动力学指标及计算方法如下:
(1) 脱轨系数Q/P
当曲线半径大于400 m时:
当曲线半径小于等于400 m且大于等于250 m时:
式中Q为车轮作用于钢轨上的横向力,P为车轮作用于钢轨上的垂向力。
(2) 轮重减载率ΔP/P
当速度小于等于160 km/h时:
式中 ΔP为轮重减载量为增载和减载侧车轮的平均轮重。
(3) 轮轴横向力
轮轴横向力H为:
式中P0为静轴重,P0取值36.97 kN,计算出H的限值为39.64 kN。
(4) 运行平稳性指标W
基于Sperling指标,平稳性指标限值W如表6所示。

表6 平稳性指标等级表Tab.6 Stationary index ranking table
动力学性能计算曲线半径设置为450 m,仿真计算得到钢簧优化前后整车动力学指标,如表7所示。结果显示更换新钢簧后,脱轨系数、轮重减载率和平稳性指标上升,轮轴横向力降低,各项动力学指标都满足设计要求。
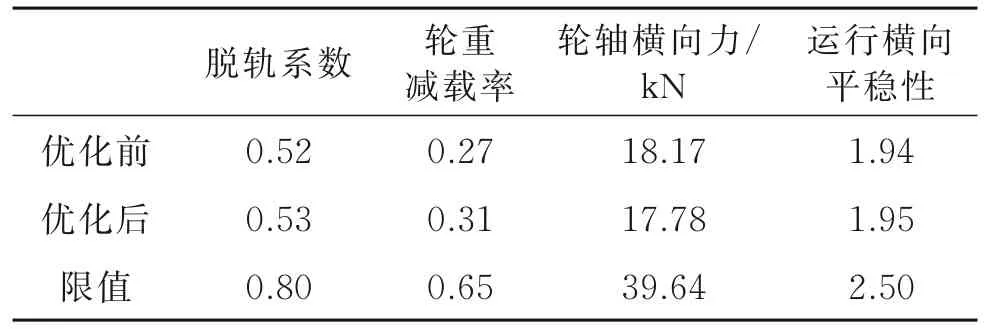
表7 整车运行安全性、平稳性指标Tab.7 Vehicle running safety, stability index
5 结 论
本文基于断口分析和试验测试,探究一系轴箱钢簧断裂失效原因,并根据仿真计算结果,分析了钢簧更换前后各项性能指标,得到以下结论:
(1)钢簧由于承受车轮多边形激励而产生疲劳裂纹进而断裂失效,同时车轮10阶多边形幅值较大,且主频与钢簧固有频率相近,引起结构共振,加剧了钢簧振动响应,使钢簧在生命周期内提前失效,减少了钢簧使用寿命。
(2)基于皮尔逊相关系数法提出了钢簧新的结构参数,其一阶固有频率为97.1 Hz,避开了幅值较大的激励频率,使钢簧的振动响应能量减小,疲劳损伤降低。
(3)基于刚柔耦合多体动力学模型,对比分析了钢簧更换前后的整车动力学性能指标,包括脱轨系数、轮重减载率、轮轴横向力以及平稳性指标在内的各项动力学指标都满足设计要求。
