基于多模型网络的激光末制导炮弹诸元解算方法
2023-10-07刘畅雷红波林时尧范世鹏王江
刘畅, 雷红波, 林时尧, 范世鹏*, 王江
(1.北京理工大学 宇航学院, 北京 100081; 2.北京理工大学 中国-阿联酋智能无人系统“一带一路”联合实验室, 北京 100081;3.中国兵器科学研究院, 北京 100089)
0 引言
半主动激光末制导炮弹是一种由火炮发射、在末端利用激光导引头捕获目标并对低速目标进行精确打击的制导弹药[1],由于集常规火炮的低成本与导弹的精确打击能力等优点于一身,得到现代陆军炮兵的广泛应用[2]。为在末制导作用时捕获目标,目前使用射表来确定射击诸元,其中表尺(射角)、程装(惯性陀螺解锁时刻)、延时(激光照射器开始照射的时间)为基本诸元,修正诸元是对气象偏差(包括气压、气温、风向、风速)等进行修正[3]。诸元解算是否合理,关系到分系统能否正常工作(能否成功捕获目标、有限修正能力能否满足需求以及惯性陀螺是否发生碰框),直接影响弹药的命中概率。
针对传统射表应用插值法求解射击诸元精度不高、解算速度慢、无法准确处理精准的分层实时气象信息等问题,学者们在射表编制理论、射表数据采集、射表射击试验等方面做出了诸多贡献,提高了命中概率。赵明阳等[4]为精确计算气象对诸元的影响,应用贪心优化算法对气象修正表自动分区并计算拟合系数,逼近函数系数精确度较高,实现了自动分区拟合的功能。褚进等[5]对高原条件下某型末制导炮弹弹道进行仿真分析,对比了不同诸元对名义弹道及捕获域的特点,为高原射表编拟提供了参考。丁天宝等[6]为改进以实弹射击为主的射表编制方法,提出了高原与平原交接阶梯抑制方法,减小了平原与高原射表在高度交接段的原理误差,适用于宽海拔作战任务。陈瑞军等[7]针对基本诸元解算速度慢、不能满足有效攻击区的战术指标、命中率低的问题,提出了简化的弹道模型并应用攻击区中心为表载射程的解算方法,提高了制导弹药射表的编制精度。贾波等[8]对气动参数进行灵敏度分析并进行辨识,给出了基于弹道精确测量的射表编拟方法。
然而,目前基于传统射表的诸元解算存在以下问题:
1)射击诸元与弹道参数存在强非线性的映射关系,本质上是一个复杂的多因素耦合问题。目前通过线性插值法求取,会带来较大的截断误差。
2)若将实时获取的分层气象信息作为输入,则其维度大大增加,射表规模随之显著增大,且插值计算量较大,难以满足快速计算需求。
3)目前虽有一些基于传统射表的射击诸元计算软件,但忽略诸元相关的因素较多,求解精度差。
随着人工智能技术的不断发展,诸多学者将其应用在弹道解算的问题中。文献[9]应用深度神经网络,将升力、阻力系数等作为输入,将预期落点作为输出,解决了故障条件下高超飞行器容错制导问题。文献[10]为解决空空导弹无法同时解算多种攻击区的规划及解算问题,提出了深度拟合网络模型及训练策略,相对于传统方法提高了解算的准确性及实时性。文献[11]针对弹道轨迹预测精度不足的问题,构建混合输出单元,应用增强上下文信息长短期记忆模型进行预测,结果表明该方法相对于传统方法在实时性及泛化能力上均有较大优势。文献[12]应用卷积及长短期记忆混合神经网络,解决了弹丸非线性轨迹预测问题;应用龙格-库塔法解算6自由度弹道模型得到大量样本,应用混合网络模型对轨迹进行预测,结果表明在预测精度上优于单一的网络模型,为轨迹预测提供了一定的参考。
本文针对快速精确求取射击诸元的实际需求,利用神经网络在表达映射关系及求解非线性拟合问题上的优势,提出一种基于多模型网络的诸元解算方法,使诸元解算求解精度更高。该诸元解算方法的主要创新点为:1)可对实时气象进行分析,并将其作为多模型网络的输入,相对于仅考虑地面气象或标准气象,精度更高;2)将诸元解算这类多因素耦合问题进行功能解耦,使多模型网络中的个体仅需实现单一功能,改善了各网络的可解释性与求解精度,大大降低了网络优化与设计的复杂度。
1 弹道模型及气象分析
1.1 激光末制导炮弹弹道模型
激光末制导炮弹由无控段、程控段及末制导段组成,程装及延时是各段之间转换的重要标志。若炮弹仅以无控及程控段飞行,则此时的落点称为名义落点。激光末制导炮弹弹道如图1所示。

图1 飞行轨迹图
对于弹道轨迹,通常采用非线性6自由度模型描述弹道[13],气动特性由风洞实验获取。非线性6自由度弹道模型通常由质心动力学方程、绕质心转动动力学方程、质心运动学方程、绕质心转动运动学方程及几何关系等构成[14]。建立的微分方程组[15]如下:
(1)
(2)
(3)
(4)
式中:m为弹丸实时质量;vm、θ、ψv分别表示弹丸速度、弹道倾角及弹道偏角;wx、wy、wz表示速度在弹体坐标系下的转动角速度分量;x、y、z表示弹丸在地面坐标系下的3个位置分量;ϑ、ψ、γ表示俯仰角、偏航角及滚转角;p为弹丸所受的推力;α、β分别为攻角和侧滑角;Fx、Fy、Fz分别为弹丸受到的阻力、升力及侧向力;g为重力加速度;γv为速度倾斜角;Jx、Jy、Jz分别为弹丸在弹体坐标系下沿3个坐标轴的转动惯量;Mx、My、Mz分别为弹丸在弹体坐标系下沿3个坐标轴的力矩。相关坐标系、力和力矩的定义见文献[16]。其中,角度几何关系如式(5)所示:
(5)
本文暂不考虑末制导段,后续建立样本时仅以名义落点作为期望射程,其原因为:1)当名义落点与实际期望落点相差较小时,依靠弹丸的过载能力可对较小的偏差进行修正,精确命中目标;2)若考虑末制导段,则由于弹丸具有一定的过载能力,会出现基本诸元对应多个射程的情况,此时会出现奇异;3)射表编拟时,同样采用名义落点作为期望射程。因此,合适的基本诸元(表尺、程装)对命中目标有着关键性的作用。
当给定程装、表尺、初速等初始条件时,应用4阶龙格-库塔法对式(1)~式(4)的6自由度微分方程组进行求解,可得到对应的弹道轨迹。其余条件不变,表尺及程装的变化对弹道轨迹的影响如图2 所示。
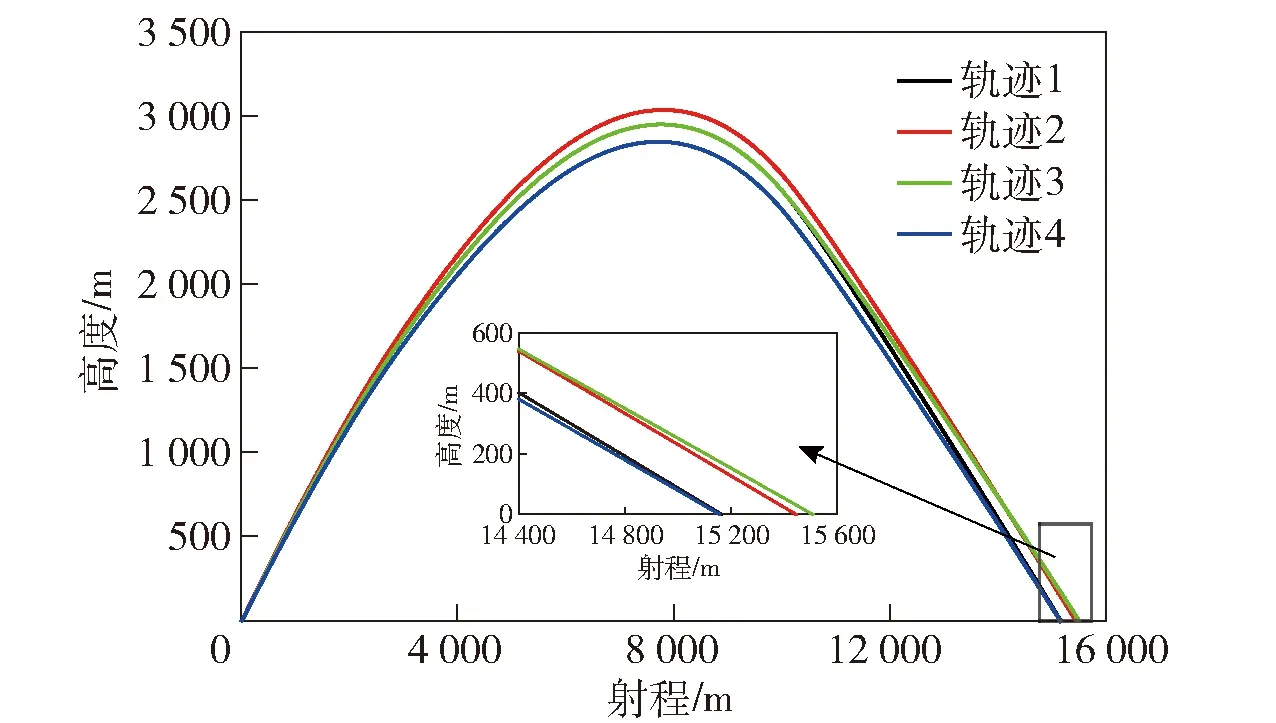
图2 弹道轨迹
由图2可见:轨迹1和轨迹2的程装相同,轨迹2的表尺大于轨迹1,可以看出轨迹2的射程大于轨迹1;轨迹1和轨迹3的表尺相同,轨迹1的程装大于轨迹3,轨迹3的射程大于轨迹1;表尺和程装对射程的影响较大。表尺即为微分方程组的初始弹道倾角θ0;程装即惯性制导段的初始时刻Tcz,此时弹上惯性系统开始工作,通过重力补偿使弹丸基本按照直线飞行,其目的为增大射程及以较小的速度倾角进入末制导。由此可知升力Y变化为
(6)
由式(6)可以看出,程装对微分方程中的升力影响较大,可见程装变化对射程影响较大。
图2中轨迹1与轨迹4射程相近,但二者表尺和程装大小均不相同,因此无法单一从某个参数判断诸元对射程的影响,表明诸元解算是一个多维度耦合问题。
1.2 气象条件分析
气象条件的精确分析对弹丸的射击精度有着决定性影响,因此对气象条件进行充分的分析是非常必要的。其中,气压、气温、风向及风速对弹道的影响较大,下面对其进行逐一分析。
1.2.1 气温分析
气温及气压主要对马赫数有很大影响,式(1)~式(4)中的升力系数等均与马赫数有关。目前,都是通过简易或精密分析方式处理气温。简易法是假定当前环境符合标准气象环境,即气温按线性变化,变化趋势如式(7)所示:
τ=τ0-Gy
(7)
式中:τ0为地面气温,τ0=299.8 K;G为气温变化系数,G=6.328×10-3。从式(7)中可以看出,在采用上述方法进行气温简易计算时,需要假设气温变化趋势是恒定的,但实际中气象情况复杂,标准气象的线性变化假设与实际情况有较大差距。精密气象是测量不同弹道层下的气温,虽然此方法精度较高,但计算较为复杂,且每层间的温度按线性插值求得。若要对气温进行精确分析,则需使用实际气温。以我国某地区近4年6~7月份为例,其温度变化曲线如图3所示。

图3 气温变化趋势
由图3可以看出,相同地区相近月份的气温变化趋势是类似的,因此可以将相近月份的气温进行非线性拟合。应用此方法不仅可以对实际气温进行分析,得到比线性方法更高的拟合精度,而且计算量相比于传统高精度计算方法计算量更小。
1.2.2 气压分析
与气温分析类似,以相同地区近4年6~7月份为例,其温度变化曲线如图4所示。
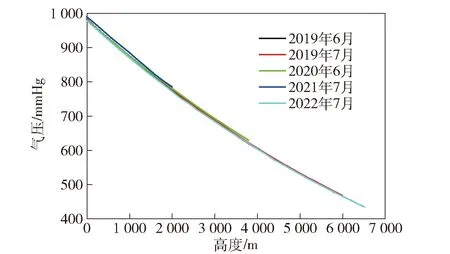
图4 气压变化趋势
由图4可以看出,相同地区相近月份的变化趋势一致性较好,同样可以对气压进行拟合处理。
1.2.3 风向及风速分析
风对弹道的影响主要是引起附加攻角Δα及侧滑角Δβ,使得在求解弹道轨迹时,在攻角和侧滑角的基础上还需要考虑附加角度。传统射表不考虑风的影响,然而实际射击中,风对方向及射程的影响较大。为便于分析修正,通常采用弹道平均值的方法,即求得一个恒定的平均风代替实际风。由于风在不同弹道层的影响不同,各层风所赋的权重(层权)不同。根据风向和风速可将风分解为横风(垂直于弹道方向)及纵风(平行于弹道方向)。两者求取层权的方式相似,因此以纵风为例进行求取层权的说明。
设弹道高分为n层,首先假设全弹道均有相同的平均纵风,计算出相对于无风状态下的射程偏差xw;其次计算出第1层无风状态下的射程偏差xw1,此时风偏在第1层所起作用x1大小为
x1=xw-xw1
(8)
依次类推,可求出每层所起作用大小xi,进而可得每层的层权为
Qi=xi/xw
(9)
式中:Qi为每层的层权。于是可得弹道纵风为
(10)
式中:xwind为恒定的平均纵风;xi,wind为每层的实际纵风。若要求取准确的层权,则不仅需要考虑射程,还需要考虑初始速度、初始弹道倾角、气动参数等,而传统方法中的多维插值计算量较大,难以满足快速计算需求;若计算时仅考虑射程影响,则无法求取精确的层权。因此,如何在多维参数影响下求取层权,对分析风的影响是至关重要的。
2 基于多网络的诸元解算模型
2.1 多模型网络分析
由第1节分析可知,所需解决的问题为:
1)如何对气温、气压进行拟合。拟合完毕后,仅将参数作为网络模型的输入即可,在保证精度的同时减小计算量。
2)不考虑风的影响,如何求解基本诸元。将气温、气压的拟合参数及期望射程作为网络模型的输入,可输出表尺及程装。
3)当有风干扰时,在考虑多方面因素下,如何快速准确地求出弹道的平均风(包括横风及纵风)。
4)求出平均风后,如何对基本诸元修正,获取实际诸元。
通过第1节分析可知,诸元解算作为一个耦合问题,其输入输出之间存在一定的映射关系,神经网络在解决映射及非线性拟合问题上有明显的优势,因此可应用神经网络解决此问题。另一方面,通过上述分析可知,各个问题之间存在一定的耦合关系,无法将所有问题通过单一的网络求解,因此本文提出一种基于多模型网络的诸元解算方法。本文求解框架如图5所示。
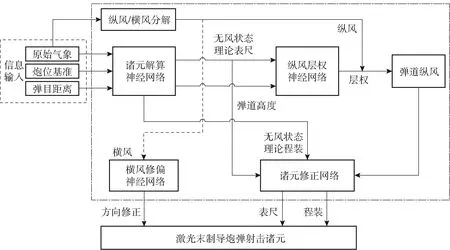
图5 模型整体框架
由图5可以看出,多模型网络的流程为:
步骤1将实际气象中的气压、气温进行拟合,将拟合参数、期望射程等作为诸元解算神经网络的输入,输出为对应的表尺、程装、弹道高度。建立样本后,对该网络进行训练。
步骤2将诸元解算神经网络输出的无风状态下的表尺及弹道高度作为纵风层权神经网络的输入,输出为对应的层权,再将实际的风向、风速与层权按式(10)进行计算,求得平均弹道纵风。
步骤3与步骤2类似,可求得平均弹道横风,再根据横风及射程大小得到方向修正量。
步骤4将得到的平均弹道纵风作为诸元修正网络的输入,将表尺的变化量作为输出,将变化量与步骤1得到的表尺相加,得到实际表尺。由于表尺、程装之间存在耦合,仅考虑变化表尺。
根据上述步骤,得到的表尺、程装及方向修正量即为诸元解算的最终结果。
2.2 样本建立
各网络模型的样本建立类似,因此以诸元解算为例进行说明。由于实际飞行实验数据较少,无法构建大量样本,可根据实际飞行数据对仿真中的气动参数进行拟合。应用拟合后的参数进行仿真,得到大量样本,此时获得的样本与实际飞行试验数据相近,诸元计算精度高。
2.2.1最小二乘法及样本建立
由1.2.1节及1.2.2节分析可知,相同地区相近月份气温、气压的一致性较好,因此可将相近月份如每间隔两个月进行参数拟合。以气压为例,将测得的实际气压作为若干离散点,坐标分别为(y1,p1), (y2,p2),…,(yi,pi),…,(yn,pn),通过最小二乘法中的线性回归法[17]拟合。线性回归法主要是通过最小化误差的平方和,寻找最佳的函数匹配。对实际气压的误差εi及残差i的求取如式(11)、式(12)所示:
(11)
i=pi-i
(12)
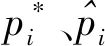
(13)
拟合函数形式如式(14)所示:
g=0.989 8e-0.123y
(14)
根据式(14)进行拟合后,J2即误差平方和为0.003 026,R-square为0.998 9,由此可看出应用式(14)的拟合效果较好,因此仅需将[0.989 8,-0.123]T作为气压输入即可,其余月份方法类似。气温的拟合方法相同,不再赘述。
本文以某型激光末制导炮弹为例,其理论初速与装药号有关,为相应定值。因此以初速为585 m/s为例,初始参数表尺(单位为密位,6 000 mil为360°)和程装(单位为分划,1分划=0.2 s)的采样范围如表1所示。

表1 参数的采样范围
其余初始参数不变,为实际发射条件,此时环境为无风状态。根据不同初始条件,对式(1)~式(4)的6自由度弹道方程进行求解,即可得到对应的弹道轨迹。气动参数已经根据实际飞行数据进行了拟合,可保证仿真结果与实际飞行弹道相近。通过表1的采样间隔共生成1 050条弹道,实现对实际飞行轨迹的高泛化度覆盖。
2.2.2 网络训练
神经网络是一种具有很强非线性拟合能力的数学方法,可以解决一些传统推理模型无法解决的问题[18]。通过提取、学习和训练数据中的隐藏模式,并调整每个节点的权重,神经网络的输出值趋于预期输出。本文采用深度神经网络[19](DNN)对模型进行训练。由于本文采用多模型网络进行拟合,每个网络仅需要解决单一简单问题,大大降低了网络设计复杂度,因此本文设计的DNN仅使用2个全连接层作为隐藏层,每层有10个神经元。以诸元解算神经网络为例,其结构如图7所示。
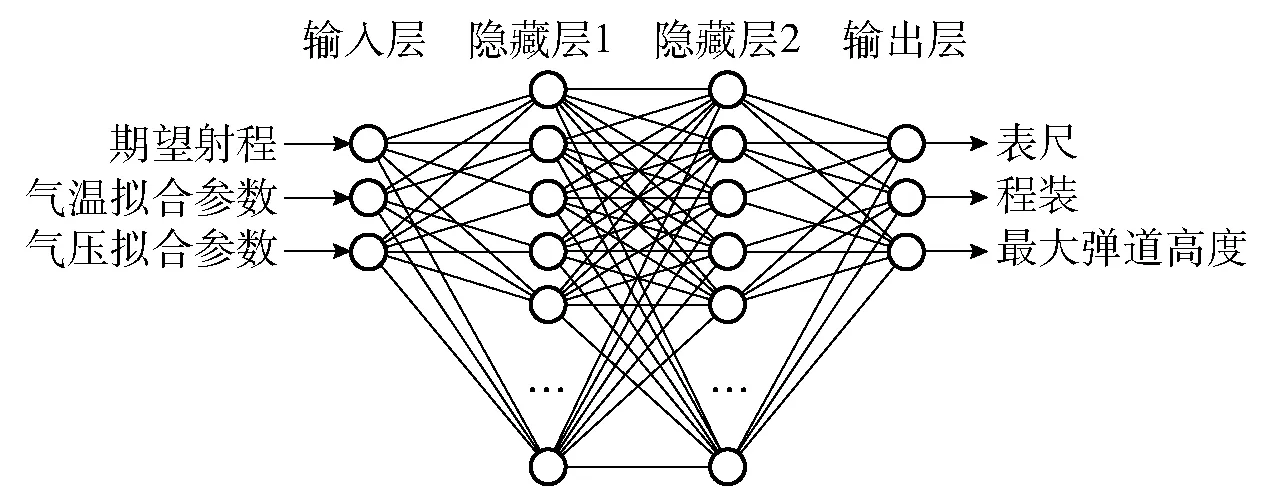
图7 DNN网络结构
由图7可知,本文所设计的DNN包括输入层、隐藏层和输出层,其中,输出层为表尺、程装、最大弹道高度,输入层数据为期望射程、气温及气压拟合参数。两个相邻层之间的数据传输以权重的形式进行。
神经元的数学模型如式(15)所示:
(15)
式中:σ为神经元的输出;f(·)为激活函数;di为第i个神经元的输入;ωi、δ为对应神经元的权重及阈值。本文采用ReLU作为输入层和隐层的激活函数,具有简化计算过程、防止梯度消失及训练网络快速等优势,输出层不设置激活函数,其表达式为
f(d)=max(0,d)
(16)
式中:d为当前神经元的输入。
本文选择表尺、程装、最大弹道高度等期望输出值与实际输出值的最小均方差作为损失函数,如式(17)所示:
(17)
(18)
对于式(18),根据链式法,有
(19)
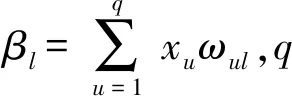
(20)
DNN的训练过程实际上就是通过上述反向传播和梯度下降算法不断优化网络参数,使误差平方和最小化。当误差达到预期时停止对式(20)更新,完成训练。采用ADAM优化器[20]对E(σ,)进行优化,优化后的参数为
(21)
式(18)和式(21)中的学习率为训练预设初值,在DNN训练过程中ADAM优化器会自适应调节该参数。
本文训练过程基于TensorFlow-1.13.0-GPU版构建DNN模型,显卡型号为RTX3060 12G,学习率选取0.001。以诸元解算神经网络为例,根据2.2.1节中得到的1 050条弹道,按照92%的数据作为训练集、4%的数据作为测试集、4%的数据作为验证集的比例,对网络进行离线训练、测试及验证。当网络精度达到预设要求时训练结束。
3 基于多网络的诸元解算模型验证
为验证多模型网络的精度,本节给出诸元解算的数值仿真实验。首先根据验证集的效果论证多模型网络的精度;其次选取3组不同的期望射程及实际气象,将其输入模型中进行验证;再次进行蒙特卡洛仿真实验,进而论证模型的精度及鲁棒性;然后与射表解算出的诸元进行对比,论证模型求解精度更高;最后,通过实际打靶论证本文提出的模型在实际飞行试验中同样适用。
3.1 多模型网络精度
根据第2节1 050条弹道中4%、4%的数据作为验证集、测试集,即分别有42条弹道作为验证及测试,训练中损失函数的变化情况如图8所示。
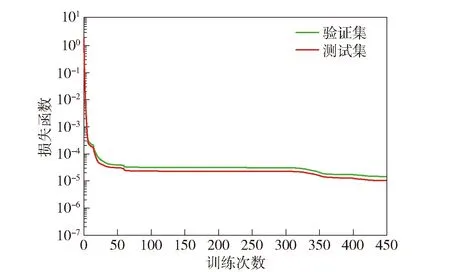
图8 损失函数变化
设定训练1 000轮或损失函数值小于0.000 01为终止条件,由图8可以看出,当训练轮数到453时,已经达到期望的损失函数值。通过上述变化情况可以看出,DNN损失值下降迅速,在第60轮前下降较为迅速,后续变化较为平稳,因此可以说明网络已收敛。使用测试集测试训练好的神经网络,以诸元解算模型中的程装为例,其效果如图9所示。

图9 测试集精度
由图9可以看出,模型预测的程装值与实际程装值相近,绝对误差为0.031 9,均方误差为0.002 9,由此可见训练完毕的诸元解算模型精度较高。
3.2 多模型网络验证
为方便分析验证,初速选取585 m/s,其余仿真条件如表2所示。
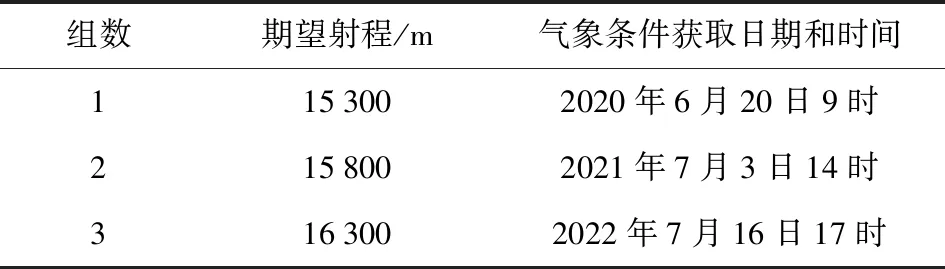
表2 仿真条件
3.2.1 验证诸元解算网络模型
在暂时不考虑风的情况下,将3组期望射程及气温、气压拟合的参数作为模型输入,对模型输出得到表尺及程装进行验证,结果如图10所示。

图10 诸元解算模型输出结果
由图10可见,模型输出射程与期望射程相近,具体误差及精度如表3所示。
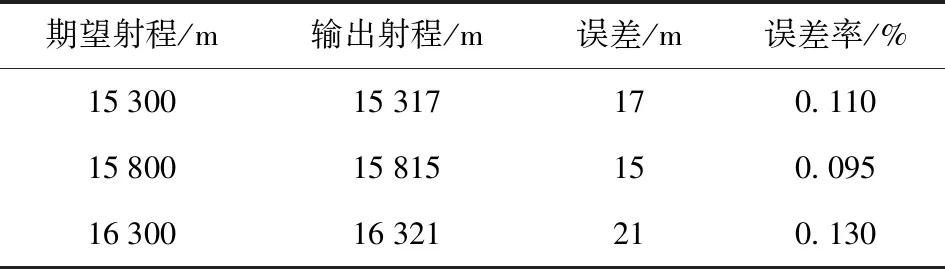
表3 误差与精度
由表3可知,3组期望射程下误差值在20 m附近,误差率在0.1%附近,由此可进一步论证诸元解算网络的精度较高。
3.2.2 验证纵风及横风修正网络
以纵风修正网络为例,将诸元修正网络输出的弹道高度及期望射程作为输入,输出为纵风层权。如期望射程16.3 km时,将弹道高度按400 m分层,分为10层,纵风层权神经网络输出的层权为[0.035 294,0.070 588,0.070 588,0.082 352,0.129 411,0.141 176,0.105 882,0.2,0.164 705,0],将纵风层权及实际风速代入式(10)中,可得平均纵风为7.855 6 m,平均横风获取方式相同。
3.2.3 输出修正后的诸元
将平均横风、纵风与期望射程输入诸元修正网络,经过修正后的诸元结果如图11及表4、表5所示。
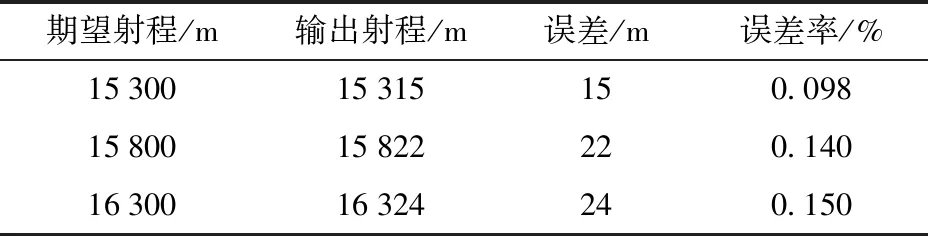
表4 期望射程的误差与精度

表5 横偏的误差与精度
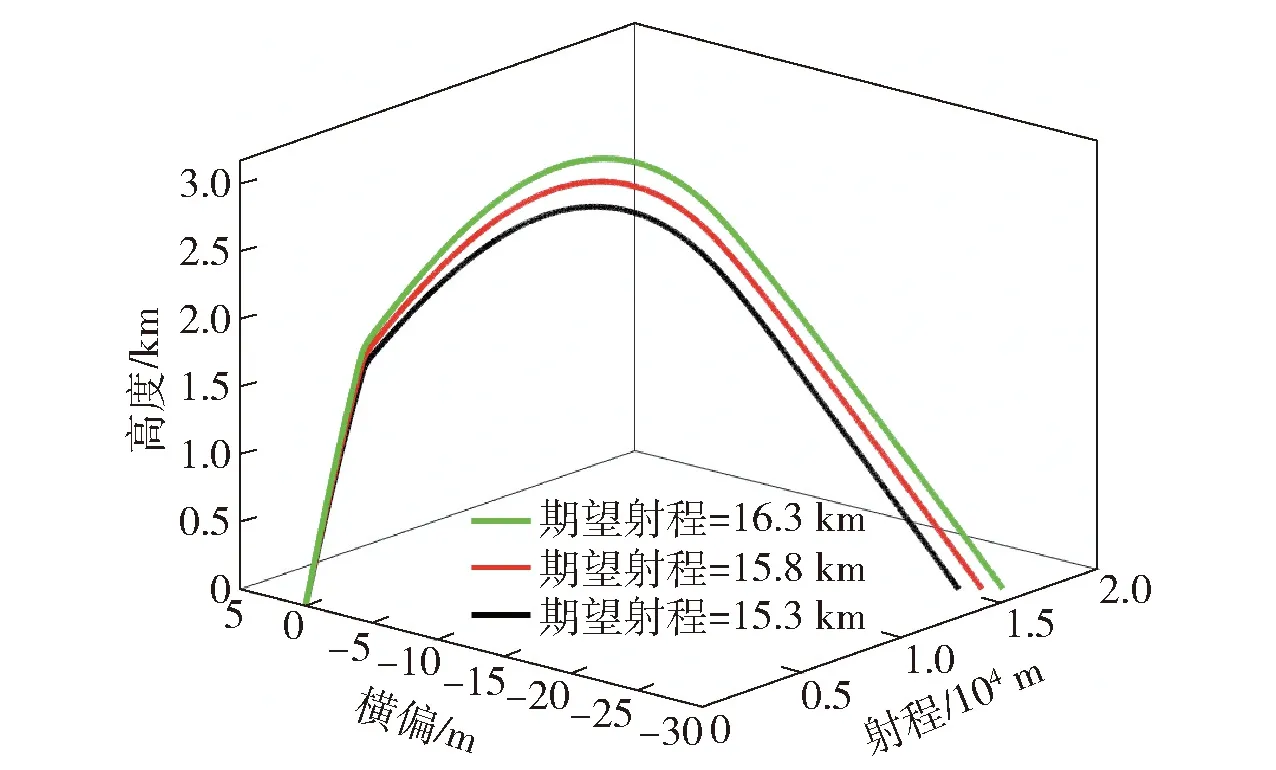
图11 多模型网络输出结果
由图11可以看出,多模型网络的输出射程、横偏与期望射程、横偏相近。
由表4、表5可知,修正后的射程误差值仍然在20 m附近,误差率约为0.15%,修正后的横偏误差值小于1 m,因此可证明本文设计的多模型网络精度较高。
3.3 蒙特卡洛实验
为进一步验证多模型网络的精度,进行蒙特卡洛仿真实验,初始条件与3.2节相同,选择第2组的实际气象,期望射程从[13 km,18 km]中随机选取。分别重复100次蒙特卡洛实验,绘制各次实验的射程误差,结果如图12所示。
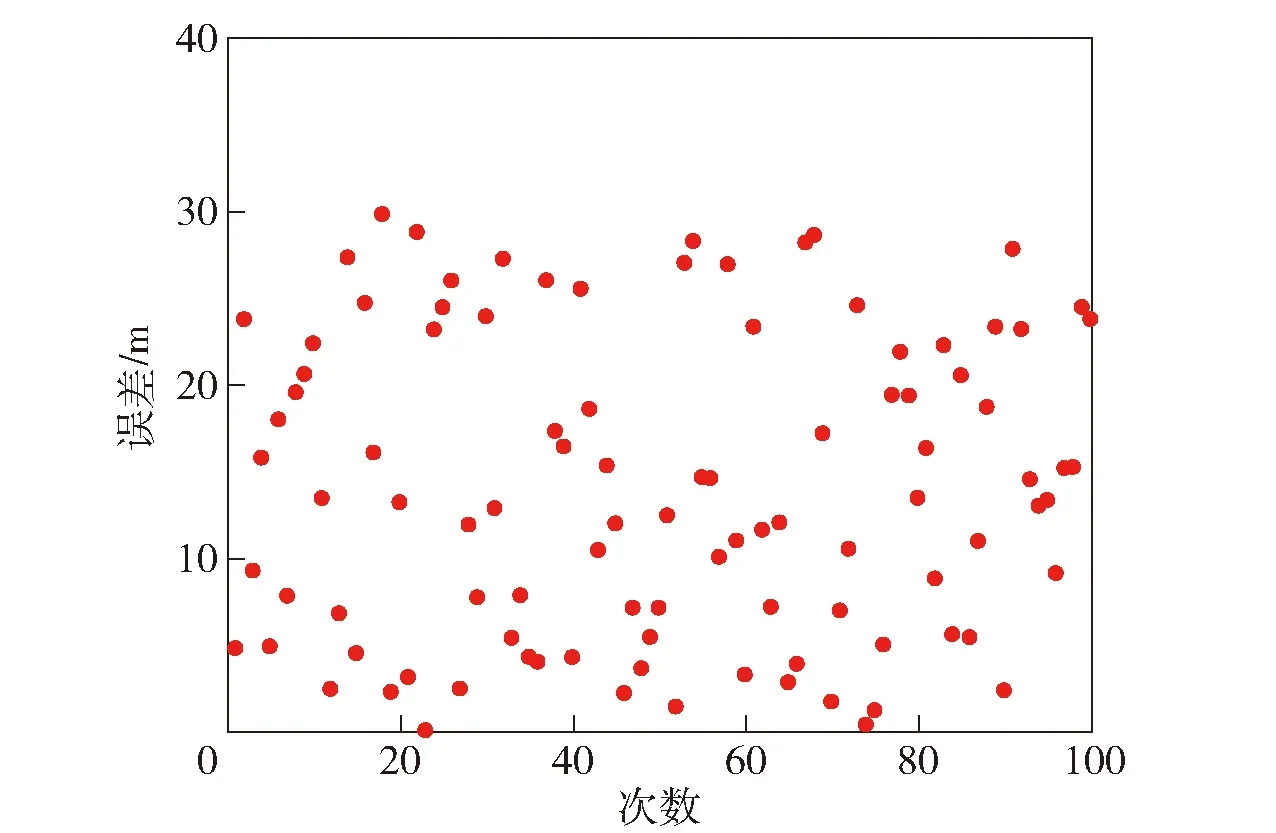
图12 蒙特卡洛仿真实验结果
由图12可知,误差最大值为29.6 m,方差为9 m,最大相对误差不到0.1%,本文设计的多模型网络误差较小,精度较高,可满足发射要求。100次 蒙特卡洛实验射表解算的平均时间为 46 ms,本文方法解算时间为34 ms。由此可见,本文方法不仅在精度上有一定的提升,同时也可实现快速解算。
3.4 仿真对比验证
为对比验证基于多模型网络与射表解算的精度,初始条件与3.2节相同,期望射程为15.3 km及16.3 km,二者关于诸元的求解结果如图13及表6所示。

表6 误差对比
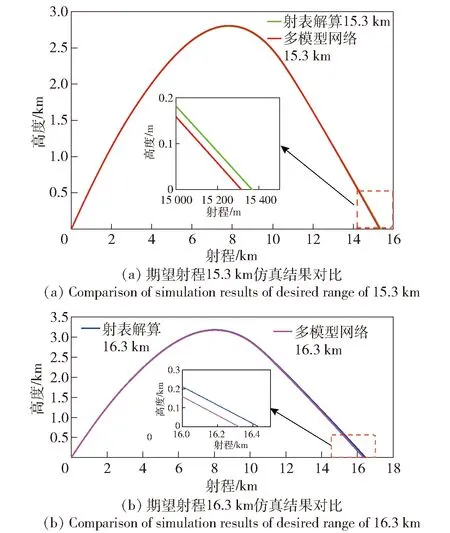
图13 仿真结果对比
由图13可知,相对于射表解算,多模型网络更接近期望射程,具体误差及精度如表6所示。
由表6可知,两组期望射程下多模型网络相对于射表解算精度更高,可提高100 m。在[13 km,18 km]射程范围内每间隔500 m做上述实验,多模型网络的误差方差为21.7 m,射表解算的误差方差为117.6 m。由此可见,基于多模型网络求取的诸元相对于射表解算精度更高。
3.5 实际飞行验证
为验证多模型网络在实际飞行实验中的精度,2022年7月,对多模型网络进行飞行试验论证。此次飞行试验期望射程为16.00 km,将实际气象输入到多模型网络中,网络得到的实际射击诸元如表7所示。

表7 实际射击诸元
根据上述诸元与射表解算进行理论仿真验证,误差如表8所示。
通过上述仿真验证可以看出,多模型网络相对于射表解算与期望射程更为接近。采用上述诸元进行的两次飞行试验均中靶,如图14所示。

图14 飞行试验效果
由图14可知,两次飞行均命中,验证了基于多模型网络的诸元解算方法的有效性。
4 结论
本文针对基于射表解算射击诸元精度差的问题,提出了一种基于多模型神经网络的诸元解算模型。首先建立了末制导炮弹6自由度弹道模型,利用数学仿真手段构建训练、测试及验证样本。其次分析了气象条件,对气温、气压进行拟合,对风引入层权求解。再次,对多模型网络中每个DNN的训练样本进行训练。得到主要结论如下:
1)训练完毕的多模型网络在不同期望射程下都表现出较高精度,在100次蒙特卡洛试验中误差较小。
2)通过仿真对比可知,多模型网络相对于射表解算出的诸元精度高,进一步证明了本文方法的优势。
3)在实际飞行试验中两次均中靶,验证了多模型网络在实际飞行试验中的有效性。本文提出方法通用性良好,可推广到各类精确制导武器。
