复杂环境下多无人机目标跟踪与避障联合航迹规划

2023-10-07赵军民何浩哲王少奇聂聪焦迎杰

兵工学报 2023年9期

赵军民, 何浩哲, 王少奇, 聂聪, 焦迎杰

(1.西北工业大学航天学院, 陕西西安 710072; 2.西安现代控制技术研究所, 陕西西安 710065)

0 引言

经过几十年的发展,无人机(UAV)技术日趋成熟,可以在复杂环境执行多样化任务[1-2]。在侦察监视、对抗打击、城市反恐和海上搜救等诸多任务场景中,UAV都需要对目标进行持续跟踪[3-5]。随着UAV间通信技术和协同控制技术的不断进步,采用多架UAV协同执行目标跟踪任务,可以增大对目标的观测面积,提高对目标状态的估计精度,提升对复杂环境的适应能力,因此受到广泛关注[6-8]。

对于固定翼UAV,在多个UAV协同执行目标跟踪任务时,常令它们按照一定的相位关系在目标上方具有指定半径的Standoff圆上进行盘旋跟踪,这种方式也称为Standoff跟踪。文献[9]针对多UAV对地面目标进行Standoff跟踪的航迹规划问题,设计了两个Lyapunov导引向量场(LGVF),控制各架UAV以期望相位关系收敛到目标上方的Standoff圆上,绕目标进行跟踪,这种方法只适用于无障碍物存在的理想环境。

UAV在低空执行任务时,常存在影响飞行的障碍物,且具有密集性、非凸性、动态性和不确定性[10],因此在多UAV进行目标跟踪时,需要进行避障航迹规划。人工势场(APF)法由于具有计算量小和航迹光滑等优点,已成为最常用的UAV避障航迹规划算法之一[11]。但是由于在APF法中没有障碍包络的设定,依赖调整力场生成航迹,当力场参数调整不当时UAV有可能进入障碍内部,导致避障失败[12]。在进行多UAV目标跟踪和避障联合航迹规划时,有学者提出了基于扰动流场的航迹规划方法[13-14],将目标跟踪速度作为初始汇流速度,通过修正汇流速度得到的扰动流场速度即可作为UAV速度指令。还有学者对目标跟踪与避障分别进行实时航迹规划,再将两种速度指令直接相加,得到UAV最终的速度指令[15]。然而,这种方法未考虑到避障任务事关UAV自身安全,比目标跟踪任务具有更高的优先性,将两种速度指令直接相加可能会减小UAV避障速度分量,导致在遇到密集型障碍物时UAV与障碍物距离过近,甚至进入障碍物内部出现避障失败的情况。

针对无人系统的多任务行为控制问题,Arrichiello等提出零空间方法来综合不同任务行为的控制指令[16]。零空间是指执行任务时不需要用到的维度空间,例如UAV在水平面内进行巡航飞行时,高度空间便是零空间。该方法强调将无人系统需要执行的任务进行划分,并确定优先级。通过将低优先级任务向高优先级任务零空间进行投影的方式来得到处理后的低优先级任务行为,然后与高优先级任务行为进行相加。这样可以保证高优先级任务行为不受低优先级任务行为的影响,同时部分执行低优先级任务行为[17]。

本文针对多个固定翼UAV在密集障碍环境中协同跟踪地面目标的任务场景,提出一种基于零空间方法的目标跟踪与避障联合航迹规划算法。首先,基于LGVF方法对多UAV进行Standoff跟踪实时航迹规划,得到使多个UAV能以期望相位关系收敛到Standoff圆上的速度指令,同时设计避障人工势场函数,进行UAV避障实时航迹规划,得到避障速度指令;然后,基于零空间方法进行目标跟踪与避障联合航迹规划,通过将目标跟踪速度指令向避障任务零空间投影后再与避障速度指令相加的方法得到UAV最终的速度指令。仿真结果表明,本文提出的联合航迹规划算法可使多UAV协同跟踪地面目标并有效避障,提升了UAV执行目标跟踪任务时的避障能力和安全性。

1 问题描述

多UAV对地面目标进行Standoff跟踪时,一般在基准高度的二维平面上飞行,UAV最大速度高于目标移动速度。

UAV的运动模型为

(1)

式中:[x,y]T为UAV在惯性坐标系下的水平位置;vu、φu和ωu分别为UAV速度、航向角以及偏航角速度。

同时,对于固定翼UAV,需考虑以下约束[18]:

(2)

式中:vmax和vmin分别表示UAV的最大速度和最小速度;ωmax表示UAV的最大偏航角速度。

Standoff跟踪的示意图如图1所示,其中Oxyz表示东北天坐标系,Otxtytzt表示以目标质心为原点、坐标轴方向与东北天坐标系相同的目标坐标系。UAV1、UAV2和UAV3共3架UAV均匀分布在Standoff圆上,对目标进行盘旋跟踪。

图1 多UAV Standoff跟踪示意图

多UAV在协同执行目标跟踪任务时需要进行机间通信,以获取机间相对运动信息和对目标的探测信息。多UAV的通信网络可通过通信拓扑图来描述。对单个地面目标进行跟踪时使用的UAV数量通常不多于4架(一般为2～4架)[19],因此本文采用全连通的无向图作为多UAV的通信拓扑,即任意两个UAV之间可以相互收发信息。

对于飞行环境中的障碍物,其外形往往是不规则的。但对于多UAV目标跟踪问题,可按规则外形包络处理,如圆形(二维空间中)[20]、球形或椭球形(三维空间中)[21]。本文UAV在二维平面飞行,因此可将障碍物视为圆形。记障碍物中心坐标为[xobs,yobs]T,半径为rmin,则UAV与障碍物中心的水平距离为

(3)

以障碍物中心作为避障人工势场的中心,设定人工势场的最大作用半径为rmax。图2为障碍物及避障人工势场的示意图,当robs≤rmax时,避障人工势场产生作用;当robs≤rmin时,UAV与障碍物发生碰撞。

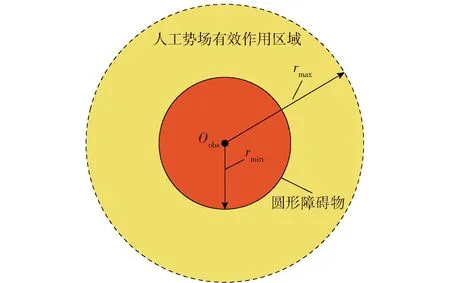
图2 障碍物及人工势场示意图

在多UAV协同跟踪地面运动目标时,一旦进入障碍物人工势场的有效作用区域,则UAV既需要进行目标跟踪航迹规划,还需要进行避障航迹规划。目标跟踪与避障联合航迹规划是指通过对UAV同时进行目标跟踪航迹规划和避障航迹规划得到速度指令,使UAV安全避开障碍物并持续跟踪目标。

2 目标跟踪与避障航迹规划

通过目标跟踪航迹规划和避障航迹规划分别得到UAV目标跟踪与避障的实时速度指令,是在复杂环境下进行联合航迹规划的基础。本节以LGVF方法作为多UAV目标跟踪的航迹规划算法,得到UAV跟踪目标的速度指令,并构建避障人工势场函数,利用APF方法进行UAV避障航迹规划,得到UAV的避障速度指令。

2.1 基于LGVF的目标跟踪航迹规划

(4)

为保证这N架UAV对目标的最佳观测配置,它们在Standoff圆上需要满足以下相位关系[22]:

(5)

式中:θij为两个相邻UAVi和UAVj在对峙圆上的相位差。其中,UAVi在对峙圆上的相位θi是指从目标指向UAVi的向量与Otxt轴正向的夹角,其大小从Otxt轴正向逆时针计起,范围为[0,2π)。θij的具体计算方法为

(6)

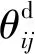
(7)

它们在Standoff圆上的相位关系如图3所示。

图3 UAV在Standoff圆上的相位关系

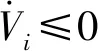
具体地,设UAVi(i=1,2,3)与目标的相对距离Lyapunov函数为

(8)

式中:R为Standoff圆半径。相位差Lyapunov函数为

(9)

(10)

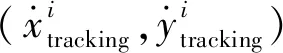
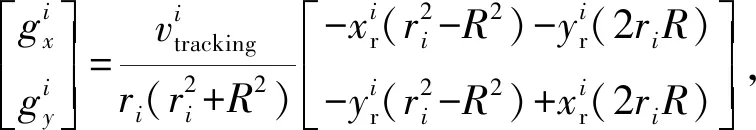
(11)

(12)

式中:v0为恒定的速度大小;k1和k3为相位系数。

为保证目标跟踪速度指令式(10)的大小与式(12)期望速度大小一致,应有

(13)

式(10)便是基于LGVF方法进行多UAV协同目标跟踪实时航迹规划得到的UAV速度指令,将式(11)、式(12)和式(13)代入式(10),便可以得到各UAV目标跟踪速度指令的具体值。

2.2 基于APF的避障航迹规划

APF方法的核心是设计合适的障碍物模型和人工势场函数[23]。在问题描述中障碍物模型的基础上,构建如下避障人工势场函数J(p)[24]:

(14)

式中:p=[x,y]T表示UAV水平位置;b0和c0为常数,分别决定人工势场的幅值和变化速度。

(15)

式中:r=[x-xobs,y-yobs]T表示UAV与障碍物的相对位置。

若环境中存在多个密集障碍物,则UAV同时处于多个障碍物人工势场的有效作用区域时,根据可加性原理,其受到的总虚拟排斥力为多个虚拟排斥力之和,即

(16)

式中:Ftotal(p)表示UAV受到的总虚拟排斥力;m表示对UAV产生虚拟斥力的障碍物总数。

以Ftotal(p)作为UAV的避障速度指令vavoidance,即

(17)

3 基于零空间方法的目标跟踪与避障联合航迹规划

针对多UAV协同目标跟踪与避障问题,将目标跟踪与避障作为UAV需要执行的不同任务。避障关乎UAV安全,因此与目标跟踪相比具有更高的任务优先级。本文目标跟踪与避障联合航迹规划方法是分别进行这两种航迹规划得到两个UAV速度指令,再基于零空间方法将这两个速度指令进行联合,得到UAV最终速度指令。

设避障任务函数为

(18)

式(18)对时间的导数为

(19)

式中:J1为避障任务函数Jacobi矩阵;vu为UAV速度矢量。

利用最小二乘法得到式(19)中vu的最小二乘解为

(20)

将式(19)代入上式,有

(21)

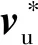
(22)

(23)

由式(23)可以看出,vNS不影响避障任务函数δ1,因此它是速度vu投影到避障任务零空间上的速度分量。

将式(21)代入vNS定义中,有

(24)

(25)

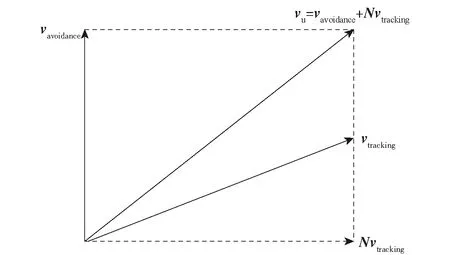
图4 基于零空间方法的联合航迹规划示意图

多UAV在障碍物存在的复杂环境中协同执行地面目标跟踪任务的航迹规划流程可总结为:如果UAV需要进行避障,则通过本文提出的联合航迹规划方法得到目标跟踪与避障联合速度指令;反之,则通过LGVF方法得到目标跟踪速度指令。各个UAV的航迹规划流程如图5所示。

图5 UAV航迹规划流程示意图

4 仿真验证

4.1 仿真条件

考虑一类典型任务场景:3架UAV组成编队在密集障碍物存在的环境中协同跟踪地面运动目标。设定UAV运动约束为vmax=21 m/s,vmin=19 m/s,ωmax=0.2 rad/s。3架UAV初始位置如表1所示,目标初始位置为(100 m,100 m)。Standoff圆半径R、UAV2速度大小常量v0、UAV1相位系数k1和UAV3相位系数k3,它们的具体取值如表2所示。分别对密集障碍环境中非机动目标和机动目标的跟踪任务进行仿真,以验证本文方法的合理性和有效性。

表1 UAV初始位置

表2 LGVF方法各参数取值

4.2 非机动目标跟踪任务的联合航迹规划仿真

设地面目标从初始位置以速度(10 m/s,0 m/s)做匀速直线运动,环境中存在3个障碍物,位置如表3 所示,它们具有相同的障碍物半径rmin=50 m和人工势场最大作用半径rmax=150 m。

表3 障碍物位置

在该任务场景中对本文提出的基于零空间方法的目标跟踪与避障联合航迹规划方法进行仿真。结果表明,3架UAV可以避开密集障碍物,在Standoff圆上协同跟踪非机动目标,如图6(a)～图6(e)所示。

图6 协同跟踪非机动运动目标的仿真结果

由图6(a)和图6(b)可以看出,3架UAV安全避开了3个密集障碍物。UAV1和UAV2在120 s左右收敛到Standoff圆上,UAV3在220 s左右收敛到Standoff圆上,如图6(c)所示。3架UAV在Standoff圆上的相位差在250 s左右振荡收敛到期望值,如图6(d)所示。3架UAV在收敛到期望相位过程中出现相位差振荡,是因为式(9)中相位差Lyapunov函数的导数并不能严格小于0。这是因为LGVF方法中得到的UAV目标跟踪期望速度大小即式(12)实际应为UAV相对于目标的期望速度大小,而真实的目标跟踪期望速度大小应为该速度大小与目标速度大小之和。但由于UAV存在最大速度约束,LGVF方法采取式(12)作为UAV期望速度大小。图6(e)表明3架UAV之间的距离始终在安全范围内,能够避免发生碰撞。

4.3 机动目标跟踪任务的联合航迹规划仿真

为验证本文方法在机动目标跟踪任务场景中的效果,考虑地面目标运动过程存在机动运动,具体如表4所示。环境中存在8个障碍物,前3个障碍物的位置和参数与4.2节相同,其余5个障碍物的位置和参数如表5所示。

表4 机动目标运动过程

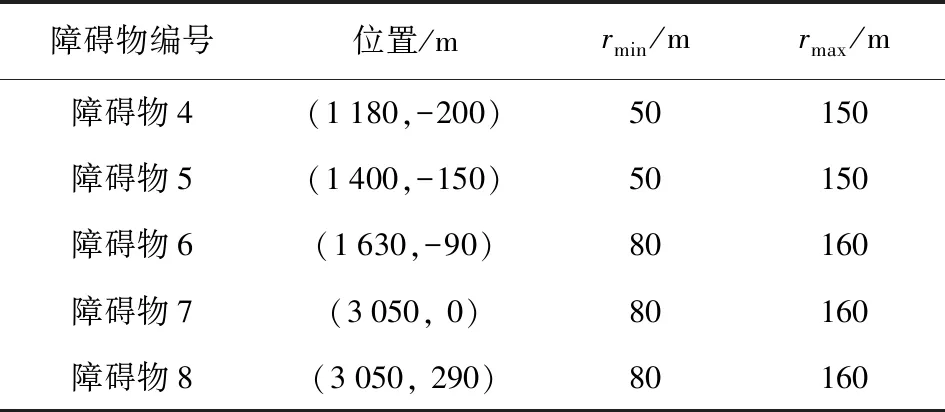
表5 障碍物位置和参数

仿真结果表明,3架UAV可以避开密集障碍物,在Standoff圆上协同跟踪机动目标,如图7(a)～图7(d)所示。

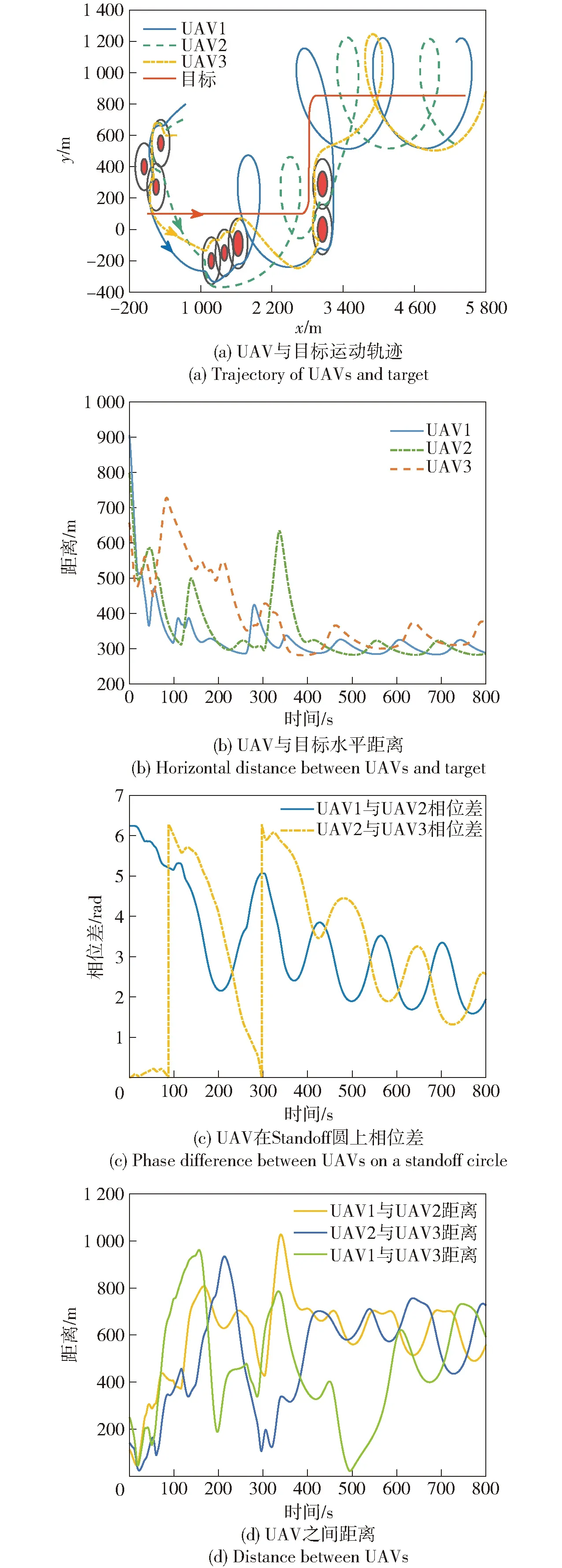
图7 协同跟踪机动运动目标的仿真结果

由图7(a)可以看出,整个仿真过程中目标运动形式改变,3架UAV始终可以有效避开障碍物,持续跟踪目标。由于避障时UAV速度指令不等于LGVF产生的目标跟踪速度指令,图7(b)中3架UAV与目标水平距离在UAV需要避障时出现波动,在避障完成后收敛到期望值。最终UAV1、UAV2和UAV3分别在335 s、360 s和400 s收敛到Standoff圆上。图7(c)中UAV在Standoff圆上相位差在收敛到期望值过程中出现波动,同样是由UAV进行避障引起的。避障完成后,UAV相位差振荡收敛到期望值附近。由图7(d)可以看出,3架UAV之间的距离始终都在安全范围内,避免了机间碰撞。

4.4 障碍物半径rmin和APF最大作用半径rmax对算法性能的影响

在4.3节仿真条件基础上,设障碍物7和障碍物8的半径依次同时增大到100 m和150 m,其余参数不变。仿真得到不同障碍物半径下3架UAV与障碍物7中心和障碍物8中心的最小距离分别如表6 和表7所示。

表6 不同rmin下各UAV与障碍物7中心的最小距离

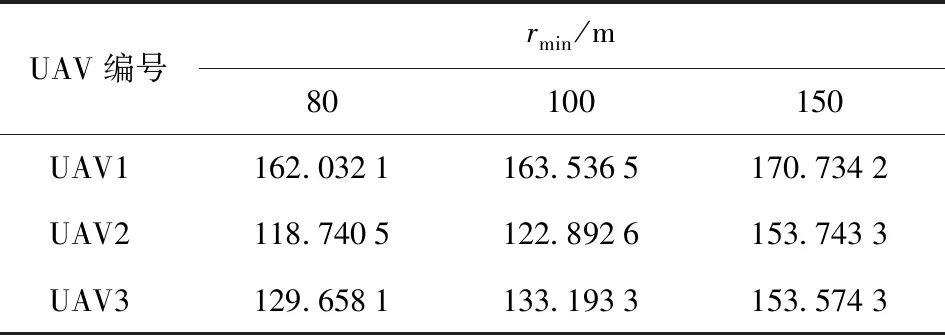
表7 不同rmin下各UAV与障碍物8中心的最小距离

由表6和表7可以看出,在不同的障碍物半径下,3架UAV与2个障碍物中心的距离都大于障碍物半径,表明UAV可以避开障碍物对目标进行持续跟踪。随着rmin的增大,3架UAV与障碍物中心的距离也依次增大。这是因为APF的最大作用半径rmax相同时,由式(15)可知,在APF作用范围内的相同位置,rmin增大引起UAV避障速度增大,即UAV在障碍物法向方向的速度增大。

考虑UAV与障碍物边缘的距离等于UAV与障碍物中心的距离减去障碍物半径。由表6和表7可以看出,随着rmin的增大,UAV与障碍物边缘的距离减小,当rmin=150 m时该距离最小为2.04 m,UAV安全风险增大。这是因为rmin增大而rmax保持不变,在进入APF作用范围后,UAV与障碍物中心距离的增幅小于rmin的增幅。因此,当障碍物半径增大时,应增大APF最大作用半径,使UAV在距离障碍物边缘更远的位置开始避障。

下面进一步分析rmax对算法性能的影响。在4.3节仿真条件基础上,设障碍物7和障碍物8的半径保持80 m不变,依次同时增大其rmax到220 m和300 m,其余参数不变。仿真得到不同rmax下3架UAV与障碍物7中心和障碍物8中心的最小距离分别如表8和表9所示,UAV在Standoff圆上的相位差如图8所示。

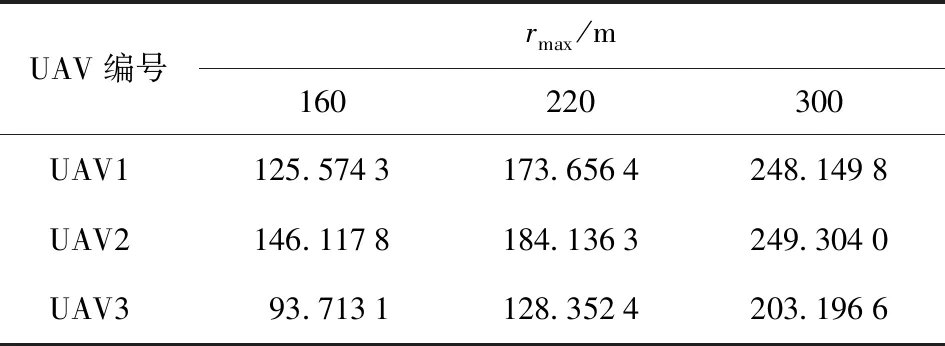
表8 不同rmax下各UAV与障碍物7中心的最小距离

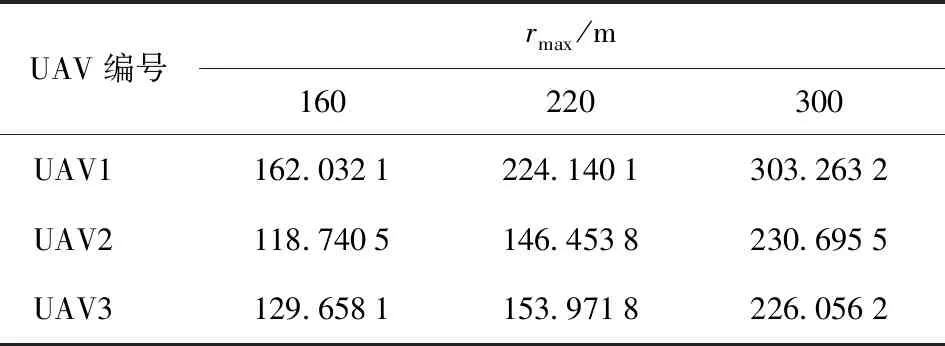
表9 不同rmax下各UAV与障碍物8中心的最小距离

图8 不同rmax下UAV在Standoff圆上相位差

由表8和表9可以看出,rmax取不同值时,UAV与障碍物中心的距离始终大于障碍物半径,UAV可以避障。增大rmax,APF作用范围变大,UAV会在更大区域范围内产生避障速度,UAV与障碍物中心的距离也随之增大。由于障碍物半径保持不变,UAV与障碍物边缘的距离也随之增大,UAV避障性能提升。由图8可以看出,rmax取值160 m和220 m时,在避障过程中UAV相位差波动相对较小,而rmax取值300 m时,UAV相位差波动变大,目标跟踪性能受到影响。这同样是因为APF作用范围变大,UAV避障过程变长,UAV需要在更大区域范围内按照零空间方法得到的速度指令飞行,而不能按照目标跟踪速度指令飞行。因此,在rmin已知时,选取rmax需要综合考虑UAV避障性能和目标跟踪性能,根据经验,rmax取值一般是rmin的2～3倍。

4.5 仿真对比

为进一步说明本文基于零空间的目标跟踪与避障联合航迹规划方法的优势,将本文方法与已有的两种方法进行对比。这两种方法是将速度指令直接相加的联合航迹规划方法和基于扰动流场的联合航迹规划方法,下文分别简称为直接相加方法和扰动流场方法。在4.2节仿真条件下对这两种方法进行仿真,直接相加方法和扰动流场方法的仿真结果分别如图9和图10所示。同时,计算整个仿真过程中本文方法和以上两种方法下各UAV与障碍物中心的最小距离,结果如表10所示。

表10 3种方法下各UAV与障碍物中心的最小距离

图9 直接相加方法仿真结果

图10 扰动流场方法仿真结果

由图9和图10可以看出,直接相加方法和扰动流场方法均可以使多UAV绕开障碍物,对目标进行持续跟踪。但是将图6(d)、图9(d)和图10(d)进行对比可发现,在UAV收敛到期望相位位置的过程中,本文方法下UAV之间实际相位差在期望相位差附近的振荡程度小于扰动流场方法下的振荡程度,并与直接相加方法下的振荡程度一致。这是因为本文方法和直接相加方法都是通过式(12)得到UAV目标跟踪期望速度大小,而扰动流场方法则是通过扰动矩阵乘以式(12)得到期望速度大小。因此与本文方法相比,扰动流场方法下UAV目标跟踪期望速度相对较小,导致其相位差Lyapunov函数的导数相对较大,具有更大的相位差振荡程度。同时,由表10 可以看出,本文方法下3架UAV与障碍物的最小距离均大于直接相加方法下的距离,且略小于扰动流场方法下的距离。这是因为本文方法和扰动流场方法增大了UAV在障碍物法向方向上的速度分量,因此避障效果更好。

综合以上分析可发现,扰动流场方法增大了UAV与障碍物的距离,同时也使UAV相位差振荡程度变大,多UAV实际相位分布与期望分布差距较大;直接相加方法避障性能较差,但是具有相对较小的相位差振荡程度。本文方法兼顾了UAV目标跟踪相位协同分布和避障性能,在增大UAV与障碍物距离时依然能保证UAV在Standoff圆上的相位差具有较小振荡。因此,综合比较多UAV目标跟踪协同效果和避障效果,本文所提方法具有最优性能。