基于贪心遗传算法的液晶光学相控阵多光束扫描

叶闻语, 王春阳*, 于金阳, 拓明侃, 王子硕

(1.西安工业大学 西安市主动光电成像探测技术重点实验室, 陕西 西安 710021;2.长春理工大学 电子信息工程学院, 吉林 长春 130022)

0 引言

液晶光学相控阵是一种非机械式光束扫描控制器件,具有体积小、耗电量低、灵活性高、电控可编程、稳定性好等优点[1-5],在激光雷达、空间光通信、光学成像和自适应光学等领域具有广泛的应用前景[6-9]。目标捕获效率是激光相控阵雷达的一项重要指标[10],在对动态目标进行扫描时,不同的扫描方法捕获效率也不相同。目前液晶光学相控阵激光的扫描方法均为单光束扫描,主要分为以下4种:逐行扫描、蛇形扫描、螺旋扫描、高斯扫描[11-12]。这4种扫描方法对扫描区域内所有位置进行全部扫描,扫描周期较长,成像速率不高;在针对目标信息未知的情况下有着良好的目标搜索功能,但对于已知信息的目标,其捕获效率不高。

近些年一些学者提出了利用液晶光学相控阵生成多光束并进行扫描的方案。汪相如等提出了液晶光学相控阵的双波束成形及二维扫描方法[13],实现了两个光束的单个角度偏转。Golmohammagy等提出了部分锁相相干平顶激光束阵列[14],实现了4个圆形阵列光束的生成。王承邈利用光束分束系统与液晶光栅组合,实现了多光束并行扫描[15]。但这3种扫描方法均不能实现多个光束在二维方向上的独立扫描,无法针对多个目标进行独立的扫描,对目标的捕获效率较低。

因此,本文使用多个液晶光学相控阵设计了多光束生成的方案,以实现多个光束在同一扫描区域内、二维方向上的独立扫描;提出基于贪心遗传算法的多光束扫描方法,确定多个动态目标的扫描顺序,能够有效缩短扫描周期,提高目标的捕获效率。选取目标捕获效率作为算法的目标函数;根据目标的已知信息,利用贪心算法生成初始扫描序列,对多光束扫描序列采用整数编码以提高算法搜索速度,使用轮盘赌的方式选择扫描序列,经过多代的遗传和变异后,得到目标捕获效率最大的多光束扫描方法。

1 液晶光学相控阵多光束扫描机理

1.1 液晶偏振光栅偏转机理

本文采用液晶光学相控阵器件为液晶偏振光栅(LCPG),LCPG是由具有介电各向异性和光学各向异性的向列相液晶,玻璃基板,光取向层构成[9],液晶分子取向沿着玻璃基板平面呈周期性规律排布[16],其基本结构如图1所示。图1中,Λ为光栅周期,取0、±1。

图1 液晶偏振光栅基本结构

通过式(1)光栅方程[17]可求出光束入射到液晶偏振光栅之后的偏转角度θo,

(1)

式中:λ为入射光束波长;o为衍射级次;θi为入射光角度。

当光束发生0级衍射时光束不发生偏转;当光束发生1级衍射时光束偏转方向与入射光的旋性有关,入射光为右旋圆偏光时光束向上偏转,入射光为左旋圆偏光时光束向下偏转[18]。光束通过加电的电控波片(LCHWP)后,光的旋性会发生改变。因此,将LCHWP与LCPG组合,可以实现光束在0级、±1级三个衍射级次之间的切换,光束偏转如图2所示,其中V表示给LCHWP施加的电压。

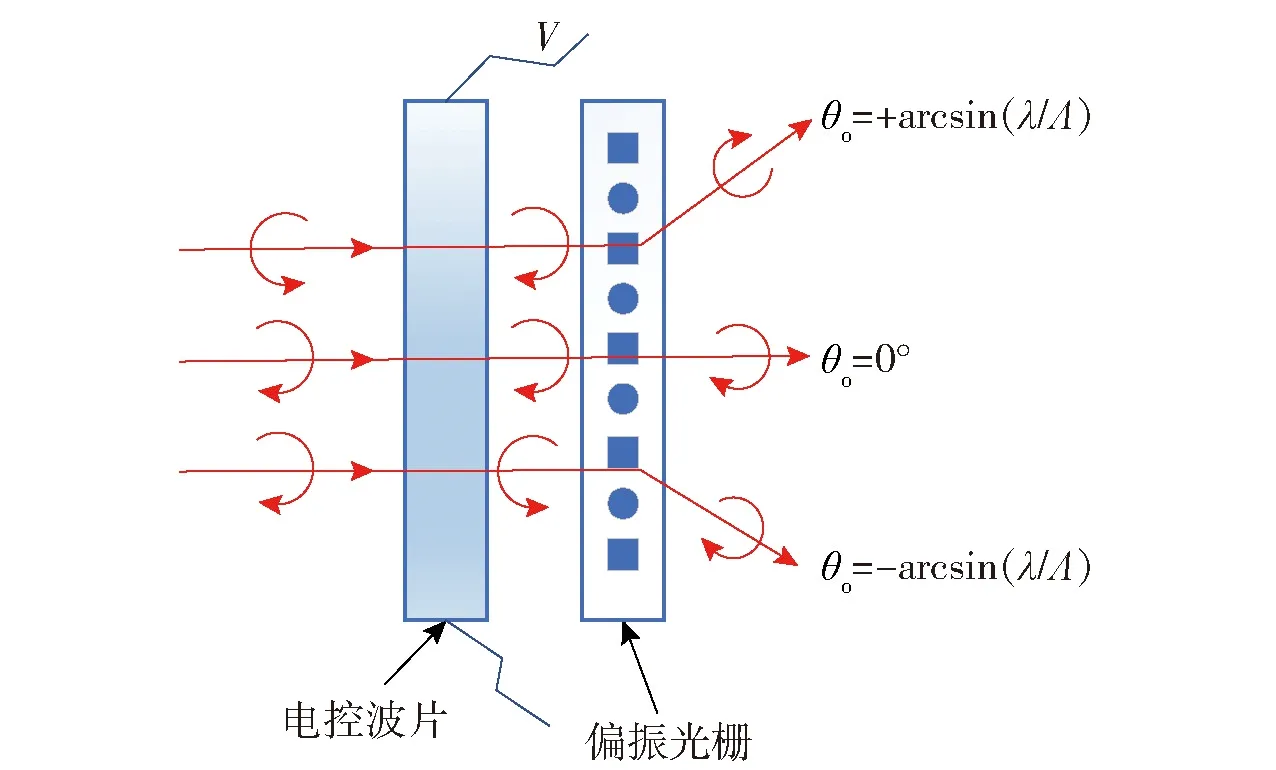
图2 光束偏转示意图

1.2 液晶偏振光栅的级联

单个LCHWP与LCPG组合只能偏转有限角度,而且偏转角度较小。通过多片LCHWP与LCPG级联可以实现多角度的大范围光束偏转[19]。本文采用二进制级联的方式,将8片LCHWP与4片y轴方向LCPG、4片x轴方向LCPG组合,结构如图3所示。

图3 LCHWP与LCPG组合结构

二进制级联方式[20]在x轴方向和y轴方向上,能实现的总偏转角个数R、最大光束偏转角度θm与LCPG个数Q的关系表达式为

R=2Q+1-1

(2)

θm=δ(2Q-1)

(3)

式中:δ为角度分辨率,即第1片的衍射角度0.33°。因此该系统在x轴方向和y轴方向上,分别可实现最大偏转角度为±5°的光束偏转,且角度分辨率为0.33°,能实现31个偏转角度[9]。

1.3 液晶光学相控阵多光束形成及扫描

本文系统基于液晶光学相控阵原理和晶体光学理论,将激光器、分光棱镜、反射镜、1/4波片、液晶相控阵1、液晶光学相控阵2共7个主要组件,按照图4所示搭建光路。

激光经过分光棱镜后,生成两束垂直的光束;其中一个光束传播方向保持不变,经过1/4波片后由线偏振光转换为圆偏振光,入射到液晶光学相控阵1中;另一个光束垂直于原光路方向传播,通过反射镜调整其传播方向,再经过1/4波片入射到液晶光学相控阵2中。对两个液晶光学相控阵施加不同的电压,即可实现两个光束在同一扫描区域上的二维扫描。

由于本文系统最大偏转角度为±5°,在x轴方向和y轴方向均选取0.67°为角度分辨率,则在光屏上可预设16×16个扫描光斑(见图5)。图5中,r为扫描光斑半径,Δd为预设光斑间的距离。

图5 16×16扫描光斑

利用两个光束对扫描区域按照传统扫描方法进行扫描,扫描路径如图6所示。

2 基于贪心遗传算法的多光束扫描方法

假设给定M个光束、N个目标,每个目标n(n=1,2,…,N)的初始信息为

En={xn,yn,Sn,vn}

(4)

式中:xn和yn分别表示目标n相对于扫描区域原点的位置;Sn表示目标n的面积;vn表示目标n的速度。

设目标扫描周期T,则每个光束m(m=1,2,…,M)扫描目标消耗的时间不能大于目标扫描周期T:

(5)

式中:tmn为光束m跟踪目标n的时间;Cmn表示光束m是否跟踪目标n,

(6)

既每个目标在T周期内只被扫描一次。

在T时间内M个光束对N个目标扫描的捕获效率记为P,为了在时间T有限情况下提高目标的捕获效率,即在较短时间内捕获到更多的目标,目标函数设为目标捕获效率之和P最大化[21]:

(7)

针对上述多光束扫描模型中目标函数的求解问题,贪心算法可以在较短时间内找到一个较满意的解[22],但所得出的解存在局部最优的问题。遗传算法能获得全局最优解,但算法的收敛性能不好,不能在较短的时间内找到最优解。因此,本文采用贪心遗传算法进行求解,先用贪心算法生成一个初始的扫描序列,然后通过遗传算法进行选择、交叉和变异操作,使得扫描序列对应的目标捕获效率增加,从而输出最优扫描序列。

2.1 贪心算法产生初始种群

传统的遗传算法中初始种群完全随机产生,算法搜索周期较长[23]。贪心遗传算法是由贪心算法产生的近似最优解X1,作为初始种群中第1个个体,可有效缩短算法迭代周期,X1对应的扫描周期T作为目标扫描周期;用随机方法产生其他个体,形成初始种群X=(X1,X2,…,Xsize),size为种群规模。

本文算法最终求得的最优扫描序列,除了需要保证目标捕获效率最大,还需要保证扫描周期较短,因此将目标扫描周期T作为约束条件。在初始种群中,其余扫描序列Xz(z=2,…,size)都是随机产生的。部分Xz对应的扫描周期可能会大于目标扫描周期,即使该扫描序列对应的捕获效率较高,也无法成为该算法的最优解,此扫描序列被称为不可行解。为了进一步提高算法的搜索效率,需要先对此不可行解Xz进行修复操作。

2.2 编码

对于扫描序列的编码方式采用整数编码。整数编码方式具有更小的搜索空间复杂度,因此具有更快的收敛速度[23]。

M个光束、N个目标的扫描序列,经编码后可表示为Xz=(x1,x2,…,XN+M-1)(xi=0,1,…,N),其中,0表示不同光束扫描序列之间的间隔点。例如2个光束对7个目标扫描可以表示为如下8位整数制串(3,1,4,7,0,2,5,6),该编码表示目标1、3、4和7由光束1进行扫描,扫描顺序为3-1-4-7,目标2、5和6由光束2进行扫描,扫描顺序为2-5-6。

2.3 适应度函数

在进行个体适应度评价时,使用目标捕获效率P作为适应度函数。目标捕获效率P的计算方式如下。

在使用双光束进行二维扫描时,扫描区域内的光斑位置是固定的。以目标匀速运动模型为例,为了有效地计算对动态目标扫描的捕获效率,根据扫描区域内预设的I×J个扫描位置,按照设定的扫描路径进行扫描[24],在不考虑扫描延时的情况下,扫描间隔记为TS,可得到光斑脉冲的时间矩阵t:

(8)

矩阵中的tij是指光斑出现在第i行第j列位置的时间,不同的扫描方法所对应的时间序列矩阵不同。

根据t可以确定在tij时刻的光斑中心位置(x0,y0),对于目标区域Sn,将目标区域分为L×W个点,每个点的面积为Spt=Sn/(L×W),并计算出每个点对应的位置坐标(xlw,ylw),以及每个点在tij时刻到光斑中心(x0,y0)的距离dlw为

(9)

每个点在tij的下一时刻对应的位置(xij,yij),以及到(x0,y0)的距离d′lw为

(10)

当dlw≤r&&d′lw≤r时捕获点数增加一次,求得捕获点次数nt,扫描完成后捕获点面积Snt为

Snt=Spt×nt=Sn×nt/(L×W)

(11)

捕获点面积Snt与所有光束扫描面积的比值,既在tij时间段内光束m对于目标n扫描的捕获效率Pmn(t):

(12)

则在T时间内M个光束对N个目标扫描的捕获效率P为

(13)

2.4 修复

在随机产生初始解和遗传操作(交叉和变异算子)过程中,产生的一些不可行解Xz采用如下方法进行修复:

步骤1将超过目标扫描周期T约束的目标扫描序列,按照目标所需的扫描时间tn升序排列。

步骤2按上述排列的先后次序,依次将目标分配给扫描周期最短的光束,直到形成可行解为止。

步骤3如果无法生成可行解,则在种群中剔除此不可行解。

2.5 选择算子

选择算子是挑选父代种群中的个体,并确定该个体被挑选的可能性[23]。

本文采用轮盘赌[25]的方法:先计算出种群中每一个扫描序列所对应的适应度值,即该扫描序列对应的目标捕获概率P(Xz),再计算出此适应度值在群体适应度值中所占的比例,即为此扫描序列遗传到下一代中的概率F(Xz),

(14)

在选择个体时需要进行多轮选择,每一轮产生一个[0,1]均匀随机数,根据F(Xz)是否大于该随机数来确定是否选择个体Xz并采用精英法则,强行将上一代的最优个体直接进入下一代[25],可以保证下一代的最优个体一定不劣于上一代。

2.6 交叉与变异

1)单点交叉操作。可以有效地保持群体的稳定性,避免产生过多的不可行解。单点交叉操作方法是:随机产生两个交叉的点位,使父体(原始扫描序列)中两个点位的数据(即待扫描的目标)交换,形成新个体(新的扫描顺序)。

2)变异操作。采用变异可以有效地保持群体的多样性,使算法具有较强的搜索能力。 变异操作方法如下:随机地在父体中选取一个光束的扫描目标,将该目标放置在该父体中其他光束扫描顺序内,形成一个新个体。

2.7 算法步骤

基于贪心遗传算法的多光束扫描流程如图7所示。

具体步骤如下:

步骤1确定扫描参数。确定需要扫描的目标数量N,光束数量M,初始种群的规模size,遗传代数G。

步骤2贪心算法产生初始种群。采用整数编码方式,利用贪心算法产生X1,其余的初始种群随机产生,并对初始种群进行修复。

步骤3适应度值计算。通过式(8)～式(14),计算出初始种群中每个扫描序列的适应度值,即目标捕获效率。

步骤4扫描序列选择。采用轮盘赌的选择策略和精英法则,得到遗传到下一代中的扫描序列。

步骤5交叉以及修复。对于每一个扫描序列,产生一个(0,1)的随机数;当随机数小于交叉概率Pc时,随机选取该序列中两个目标进行交换,得到新的序列,并对新的扫描序列进行修复。

步骤6变异以及修复。对于每一个个体,随机选取产生一个(0,1)的随机数。当随机数小于变异概率Pm时,随机选取该序列中任一光束扫描的任一目标,并将该目标放置在该序列中其他光束的扫描序列中,并对新的扫描序列进行修复。

步骤7若达到迭代次数上限,则输出最优扫描序列,算法结束;否则转步骤4。

3 算法验证

3.1 仿真验证

本文采用2个光束,对传统扫描方法以及贪心遗传算法扫描方法进行捕获效率的对比。两个光斑中心之间距离为10 mm,光斑半径设为5 mm。目标以10 mm/s的速率沿直线匀速运动,光斑扫描间隔时间为0.02 s。图8为7个目标的仿真场景,其中N1～N7为目标。

图8 仿真场景设置

为了分析不同的目标数量对捕获效率的影响,分别采用4个目标(N4,N5,N6,N7)、6个目标(N1,N2,N3,N5,N6,N7)、7个目标(N1～N7)。图9为贪心遗传算法多光束扫描方法与3种多光束传统扫描方法的捕获效率P对比。

图9 目标数量不同时的扫描捕获效率

由图9可知,目标个数越多,捕获效率越高。当目标数量从4变化为7时,传统扫描方法的捕获效率由15%提高至25%,贪心遗传多光束扫描方法的目标捕获效率由75%提高至了83%,与传统扫描方法相比较,贪心遗传多光束扫描方法的捕获效率提高了3倍,并极大地缩短了扫描时间。

贪心遗传算法属于启发式算法,不能穷举所有的可行解,可能会陷入局部最优。较高的交叉概率可以使种群有较快的更新速度,提高搜索效率,但同时也会使高适应度的个体容易被淹没,算法陷入局部最优;变异机制避免算法陷入局部最优,变异概率越大,算法跳出局部最优的概率就越大,但较大的变异概率会导致算法不稳定。在利用贪心遗传算法针对7个目标求解最优多光束扫描序列时,本文设置了较高的交叉概率0.9以及变异概率0.1,算法可以快速得到局部最优解,但无法达到全局最优。增加遗传代数能够提高算法求得全局最优解的概率,同时保证算法的稳定性,但也增加了算法的计算量,降低了搜索效率。

为了验证算法的稳定性,设置遗传代数为100,进行20次重复实验,迭代结果如表1所示,其中1次的迭代曲线如图10所示。由表1中数据可知:遗传代数为100时算法基本上可以找到最优解,即最大捕获效率0.834 4;遗传至30代时,算法已基本可以达到近似最优解,20次迭代过程中,捕获效率的平均值已达到0.833 4,与最大捕获效率偏差为0.001,证明该算法已具有较高的稳定性。因此为保证算法的快速搜索能力以及稳定性,本文设置遗传代数为30。

表1 20次重复实验中贪心遗传算法迭代的最大捕获效率以及对应的遗传代数(遗传代数为100)

图10 贪心遗传算法迭代曲线

当光斑半径r以及目标速度v发生变化时,捕获点面积Snt也会发生变化,捕获效率P也会随之发生改变。图11为使用2个光束对7个目标进行扫描,当目标速度v保持10 mm/s不变而光斑半径r变化时,不同扫描方法捕获效率的对比。

图11 不同光斑半径时的扫描捕获效率

由图9(c)与图11(a)、图11(b)对比可知,随着扫描半径的增加,捕获效率逐渐增加。当光斑半径由4.5 mm增加至5.5 mm时,传统扫描方法的捕获效率由20%提高至30%,贪心遗传多光束扫描方法的捕获效率由70%提高至了95%。与传统的扫描方法相比较,贪心遗传多光束扫描方法的捕获效率提高了200%,扫描时间由2.5 s缩短为1 s。

当光斑半径r保持5 mm不变、目标速度v变化时,仿真结果如图12所示。

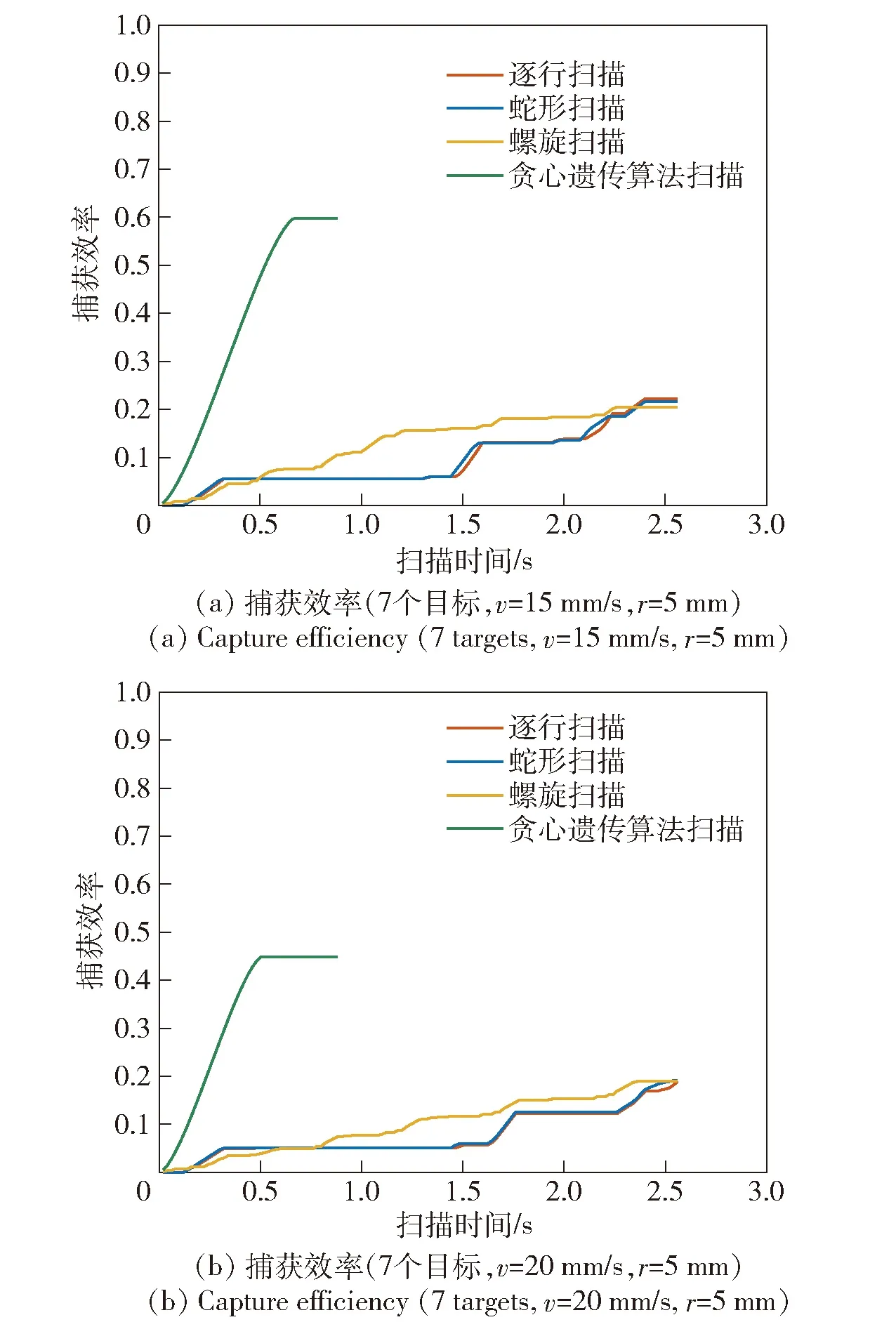
图12 不同目标移动速度时的扫描捕获效率

由图9(c)与图12(a)、图12(b)对比可知,随着目标速度的增加,捕获效率降低。当目标速度由10 mm/s增加至20 mm/s,传统扫描方法的捕获效率由28%降低至了18%,贪心遗传多光束扫描方法的捕获效率由95%降低至了45%。与传统的扫描方法相比较,贪心遗传多光束扫描方法的捕获效率提高了150%,扫描时间由2.5 s缩短为1 s。

综上所述,无论目标多少,光斑半径r以及目标速度v如何变化,与传统的扫描方法相比,基于贪心遗传算法的多光束扫描方法都能加快扫描速率,提高捕获效率。

3.2 实验验证

本文搭建了图13所示多光束扫描系统对所提优化方法进行实验验证,并与传统的扫描方法进行对比分析。

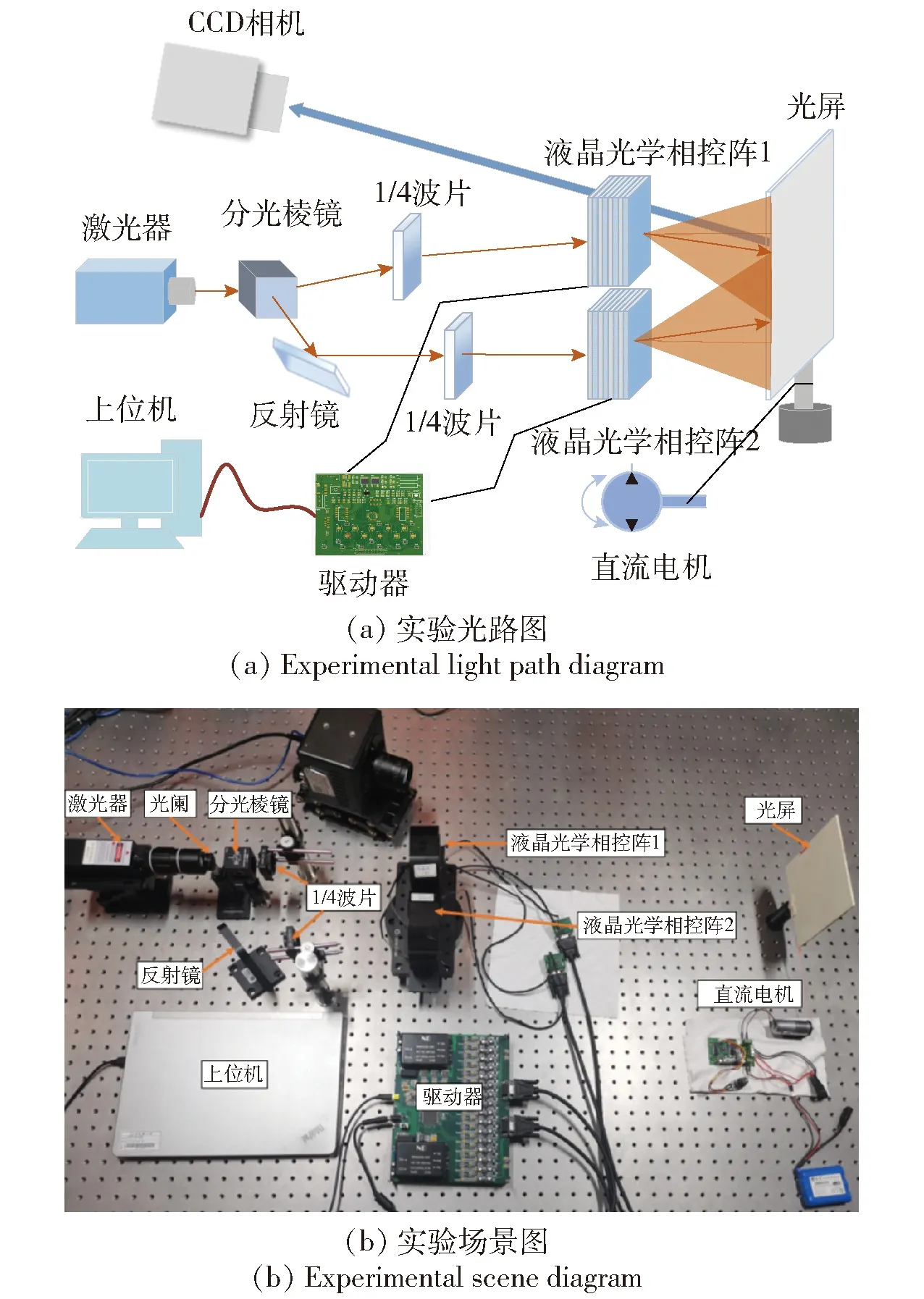
图13 多光束扫描系统实验

图13(a)为系统原理图,图13(b)为系统实验装置图,系统包括上位机、驱动器、1 064 nm激光器、光阑、分光棱镜、反射镜、1/4波片、两个液晶光学相控阵、光屏、CCD相机(日本滨松公司产)、光屏和直流电机。

实验中,扫描区域采用吸光布布置,7个目标由反光纸代替,位置和大小按照仿真实验等比例设置,如图14(a)所示。

图14 扫描目标与光斑显示

调节实验光路,使得光斑半径为5 mm,两个光斑之间距离为10 mm,扫描时间间隔为0.02 s。使用不同的扫描方法进行扫描,并利用CCD高速相机采集照片。当光斑照在吸光布上时,CCD相机中不显示光斑;当光斑扫描至反光纸上时,采集到的光斑如图14(b)所示。扫描一帧完成后,根据采集到的光斑面积与所有光束扫描面积的比值,即捕获效率P。

选用不同的目标数量N(N=4,6,7),根据采集到的光斑面积,计算出不同扫描方法的实际捕获效率如图15所示。

由图15可知,当目标数量从4变化为7个,传统扫描方法的实际捕获效率由20%提高至了35%,多光束扫描方法的实际捕获效率由40%提高至了50%。与传统的扫描方法相比,多光束扫描方法的捕获效率提高了约100%。

利用光阑调整光斑的半径,当目标速度保持10 mm/s的速度不变、光斑半径r变化时,实际捕获效率如图16所示。

图16 不同光斑半径时的实际捕获效率

对比图15(c)与图16(a)、图16(b)可知,随着扫描半径的增加,捕获效率逐渐增加。当光斑半径由4.5 mm增加至5.5 mm,传统扫描方法捕获效率由22%提高至40%,多光束扫描方法的捕获效率由42%提高至了70%。与传统的扫描方法相比较,多光束扫描方法的捕获效率提高了约75%,扫描时间由2.5 s缩短为1 s。

利用电机改变光屏的移动速度,即目标速度发生了改变,当光斑半径r保持5 mm不变,目标速度v变化时,实际捕获效率如图17所示。

图17 不同目标移动速度时的扫描捕获效率

由图15(c)与图17(a)、图17(b)对比可知,随着目标速度的提高,捕获效率降低。当目标速度由10 mm/s提高至20 mm/s时,传统扫描方法的实际捕获效率由28%降低至了15%,贪心遗传多光束扫描方法的实际捕获效率由62%降低至了38%。与传统的扫描方法相比较,贪心遗传多光束扫描方法的捕获效率整体提高了约150%,扫描时间由2.5 s缩短为1 s。

3.3 仿真与实验结果分析

对比分析图9和图15、图11和图16以及图12和图17,发现虽然受到了实验环境以及测量误差等因素干扰,但是实验结果与仿真结果基本一致。贪心遗传多光束扫描方法与传统扫描方法相比,在不同的目标数量情况下,捕获效率仿真结果提高了3倍,实验结果提高了100%;在不同的光斑半径下,捕获效率仿真结果提高了200%,实验结果提高了75%;在不同的目标速度下,捕获效率仿真结果提高了150%,实验结果提高了150%,并且在各种情况下都有效地缩短了扫描周期。

4 结论

本文提出了一种基于贪心遗传算法的液晶光学相控阵多光束扫描方法,在多个光束对多个动态目标进行扫描时,使用目标捕获效率作为目标函数,利用贪心遗传算法求解,确定各个光束的最优扫描顺序。得到主要结论如下:

1)本文算法利用贪心算法得到初始种群,增强了算法的搜索导向;设置了较高的交叉和遗传概率,使种群有较快的更新速度,加快了算法的搜索速度。在精度允许范围内,实现了算法快速、稳定地搜索。

2)仿真与实验结果表明,在不同的目标数量、不同的光斑半径以及不同的目标移动速度等情况下,本文所提基于贪心遗传算法的多光束扫描方法相较于传统的3种扫描方法,较大地缩短了扫描周期,并且有效地提高了目标捕获效率。其中,效率仿真结果整体提高了100%～300%,由于实现环境限制,实验结果提高了75%～150%。