双馈异步风电机组机侧转速控制器的设计与仿真研究
2023-10-07卢成志张银龙
张 骏,马 东,卢成志,张银龙
(华电电力科学研究院有限公司,杭州 310030)
0 引言
为落实中国节能减排目标,近年来中国风电机组装机容量快速增长,在总装机量中占比不断提升。根据中国电力企业联合会发布的2023年1—2月电力工业运行简况,截至2023年2月,中国风电机组装机容量为3.7亿kW,占总装机量的14.20%[1-2]。目前大规模并网运行的风电机组可分为两类:永磁直驱风电机组(PMSG)和双馈异步风电机组(DFIG)。DFIG由于其发电机(绕线式)和变流器造价低廉,在额定功率为2 MW及以下的风电机组类型中广泛使用。
DFIG在不同风速段的控制目标也略有不同。在切入风速附近(对于1.5 MW风电机组,风速一般为3.0~4.5 m/s)DFIG控制方式为恒转速控制(转速为1000 r/min),此时DFIG保持最低并网转速(控制I段);当风速(一般为4.5~9.0 m/s)略高于切入风速且略低于额定风速时,DFIG控制方式为恒定风能利用系数Cp控制,此时风轮转速随着风速的变化,而变化保持其最大风能利用系数Cp,max值不变(转速范围为1000~1800 r/min),从而使风轮捕获的能量最大(控制II段);当风速在额定风速附近时(一般为9~11 m/s),此时DFIG保持额定转速(1800 r/min)运行(控制III段);当风速高于额定风速(11 m/s)时,此时DFIG为依然保持额定转速(1800 r/min)恒功率运行(控制IV段)。
由于风资源较好的地区风能开发已趋于饱和,同时随着平价与竞价上网时代的到来,提升风电机组在低风速下的发电效率具有重要意义[3]。DFIG在控制II段(低风速段)通过调节发电机转矩使风轮按照最佳叶尖速比运行,跟踪最佳风能利用系数,提升风能利用率[4-5]。由于在电气结构上,DFIG的定子绕组直接与电网相连,机侧(即转子侧)通过变流器与电网相连,可通过调节转子侧变流器输出的频率和电流幅值控制DFIG转速[6]。所以,目前大多数主机厂家在控制II段主要采用查表法,主控系统将不同转速对应的转矩下放至变流器,由变流器调节转子侧电流大小,以实现对DFIG的转速控制。所以网侧变流器作为DFIG转速控制的核心部件,其控制方法和控制参数的选择极其关键。
本文在建立DFIG数学模型的基础上,采用传统PI矢量控制技术实现DFIG转速控制,并利用典型Ⅰ型系统参数设计方法优化控制器参数,同时结合Simulink仿真软件对该方法设计得到的参数进行仿真验证。
1 DFIG数学建模
由于双馈发电机具有非线性、强耦合的特性,所以为实现DFIG转速控制,必须构建DFIG动态数学模型。DFIG的转子侧电气原理如图1所示。图中:ur、ir为转子侧电压、电流,us、is分别为定子侧电压、电流,Q1~Q3、Q1′~Q3′均为绝缘栅双极型晶体管,C1为电容。
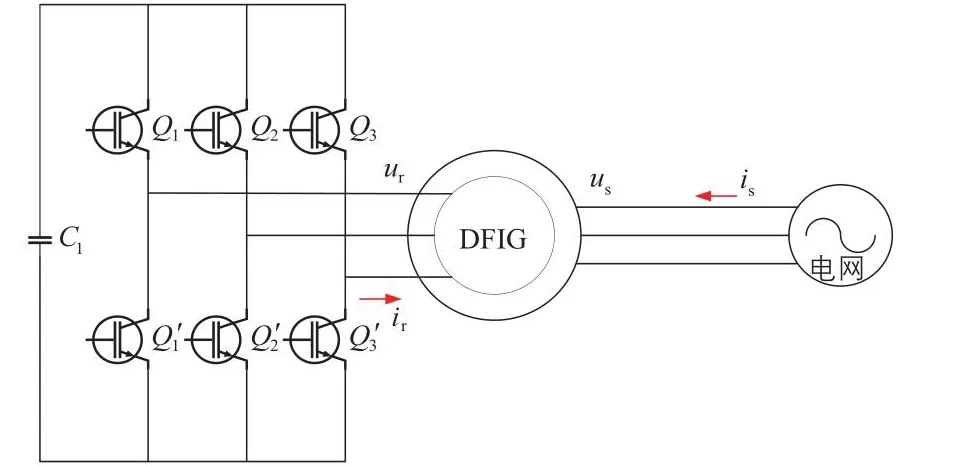
图1 DFIG转子侧电气原理图Fig.1 Electrical schematic diagram of rotor side of DFIG
由于传统的PI控制方式一般只能无静差跟踪阶跃信号,所以需将机侧三相静止坐标系下的方程转换为两相同步旋转坐标方程,DFIG定子侧数学模型为[5,7]:
式中:usd、isd和usq、isq分别为定子d轴和q轴的电压、电流分量;Rs为定子各相绕组电阻;ψsd、ψsq分别为定子磁链d轴、q轴分量;ωs为同步转速的电角速度。
定子磁链d轴、q轴分量的计算式为:
式中:Lm为励磁电感;Ls为定子漏感和励磁电感之和;ird、irq分别为转子d轴和q轴的电流分量。
DFIG转子侧数学模型为:
式中:urd、urq分别为转子d轴和q轴的电压分量;Rr为转子各相绕组电阻;ωm为转子的电角速度;ψrd、ψrq分别为转子磁链d轴、q轴分量。
转子磁链d轴、q轴分量的计算式为:
式中:Lr为转子漏感和励磁电感之和。
电磁转矩Te及运动方程为:
式中:TL为拖动转矩;J为转动惯量;np为磁极对数;Ωr为转子机械角速度。
目前DFIG转速控制方式一般采用基于定子磁链定向的矢量控制技术,将同步旋转坐标系的d轴定位于定子磁链空间矢量ψs,ψs与d轴重合,因此在q轴上的分量为0,表达式为:
由于目前兆瓦级风电机组定子侧电阻较小,可忽略不计,取值为零,则其定子侧电压方程可简化为:
式中:Vs为usq的幅值。
转子在d轴、q轴上的电压方程为:
其中:
电磁转矩方程:
定子侧有功、无功时的功率Ps、Qs的表达式为方程分别为:
式中:im为定子侧电流幅值。
2 控制器参数优化设计
由式(17)~(19)可得出,在定子磁链定向的同步旋转坐标系下电磁转矩大小仅取决于转子侧q轴的电流分量,定子侧无功功率取决于转子侧d轴的电流分量。因此,本文通过调节转子电压的方式来控制转子侧电流,从而调节发电机转速和定子侧无功功率。
从式(14)、式(15)可以发现:控制项urd、urq和被控项ird、irq分别存在耦合项(下文公式中的*代表其控制的参考量),为消除耦合项的影响,采用PI前馈解耦控制,其控制方程为[8]:
式中:kp为比例参数;ki为积分参数;s为拉普拉斯算子。
将式(19)、式(20)带入式(14)、式(15),且在稳态的情况下ψs的导数为零,可得:
从式(22)、式(23)可以看出:通过引入电流反馈和耦合项的前馈控制,可实现对转子侧电流的无静差控制。
在变流器控制中引入延迟环节T=0.5Ts(其中,Ts为正弦脉宽调制(SPWM)开关时间),则转子侧电流内环(d、q轴一致)的控制框图如图2所示。图中:τi为PI控制器参数,id为d轴或r轴转子侧电流。

图2 转子侧电流内环的控制框图Fig.2 Loop control block diagram of rotor side current inner
将其中电流采样环节和延迟环节合并,并忽略电流闭环函数(S)的高次项后对控制框图简化如图3所示。

图3 转子侧电流内环的简化控制框图Fig.3 Simplified control block diagram of rotor side current inner loop
其开环传递函数为:
一般电流控制环要求快速的跟随性,因此可以按照典型I型系统设计,令则系统的开环传递函数可进一步简化为:
按照“二阶最佳系统”进行参数整定,令阻尼系数ξ=0.707、时间常数KT=0.5[7],可得到:
由于目前变流器开关频率fsw足够高,SPWM开关时间将很小,所以电流内环闭环函数可简化为一个小惯性环节,其具有较快的动态响应特性。电流内环闭环函数Gci(S)可表示为:
3 仿真验证过程及结论
目前大多数变速恒频风电机组在恒风能利用系数运行过程中采用查表法,主控系统根据风电机组的转速将参考转矩Tref、参考无功功率Qref发送至变流器,由变流器通过调节机侧电压和频率来控制风电机组转速实现恒风能利用系数运行。
本文主要针对这种控制模式,利用Simulink仿真软件对当前常见的1.5 MW DFIG参数对变流器电流内环控制进行仿真验证。DFIG的转子侧完整控制框图如图4所示,图中:θm为电网的电角速,θs为发电侧的电角速。1.5 MW的DFIG基本参数如表1所示。主控系统采用查表法,其转速和转矩的对应关系如表2所示。

表1 1.5 MW DFIG基本参数Table 1 Basic parameters of 1.5 MW DFIG

表2 1.5 MW DFIG采用查表法时的参数Table 2 Parameters of 1.5 MW DFIG using lookup table method

图4 转子侧完整控制框图Fig.4 Control block diagram of rotor side
图5是DFIG转速仿真图,从图5可以看出:DFIG从转速0 r/min到并网转速1000 r/min约为0.5 s。为模拟DFIG在大风环境中风速突变的情况,人为设置在6 s时DFIG输入转矩由0.3Te突变至0.5Te,经过5 s后,DFIG转速稳定在1650 r/min,DFIG转矩仿真图如图6所示,图中:Twin为DFIG风轮输入转矩。
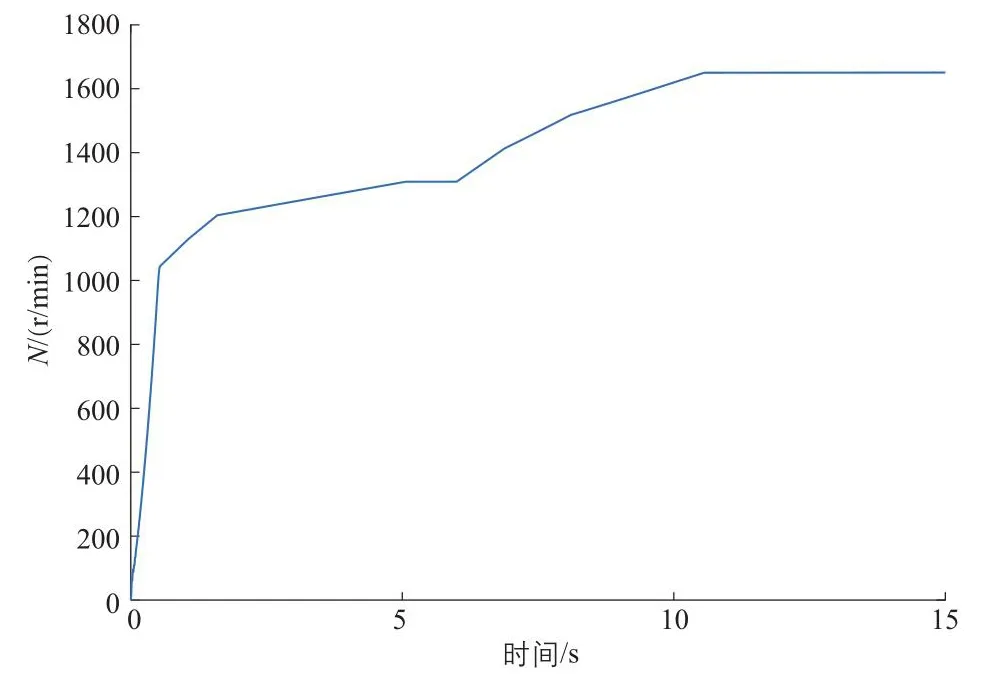
图5 DFIG的转速仿真图Fig.5 Simulation diagram of speed of DFIG
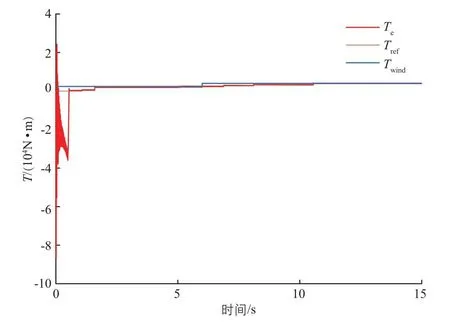
图6 DFIG的转矩仿真图Fig.6 Simulation diagram of torque DFIG
从图5、图6可以看出:电磁转矩数值跟随主控系统下发给变流器的目标转矩数值实时变化;随着转速的上升,电磁转矩和主控系统下发给变流器的目标转矩都呈阶梯式变化,最后逐渐趋于稳定,稳定在风轮输入转矩的数值,从而转速达到稳定。
图7是DFIG转子侧电流(d、q轴)仿真图,由于人为设置定子侧无功功率为零,所以转子侧电流d轴分量的计算值为零,转子侧电流q轴分量由主控系统下放的转矩通过式(17)计算得出。

图7 DFIG转子侧电流仿真图Fig.7 Simulation diagram of current of otor DFIG
从图7可以看出:无论是转子侧电流d轴或q轴电流,都可以快速跟踪主控系统给定值,即使由于输入转矩突变,控制器也能使系统重新达到平衡。
4 结论
本文研究了DFIG变流器机侧控制器设计方法及参数整定计算方法,通过坐标变换将转子侧电流从三相静止坐标系数学模型转换成d、q轴同步旋转坐标系数学模型,利用PI控制器实现风电机组的转矩控制,并利用Simulink仿真软件查表法进行仿真验证,得出以下结论:
1) 利用PI控制器可实现风电机组转速-转矩控制,该控制器具快速性和抗扰动性。其发电机转子侧电流理论上可实现无静差跟踪。
2) 控制器设计过程中需要将转子侧三相静止坐标系下的电流值转换为两相同步旋转坐标系下的电流值,在实际应用中对变流器数字处理芯片的性能要求较高。
3) 在定子磁链定向的矢量控制方法中,其磁链定向的准确性会直接影响控制器性能,本文仿真采用的是电网电压定向的磁链观测器,在理想电网的情况下该方法能准确反映磁链空间矢量情况,但在电网故障的情况下定子会感应出磁链的自由分量,从而影响磁链观测器的结果。
4) 由于采用查表法的控制方式,一方面,DFIG转矩成阶梯状上升,导致DFIG转速无法实时跟踪风速的变化,从而影响DFIG能效;另一方面,在转矩变化的附近,由于风速小幅度变化,可能导致转速出现震荡情况。
