基于液电馈能悬架的车身姿态控制研究

2023-10-07唐宇飞武志斐张翠平王增荣

机床与液压 2023年17期

唐宇飞，武志斐，张翠平，王增荣

(太原理工大学机械与运载工程学院，山西太原 030024)

0 前言

传统悬架系统各元件特性不可调，导致汽车在复杂工况下行驶时车身姿态无法调整，难以满足乘员乘坐舒适性要求。车辆行驶过程中，悬架运动状态与车身姿态密切相关[1]，液电馈能型悬架除了回收车身振动能量，还能通过改变阻尼力调节车身姿态，提升车辆的操纵稳定性和乘坐舒适性[2-6]。因此，越来越多的学者关注车辆馈能悬架及车身姿态控制。寇发荣等[7-8]提出一种电磁复合馈能悬架，设计了主环与内环结合的半主动控制策略，以提高舒适性与安全性，并通过设计升降压控制规则提高能量回收率。汪若尘等[9-10]为了实现车辆全局工况最优，设计了具有3种模式的馈能悬架，在改善车辆行驶平顺性及操纵稳定性的同时回收振动能量。邹俊逸等[11]研究了不同工况下液电馈能减振器对车辆操纵稳定性的影响。CASAVOLA等[12-13]基于多目标控制设计策略，不仅改善了车辆在常规道路上的操控性和乘坐舒适性，还提升了能量回收率。张晗等人[14]基于液电式馈能半主动悬架系统，设计了线性最优控制器，提升了悬架馈能功率，但降低了车辆综合性能。吴麟麟等[15]设计了一种姿态补偿的整车悬架控制方法，通过改变悬架系统减振器的输出阻尼力，达到对车身姿态的控制，有效抑制了行驶过程中的车身姿态恶化。

上述研究表明，国内外学者针对液电馈能悬架和车身姿态控制做了大量研究，但液电馈能悬架对整车性能影响的理论与试验研究不足，悬架特性与整车姿态的耦合机制尚不明确，缺少装配液电馈能悬架的整车车身姿态研究。

针对上述问题，本文作者基于液电式馈能悬架，引入馈能电路模块，根据车身姿态、悬架阻尼力与馈能电路电流的耦合关系，设计恒流控制的馈能电路，以改善液电馈能悬架的动力学性能，提升车身姿态稳定性，并进行实车试验验证模型和控制方法的有效性。

1 液电式馈能悬架

1.1 悬架结构与工作原理

液电式馈能悬架是集液压整流系统与馈能系统于一体的机电耦合系统，主要部件为液压元件、整流桥、单向阀、蓄能器以及发电机等。工作原理如图1所示：当馈能悬架伸缩运动时，液压油液在液压缸中往复运动，通过半桥式整流桥实现油液的定向流动，驱动液压马达单向旋转并带动发电机工作，产生电能并储存。

图1 液电馈能悬架工作原理

1.2 悬架馈能电路

馈能电路模块主要由液压马达、发电机和外接负载构成，具体结构如图2所示。液压管路输入的液压油使液压马达旋转，通过联轴器带动发电机旋转产生电能并将产生的电能存储到蓄电池中。

图2 馈能电路模型

由图2可知液压马达旋转带动发电机发电时，转速与输出力矩的关系为

(1)

式中：n、Tm分别为液压马达输出轴转速与输出力矩；Qm、q分别为液压马达的流量与排量；Δpm为液压马达进出口油液压差；ηv、ηm分别为液压马达的容积效率和机械效率。

当发电机通过联轴器与液压马达相连旋转时，输出电压Uemf与输入转矩Te满足：

(2)

式中：ke、kt分别为与发电机结构相关的转速常数与转矩常数；Jg为马达-电机耦合系统的等效转动惯量；I为发电机输出电流。

结合图2馈能电路模型以及基尔霍夫定律可得如下关系式：

(3)

联立公式(1)—(3)可得发电机的输出电流I如式(4)所示：

(4)

式中：D为工作缸直径；drod为活塞杆直径；Rin、Rex分别为发电机内阻和外接负载；v(t)为t时刻活塞杆的运动速度。由式(4)可知，在机械结构参数确定的情况下，馈能电路电流取决于活塞杆的运动速度和外接负载阻值的大小。

1.3 馈能悬架阻尼力模型

液电式馈能悬架阻尼力分为液压油压力降低产生的固有阻尼力以及液压马达带动发电机工作的旋转阻力，即等效可控阻尼力。基于图1所示的悬架工作原理，建立部分液压元件的数学模型，阐述悬架阻尼力的理论公式，进而揭示车身姿态与阻尼力的耦合关系。

考虑液压油在管路中流动及流经单向阀所产生的压力损失，采用小孔节流公式得出单向阀与液压管路压降表达式分别为

(5)

式中：Δpvi、Δppi分别为单向阀与液压管路压降；ρ为油液密度；Cd为流量系数；kvi、Bvi、Avi分别为单向阀阀片边缘的刚度、周长、面积，其中Bvi=πdvi，dvi为阀片的直径；Qvi为流经单向阀的流量，i=1，2；Qpi为流经管路的流量；μ为油液的动力黏度；Lpi、dpi分别为液压管路的长度与直径。

根据理想气体性质可得t时刻蓄能器内的气体压力如式(6)所示：

(6)

式中：p0、V0分别为初始状态下蓄能器内气体压力和体积；pt、Vt分别为t时刻蓄能器内气体的压力和体积；m为多变指数；Ar为活塞杆面积；v(t)为t时刻活塞杆的运动速度。

在液压缸伸张与压缩过程中，悬架的总阻尼力如式(7)所示：

F=Fsa+Fp

(7)

式中：Fsa为馈能悬架的可控阻尼力；Fp为馈能悬架的固有阻尼力。

其中，液电馈能悬架伸张与压缩过程的可控阻尼力如式(8)所示：

(8)

液电馈能悬架伸张与压缩过程的可控阻尼力Fp如式(9)所示：

(9)

将公式(8)与公式(9)代入公式(7)即可得液压缸伸张与压缩过程液电馈能悬架阻尼力，为下面的仿真试验提供理论依据。

1.4 整车系统动力学模型

为探索液电馈能悬架与车身姿态的耦合机制，将液电馈能悬架理论模型与十四自由度整车动力学模型耦合为如图3所示的模型。其中，十四自由度包括车身的3个平移自由度和3个转动自由度，4个簧下质量的垂直跳动自由度及其自旋自由度。文中以液电馈能悬架的阻尼力替换原有整车动力学模型中的阻尼力，获得液电馈能悬架整车系统模型。在此基础上引入恒流控制，通过控制馈能电路电流，改变液电馈能悬架的可控阻尼力，进而实现液电馈能悬架恒流控制与车身姿态的耦合控制。

图3 整车动力学模型

当俯仰角和侧倾角在较小范围内时，车身4个端点处垂向位移近似为

(10)

式中：zbA、zbB、zbC、zbD为车身4个端点的垂直位移；zb为车身质心处的垂直位移；L1、L2分别为车身质心到前后桥的距离；θ、φ分别为车身的俯仰角与侧倾角；Wf、Wr分别为车身质心到左右车轮的距离，两者相等，且Wf=Wr=W。

文中着重研究车辆的俯仰、侧倾及横摆运动，根据十四自由度动力学模型，得到车身俯仰角、侧倾角与悬架阻尼力的耦合关系以及车身横摆角速度的运动学方程。

车身俯仰运动如式(11)所示：

L1[FA+ksA(zwA-zbA)+FB+ksB(zwB-zbB)]

(11)

车身侧倾运动如式(12)所示：

(12)

车身横摆运动如式(13)所示：

FLB)sinδf]L1-[(FSC+FSD)cosδr+(FLC+

FLD)sinδr]L2+[(FLB-FLA)cosδf+(FSA-FSB)sinδf]·

(13)

式中：ksi为悬架刚度；zwi为4个车轮的位移；Fi为悬架的阻尼力；FSi、FLi分别为4个车轮的侧向力和纵向力(i=A、B、C、D)；Ix、Iy分别为围绕x、y轴的弹簧质量惯性矩；γ为车辆的偏航角；δf、δr分别为前后轮的转向角。

整车模型主要参数如表1所示。

表1 整车模型主要参数

2 恒流控制设计

在液电馈能悬架系统中，液压马达与发电机相互耦合、相互影响，因此，可通过控制馈能电路电流实现悬架整体性能协调。与恒压控制方法相比，具有系统稳定性强、快速限制电流的特点，可将电流限制在特定的工作范围。恒流控制方法流程如图4所示。

图4 恒流控制方法流程

由发电机的工作原理与馈能电路布置，可得：

(14)

式中：Pe为发电机功率；P为发电机输出功率；Pc为发电机损耗功率；Ie为液电馈能悬架馈能电路电流。

发电机的输出功率如式(15)所示：

P=U·Ie

(15)

式中：U为发电机两端电压。根据式(15)和(16)得：

(16)

由式(16)可知，所设计的恒流控制方法，通过调节外接电阻阻值Rex实现馈能电路电流的实时控制，而电流又与悬架阻尼力相关，因此，通过调节电阻控制电流可实现对悬架阻尼力的控制，改善悬架整体性能，进而控制车身姿态。

3 整车仿真分析

3.1 馈能电路电流分析

基于上述控制原理，以悬架馈能电路为研究对象，基于AMESim搭建仿真模型，预设参考电流值范围为0.2～2 A，仿真得到馈能电路实际感应电流如图5所示。

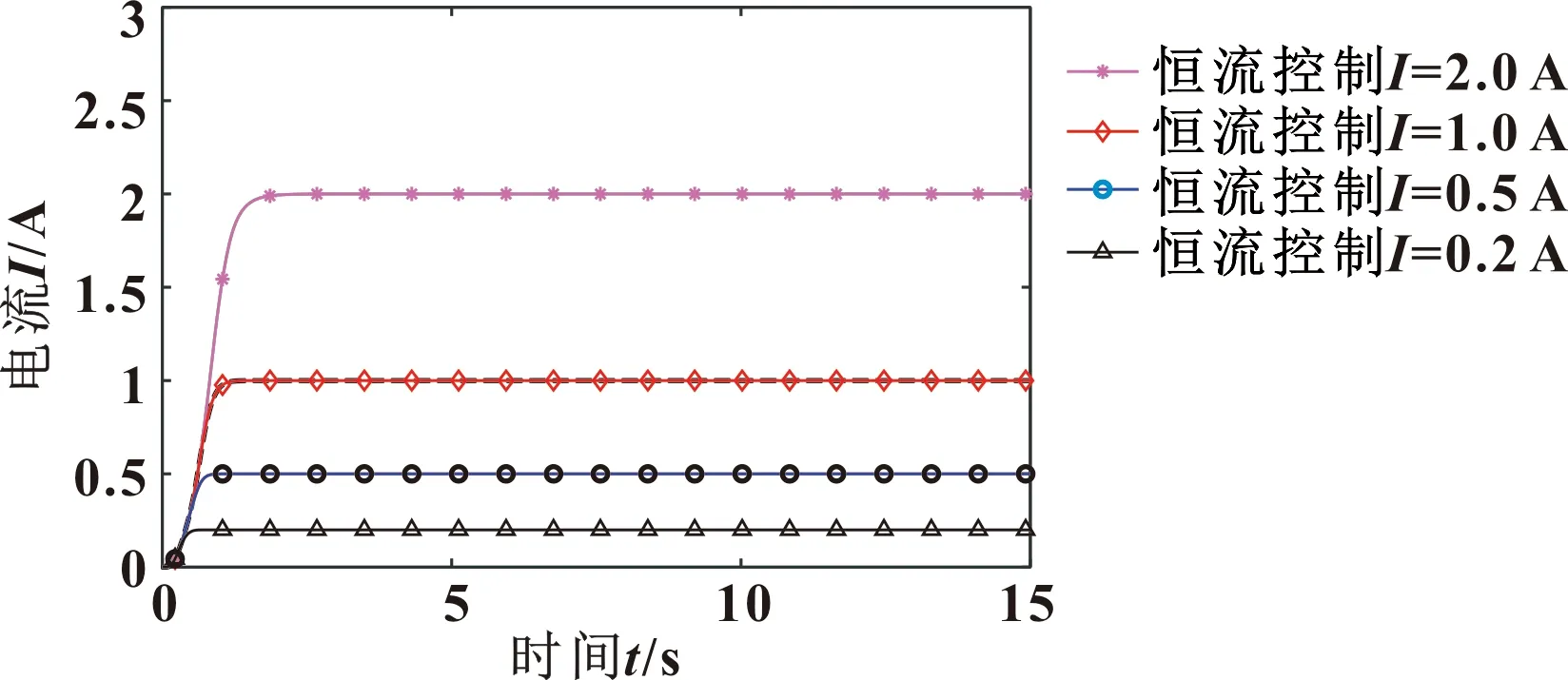
图5 恒流控制馈能电路电流

由图5可知：在电流设定范围内，馈能电路电流实际值可快速改变至目标值，随着电流的增大，馈能电路达到设定电流所需要的时间逐渐增加。在馈能悬架进行减振时，馈能电路电流能实现较长时间的恒定无波动，体现恒流控制的优点。

3.2 蛇行工况仿真分析

为验证恒流控制的有效性与合理性，进行整车动力学仿真，仿真参数如表1所示，以30 km/h的车速在如图6所示的蛇行路线行驶，提取车身侧倾角、俯仰角和横摆角速度为评价指标，进行连续转向工况下液电馈能悬架恒流控制对车身姿态的影响研究。

图6 蛇行试验路线

仿真得到车身侧倾角、俯仰角与横摆角速度的时域响应如图7—9所示。由图7可知恒流控制液电馈能悬架的车身侧倾角幅值相对传统悬架减小，但仍具有波动性。

图7 蛇行工况车身侧倾角

相比于传统悬架，车身侧倾角优化效果显著，但在连续转向工况下，液电馈能悬架抵抗侧倾的能力逐渐减弱，甚至产生响应迟滞现象。由此可知恒流控制需要根据实际运行工况进行控制电流的调整，保证抵抗车身侧倾运动的能力始终处于最优。

由图8可知，前20 s过渡主要是避免其他参数如液电馈能悬架阻尼波动导致的影响，液电馈能悬架抗俯仰运动的能力随着连续转向工况的进行逐渐降低，车身俯仰角不断增大，蛇行工况结束时车身俯仰角存在振荡现象。

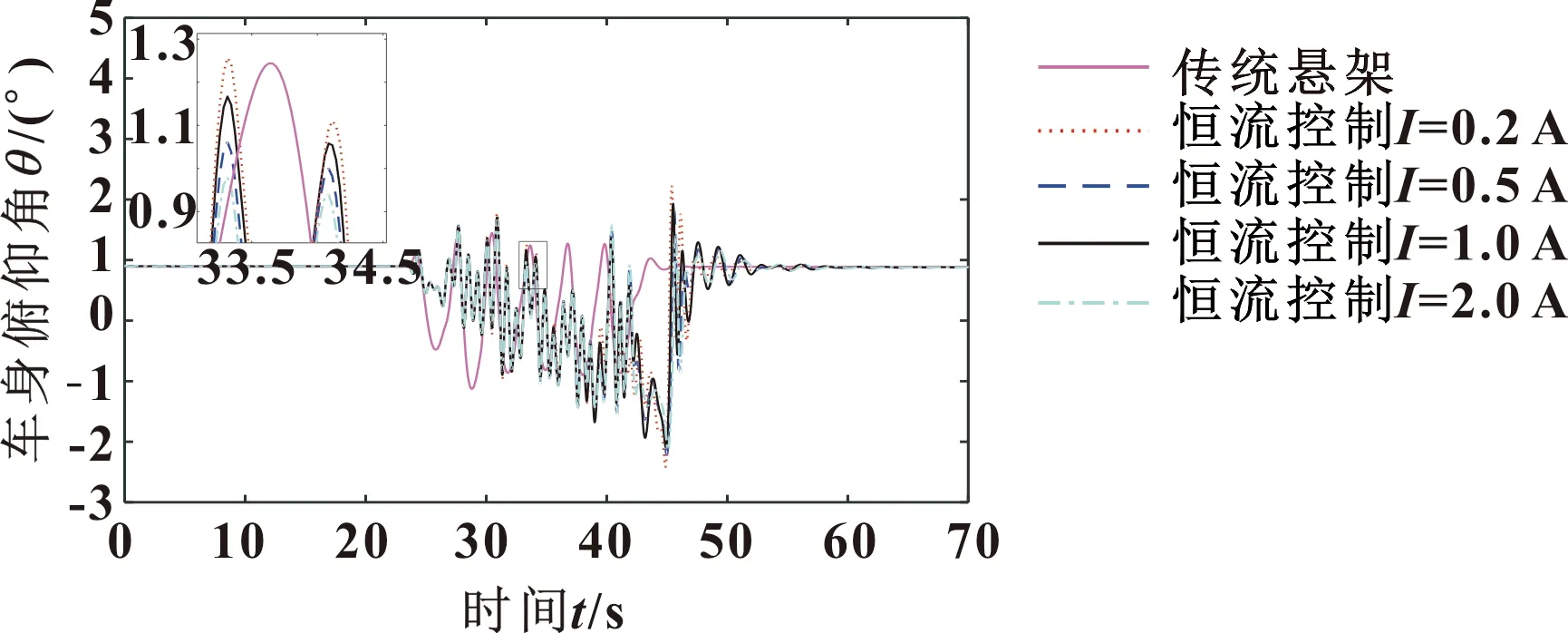
图8 蛇行工况车身俯仰角

由图9可知：液电馈能悬架在恒流控制状态下，车身横摆角速度与控制电流成反比关系，相比传统悬架，横摆角速度有所增大。

为更有效评价液电馈能悬架系统对车身姿态的影响，应用上述3种评价指标分析车辆在蛇行工况下的响应，各指标的均方根值(Root Mean Square，RMS)如表2所示。

表2 蛇行工况车身姿态指标RMS

由表2可知：车身侧倾角随着控制电流的增大逐渐减小，在电流为2 A时参数达到最优，在电流控制范围内，侧倾角RMS值减少幅度分别为1.38%、1.91%和2.48%，优化幅度最大为5.66%，且与传统悬架相比，液电馈能悬架车身侧倾角RMS改善了32%。

液电馈能悬架车身俯仰角与横摆角速度也随控制电流的增大逐渐减小，其RMS最优减小幅度分别为2.73%和4.69%，其中，俯仰角RMS峰值比传统悬架稍大，但最优参数下俯仰角RMS改善了1.67%；同时，横摆角速度与传统悬架系统相比发生一定恶化，但液电式馈能悬架系统比传统悬架系统存在明显优势，侧倾角和俯仰角得到改善，其中侧倾角改善效果最为显著。综上，所设计的控制方法提升了液电馈能悬架系统的整体性能，改善了车身姿态稳定性。

4 整车试验

为验证所提控制方法的有效性，将馈能悬架实现整车应用，进行液电馈能悬架实车道路试验，将仿真与试验结果对比分析。根据GB/T 6323—2014《汽车操纵稳定性试验方法》，在蛇行试验工况下，车辆必须在干燥的水泥或者沥青路面行驶，任何方向上的坡度最大不能超过2%，相对湿度小于95%。试验场地设置标桩10根，间距30 m，汽车在行驶过程中，车速保持恒定为30 km/h。

整车试验系统及布置形式见图10，试验仪器主要包括：MOB型液压缸、CIT-04标准直通单向阀、NXQ蓄能器、丹弗斯OMM32液压马达、稀土永磁直流发电机、数据采集设备和维特智能BWT901CL-TTL陀螺仪传感器，其中，液电馈能悬架的液压系统与馈能系统布置在试验车辆后备厢内，液压缸安装在试验车辆原减振器位置，陀螺仪传感器固定在车身底部中心位置用于检测车身姿态。

图10 整车试验系统

蛇行试验行驶下车身姿态试验结果如图11—图13所示，可以看出：蛇行试验测试过程中车身俯仰角、侧倾角及横向角速度均呈正弦波形状，在电流变化范围内随电流的增大而逐渐减小，变化趋势与仿真分析得出的电流与车身姿态关系一致，验证了理论模型的有效性。

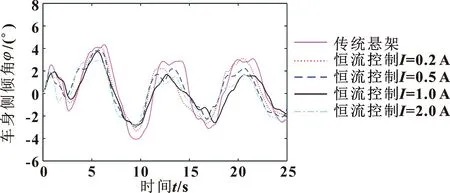
图11 蛇行试验车身侧倾角

由图11和表3可知，车身侧倾角相较于俯仰角变化幅度更大，车辆的侧倾运动影响更为明显，表明在蛇行试验工况下车辆姿态更易受侧倾运动影响。当电流增至2 A时，侧倾角减小41.78%，相比于传统悬架，液电馈能悬架侧倾角RMS减少幅度最大为34.75%，这与仿真所得出的侧倾角改善趋势一致，表明建立的理论与仿真模型的正确性。

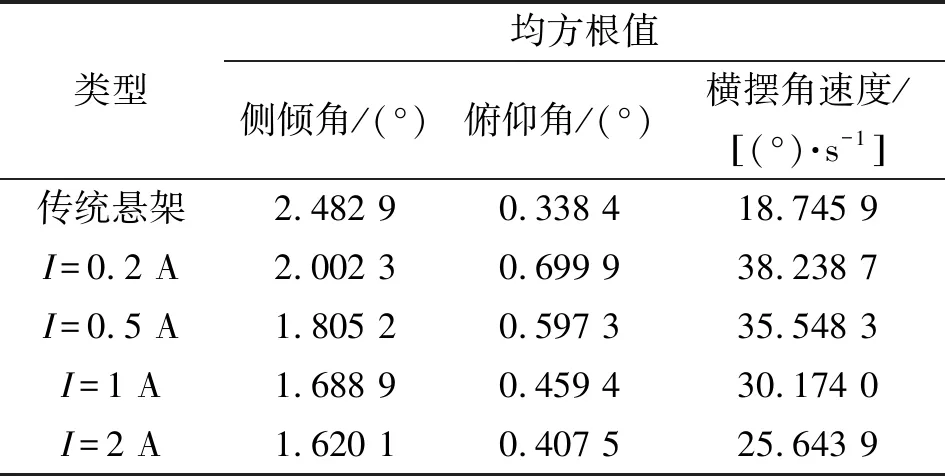
表3 实车蛇行试验车身姿态指标RMS

同理，为更有效评价液电馈能悬架系统对车身姿态的影响，车辆在蛇行试验下各评价指标的均方根值如表3所示。

通过调整负载阻值可改变液电馈能悬架馈能电流，同时也可改变悬架阻尼力，衰减车轮与车身之间的垂直振动，改善车身俯仰角。

由图12与表3可知，车辆俯仰角在0～5 s内显著波动，这是因为车辆突然启动时产生抬头效应，导致俯仰角较大变化，且每当车辆绕桩转弯时，俯仰角均会产生一个峰值。当电流从0.2 A增加至2 A时，车身俯仰角从0.7°减少至0.41°，减少幅度为41.43%，改善效果显著。

图12 蛇行试验车身俯仰角

由图13可知：车辆连续转弯下，随着电流增大，车身横摆角速度逐渐降低，表明通过调节馈能回路电流可改善车辆的横摆运动，与仿真结果基本一致。相比于传统悬架，液电馈能悬架系统在蛇行测试下的车身俯仰角与车身横摆角速度均有增大，车辆乘坐舒适性略微降低，但总体来说，液电馈能悬架可显著提升车辆抗侧倾能力，改善车身姿态稳定性，在一定程度上提升了车辆整体动态性能。