正流量液压挖掘机行走跑偏诊断序列决策
2023-10-07张金戈罗南岚郑海涛王高龙章浩
张金戈,罗南岚,郑海涛,王高龙,章浩
(山河智能装备股份有限公司,湖南长沙 410100)
0 前言
挖掘机被广泛应用于工程建设、矿山开采等与民生生活、国家建设息息相关的领域,是一种重要的工程作业装备[1]。正流量液压挖掘机具有操作性好、系统响应快、节流损失小等优势[2],是当代主流挖掘机之一。
在任何情况下,保证整机行走的直线性是对挖掘机行走液压系统的最基本要求[3]。若行走跑偏距离超出阈值,轻则影响操作性与作业效率,给施工企业带来巨大的经济损失,重则在特殊作业如斜坡作业、高处挖深时严重威胁驾驶员的生命安全。随着现代科学技术的进步,液压挖掘机液压系统的结构越来越复杂,加剧了维修难度[4]。因此,有必要对液压挖掘机行走跑偏的故障诊断序列进行研究。
故障树分析方法是一种故障诊断的有效方法,被广泛研究和应用[5-6]。传统故障树分析方法部件故障率、故障概率数据较少、难以精确获得,基于二态假设、不能适应实际系统存在的多种故障状态,难以精确描述系统故障机制[7-8]。T-S故障树分析方法[9]可以刻画任意形式的组合、多态等静态失效行为,相对于传统故障树具有更好的泛化能力[10],更适合应用于液压挖掘机这类复杂液压系统的故障诊断。
为此,本文作者研究一种基于T-S故障树的故障诊断最优序列多属性决策方法,将它应用于正流量液压挖掘机行走跑偏故障诊断,生成最优诊断序列,为维修维护提供重要依据。
1 基于T-S故障树的故障诊断最优序列多属性决策
1.1 T-S故障树分析方法
T-S故障树用T-S门描述事件联系,用一系列的规则量化事件对系统的影响,能描述不确定性事件间联系。图1是一个基本的T-S故障树。图中:y为顶事件;x1,x2,…,xn为基本事件;G为T-S门。上级事件y各失效状态的发生可能性可由下级事件x1,x2,…,xn通过T-S门规则描述。

图1 基本的T-S故障树


(1)
上级事件y处于故障状态yky时的概率为
(2)
重要度是评价基本事件对系统影响程度的指标,可量化基本事件对系统失效概率的贡献大小,在指导故障诊断的维修顺序时具有重大意义。概率重要度是重要度的一种,描述系统中某元件的状态变化引起系统故障概率变化的程度[11]。

(3)
利用T-S故障树分析方法得到各基本事件的概率重要度,反映了各基本事件对系统的影响程度,可作为生成故障诊断最优序列的重要依据。
1.2 基于专家综合评判的基本事件数据信息获取方法
专家综合评判是获取基本事件数据信息的一种有效工具,例如故障率[12]等。专家常常以语言值描述量的大小,例如大、中、小等。文中用一种基于专家综合评判的基本事件故障率获取方法,将描述基本事件故障率的语言值转化为梯形模糊隶属函数,进行定量计算。
梯形隶属函数具有形式简单、对数据信息要求低、准确有效的特点。梯形模糊数X用(m,a1,b1,a2,b2)表示,其中:m为模糊数支撑集的中心;a1和a2分别为左、右支撑半径;b1和b2分别为左、右模糊区。X的隶属函数μX(x)如图2所示。

图2 梯形模糊数X的隶属函数
由图2可知:
μX(x)=
(4)
用代表程度的语言值表达各专家的评价等级,将语言值用模糊数近似表示,文中选用的语言值梯形模糊数如图3所示。
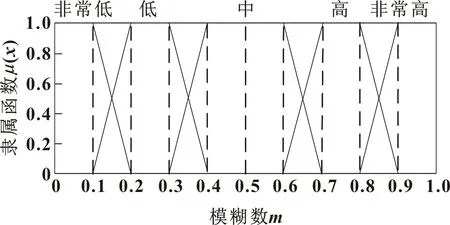
图3 语言值梯形模糊数
模糊数X=(m,a1,b1,a2,b2)是一个“亦此亦彼”的模糊值,难以量化。进行定量分析与定性比较时可把模糊数去模糊化,转化为一个清晰值,即模糊可能性值(FPS)。FPS代表了专家对某一事件发生可能性的信任度,文中应用左右模糊排序法[13]把模糊数转化为FPS。该方法定义最大模糊集fmax(x)和最小模糊集fmin(x)分别为
(5)
(6)
模糊数X的左右模糊可能性值δFPS,L(X)、δFPS,R(X)分别为
(7)
(8)
模糊数X的模糊可能性值δFPS(X)为
δFPS(X)=[δFPS,R(X)+1-δFPS,L(X)]/2
(9)
1.3 最优故障诊断序列多属性决策方法
故障诊断排序应综合考虑基本事件发生概率、在系统的重要程度、排查方法时长、代价等,属于多属性决策问题。为此,采用逼近理想解排序法(TOPSIS)[14]对最优故障诊断序列进行决策。
TOPSIS中心思想在于确定各项指标的理想解(最优方案)和负理想解(最差方案),然后求出各个方案与理想解、负理想解的加权欧氏距离,得出各方案与最优方案的接近程度,作为决策依据。
基于T-S故障树的故障诊断序列多属性决策的步骤为:
(1)建造诊断对象的T-S故障树
利用T-S故障树分析方法和基于专家综合评判的基本事件数据信息获取方法,求解各基本事件发生概率、概率重要度、搜索代价和花费时长等属性值。
(2)构建故障诊断序列多属性决策矩阵
定义基本事件x1,x2,…,xn的m项属性值(发生概率、概率重要度、搜索时长、花费代价等),基本事件xi的属性值用Yi={yi,1,yi,2,…,yi,j,…,yi,m}表示,构成决策矩阵Y=[yi,j]T。
为消除不同物理量纲对决策结果的影响,在进行决策前,需对各属性的数据进行规范化,若规范化矩阵Z=[zi,j]T,则

(10)
(3)确定理想解和负理想解

(11)
(12)
(4)计算各方案到理想解和负理想解的距离

(13)
(14)
(5)计算各方案综合评价指数
基本事件xi的综合评价指数用Ci表示,则:
(15)
将Ci按大小进行排序,Ci越大则在故障诊断序列中的优先级越靠前。
2 正流量液压挖掘机行走液压系统分析
2.1 正流量液压挖掘机行走液压系统
(1)液压传动原理
挖掘机行走液压系统如图4所示。
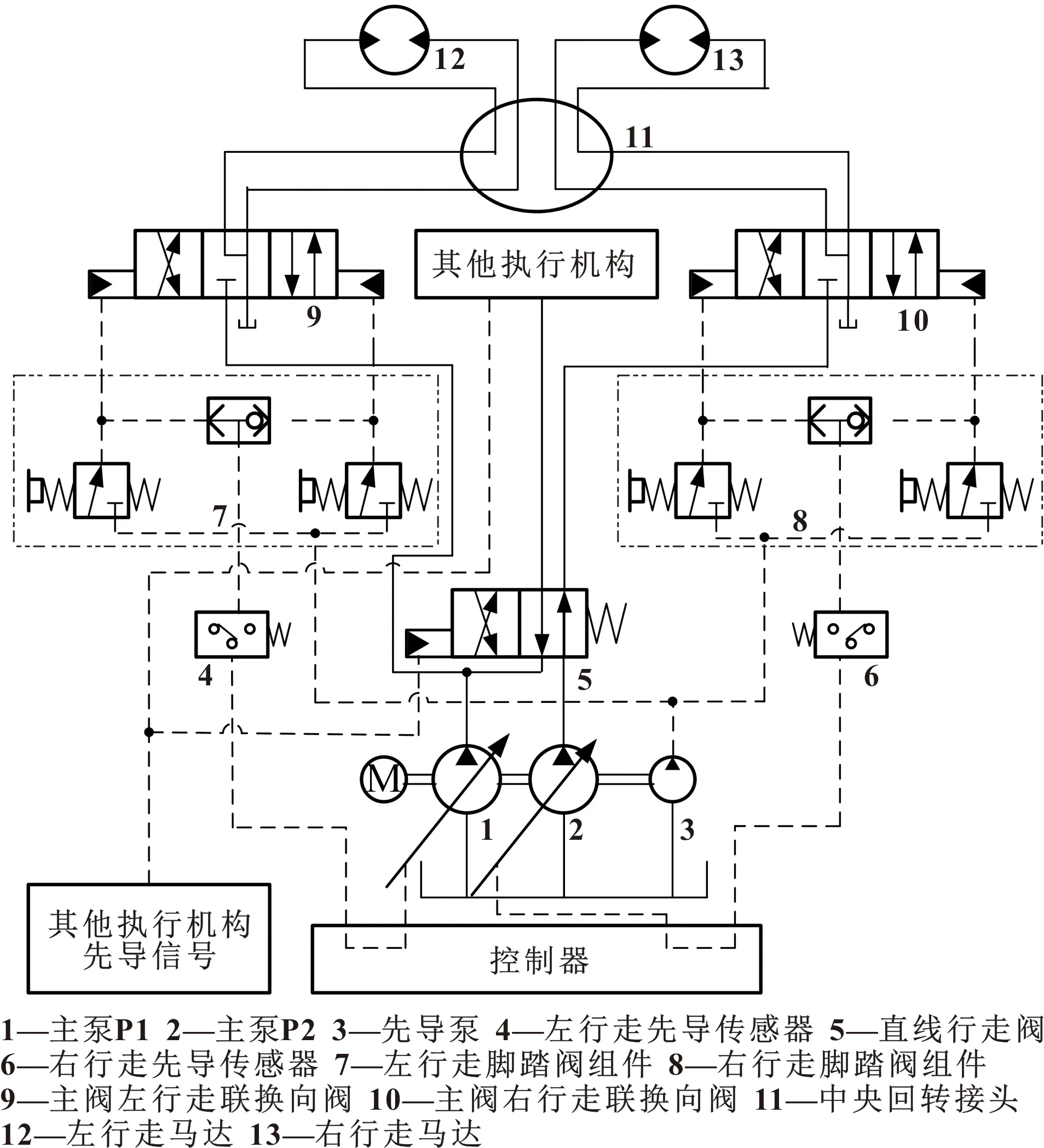
图4 液压挖掘机行走液压系统
挖掘机行走液压系统普遍采用双联主泵向液压系统提供工作流量,并用同轴齿轮泵作为先导泵向液压系统提供先导控制油源。
主泵由排量可调、转速相同的2个柱塞泵组成,从液压油箱吸取液压油,输送到主阀。有其他上车动作做行走时,直线行走阀左位工作,单泵P1供油;无其他上车动作做行走时,直线行走阀右位工作,泵P1、P2分别供油。液压油经主阀行走联换向阀后,由中央回转接头分配给左、右液压行走马达,输出为左右行驶速度。
(2)排量控制原理
正流量控制液压系统由操纵阀压力控制主泵排量。主控制器根据先导压力信号判断执行机构的流量需求,向主泵比例减压阀输出不同电流值控制比例减压阀输出不同压力值,通过变量伺服阀和变量执行液压缸控制主泵排量。正流量控制原理框图和主泵原理分别如图5、图6所示。

图5 正流量控制原理框图

图6 主泵原理
(3)行走马达原理
一种行走马达液压原理如图7所示。

图7 行走马达液压原理
该行走马达由防止外力引起马达旋转导致失控的平衡阀和制动解锁装置、启动与制动时起缓冲作用以及对回路起限压作用的安全阀、对回转马达起变排量作用的高低速切换阀等组成。
2.2 正流量液压挖掘机行走跑偏原因分析
为保证正流量液压挖掘机双边行走速度相同,左右行走马达必须同时满足:(1)响应时间相同;(2)输入流量相同;(3)排量相同。结合正流量液压挖掘机行走液压系统原理,造成行走跑偏的失效模式和排查方法见表1。

表1 各元件失效模式和排查方法
3 正流量液压挖掘机行走跑偏最优诊断序列
3.1 基本事件信息评价
利用专家评价系统,选择基本事件发生概率、搜索代价和搜索时长3种属性对各基本事件进行评价。各基本事件信息评价值见表2。
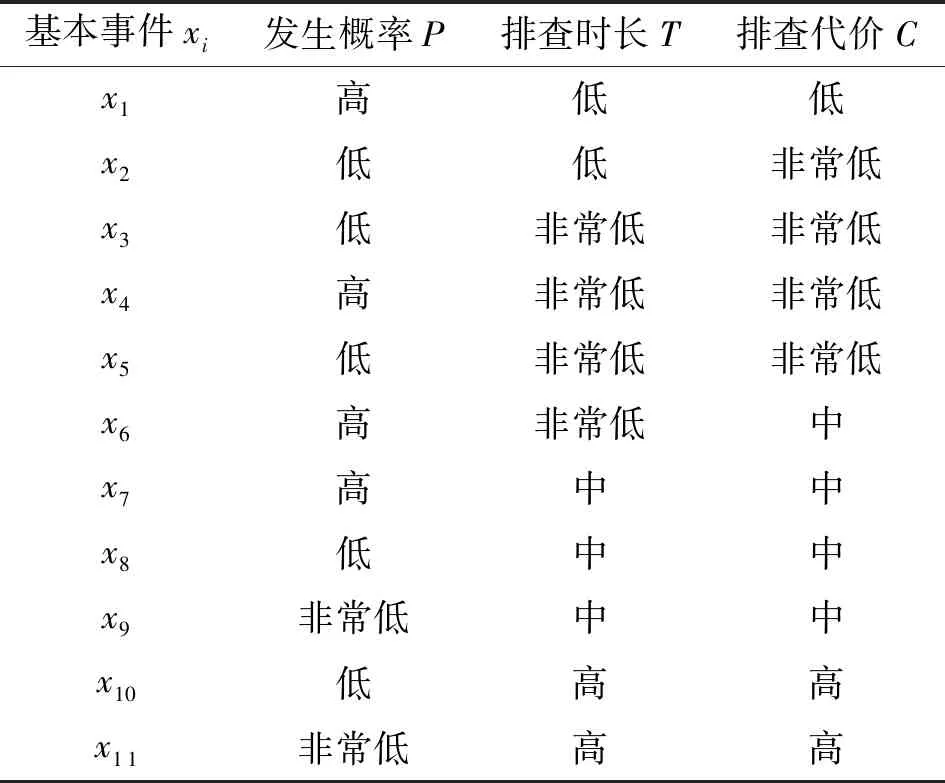
表2 基本事件信息评价值
将表2按图3转化为梯形模糊数,再利用式(4)—(9)求解各基本事件FPS值见表3。

表3 基本事件FPS值
3.2 T-S故障树构建及分析
构建正流量液压挖掘机行走跑偏T-S故障树如图8所示,图中各符号含义见表1。
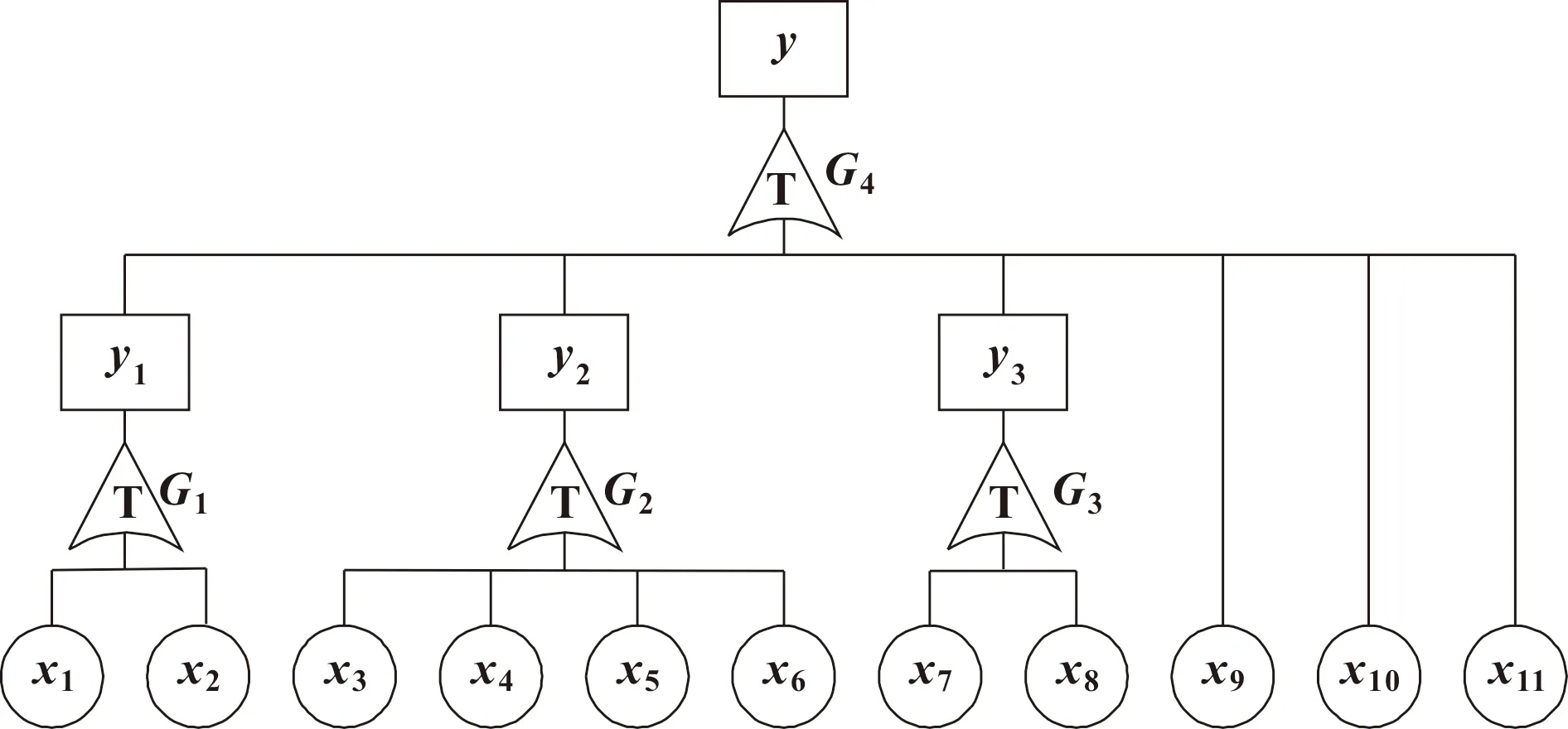
图8 正流量液压挖掘机行走跑偏T-S故障树
G1(G3)门中,任何一个下级事件发生都会引起上级事件发生,例如双脚踏阀输出压力差别超出阈值,则必会引起行走跑偏,因此G1(G3)门规则见表4。

表4 G1(G3)门规则
G2门中,若变量控制机构故障或溢流阀故障则会引起行走跑偏。若平衡阀阀芯卡滞或制动解锁节流孔堵塞,则可能是液压油清洁度不达标导致,这种情况下左右行走马达可能同时表现出平衡阀阀芯卡滞或制动解锁节流孔堵塞,反而不会引起行走跑偏。鉴于此,G2门规则见表5。
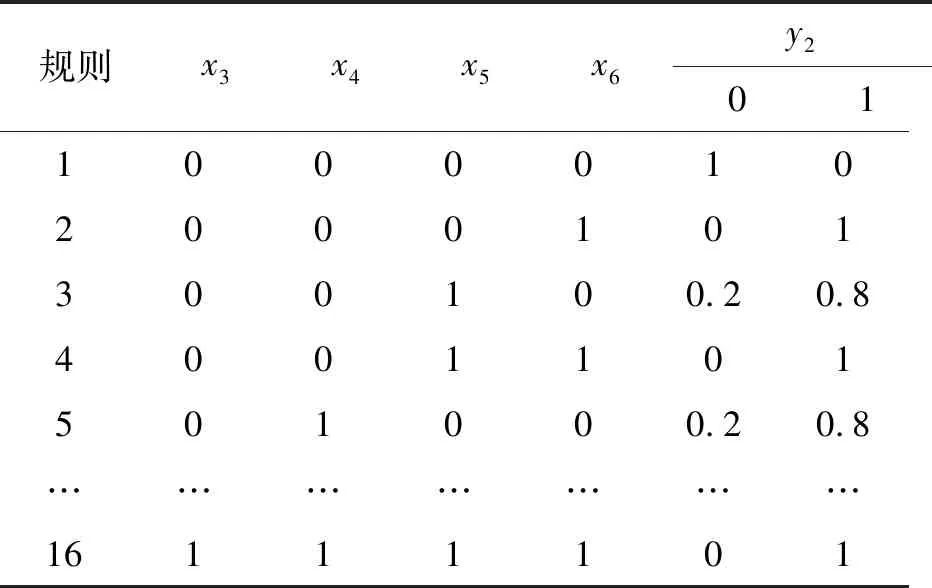
表5 G2门规则
G4门中,任何一个下级事件发生都会引起上级事件发生。G4门规则见表6。

表6 G4门规则
由式(1)—(3),通过表4—6的T-S规则和表3底事件发生概率,求得x1—x11概率重要度见表7。

表7 基本事件概率重要度
3.3 最优故障诊断序列决策
由表3和表7构建决策矩阵Y,再由式(10)得规范化后的决策矩阵Z为
Z=
由式(11)和式(12)确定各属性理想解和负理想解见表8。
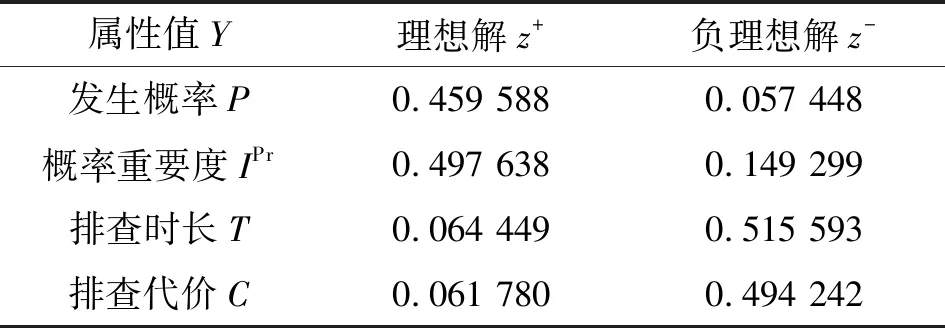
表8 各属性理想解和负理想解
由式(13)和式(14)得基本事件x1—x12到理想解和负理想解的距离见表9。

表9 基本事件到正理想解和负理想解的距离
由式(15)最终得出基本事件xi的综合评价指数Ci如图9所示。

图9 基本事件综合评价指数Ci
由图9可知,正流量液压挖掘机行走跑偏最优诊断序列为:x1,x4,x6,x3,x7,x5,x2,x8,x9,x10,x11。
4 结论
(1)提出了一种基于T-S故障树的故障最优诊断序列多属性决策方法,在具有不确定事件关系、事件多故障状态和不确定事件信息的系统故障诊断中具有极大优势。
(2)研究了正流量液压挖掘机行走液压系统工作原理、主泵变排量控制方法和行走马达结构组成,总结行走跑偏的原因和排查方法,在定位故障源、排查故障方面具有重要参考价值。
(3)将所提基于T-S故障树的故障诊断最优序列多属性决策方法应用于正流量液压挖掘机行走跑偏分析,生成最优诊断序列,在快速精准、最小代价检修故障源方面具有重大指导意义。
