悬垂结构零件多轴增材加工非均匀层填充方法
2023-10-07耿聪耿大鹏王金杰
耿聪,耿大鹏,王金杰
(沈阳建筑大学机械工程学院,辽宁沈阳 110168)
0 前言
悬垂结构零件具有底部悬空无支撑的几何特点,近年来广泛应用于复杂零件的设计中。增材制造可加工成型任意形状的零件,是实现复杂形状零件加工的有效途径[1-4]。
根据各层厚度是否相同,可将现有算法分为等厚度填充算法和自适应填充算法2类。采用等厚度填充算法所得到的各层厚度相同,算法实现较为简单[5]。但是,当零件表面曲率变化较大时,使用等厚度填充算法得到的零件表面精度较差。为克服这一不足,自适应填充算法根据零件表面曲率、成型几何误差(弦长、体积偏差等)调整各层厚度,得到满足精度要求的分层[6-9]。
采用三轴混合机床加工悬垂结构零件时,由于加工方向固定,需要添加若干支撑结构[10-11]。这种方式不可避免地会降低整体加工效率,带来原材料浪费。多轴混合机床在三轴机床结构基础上增加了旋转轴,可实现无支撑结构的增材加工。国内外学者对多轴增材加工方法展开了深入研究。ZHANG、LIOU[12]提出了一种适用于多轴增材加工的自适应分层方法,可根据零件表面法向量调整加工方向,实现零件的自适应填充。XIAO、JOSHI[13]开发了一种适用于五轴增材加工的自动规划软件,该软件可自动将零件划分为多个加工序列进行成型制造。LEE、JEE[14]将零件分解为主体和悬垂部分,在完成主体部分加工后,改变加工方向完成对悬垂部分的加工。上述文献均将悬垂部分单独分离,在完成非悬垂部分加工后,再加工悬垂部分,影响整体加工效率。针对这一问题,RUAN等[15]提出将悬垂结构零件作为一个整体进行区域划分,而后在各个区域采用单层均匀层厚堆叠,最后减材加工形成非均匀层。这种先增材加工而后铣削加工出非均匀层的方法,不仅增加了加工时间,也带来了材料的浪费。
针对上述问题,本文作者以熔融沉积成型(Fused Deposition Modelling,FDM)为制造工艺,提出一种适用于悬垂结构零件多轴增材加工非均匀层填充算法。与现有方法先增材再减材加工出非均匀层的思路不同,文中方法首先限定阶梯误差最小,确定各层最大层厚、最小层厚和成型角度,进而求解单层填充轮廓,并通过调整增材填充速率,直接形成非均匀厚度层,实现对具有悬垂结构零件的无支撑快速加工,提升整体加工效率。
1 多轴非均匀层成型方法
如图1所示,悬垂结构零件具有底部悬空无支撑的几何特点。加工该结构增材时,若原材料成型方向无法改变,则需要构造支撑,影响加工效率和原材料利用率。多轴混合加工机床的刀具在3个平移轴基础上,增加了旋转轴,使该类零件的无支撑结构加工成为可能。

图1 悬垂结构零件示意
文中结合悬垂零件的结构特点,提出适用于悬垂结构零件多轴增材加工非均匀层填充方法。该方法在满足填充层厚限制的条件下,确定单层两端层厚d1、d2与成型变化角度θ的变化范围,在保证填充各层阶梯误差最小的条件下,实现零件的非均匀层填充。算法包括以下4个步骤:(1)读取模型轮廓数据,建立平面直角坐标系,完成轮廓点坐标由空间直角坐标系到平面坐标系的转换;(2)在阶梯误差最小的情况下,确定单层两侧层厚和成型变化角度;(3)根据两侧层厚与成型变化角度,确定填充轮廓上各点坐标;(4)通过调整增材填充速率,直接形成非均匀厚度层。下面将分别介绍各部分具体实现过程。
1.1 零件轮廓的确定
如图2所示,使用三维建模软件获取模型数据轮廓s,满足曲面方程:
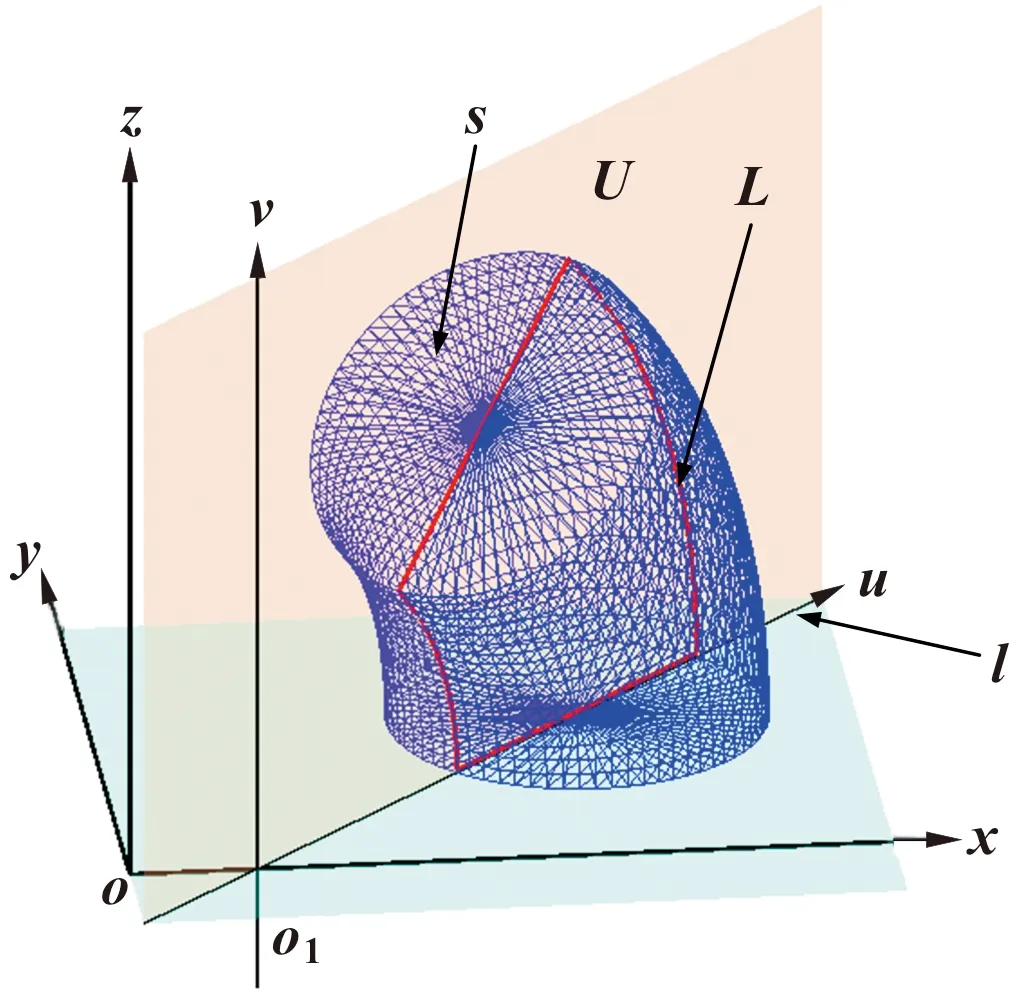
图2 空间直角坐标系oxyz中的待加工零件
s(x,y,z)=0
(1)
平面U在空间直角坐标系oxyz内垂直平面xy,满足:
ax+by+c=0
(2)
则零件数据轮廓s与平面U相交所得截面满足:
z=g(x)
(3)
为使零件数据轮廓s与平面U相交得到的截面轮廓面积L最大,即:
(4)
令其关于自变量a、b、c偏导值为零,可确定平面U的表达式。
(5)
如图2所示,若平面U与xy平面相交于直线l,该直线与x轴相交于点o1(-c/a,0,0),以点o1为原点,以直线l的单位方向向量为横轴u,过点o1取与z轴平行的单位向量为v轴,建立右手笛卡尔平面直角坐标系uo1v:
(6)
空间直角坐标系oxyz中任意点P(xp,yp,zp)在所建立的平面直角坐标系uo1v中的点坐标可表示为P(up,vp),满足:
(7)
1.2 基于最小阶梯误差的多轴非均匀层填充
在建立平面直角坐标系后,零件轮廓点坐标就由空间直角坐标系转换到平面坐标系中表示。接下来,将在填充阶梯误差最小的前提下,计算单层两侧层厚和成型变化角度,确定各层填充轮廓,并通过调整填充过程中喷嘴的进料速度,实现多轴非均匀层的填充加工。
1.2.1 层厚和成型角度确定
在取得任意零件曲面在平面坐标系中的二维截面轮廓后,此算法采用若干直角梯形近似逼近该截面轮廓。
如图3所示,连接两端点A(ua,va)和点B(ub,vb),作AB垂直平分线与BC延长线交于点E(ue,ve),其满足:

图3 平面直角坐标系uo1v中对应截面
(8)
如图4所示,过点E作斜率为ki(i=1,2,…,n)的直线li,与截面轮廓交于点Pi4和Pi6,可将截面分为n层。过直线li-1上的点P(i-1)6作P(i-1)6Pi3垂直直线li于点Pi3,过直线li上的点Pi4作Pi4Pi1垂直直线li-1于点Pi1。点P(i-1)6与点Pi2重合,点P(i-1)4与点Pi5重合,在最底层中,点P(i-1)6与点C重合,点P(i-1)5与点B重合。以此构造出直角梯形Pi1Pi2Pi3Pi4近似逼近各层形状。在第i层直角梯形中,上底边Pi2Pi3和下底边Pi1Pi4的长度分别为该层填充的最小层厚di2和最大层厚di1,上底边对应的钝角∠Pi1Pi2Pi3为此层法向量与上一加工平面切向量的夹角。
采用直角梯形层层堆叠形成加工零件轮廓时,加工层与零件在边缘处存在一定偏差,这种偏差称为阶梯误差。如图4所示,当采用实线所示直角梯形Pi1Pi2Pi3Pi4对虚线所示零件第i层进行填充时,由于填充单层层厚较小,该层阶梯误差近似于两侧三角形面积和Si:
Si=SΔPi2Pi3Pi6+SΔPi1Pi4Pi5=
(9)
该轮廓填充的总阶梯误差S表示为各层阶梯误差的总和:
(10)
在满足层厚限制的条件下,使阶梯误差最小,加工零件各层最小层厚di2、最大层厚di1与成型角度θi的数学模型表示为
其中:dmin、dmax和θmax分别对单层堆叠的最小层厚、最大层厚和最大成型角度;θs为成型总变化角,满足:
(11)
求解式(11)可确定填充阶梯误差最小条件下各层两侧层厚di2、di1和成型角度θi。
1.2.2 单层填充轮廓的确定
在得到填充阶梯误差最小条件下的各层两侧层厚di2、di1和成型角度θi后,任意层的填充轮廓就可以确定。如图5所示,任意第i层填充轮廓为由li1、li2、li3、li44条边组成的直角梯形,Pi2、Pi6、Pi4、Pi5围成虚线为该层零件截面,∠Pi1Pi2Pi3为直线li1与直线li4相交所成的钝角,满足:

图5 第i层直角梯形逼近截面表示
∠Pi1Pi2Pi3=θi+90°
(12)
在第i层直角梯形中,确定各点坐标Pi1(ui1,vi1)、Pi2(ui2,vi2)、Pi3(ui3,vi3)、Pi4(ui4,vi4)、Pi5(ui5,vi5)和Pi6(ui6,vi6),即可确定该层轮廓。对于底层直角梯形,点P15(B)和点P12(C)为零件轮廓与U轴的2个交点,可通过计算得到;对于其余各层,第i层的Pi2、Pi5分别与i-1层的Pi6、Pi4重合。因此,点Pi2和点Pi5为已知量,只需求解其他4点Pi1、Pi3、Pi4、Pi6。下文将详细介绍这4点坐标的求解过程。
通过上一步骤确定各层层厚和成型角度后,由于Pi3与Pi2相距di2,且∠Pi1Pi2Pi3已知,可通过式(13)确定Pi3(ui3,vi3):
(13)
直线li2过Pi3(ui3,vi3),且与直线li1垂直,则其表达式为
(14)
确定直线li2表达式后,则可得到跟零件轮廓S相交两点Pi6和Pi4的坐标值。又由于点Pi1和点Pi4距离是di1,且Pi1Pi4平行于Pi2Pi3,可通过式(15)确定Pi1的坐标值:
(15)
通过上述步骤,可确定第i层直角梯形中所有点坐标,进而确定该层填充轮廓。
1.2.3 填充速率的确定
在增材填充加工过程中,单层填充层厚d满足:
(16)
其中:r为喷嘴半径;f为喷嘴进料速度;v为机器移动速度;k为轨迹宽度。对于特定机床,其喷嘴半径r和轨迹宽度k恒定不变。在实际填充中,保持机器移动速度v不变,单层填充层厚d与喷嘴进料速度f成正比,通过改变喷嘴进料速率即可实现不同层厚的加工。
如图6所示,增材填充单层时,加工平面由多条填充轨迹组成。每一条填充轨迹的厚度均匀,相邻填充轨迹的厚度逐步增大,满足线性关系。路径加工的截面如图7所示。
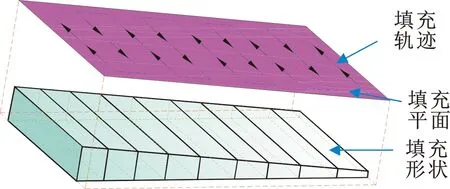
图6 单层加工面填充轨迹与填充结果

图7 第i层加工轨迹填充截面
在进行非均匀层填充时,每条轨迹所填充的截面面积Aip可由式(17)确定。
(17)

结合式(16)与式(17),可得出喷嘴在加工轨迹上的进料速率f的表达式:
(18)
2 实验验证
为验证文中所提出算法的有效性,对图8所示零件进行实验验证。该零件是一段半径为R=45 mm、弧度为π/2的圆弧,其截面为10 mm×10 mm的正方形。设定多轴增材加工机床的喷嘴可填充最小层厚0.5 mm,最大层厚1.0 mm。

图8 目标加工零件
图9所示为等厚度填充仿真效果。图10所示是根据曲率变化对零件进行自适应填充的仿真效果,可以看出:各层厚度在0.5~1.0 mm内变化。与等厚度填充法相比,自适应填充算法得到的各层厚度不同,但两方法在填充单层时的厚度均保持不变。图11所示为采用文中方法对零件进行非均匀填充的仿真效果。图中相同颜色部分的堆叠厚度相同,同层填充厚度在0.5~0.625 mm内变化。与等厚度和自适应填充方法不同,采用文中方法填充,单层厚度也会发生变化。

图9 等厚度算法分层仿真结果

图10 自适应算法分层仿真结果

图11 文中方法分层仿真结果
效率和精度是评价算法效果的两个重要指标,两者与填充层数和填充层阶梯误差的大小有关,层数越多,效率越低,各层阶梯误差越小,增材填充精度越高。表1所示为分别采用等厚度填充算法、自适应填充算法和此算法对图8所示零件加工,在层数、填充面积与阶梯误差间的差异。可知:在满足喷嘴最大加工层厚的情况下,文中方法与等厚度填充算法得到的层数分别为79和70,远小于自适应填充算法得到的层数92。

表1 不同分层方式参数与实验数据对比
设定机床的喷嘴可填充最小层厚0.5 mm,最大层厚1.0 mm,在得到分层信息后,采用Vericut中的beam_magic2机床进行仿真加工,喷嘴加工宽度为1 mm,移动速度为80 mm/s,增材仿真加工的结果如图12所示。

图12 零件填充加工
在增材填充过程中,层数与效率成反比,层数越多,待填充加工面积越大,其效率越低,加工数据如表1所示。采用文中方法加工,其填充面积为7 900 mm2,与等厚度填充算法面积(6 969 mm2)相近,远小于采用自适应填充算法进行填充的加工面积(9 086 mm2)。这意味着在该零件的加工中,采用文中方法和等厚度填充算法能够得到较高的加工效率。
采用等厚度填充算法对该零件进行实验加工时,形成的阶梯误差为7.206 1 mm2,远大于文中方法填充阶梯误差0.647 9 mm2。为提升等厚度填充算法加工精度,一般采用增加等厚度填充层数的方法。在将分层层数增至140,加工层厚限定至最小值0.5 mm后,填充阶梯误差由7.206 1 mm2缩小到3.632 1 mm2,但填充面积由6 969 mm2增至14 036 mm2,大大降低了加工效率。而当文中算法加工层厚取最小值时,误差可达到最小值0.252 3 mm2,不仅优于等厚度填充算法和自适应填充算法,而且还优于文中加工层厚取最大值时的误差。文中加工层厚取最小值时,填充面积由7 900 mm2增至12 600 mm2,会降低加工效率、提高加工精度。
采用文中方法进行实际加工,填充加工材料为PLA,加工出的零件如图13所示。

图13 加工零件
综上所述,相较于等厚度填充、自适应填充等均匀层厚填充方法,在满足填充层厚的条件下,采用文中方法对零件进行加工,可获得更好的加工效率和加工精度。
3 结论
文中提出一种针对具有悬垂特征零件的多轴增材加工非均匀层填充算法。该方法将模型轮廓三维点坐标转换为平面直角坐标系中的二维点表示,在保证阶梯误差最小的情况下,确定各层两侧层厚和堆叠角度,进而得到填充轮廓上各点坐标。实验结果表明:与传统等厚度填充和自适应填充方法相比,文中方法采用一系列非均匀层完成零件的填充加工,该过程无需支撑结构,且与传统均匀层填充方法相比,文中方法能够达到更高的加工效率与加工精度。文中方法同样适用于曲率变化大零件的增材填充。
