基于自适应降阶滑模算法的受约束多机械臂力/位混合控制
2023-10-07朱志浩李蔚高直郭毓
朱志浩,李蔚,高直,郭毓
(1.盐城工学院电气工程学院,江苏盐城 224051;2.盐城工学院信息工程学院,江苏盐城 224051;3.南京理工大学自动化学院,江苏南京 210094 )
0 前言
近年来,随着我国工业的快速发展,机器人的应用得到了极大的发展,并逐步运用到了制造业、农业等领域。同时国内对于机器人的研究也逐年深入,但这些应用和研究大多集中于单机械臂领域[1-2],对于多机械臂[3]的研究和应用仍有所缺乏。在实际应用方面,单机械臂有着效率低下、易受干扰、无法适应复杂的工作环境、面对大而重的物体力不从心等诸多局限性,因此相较于单机械臂系统,多机械臂系统有很大的优势。
虽然相比于单机械臂系统,多机械臂在实际运用中有着诸多的优势,但这也对其提出了更高的控制要求。当多机械臂控制物体在约束环境上运动时,多机械臂与物体形成一个整体,所以不仅要考虑控制物体按照期望的位置指令运动,控制物体与约束环境间约束力,还需要考虑控制机械臂对于物体的夹持内力[4],保证机械臂稳固控制物体的同时不对物体造成损伤。因此,针对多机械臂系统的力/位混合控制问题[5-8],国内外专家们提出了诸多的控制方法。文献[9-13]将命令滤波与反步法相结合,同时基于误差补偿系统来消除滤波误差。文献[14]设计了一种滑模控制算法,解决了协调机械臂不确定性问题。文献[15]设计了一种神经网络自适应算法,克服模型建模以及时间滞后对系统的影响。然而这些方法控制器的设计都比较复杂,并且只单独考虑位置和内力的问题,忽略了约束力的影响。本文作者提出一种基于自适应降阶滑模算法的受约束多机械臂力/位混合控制方法,首先将位置控制、约束力控制、内力控制引入同一控制器;其次设计自适应律补偿未知扰动提高控制精度,利用降阶方法提高响应速度;最终经过李雅普诺夫方法,证明系统的稳定性,并经过仿真证明控制策略的有效性。
1 问题描述
建立由k个n自由度机械臂及被控物体所组成的多机械臂系统。多机械臂系统坐标系由三部分组成,如图1所示:任务空间坐标系{O},以物体的重心为原点的坐标系{G},以机械臂末端执行器为原点的坐标系{Ei}(1≤i≤k)。为方便研究,满足如下几点假设[16]:

图1 多机械臂系统
假设1,每个机械臂自由度相同;
假设2,被控物体为刚性物体;
假设3,整个系统为非冗余的;
假设4,所有转换矩阵均满秩且有界。
1.1 多机械臂动力学模型
第i个机械臂动力学模型[17]为
(i=1,2,…,k)
(1)
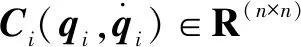
由式(1)可得k个机械臂所组成的多机械臂动力学模型:
(2)
其中:
D(q)=blockdiag[D1(q1),D2(q2),…,Dk(qk)]∈Rkn×kn;
Je=blockdiag[Je1,Je2,…,Jek]∈Rkn×kn;
式(2)所描述的动力学模型具有如下性质:
性质1:存在正数k1、k2,满足下式:
(3)

(4)
性质3:存在参数线性化关系:
(5)
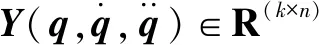
1.2 被控物体动力学模型
被控物体的动力学方程为
(6)

(7)
其中:Joi(x)∈Rn×n为从机械臂末端位置向量到x的Jacobian矩阵;Fei∈Rn为机械臂末端对物体的力。Fe可分为内力FI∈Rk×n和外力Fo∈Rk×n两部分。

由式(7)可得:
(8)
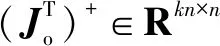
1.3 多机械臂系统动力学模型

xe=φ(q)
(9)
其中:φ(q)∈Rn×n为从q到位置向量xe的变换矩阵。
对式(9)左右同时求关于时间的导数,得:
(10)
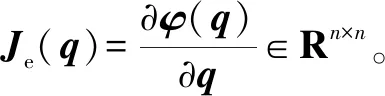
又有:
(11)
其中:Jo(x)∈Rn×n。
由式(10)(11)可推导出:
由假设4可知Je可逆,则有:
(12)
对式(12)左右同时求关于时间的导数,得:
(13)
把式(12)(13)(8)(6)代入式(2),可得:
(14)

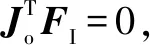
(15)
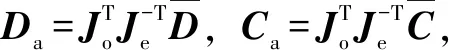
式(15)描述的动力学方程具备与式(2)相似的性质。
1.4 受约束多机械臂系统动力学模型
设多机械臂系统在m维约束环境运行。取xc为物体与约束面的接触点,则对于物体重心位置向量x,有xc=h(x),因此约束环境可表示为
ψ(x)=Φ(h(x))=Φ(xc)=0
(16)
由式(16)左右两边同时关于时间t求导得:
(17)
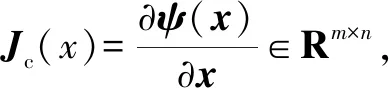
由式(6)可得受约束物体得动力学方程为
(18)
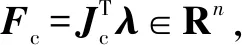

(19)
(20)
(21)
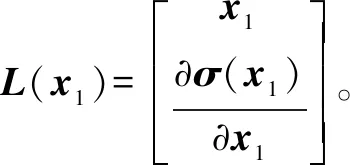
将式(20)(21)代入式(19),得:
τa+Fc
(22)
则受约束多机械臂系统动力学方程表示为
(23)
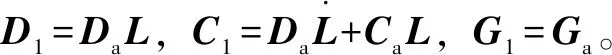
式(23)所描述的动力学模型具有如下性质:
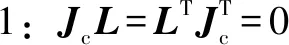
性质2:具备与式(2)性质3相似的性质,即满足参数线性化关系。
将式(23)两边同左乘LT(x1),推导可得:
(24)

2 控制器设计
设xd为期望的物体重心位置向量,定义以下变量:
(25)
其中:x1e为位置误差;x1d为x1的期望位置;x1r为系统误差向量;Λ>0。
滑模函数为
(26)
力误差:
eλ=λ-λd
(27)
其中:λd为期望接触力。
设计控制器为
(28)

由式(23)及其参数线性化关系可得:
(29)
其中:Ya为回归矩阵;Pa为系统未知定常向量。
用于控制力的项:
λr=λd-Kλeλ
(30)
则可得位置和力的控制器为
(31)

(32)

设计如下李雅普诺夫函数为

对等号两边关于时间t求导得:

(33)
式中:λmin为矩阵LTL的最小特征值。

为了使得机械臂有效控制物体,则在受约束多机械臂系统控制器中加入内力控制,与式(14)相似,将式(12)(13)(8)(18)(20)(21)代入式(2)得:
(34)
其中:
CoL
设用于控制内力的项为
CoL
CoL
FIr=FId-KIeFI
其中:KI>0;eFI=FI-FId,FId为期望内力。

(35)
则最终的受约束多机械臂系统控制器为
(36)
3 仿真分析
针对受约束双二自由度机械臂系统模型进行仿真验证,进而证明文中所设计控制方案的有效性。受约束双二自由度机械臂系统模型如图2所示。

图2 受约束双机械臂模型
其机械臂的动力学模型参数如下:
Ci(qi)=
Gi(qi)=
Jei(qi)=
物体的动力学模型参数如下:
取参数:
控制器参数如下:
li1=li2=1.0 m,mi1=mi2=1.0 kg,mo=2.0 kg,
g=9.8 m/s2,R=0.2 m,
x1d(0)=0.6,x2d(0)=1.117 2,
x1(t)=0.8+0.1cost,
FId1=FId2=7 N,FId3=FId4=-7 N,
Λ=11I2,Kd=25I2,w=2I2,
Kλ=10,KI=7I2,Γ=7I2。
仿真结果如图3—6所示。由图3可以看出:与未改进的多机械臂自适应位置控制相比,文中所使用的基于自适应降阶滑模的力/位混合控制算法能够有效提高控制器的控制精度和系统的响应速度;在位置指令跟踪上,文中所使用的方法虽然在起初有较大波动,但很快便在1.6 s时跟踪上,而反观对比方法在2.4 s才跟踪上,响应速度有了显著提升,并且对比方法在之后的跟踪过程中仍有一定的波动产生,而所设计控制方案就能够很好地贴合期望轨迹。从图4—6来看,所设计的控制方案的约束力误差、内力误差虽然起初有一定的波动,但很快趋于平稳,且将误差限定在极小的范围内,说明了所设计控制器的有效性。
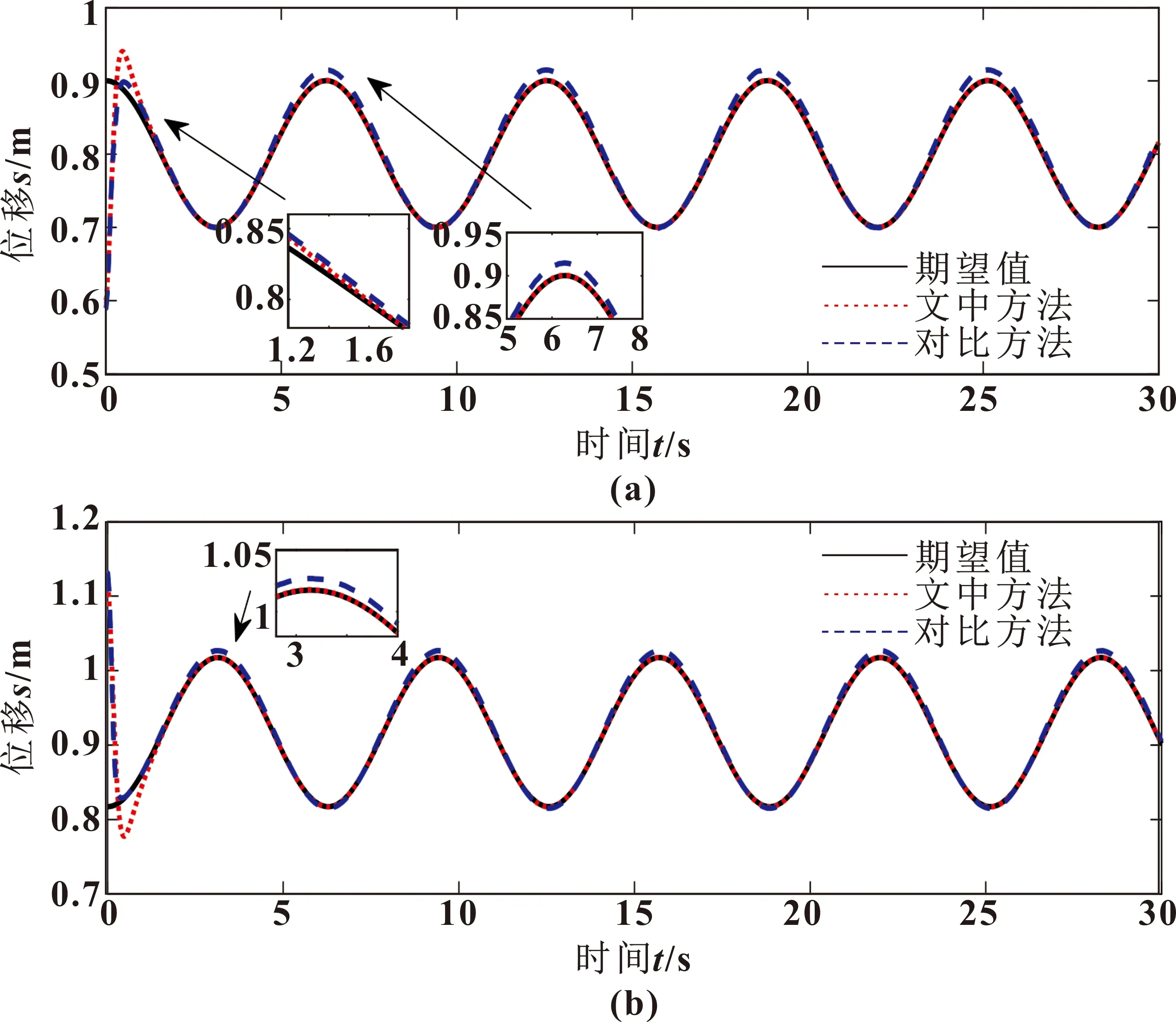
图3 位置跟踪

图4 约束力跟踪误差

图5 机械臂1内力误差
4 结束语
针对受约束多机械臂系统模型,将自适应滑模算法与降阶方法相结合,实现了受约束多机械臂的力/位混合控制。仿真结果表明:所设计的控制方案能够有效提高控制器的控制精度和系统的响应速度,且多机械臂系统的内力和约束力可以限定在理想的范围内,验证了控制方案的有效性。
