具有不确定性的主从机械手自适应模糊控制
2023-10-07李超凡王福杰余元佳郭芳任斌樊开夫
李超凡,王福杰,余元佳,郭芳,任斌,樊开夫
(1.东莞理工学院电子工程与智能化学院,广东东莞 523000;2.东莞理工学院国际微电子学院,广东东莞 523000;3.东莞松山湖材料实验室,广东东莞 523000)
0 前言
近年来,机器人遥操作系统在深海探测控制、太空遥操作、手术微操作、医学内脏健康检查等场景展示了强大的潜在应用前景[1-2]。基于机器人遥操作系统的自适应控制成为目前研究的核心问题,也吸引了众多的学者研究该类控制问题[3-5]。文献[3]基于主从机器人动力学模型设计非线性类PD控制器,通过进行机器人重力补偿同时实现主从机器人关节角度与速度误差收敛。文献[6]基于主从机器人的任务操作空间提出一种异构机器人同步算法,并利用机器人冗余空间完成避障任务,取得良好的控制效果。
机器人系统是一个多输入、多输出、强时变耦合的非线性系统[7-8],在实际生产中的序列任务,机器人系统和环境的交互模型一般是难以精确实时标定的,受限于不断变化的负载(包括体积、质量、摩擦等)[7-12],引发了机器人系统的动力学、运动学与执行器不确定性。在机器人模型不确定与执行器受约束情况下完成复杂的精确控制,是目前研究的难点。文献[13]提出一种将PID与鲁棒自适应相结合的遥操作机器人控制算法,通过动力学模型“参数线性化”方法处理主从端动力学不确定性问题,确保主从机器人的位置与速度误差在时延网络下依然收敛于0。由于机器人雅可比矩阵对物理参数的要求,现在已经有学者提出了几种自适应控制算法来处理运动学不确定性[14-15]。如文献[11]设计基于滑模函数的鲁棒自适应控制律补偿机械手模型不确定性,利用自适应律估计外界干扰的上界。基于上述处理思路,文献[4]针对不确定与受干扰遥操作机器人系统提出一种滑模鲁棒控制器,通过设计速度观测器避免噪声速度信号的采集,在控制律中嵌入指数控制项加快误差的收敛速度。文献[16]开发了一种半自主控制框架,同时考虑机器人运动学与动力学的不确定性,利用异构机器人来提高复杂环境下运行的远程操作系统的运行速度。上述控制方案都基于精确的动力学结构而只考虑参数的不确定性进行研究的,在复杂多变的实际环境下这种要求难以实现。此外,上述文献假设机器人执行器处于完备运行状态中,文献[17]指出当机器人长期处于运行状态,执行器无法避免产生输入约束,使实际的关节力矩给定值与输出值形成非线性映射,因此上述控制算法在许多任务中难以完美实施。
本文作者针对一类具有动力学模型、运动学参数不确定和执行器未知特点的机器人遥操作系统,利用模糊系统对非线性函数的逼近能力与动力学模型进行预估,避免文献[9-12]中对机器人动力学模型 “回归矩阵”的求解,将关节空间的域误差变量以及任务空间的误差变量引入到控制律中进行反馈,通过在控制律中嵌入Nussbaum增益函数实现对执行器不确定性的补偿,增加了轨迹跟踪误差的收敛速度,确保稳定性和任务空间位置跟踪。此外,文中的控制方案也引入投影函数[11]避免 “奇异”现象,在控制器中设计鲁棒项进行扰动抑制,避免求解未建模动态与外部扰动的上确界,因此文中提出的控制方案能减少计算复杂度。在进行主从机器人系统交互控制器设计中,利用自适应模糊控制器的逼近特性,设计带有自适应项的控制律对机械手末端的相互作用力进行补偿,提高了控制算法的实用性。
1 具有输入约束的不确定主从机器人系统
1.1 主从机器人系统运动学
在远程操作系统中,假定双边操纵器(即本地机器人和远程机器人)是非冗余的,机械手的正向运动学[4]可以表示如下:
(1)
主从机器人之间的跟踪误差[5-7]可以定义为
(2)

特性1:机器人的运动学在一组运动学参数θk,i∈Rn×m中是线性的。
Ji(qi)ξ=Yk,i(qi,ξ)θk,i
(3)
其中:Yk,i(qi,ξ)∈Rn×n表示回归矩阵;ξ∈Rn是可微的矢量。文中假设存在运行学不确定性,则Ji(qi)是未知的。
1.2 具有输入约束的主从机器人系统动力学
此外,文中考虑了机器人执行器不确定性。在不失一般性的前提下,假设主机器人和从机器人是具有相同距离的机器人操纵器,遥操作机器人的动力学[4,12]可以写成:
(4)

特性2:对称惯性矩阵Mi(qi)是一致正定的。
(5)
其中:β∈Rn×1是任意向量。
1.3 Nussbaum增益函数
当任意偶函数N(χ)满足:
(6)
则任何偶数函数N(χ)都被称为Nussbaum函数。其中,κ0是κ的初始值。文中使用的Nussbaum型函数N(χ)=χ2cos(χ)。至此,有以下引理[17]:
(7)
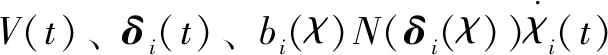
1.4 模糊逻辑系统
典型的模糊系统由4个部分组成,分别是模糊化输入接口、模糊规则库、模糊逻辑推理机以及解模糊化输出接口。而模糊推理机作为整个模糊控制系统的核心部分,通过一套“IF-THEN”规则完成从输入语言变量到输出语言变量的映射。
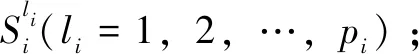


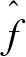
(8)
其中:μAili(xi)为xi的隶属函数,文中采用的隶属函数为高斯基函数。

(9)

(10)
若所有的模糊隶属度函数均为高斯函数,则有以下引理[19]:
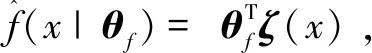
(11)
2 基于不确定主从机器人系统的自适应模糊控制器设计与稳定性分析
2.1 控制器的设计

主从机器人的虚拟控制律设计为
(12)
其中:KD=diag(ki),ki>0,i=1,2,…,n。
(13)
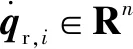
(14)
定义关节空间域参考误差:
(15)
任务空间滑动向量定义为
(16)
具有输入补偿的机器人运动控制器设计[9,17]为
(17)
其中:χ=[χ1,…,χn]T∈Rn×1表示Nussbaum增益矩阵的输入,且有:
N*(χ)=diag(N(χ1),…,N(χn))
(18)
2.2 未知参数预估和自适应律的设计
未知的运动学参数可在线预估为
(19)
(20)
式(17)使用了参数投影法[14],主要是让参数在指定的范围内更新,从而避免预估的雅可比矩阵产生“奇异”现象,投影函数[14]表示为
(21)
Nussbaum增益矩阵的更新律为
(22)
式中:ε=[ε1,…,εn]T表示正常量向量。
2.3 稳定性的证明
定理1:假设主从机器人系统可由式(1)表示其运动学方程,可由式(4)表示其具有输入约束的动力学方程,那么文中提出的自适应模糊控制方案(12)、(17)以及参数更新律(19)(20)(21)可以令主从机器人系统的误差el与er收敛到0,也即实现:
证明:选取李雅普诺夫函数为
(23)
对上式进行微分可得:
(24)
结合式(4)(5)和(15),整理得:
(25)

(26)
又由于:

(27)
由式(16)可得:
(28)
自适应律设计为
(29)
定义模糊逼近误差为
(30)
设计模糊自适应律:
(31)
将式(2)以及(27)—(31)代入式(26)可得:
(32)
当恰当选择KD时有:
因此,对式(32)在区间[0,t)上积分,则有:
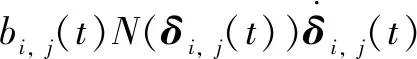
3 仿真结果
为了验证文中提出的具有动力学与运动学不确定性的主从机械手自适应模糊控制方案的有效性,选取带有转动关节的二自由度主从机械手为仿真研究对象。
主从机器人的运动学参数如表1所示,其中li,1、li,2分别表示机器人两个关节的等效杆长,i=r,l,分别指代主机器人与从机器人。由文献[20-21]可知机器人的运动学可以表示为

表1 主从机器人运动学参数 单位:m
主从机器人的动力学参数如表2所示,其中mi,1、mi,2分别表示机器人两个关节质量,ri,1、ri,2分别表示机器人两个关节长度,i=r,l分别指代主机器人与从机器人,则机器人动力学可以表示为

表2 主从机器人动力学参数
式中:
2mi,2ri,1ri,2cos(qi,2)
Gi,1=(mi,1+mi,2)ri,1cos(qi,2)+
mi,2ri,2cos(qi,1+qi,2)
Gi,2=mi,2ri,2cos(qi,1+qi,2)
因此,可得机器人任务空间速度和关节空间速度之间的映射关系可表达为
式中:
Ji,11=-li,1sin(qi,1)-li,2sin(qi,1+qi,2)
Ji,12=-li,2sin(qi,1+qi,2)
Ji,21=li,1cos(qi,1)+li,2cos(qi,1+qi,2)
Ji,22=li,2cos(qi,1+qi,2)
可得式(3)中的回归矩阵可以表示为
式中:
根据上式可以完整得到机器人运动学方程,受限于文章篇幅,机器人动力学参数与具体的模型表达式可以参照文献[21]。控制器和自适应式中的增益分别设置为:KD=3,kr,i=4,ke,i=0.2,λi=1,Γk,i=diag{1,1},Γd,i=[1,1;1,1],εi=diag{1,1},Nussbaum 型函数与模糊逻辑系统的选取可以参照文献[17,19];设定主端机器人、从端机器人的关节角初始值为qr(0)=[1,2]T,ql(0)=[0,0.5]T,速度初始值都为0,时延设定为T=0.05。在t=5 s时对主机器人施加外力Fr=[-50,100]T以及在t=10 s时对从机器人施加外力Fl=[-20,-20]T,其中外力的持续时间均为0.5 s。所提出的控制方案仿真实验结果如图1—4所示。

图2 从机器人位置(a)与速度(b)跟踪误差
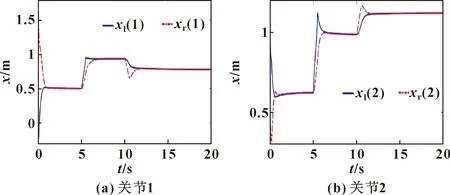
图3 主从机器人位置轨迹跟踪效果
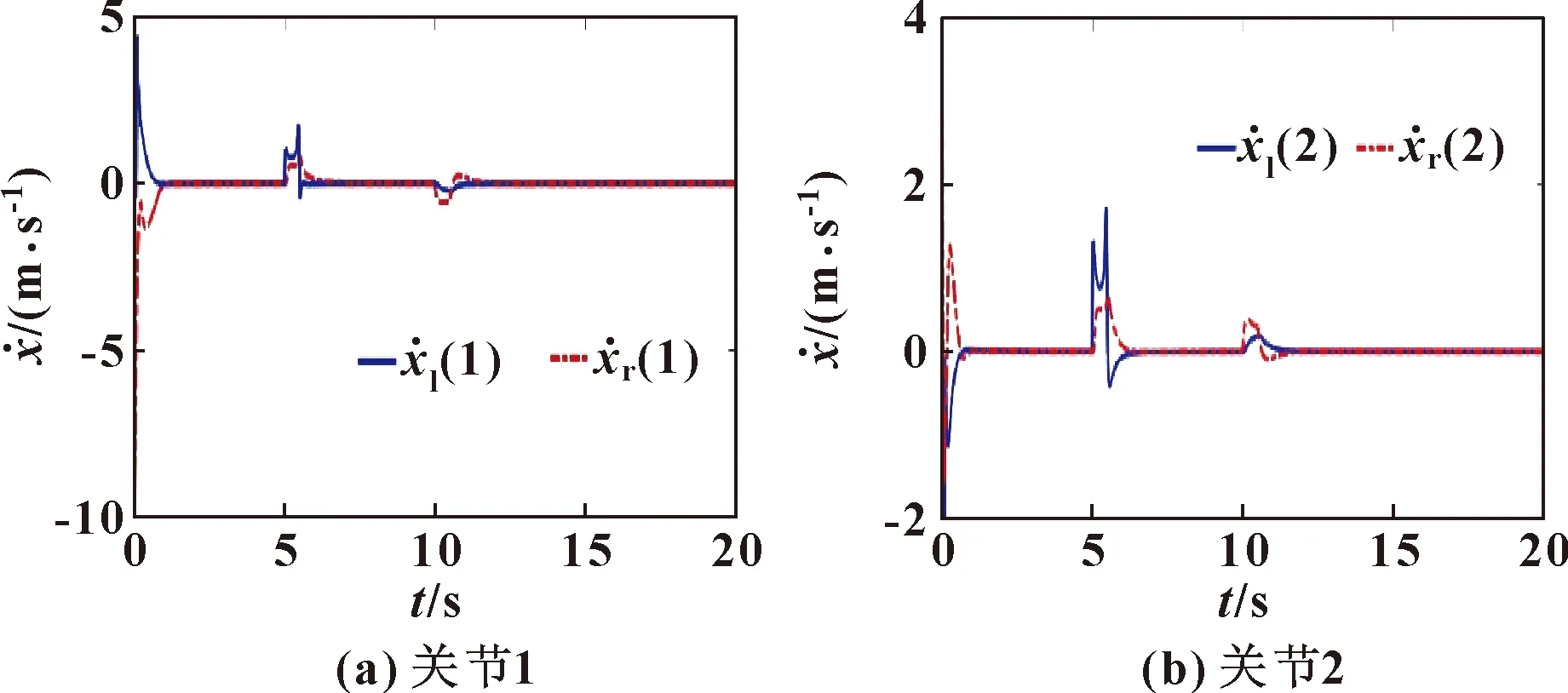
图4 主从机器人速度轨迹跟踪效果
从仿真结果可以看出:所提出的控制方案能够对主从机器人的位置和速度提供良好的同步跟踪性能,证明了控制器的可行性。
4 总结
针对一类存在运动学参数和动力学模型未知特点的主从机器人系统,利用模糊系统的万能逼近特性预估机器人动力学,不需要知道未建模动态以及外部扰动的边界。针对执行器的输入约束,采用了Nussbaum增益矩阵实现对输入约束的补偿。而对于主从机械手存在的一种相互作用力(比如主机械手和操作者之间的摩擦力),提出自适应模糊补偿这种力,使得从机械手能比较稳定而准确地跟踪主机械手的运动路线。
