Numerical Solution of Nonlinear Stochastic Differential Equations by Block Pulse Functions with Improved Operator Matrix

JIANG Guo(姜国),LIU Fugang(刘富钢),CHEN Dan(陈丹)

(School of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

Abstract: This paper introduces an effective numerical method based on the block pulse functions with improved operator matrix to solve the nonlinear stochastic dierential equations.The nonlinear stochastic dierential equation is transformed into a set of algebraic equations by the improved operator matrix of block pulse function.Furthermore,we perform an error analysis and demonstrate that the method converges faster.Finally,numerical examples are used to support the method.

Key words: Stochastic dierential equation;Improved operator matrix;Block pulse function

1.Introduction

Theoretical foundation of stochastic dierential equations (SDEs) was established in the 1960s.With the rapid development of the theory of stochastic analysis,SDE had been widely used in system science,engineering science and ecological science.However,it is difficult to obtain an exact solution for SDE.It makes sense to discuss numerical solutions to the equations[1-10].

Many authors have contributed in these areas.For instance,Akinbo et al.[11]introduced the main concepts and techniques necessary for those wishing to perform numerical experiments involving SDEs.PEI et al.[12]have discussed the stochastic averaging for SDEs.Kloeden and Platen[13]discussed the numerical solution of SDEs.JIANG and Schaufelberger[14]applied block pulse functions (BPFs) to control systems.Heydari et al.[15]illustrated the accuracy and effectiveness of the generalized hat functions method.SANG et al.[16]proposed an effective numerical method to solve nonlinear stochastic Itô-Volterra integral equations.On the other hand,Maleknejad et al.[17]introduced a method for solving stochastic Volterra integral equations,but the results are not very accurate.Therefore,we use BPFs with improved operator matrix to solve the following general nonlinear SDEs (1.1) or (1.2).The advantage of this method is that the calculation is simpler and the numerical solution is more accurate.

wherev(t) is unknown stochastic processes,v0is the initial value,F1(t,v) andF2(t,v) are known analytic functions,andW(t) is standard Brownian motion.

In Section 2,we consider the properties and definition of the BPFs,and show the improved operator matrix and the stochastic integral operator matrix of the BPFs.In Section 3,the numerical method of the nonlinear integral equation (1.2) is obtained.In Section 4,error analysis is presented.In Section 5,some numerical examples illustrate the method.Section 6 is the conclusion.

2.Preliminary

In this section,the improved operator matrix and the stochastic integral operator matrix of BPFs are introduced.

where DKdiag(K) andK(k1,k2,···,km)T.

An arbitrary functionκ(t)2[0,1) can be expanded by the BPFs as

Similarly,we can expand arbitrary two variables functionu(s,t) defined onL2([0,1)×[0,1)) as follows

whereΛ(s) andΦ(t) arem1andm2dimensional BPFs vectors respectively.Meanwhile,U(upq) is them1×m2block pulse coefficient matrix with

The integral of vectorΛ(t) that is given by (2.4)

where the improved matrix[14]

Lemma 2.1[17]Λ(t) is given by (2.4),then

Square integrable functionv(t) in [0,1) can be expressed as

The proof finished.

3.Numerical Method

We apply (2.7) and (2.9) and some properties of BPFs to solve nonlinear stochastic integral equation (1.2).

Forv(t),v0,F1(t,v(t)) andF2(t,v(t)),we have

And by Lemma 2.2,we assume

whereVis unknown,V0andare known BPFs coefficients vectors.

Now substituting (3.1),(3.2),(3.5) and (3.6) in (1.2),we get

By using (2.7)-(2.9),we can obtain

Finally,by solving the unknown vectorV,we obtain an approximate solution.This paper uses the fsolve function in MATLAB to solve the equation (3.9).

4.Error Analysis

Lemma 4.1[16]Supposev(t)2([0,1)) andem(t)v(t)−vm(t),wherevm(t) is the BPFs expansion ofv(t).Then

Lemma 4.2[16]Supposev(s,t)2([0,1)×[0,1)) andem(s,t)v(s,t)−vm(s,t),wherevm(s,t) is the BPFs expansion ofv(s,t).Then

We considerem(t)v(t)−vm(t),wherevm(t),v0m,F1(sm,vm(s)) andF2(sm,vm(s))respectively aremapproximations of BPFs ofv(t),v0,F1(s,v(s)) andF2(s,v(s)).

The following is the main theorem.

Theorem 4.1Suppose analytic functionsF1(s,v(s)) andF2(s,v(s)) satisfy Lipschitz conditions:

(I)|F1(k1,µ)−F1(k2,α)|≤ρ1|k1−k2|+ρ3|µ−α|,

(II)|F2(k1,µ)−F2(k2,α)|≤ρ2|k1−k2|+ρ4|µ−α|,whereµ,R,ρp>0,p1,···,4 are positive constants andk1,k2[0,1).

ProofFor (4.3),we obtain

by using Lemma 4.1 and Lemma 4.2,we have

wherewp,p1,···,4,are independent nonnegative constants.

The proof is completed.

5.Some Example

In this section,we show some numerical examples.

Example 5.1[13]Consider the nonlinear SDE

the exact solution is

Tab.5.1 When m=32,numerical results of Example 5.1

Tab.5.2 When m=64,numerical results of Example 5.1

Example 5.2[6]Consider the nonlinear SDE

Letv0−3,the simulation results form32 andm64 are severally given in Fig.5.3 and Fig.5.4.These two figs also show that the approximate solution fluctuates around the mean orbit,where the mean solution is obtained by 104trajectories.

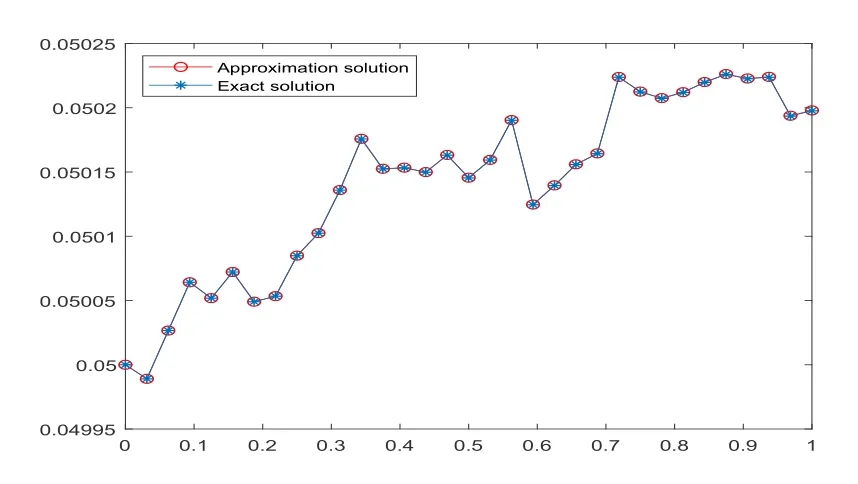
Fig.5.1 When m=32,exact and approximate solutions

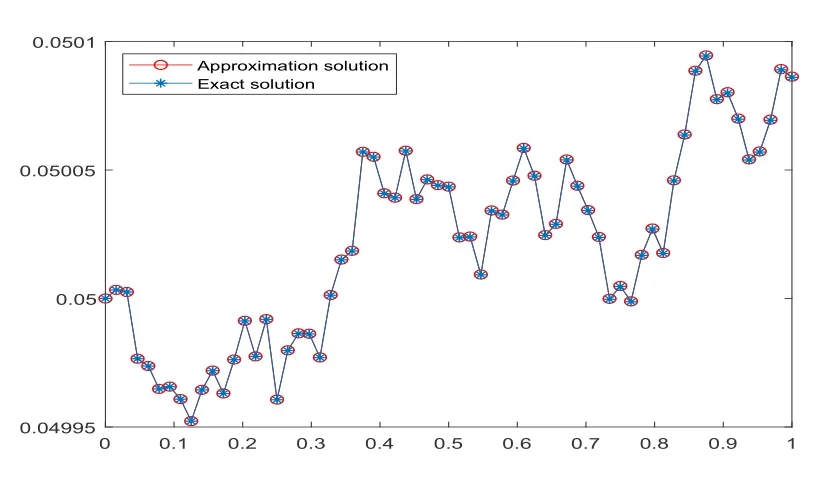
Fig.5.2 When m=64,exact and approximate solutions

Fig.5.3 When m=32,mean and approximate solutions

Fig.5.4 When m=64,mean and approximate solutions

6.Conclusion

This paper proposes a numerical method for solving nonlinear SDEs based on BPFs.By using the improved operator matrix,simulation results show that the solution of this method is very close to the exact solution.Section 4 demonstrates an error analysis and compares it with [2].The method of approximate solution convergence is faster.Some examples are listed to verify the feasibility of the current method.