自旋张量-动量耦合玻色-爱因斯坦凝聚的动力学性质*

邱旭 王林雪 陈光平 胡爱元 文林†

1) (重庆师范大学物理与电子工程学院,重庆 401331)

2) (陕西科技大学物理系,西安 710021)

3) (四川文理学院智能制造产业技术研究院,达州 635000)

利用高斯变分近似及基于Gross-Pitaevskii 方程的数值求解,研究了一维自旋张量-动量耦合玻色-爱因斯坦凝聚中平面波态的动力学性质,发现基态为双轴向列态,其动量随Raman 耦合强度的增加而单调递减.在微扰作用下,基态具有动力学稳定性,且展现出3 种不同的谐振模激发,激发频率与Raman 耦合强度、谐振子势阱的纵横比及相互作用强度有关.通过数值求解变分参数满足的运动方程和Gross-Pitaevskii 方程,发现体系随时间演化将展现出周期性振荡行为.

1 引言

自旋-轨道耦合是粒子的自旋与其运动自由度之间的耦合,在许多新奇量子现象的产生中,起着重要的作用,如量子霍尔效应、拓扑绝缘体[1].通过利用光与原子的相互作用,实验上在电中性的超冷原子气体中实现了人造自旋-轨道耦合效应,如自旋-动量耦合[2-5]、自旋-轨道角动量耦合[6-8].人造自旋-轨道耦合的实验实现,不仅为利用超冷原子系统模拟带电粒子在电磁场中的运动提供了平台,而且也为探索物质场与规范场相互作用所导致的新奇量子现象提供了新机遇.

对于高自旋超冷原子气体(自旋F≥1),除了自旋矢量以外,体系还存在自旋张量,可以用来刻画量子态的向列性和自旋涨落对称性[9].近年来,通过光与原子相互作用,人们发现在高自旋超冷原子气体中还可以实现自旋张量-动量耦合[10,11]和自旋张量-轨道角动量耦合[12],它们是一类新的自旋-轨道耦合效应,其产生的特殊单粒子能带结构使得体系展现出丰富的新奇多体量子态及量子相变,如自旋1 玻色-爱因斯坦凝聚体(BEC)中占据两个不同能带的条纹态[11]和自旋-向列涡旋态[12]、费米原子气体中不同类型的三重简并点[13,14].

到目前为止,关于自旋张量-动量耦合BEC 的研究工作大多聚焦在探索体系可能展现的新奇量子态,仅有部分研究工作分析了自旋张量-动量耦合对吸引原子相互作用BEC 中亮孤子态动力学性质的影响[15,16].本文将结合解析计算和数值模拟,探索一维谐振子势阱中自旋张量-动量耦合BEC 中平面波态的动力学性质.利用高斯函数作为变分计算的试探波函数,首先导出了平面波态的质心坐标、动量、波包宽度、啁啾、相对相位等参数随时间演化所满足的运动方程.通过求解该方程的固定点解及最小化体系的能量泛函,发现基态为双轴向列态,其动量随Raman 耦合强度的增加而单调递减.然后通过对运动方程进行线性化,发现基态在微扰下将保持动力学稳定性,并且展现出3 种不同的谐振模激发,激发频率与Raman 耦合强度、谐振子的纵横比及原子相互作用强度有关.最后,通过数值求解运动方程,发现体系展现出有趣的周期性振荡行为.变分计算结果与基于Gross-Pitaevskii (GP)方程的数值模拟结果相符合.

2 理论模型

设总自旋为F=1、质量为M的87Rb 原子的3 个超精细自旋态分别为 |+1〉,|0〉和 |-1〉.利用3 束波矢为kr、强度为Ωr的Raman 激光去耦合3 个自旋态,其中两束激光沿z方向传播,另外一束激光沿z的反方向传播[10,11].在双光子Raman过程中,原子将在态 |0〉和 |±1〉之间转变,同时发生 2ℏkr动量转移.在旋转波近似下,原子和光相互作用的有效单粒子哈密顿量为[10,11]

在动量空间中,沿z方向的单粒子能量色散关系为

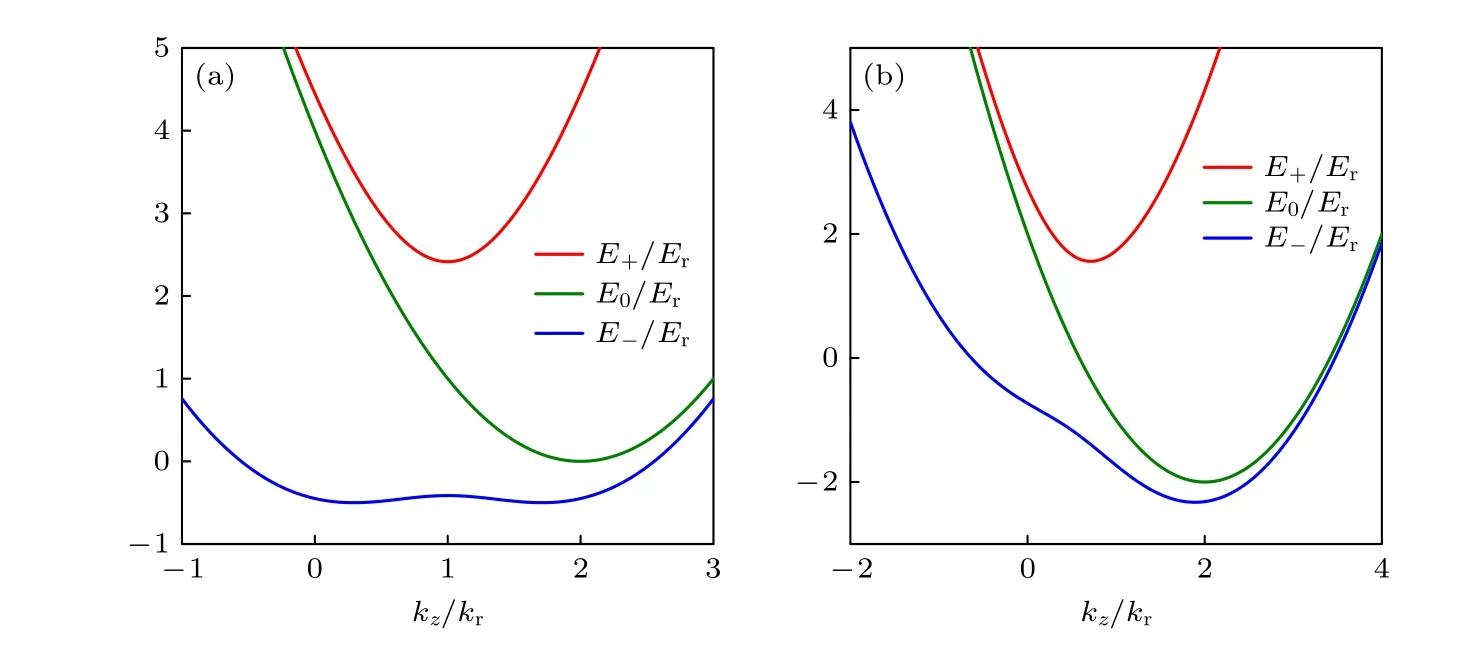
图1 δr/Er=0 (a)和-2 (b)时,单粒子能量色散曲线,其中Ωr/Er=2Fig.1.Single-particle energy dispersion curves for δr/Er=0 (a) and -2 (b),respectively,where Ωr/Er=2 .

由于Ωr,kr和δr在实验中均可调节,本文仅考虑δr=-4Er的情形.在这种情况下,较大的δr使得原子间的自旋混合碰撞过程 2|0〉⇌|+1〉+|-1〉可以忽略[17-21],并且BEC 应为平面波态[11].由于自旋张量-动量耦合沿z方向,因此假设BEC 在xy平面内被频率为ω⊥的各向同性谐振子势阱紧束缚,以至于BEC 在xy平面处于谐振子基态.通过选 择ω⊥和分别作为时间和空间长度的单位,在零温平均场近似下,BEC 沿z方向的动力学性质可用如下的一维GP 方程描述:

其中,ψm(z,t) 代表描述自旋态m=+1,0,-1 动力学性质的凝聚波函数,满足归一化条件分别代表各自旋态的密度和总密度,γ=ωz/ω⊥≪1 代表谐振子势阱的纵横比,ωz为谐振子势阱沿z方向的频率.kR=2krξ⊥和Ω=Ωr/ℏω⊥分别为无量纲化的自旋张量-动量耦合强度和Raman 耦合强度.gn=2N(a0+2a2)/(3ξ⊥) 和gs=2N(a2-a0)/(3ξ⊥)分别为原子间的自旋不依赖和自旋依赖相互作用强度,N为总原子数,a0和a2分别为总自旋为0 和2 的s 波散射通道的散射长度[9].

3 变分计算

通过求解GP 方程(5a)–(5c),可研究体系的基态及动力学性质.然而,由于Raman 耦合、自旋张量-动量耦合和谐振子势阱的存在,很难获得GP 方程的精确解析解.因此,对于弱相互作用体系,本文利用高斯变分法去解析分析体系的基态及动力学性质[25].

描述体系动力学性质的拉格朗日量为

从GP 方程(5a)–(5c)或拉格朗日量(6)可以看出,体系具有交换对称性ψ+1↔ψ-1,因此可以取如下形式的变分波函数去描述平面波态的动力学性质:

其中w代表波函数的宽度,θ与振幅有关,φ和ϕ0代表相位,zc代表波包的质心,k为波矢,c为啁啾,它们都是时间t的函数.则自旋矢量Sx,y,z和向列矩阵N分别为

其中φ=ϕ0-ϕ为相对相位.自旋矢量(8a)表明,由于交换对称性ψ+1↔ψ-1,BEC 在自旋空间中沿着x方向被极化.向列矩阵N的本征值为它们表明: 当Sx=±1 时,体系处于单轴向列态(λ1≠λ2=λ3);当Sx≠±1 时,体系处于双轴向列态(λ1≠λ2≠λ3).

将变分波函数(7)代入拉格朗日量(6)中,并对坐标z积分后可得

由于Nzz=sin2θ,方程(11a),(11b)表明,BEC的质心坐标、动量和自旋张量被耦合在一起,它是自旋张量-动量耦合效应的体现.方程(11c),(11d)说明BEC 宽度的变化将导致相位上出现啁啾[25],而方程(11e),(11f)说明Raman 耦合导致BEC 相对相位和振幅发生耦合.因此,这些参数之间的非线性耦合或将导致BEC 展现出有趣的动力学行为.

4 动力学性质

首先研究基态性质.为了以示区分,用“∗”作为下标去标记基态变分参数.利用能量(10)对变分参数求极值,可得

方程(12)的解实际上也是运动方程(11)的固定点解.图2(a)给出了k∗和θ∗的值,它们随增加而单调递减.图2(b)表明,对于非零的Ω,向列矩阵N的3 个本征值并不相同,说明平面波基态为双轴向列态.图2(c)和图2(d)给出了基态波函数的实部和虚部随空间坐标的变化,表明基态波函数的实部和虚部具有相反的宇称,前者为偶宇称,后者为奇宇称.另外数值求解了虚时演化GP 方程[26],获得了基态的数值解,证实了变分法的计算结果,如图2 所示.

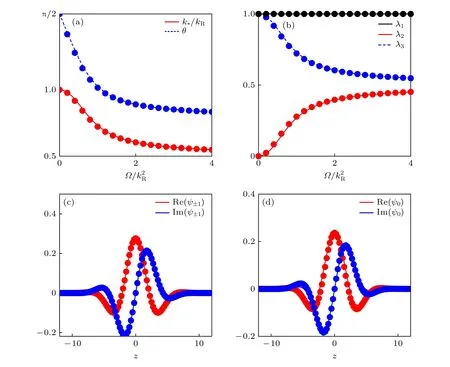
图2 (a),(b)参数 θ∗,k∗ 及向列矩阵 N 的本征值 λ1 ,λ2 和 λ3 随 的变化,其他参数的取值为 gn/kR=1 ,gs/kR=0.1和 =0.2 ;(c),(d)基态波函数的实部和虚部随空间坐标的变化,其他参数的取值为 gn=1 ,gs=0.1 ,γ=0.2,Ω=kR=1;图中的线代表GP 方程的数值解,圆圈代表变分计算结果Fig.2.(a),(b) θ∗ ,k∗ ,λ1 ,λ2 and λ3 as a function of ,where the other parameters are gn/kR=1 ,gs/kR=0.1 and=0.2 ;(c),(d) the real and imaginary parts of the wave functions in ground state for gn=1 ,gs=0.1 ,γ=0.2 andΩ=kR=1.The lines and circles are the results given by GP simulation and the variational method,respectively.

通过线性稳定性分析,接下来研究平面波基态在外界扰动下的动力学稳定性及低能激发性质.设微扰作用下,变分参数为ζ(t)=ζ∗+δζeiωt,其中δζ代表变分参数相对于其基态解ζ∗的偏离,ω为激发频率.将其代入运动方程(11)中,并保留至δζ的一阶项,可得激发频率ω满足的特征值方程

其中

通过对角化方程(13),可获得激发频率ω.图3 给出了ω随的变化.由于体系具有粒子-空穴对称性,6 个不同的激发频率总是正、负成对出现,因此分别标记为ω1,±,ω2,±和ω3,±.图3 显示所有激发频率都是实数,表明各变分参数并不会随时间指数增长或衰减,说明BEC 在微扰下是动力学稳定的.对于较弱的gs和γ,激发频率可近似为

图3 激发频率ω 随 的变化,其中 gn/kR=1,gs/kR=0.1 及=0.1Fig.3.Excitation frequency as the function of ,where gn/kR=1,gs/kR=0.1 and =0.1 .

正如图3 所示,|ω1,±| 随单调递增,但ω2,±和ω3,±保持不变,前者主要由γ决定,而后者与gn有关.因此,在微扰下BEC 将展现出3 种不同的谐振模激发.

最后分析自旋张量-动量耦合BEC 随时间演化的动力学性质.假设t=0 时刻,BEC 的初始动量为0,3 个自旋态的粒子数相等(即且相位、啁啾和质心均为0.通过求解方程(11),图4(a)和图4(b)给出了变分参数随时间演化的性质.可以观察到,BEC 的动量不守恒,其大小随时间周期性变化.同时,在Raman 耦合的作用下,θ也随时间周期性变化,即不同自旋态之间展现出类似于Josephson 或Rabi 振荡行为[27-29],振荡周期与Raman 耦合强度Ω有关.而在谐振子势阱中,BEC 的波包宽度w的周期性变化也导致啁啾c随时间周期性振荡.特别地,从方程(11b)可以看出,BEC 的质心坐标zc与k,θ及c发生耦合,后者的周期性变化导致BEC 的质心坐标也随时间作周期性振荡.此外,以变分波函数(7)作为初始条件,本文也利用时间劈裂傅里叶谱方法数值求解了GP 方程(5)[30],图4(c)和图4(d)给出了各个自旋态的密度随时间的演化,证实了变分计算结果.

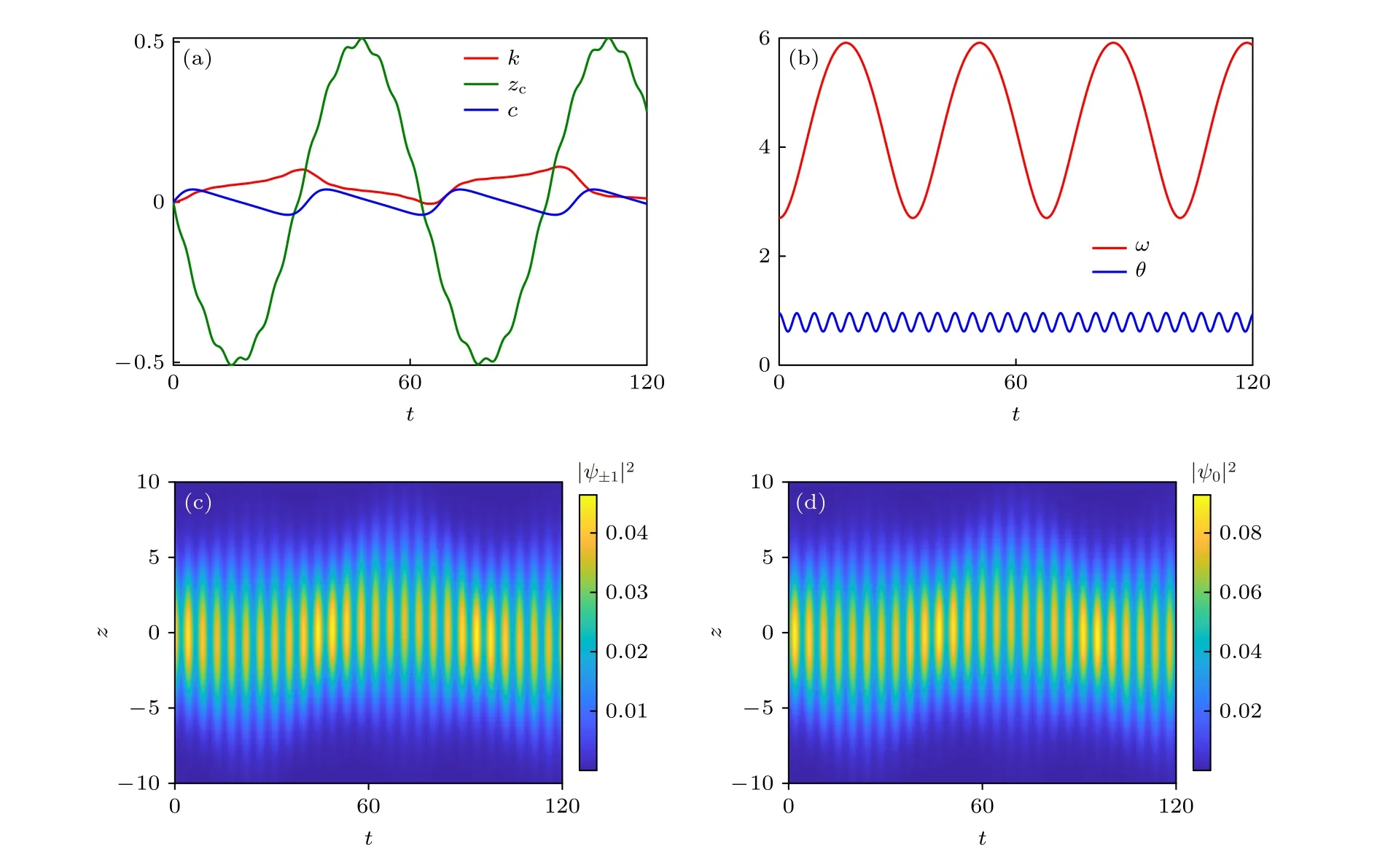
图4 (a),(b)变分参数随时间的演化;(c),(d)各分量的密度随时间的演化(GP 方程的数值解),其中系统参数为 Ω=1,kR=γ=0.1,gn=1 和gs=0.1Fig.4.(a),(b) Evolutions of the variational parameters;(c),(d) evolutions of the densities of each components given by the GP simulation,where the parameters are Ω=1 ,kR=γ=0.1 ,gn=1 and gs=0.1 .

5 结论

本文研究了一维谐振子势阱中自旋张量-动量耦合玻色-爱因斯坦凝聚中平面波态的动力学性质.通过选择高斯函数作为变分试探波函数,导出了变分参数随时间演化所满足的欧拉-拉格朗日方程.利用能量对变分参数求极小值,获得了体系的基态解,发现基态具有非零动量,且基态属于双轴向列态.进一步,基于线性稳定性分析,发现基态在外界扰动下能保持动力学稳定性,并展现出3 种不同的谐振模激发,激发频率与Raman 耦合强度、原子相互作用强度和谐振子势阱的纵横比有关.最终,通过求解含时欧拉-拉格朗日方程,发现动量、质心坐标和波包宽度均随时间周期性变化,体系展现出有趣的动力学行为.GP 方程的数值模拟验证了变分计算结果.