基于深度学习的钻孔辐射压离子加速建模*
2023-10-06张普渡王伟权李哲民张资旋王叶晨周泓宇银燕
张普渡 王伟权† 李哲民 张资旋 王叶晨 周泓宇 银燕‡
1) (国防科技大学理学院物理系,长沙 410073)
2) (国防科技大学理学院数学系,长沙 410073)
超短超强激光脉冲与固体靶相互作用可通过钻孔辐射压加速机制产生百MeV 量级的离子束,离子束的品质强烈依赖于激光和靶的作用参量.本文以近400 组激光驱动固体靶的粒子模拟结果作为数据集,以激光强度、靶密度、靶厚和离子质量作为输入参量,基于全连接神经网络建立了一个离子峰值能量和截止能量连续映射模型.该模型用较为稀疏的参量取值获得了较大参量范围内的分析结果,大大减少了多维参量大范围扫参的计算量.基于连续映射模型的结果,得到了钻孔辐射压加速机制下离子峰值能量的修正公式和截止能量的拟合公式,可为激光离子加速的实验设计提供重要参考.
1 引言
随着超短超强激光脉冲与等离子体相互作用研究的不断深入,基于超强激光驱动的离子加速逐渐成为激光等离子体领域的重要研究方向,在离子束驱动快点火[1,2]、束靶中子源[3,4]、温稠密物质加热[5-7]、质子照相[8,9]等领域得到了广泛研究与应用.常见的激光驱动的离子加速机制包含辐射压加速(radiation pressure acceleration,RPA)[10,11]、靶背法向鞘层加速(target normal sheath acceleration,TNSA)[12,13]、靶破烧蚀加速[14,15]、无碰撞激波加速[16,17]等.其中,RPA 机制由于其能量转化效率高、离子束单能性好以及可加速重离子等特点,在实验上备受关注.根据固体靶厚度的不同,RPA机制可分为薄靶条件下的光帆加速(light-sail RPA,LS-RPA)[18,19]和厚靶条件下的钻孔加速(hole-boring RPA,HB-RPA)[20,21].在LS-RPA 机制下,离子与电子将被压缩为“等离子体飞镜(plasma mirror)”结构被激光脉冲整体推动加速,但这种机制对激光脉冲对比度要求较高,且靶厚度和激光脉冲强度之间有严格的匹配关系[18,19,22].而对于HB-RPA 机制,激光和靶的参数要求相对宽松,更容易在实验中实现[23],且可在较高激光强度下对重离子实现有效加速[24].
在基于HB-RPA 机制的数值模拟和实验设计中,分析研究对象与参量的关联时需进行参数扫描.然而,激光和靶参数的选取范围较为宽泛,通过开展大量实验或数值模拟进行线性扫参的代价过于高昂.同时,不同扫描参量与目标参量间可能存在一定映射关联,而通过线性扫参只能得到有限的孤立数据点,基于有限的数据建立较为可靠的连续映射关系存在较大困难.因此,有必要寻找新的研究参量映射规律的手段.近几年内,依赖于数据学习的神经网络算法[25,26]被逐渐应用在科研领域,例如托卡马克装置中磁场的控制优化[27]、惯性约束聚变实验结果对实验参数的敏感度研究[28]、电子加速能谱的自动识别与分类[29]、高辐射环境下测得的电子能谱图的去噪分析[30]、预测粒子加速器内粒子束纵向相空间演化趋势[31]等.在众多类型的神经网络算法中,卷积神经网络(convolutional neural network,CNN)主要面向二维矩阵数据的处理,在图像处理和识别等领域应用广泛[30].自组织映射神经网络(self-organizing map,SOM)的训练过程为无监督的竞争学习,适用于高维数据的聚类分析[29].全连接构型人工神经网络(fully connected neural network,FCNN)可以建立起数个变量关于单一映射量的连续模型,适用于数据回归类问题的建模分析.Djordjević等[32]基于FCNN 神经网络算法对TNSA 加速机制的多维参数进行了建模分析,得到离子截止能量的连续映射模型,并给出TNSA 机制下离子能量增大速率的连续映射模型[33].
本文所研究的HB-RPA 机制下的参数映射也是一个数据回归类问题,采用FCNN 神经网络较为适合.首先将有限的数值模拟结果整理为数据集输入FCNN,然后在数据迭代的过程中,通过神经元权重的反向传递,把目标参量关于输入参量的变化特征记录在神经网络中,从而得到连续映射模型.这一所得模型可较好反映出扫参空间中所有数据点的映射结果,并可在训练范围外进行推广,进而对更大范围的结果进行预测.本文利用FCNN建立了HB-RPA 机制下离子峰值能量和截止能量关于激光强度、靶密度、靶厚度和离子质量这4 个输入参量的连续映射模型.根据该模型与HB-RPA的理论公式及PIC 数值模拟结果的对比结果,对离子峰值能量公式进行修正,同时给出离子截止能量的经验公式,实现了对HB-RPA 机制下离子峰值能量和截止能量的定量描述.
2 物理模型
当激光强度与靶厚度近似满足a<πdn/(ncλ0)关系时,HB-RPA 机制将占主导地位[34],其中,a为归一化激光强度,与激光强度I0的关系满足a=为激光波长,d为靶厚度为等离子体临界密度,me为电子质量,ω为激光频率,e为电子电荷量.一维(one-dimension,1D)情况下,一束强度恒定为I0的圆极化激光正入射到均匀密度为n的等离子体,光束在等离子体表面被完全反射.由稳态加速离子所满足的动量平衡方程,可以得到实验室系中相对论条件下动量平衡的稳态离子能量表达式[20]:
本文通过PIC 程序EPOCH[35]对HB-RPA 过程进行了约400 次1D 数值模拟.在模拟中改变激光脉冲的归一化激光强度a,等离子体靶厚度d,等离子体靶密度n和离子质量mi,模拟参数选取范围均满足HB-RPA 离子加速机制要求.由于靶厚度d是决定HB-RPA 加速机制是否起效的重要参量,将d作为输入参量加入到神经网络的训练中,可以更好地保证训练所得模型的可靠性.在1D 数值模拟中,激光时间脉冲设置为梯形包络,如下式所示:
其中T0为激光周期,I0为激光峰值强度.等离子体为单一离子组分的平面靶,靶离子为完全电离.模拟盒子范围为 0 ≤x≤90λ0,靶前表面位置处于10λ0处.激光脉冲由左边界入射.模拟空间分辨率为 ∆x=0.01λ0,每个网格内各组分的宏粒子数目为50 个.
图1(a)和图1(c) 分别为He2+离子和C6+离子的x-v相空间图,其中,v为离子速度.x-v相空间图展现了HB-RPA 机制的典型振荡特征[20,21].在HB-RPA 机制中,激光推动电子形成压缩层,由此产生的电荷分离场把大量靶内离子加速到稳态速度,如红色虚线框所示.加速电场的峰值位于电子压缩层的前表面,随时间振荡[20],离子在振荡电场作用下形成形似鱼骨的x-v相空间结构.少量滞后的离子被加速电场的上升沿推动至峰值电场区域,进而被加速至更高能量,如蓝色虚线框所示.图1(b)和图1(d)分别为He2+离子和C6+离子在t=70T0时刻的能谱图,此时离子相空间、离子峰值能量和最大离子能量都已趋于稳定.在能谱图上略去了能量位于能谱中最低0.5%部分的低能离子,呈现清晰的准单能结构.对于每组数值模拟,通过诊断离子的x-v相空间分布来确定该组模拟中HB-RPA 加速机制占主导地位,通过离子能谱图统计离子束的峰值能量和截止能量.舍弃掉不符合HB-RPA 加速机制的数据点,最终得到400 组数据集样本数据点.
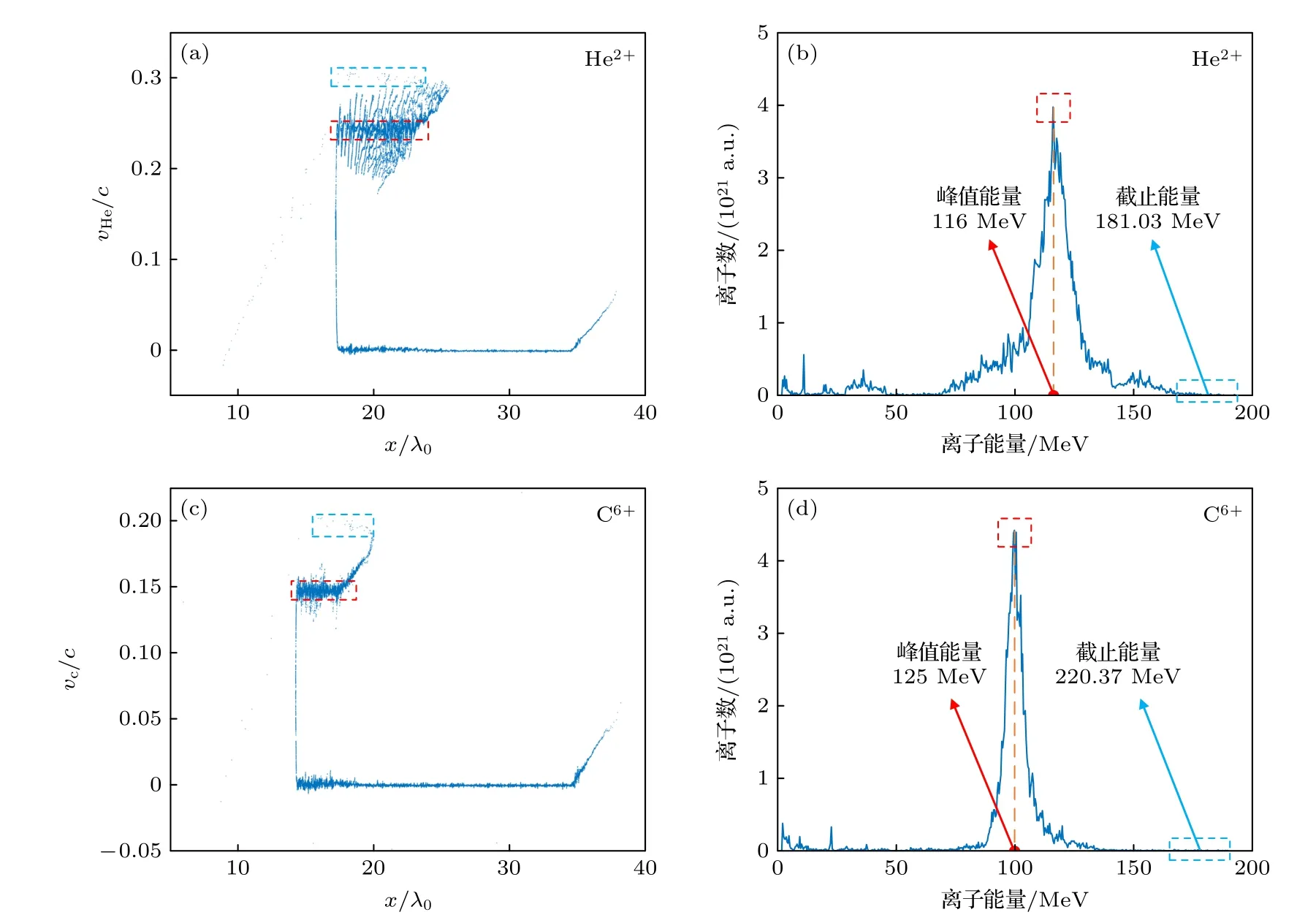
图1 在 t=70T0 时刻,(a) He2+离子的 x-v 相空间分布,(b) He2+离子的能谱分布,(c) C6+离子的 x-v 相空间分布,(d) C6+离子的能谱分布.其中,激光强度 a=100 ,靶密度 n=25nc ,靶厚 d=25λ0 ;红色虚线框内为峰值能量所对应的离子,蓝色虚线框内为截止能量所对应的离子Fig.1.At t=70T0 ,(a) the x-v phase space diagram of He2+,(b) the energy spectrum of He2+,(c) the x-v phase space diagram of C6+,(d) the energy spectrum of C6+,with d=25λ0 ,n=25nc and a=100 .The red dashed box circles the ions with peak energy,and the blue dashed box circles the ions with cutoff energy.
3 数据准备和搭建神经网络
3.1 数据集生成
整体数据集的采样采用系统抽样方式,在一定的参数范围内均匀间隔取值,通过离子种类将数据集划分为质子集、He2+集、C6+集、O8+集和测试集共5 个集合.其中,质子集合经过数据筛选后总共记录了231 次数值模拟结果,具体的输入参数取值为: 靶厚d在 [7.5λ0,35λ0] 范围内间隔 2.5λ0均匀取值,靶密度n在 [12.5nc,40nc] 范围内间隔 2.5nc均匀取值,激光强度分别取值4×1021,6×1021,8×1021,1×1022,2×1022,3×1022W/cm2.He2+离子集合包含49 次数值模拟的结果,C6+离子与O8+离子分别包含50 次数值模拟的结果,3 种离子的靶厚d取值为 15λ0和 25λ0,靶密度n在 [10nc,30nc] 范围内间隔 5nc均匀取值,激光强度取值为6×1021,8×1021,1×1022,2×1022,3×1022W/cm2.最后一个集合为独立于其他数据的测试集,离子种类包括D+,T+,He2+,B4+,C6+,F9+,Mg12+和Al13+离子,在每组数值模拟中,模拟参数d,n和a均独立取值,共20 个数据点.记录每组模拟结果的离子峰值能量Ep与截止能量Em作为训练参量,具体取值分布如表1 所列.图2(a)–(d)更直观地给出了4 种离子的参数取值分布,并用散点颜色标注了该数据点所对应的离子峰值能量.为控制输入参量的数量级相近,靶厚参数d以λ0归一化,靶密度参数n以临界密度nc归一化,激光强度以归一化激光强度a输入,离子质量以原子质量数A输入.

表1 数值模拟数据集参数取值分布Table 1. Simulation datasets prepared for neural network training.
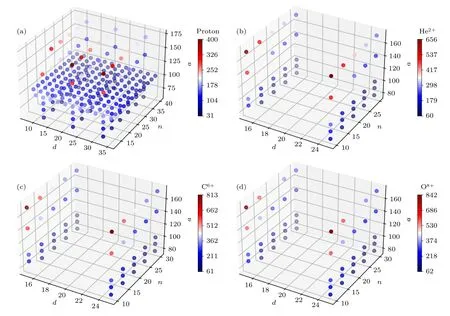
图2 离子峰值能量随输入参数 d ,n 和 a 分布的三维散点图 (a) 质子;(b) He2+ 离子;(c) C6+ 离子;(d) O8+离子Fig.2.Scatter plot depiction of ion peak energy data ensembles as a function of input parameters d,n and a: (a) Proton case;(b) He2+,(c) C6+;(d) O8+.
3.2 神经网络搭建
本文基于Pytorch 中的nn 模块来搭建深度神经网络,所采用的网络类型为FCNN,通过测试与对比训练结果对神经网络结构与超参数的选取进行调整,最终确定神经网络结构如图3 所示.经过筛选和后处理的样本数据被输入到输入层,4 个神经元分别对应输入参数d,n,a,A.经过6 个隐藏层后,结果收敛至输出层的单一输出量.Ep与Em采用相同的神经网络结构.

图3 训练所使用的神经网络结构Fig.3.Neural network architecture used in the following training.
神经网络训练参数的选取与所得到代理模型(surrogates ensemble,SE)[36]的泛化能力密切相关.我们所使用的神经网络采用均方方差损失(mean square error,MSE)函数,采用nn 模块默认的L2正则化,其中L2=2×10-5.神经元激活函数选取为Sigmoid 与PReLU,这两种激活函数皆为单调函数,模型映射曲线在有限的预测范围内保持缓慢平滑变化,这一特征与HB-RPA 理论公式相契合.训练结果表明,我们所确定的神经网络结构可使模型收敛至接近理论预测结果,同时保持了较好的平滑程度和泛化性,这使得分析参量的训练和预测结果都具有一定的可靠性.
3.3 训练与测试
针对模拟数据所展开的训练类型均为监督学习,在给定输入数据上训练神经网络,训练过程中优化器选择基于随机梯度下降的Adam 优化器,损失函数选择MSE.本文将数据集划分为380 组数据的训练集和20 组数据的测试集,训练集与测试集皆为固定.训练数据在神经网络上迭代次数固定为8000 次,学习率固定为1×10-4,损失函数误差下降至1×10-4时,模型趋于收敛,且平滑程度与拟合程度良好.
4 研究结果
4.1 神经网络集合
在初始化权值的训练条件下,每次的训练结果会略有不同.由于本文所使用的参数空间相对稀疏,每次训练所得模型的差异将会更加明显.为此,本文对10 个神经网络同时进行训练,得到一个神经网络集合,并根据模型收敛时的损失函数取值对训练结果做加权平均,从而生成训练结果的代理模型.取每个模型最后2000 次迭代的损失函数均值的倒数作为该模型的权值,对所有神经网络模型加权平均,由模型权值进行归一化,即可得到
式中,代理模型SE 是所有训练模型Si的均值;wi为每个训练模型的权值,为最后2000 次迭代损失函数均值的倒数;x为输入参数的取值;N=10 表示神经网络模型训练个数.为了衡量代理模型在一定取值范围内的可变性,定义了标准差σ:
4.2 代理模型映射
利用神经网络训练结果和加权所得的代理模型,在一定范围内的参数空间上对输入参数进行连续扫参,可得到目标参量关于不同输入参数的映射关系,并与测试集数据点进行比照.
图4 为根据神经网络代理模型所绘出的离子峰值能量与截止能量关于靶密度n和激光强度a的二维连续映射图.从图4(a) 可看出,当激光强度一定时,峰值能量Ep随靶密度的增大而减小;当靶密度固定时,峰值能量Ep随激光强度的增大而增大.当激光强度与靶密度满足保持不变时,离子峰值能量接近为定值,峰值能量Ep映射结果与(1)式理论结果符合很好.同时,图4(b)给出的截止能量Em随靶密度增大而减小,随激光强度增大而增大,与峰值能量Ep呈现出一致的映射规律.
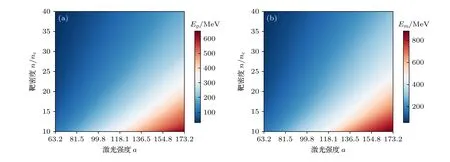
图4 He2+离子 (a) 峰值能量 Ep 与 (b) 截止能量 Em 的二维连续映射图,其中靶厚 d=15λ0 ,参数映射范围为63.2 ≤a ≤173.2和10nc ≤n ≤40ncFig.4.Two-dimensional continuous mapping of peak energy Ep (a) and cutoff energy Em (b) for He2+ over 63.2 ≤a ≤173.2 and 10nc ≤n ≤40nc with d=15λ0 .
图5 为离子峰值能量代理模型关于单个输入参量的映射曲线和峰值能量理论曲线(由(1)式给出)的比照结果.图5(a) 给出了He2+离子峰值能量随靶密度n变化的连续映射曲线,训练参数取值范围为 10nc≤n≤30nc,预测参数取值范围为30nc≤n≤50nc.由图5(a) 所示,训练参数取值范围内,代理模型与理论曲线和测试集数据吻合程度相当好;在预测参数取值范围内,模型映射值与测试集数据偏差小于10%,模型的可靠性可以得到保证.而当n>50nc时,模型映射值与理论值相差超过10%,模型的可靠性不好,所以这里没有给出映射结果.若增大训练参数取值范围,则可在更大范围内保证模型预测的可靠性.
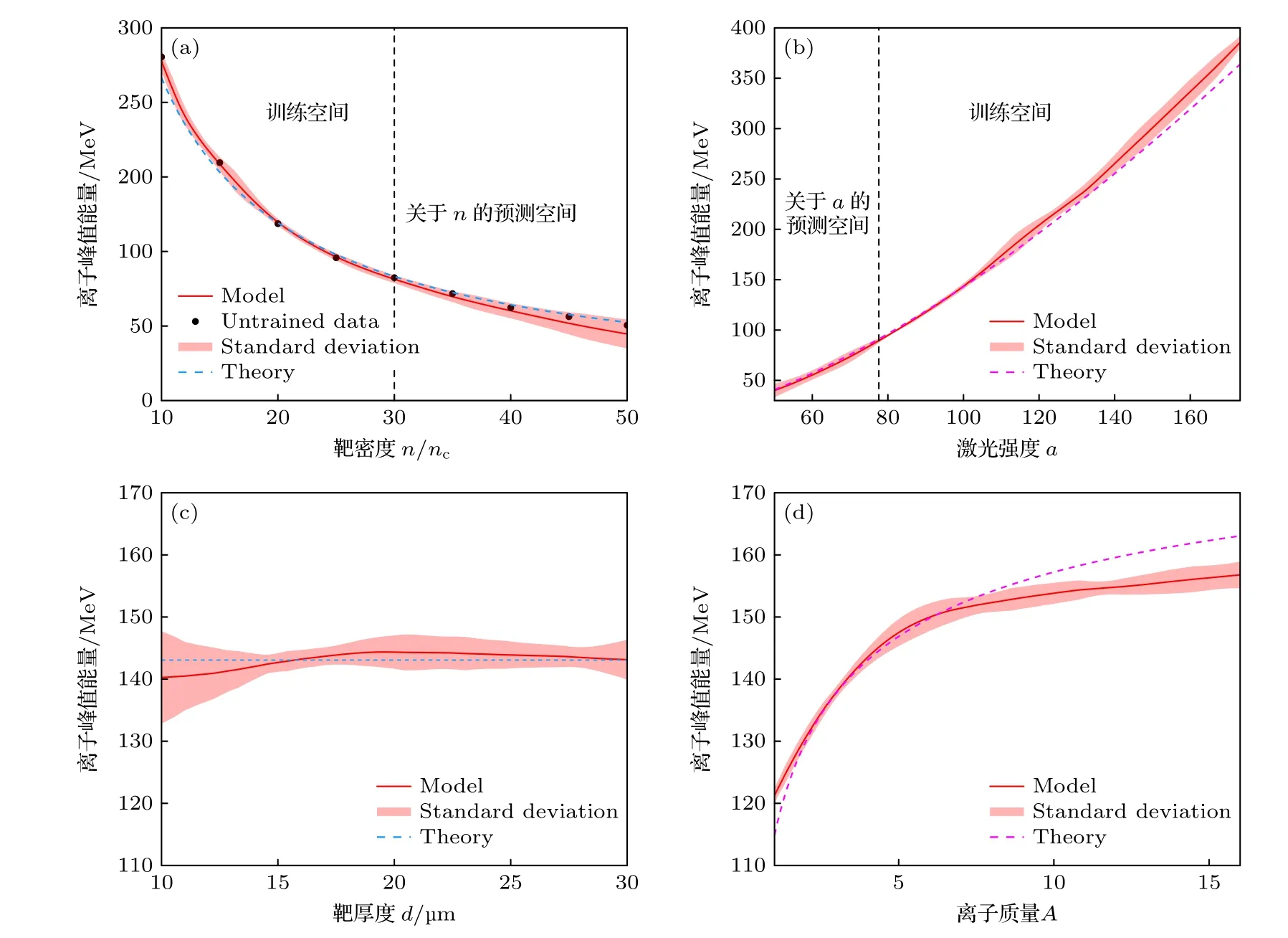
图5 (a) He2+离子 峰值 能量 Ep 关于靶密度 n 的映 射曲线,其中靶厚 d=15λ0 ,激光强度 a=100 ;(b) He2+离 子峰 值能量Ep关于激光强度 a 的映射曲线,其中靶厚 d=15λ0 ,靶 密度 n=20nc ;(c) He2+离子峰值 能量 Ep 关于 靶厚 d 的映射曲 线,其中 靶密度 n=20nc ,激光强度 a=100 ;(d)离子峰值 能量 Ep 关于离子质量数 A 的映 射曲 线,其中靶厚 d=15λ0 ,靶密度 n=20nc,激光强度 a=100 .图中红色实线为代理模型的映射曲线,模型标准差用红色色块填充于代理模型曲线两侧.蓝色虚线给出的是根据HB-RPA 机制理论公式所绘出的离子峰值能量随离子密度变化的曲线,黑色实心数据点为测试集数据点,参数取值范围与模型预测范围用黑色虚线分隔Fig.5.(a) Parameter scan of He2+ peak energy Ep over target density n with d=15λ0 ,a=100 ;(b) parameter scan of He2+peak energy Ep over laser intensity a with d=15λ0 ,n=20nc ;(c) parameter scan of He2+ peak energy Ep over target thickness d with a=100 ,n=20nc ;(d) parameter scan of ion peak energy Ep over ion mass number A with a=100 ,n=20nc and d=15λ0 .The SE mapping curves are drawn with red solid,the theoretical curves are drawn with dashed,the red filled region indicates the standard deviation,and the untrained data from test subset are drawn with black dot.
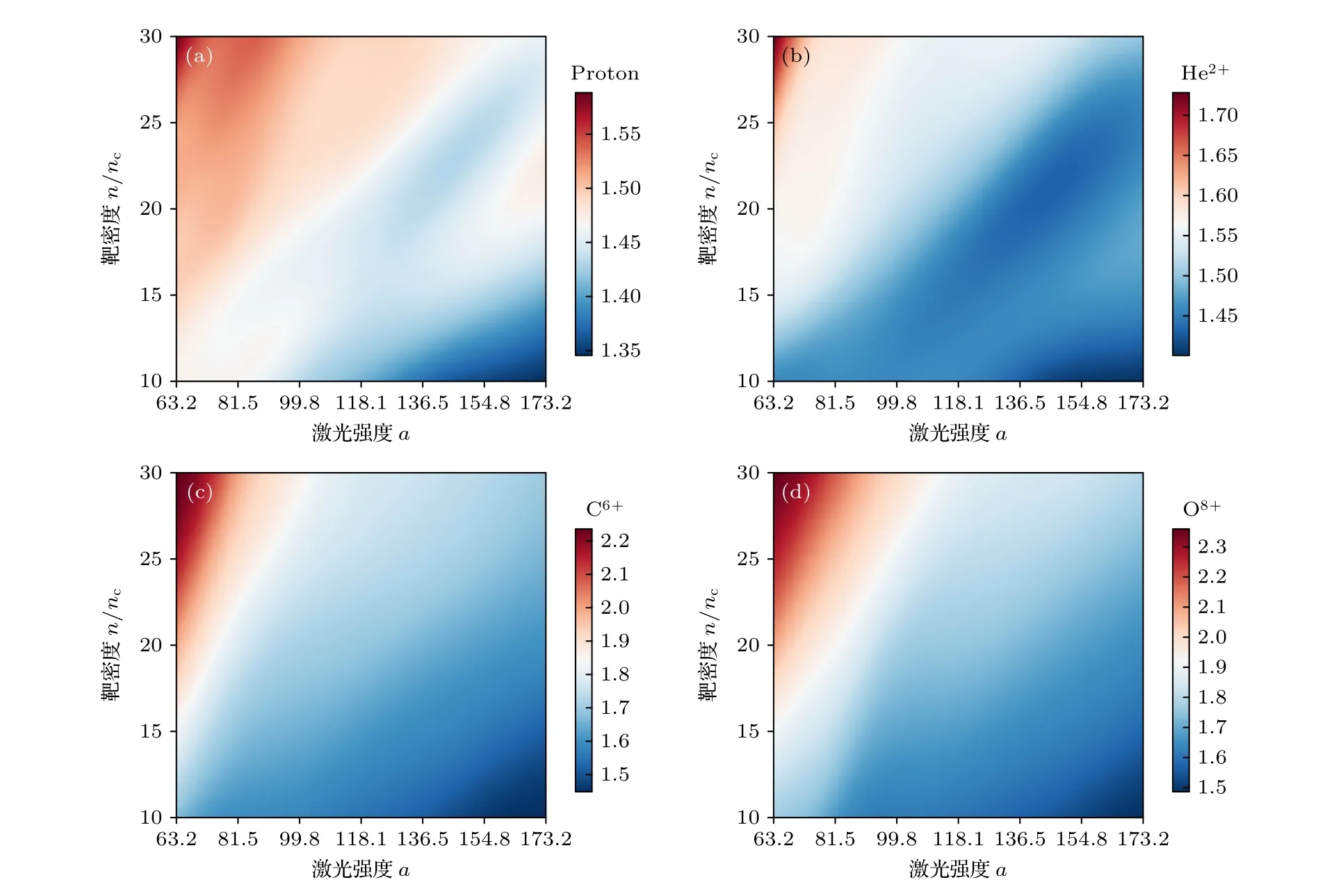
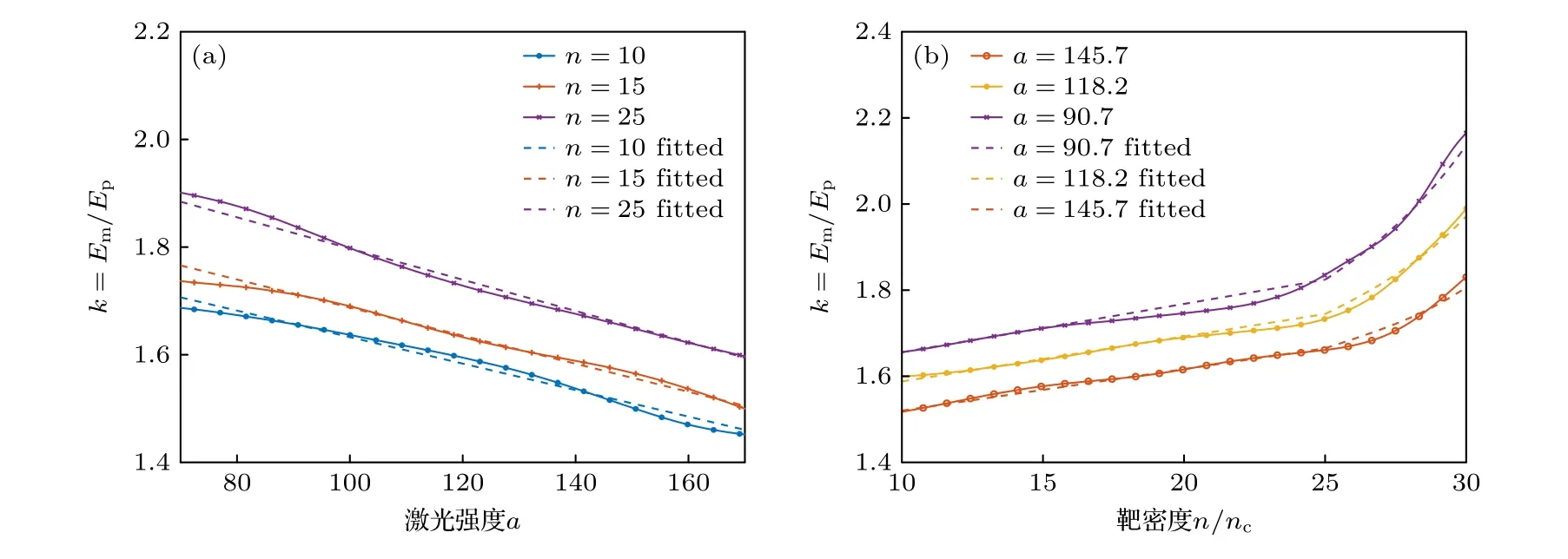
图5(b)给出了He2+离子峰值能量与激光强度a的模型连续映射曲线.激光强度的训练参数取值范围为 77.5 4.3.1 峰值能量修正 图5(d) 展现出映射曲线与理论曲线存在偏差,离子峰值能量在质量较低时略高于理论值,而在质量较高时略低于理论值,模型曲线与理论曲线于离子质量数A=5 附近相交.对比了更大范围的数值模拟结果与理论值,发现这一偏差仍然存在.结合代理模型所给出的模型和测试集所得模拟数据,对原理论公式进行修正,修正后的公式可描述离子质量对离子峰值能量的影响: 式中,A为离子质量数.经过修正的模型曲线与测试集数据点对比如图6 所示. 图6 在 d=15λ0 ,n=20nc 和 a=100 下,离子峰值 能量随离子质量的变化Fig.6.Ion peak energy scan with ion mass number A with d=15λ0,n=20nc and a=100 . 如图6 所示,当质量数A>5 时,数值模拟结果与理论曲线开始出现偏移.当质量数A>10 时,模拟结果与理论结果差异逐渐增大,误差率接近10%左右.当采用基于离子质量数的修正公式时,理论结果与数值模拟结果及模型映射结果符合很好.对于质量数A>30 的中高Z离子,其较为复杂的电离过程将对离子的加速过程产生影响.在电离度较低的情况下,重离子将滞后于电子被推动形成的钻孔活塞结构,此时HB-RPA 模型不再适用,离子峰值能量将显著低于理论值[21].因此,这里基于映射结果给出的修正模型仅适用于A<30 的靶材料.在质量数A>30 时,需增大数据集的质量数取值范围,并考虑靶材料的离化过程对加速过程的影响. 4.3.2 截止能量映射 当离子截止能量作为目标参量时,重复与离子峰值能量相同的训练和扫参操作,可以得到连续映射曲线,如图7 所示. 图7 (a) He2+离子截止能量 Em 关于靶密度 n 的映射曲线,其中靶厚 d=15λ0 ,激光强度 a=100 ;(b) He2+离子截止能量Em关于激光强度 a 的映射曲线,其中靶厚 d=15λ0 ,靶密度 n=20nc ;(c) He2+离子截止能量 Em 关于靶厚 d 的映射曲线,其中靶密度 n=20nc ,激 光强度 a=100 ;(d) 离子截止能量 Em 关于离子质量数 A 的映射曲线,其中靶厚 d=15λ0 ,靶密度 n=20nc,激光强度a=100Fig.7.(a) Parameter scan of He2+ cutoff energy Em over target density n with d=15λ0 ,a=100 ;(b) parameter scan of He2+cutoff energy Em over laser intensity a with d=15λ0 ,n=20nc ;(c) parameter scan of He2+ cutoff energy Em over target thickness d with a=100 ,n=20nc ;(d) parameter scan of ion cutoff energy Em over ion mass number A with a=100,n=20nc and d=15λ0 . 图7 给出了He2+离子的截止能量关于靶密度n、激光强度、靶厚和离子质量的映射关系.结果表明,离子截止能量随n的增大而减小,随激光强度的增强和离子质量的增大而上升,而与靶厚无明显关联.离子截止能量的映射结果与离子峰值能量的映射结果呈现出一致的单调性变化规律.因此,将结合 离子峰值能量Ep与离子截止能量Em的比值映射模型给出HB-RPA 机制下离子截止能量的经验公式. 4.3.3 能量比值关系 将每组模拟截止能量Em和峰值能量Ep的比值记为k=Em/Ep.将k作为建模参量,神经网络结构与超参数设置均与训练Ep和Em时保持一致,损失函数阈值设为2×10-4,重复与Ep,Em类似的训练和代理模型加权平均操作,得到k关于不同输入参量的映射模型. 图8 为质子、He2+、C6+、O8+四种离子的截止能量Em与峰值能量Ep的比值k的二维连续映射图.由图8(a) 所示,质子的能量比值k随靶密度n增大而增大,随激光强度a增大而减小,k值在较小范围内缓慢变化且近似均匀.在a<90 ,n>25nc的部分区域,k变化幅度增大,呈现出一定非线性变化趋势.图8(b)–(d)显示,其他3 种离子的k值变化趋势与质子相同,且k值的变化范围随离子质量数A的增大而增大. 图8 (a) 质子,(b) He2+,(c) C6+和 (d) O8+的能量比值 k=Em/Ep 的二维连续映射图,其中靶厚 d=20λ0,参 数映射范围 为63.2 ≤a ≤173.2 和10nc ≤n ≤30ncFig.8.Two-dimensional continuous mapping of k=Em/Ep over 63.2 ≤a ≤173.2 and 10nc ≤n ≤30nc with d=20λ0 :(a) Proton case;(b) He2+;(c) C6+;(d) O8+. 图9 为能量比值k随激光强度和靶密度变化的映射曲线.图9(a)显示,k随着激光强度a的增大近似以线性规律减小,其斜率随靶密度增大而增大.图9(b)显示,当n<25nc时,k随着靶密度n的增大而近似线性增大;当靶密度n>25nc时,k的上升幅度显著变大,呈现非线性变化趋势.前面图1 中关于离子相空间的分析已给出: 峰值能量对应的离子主要在电荷分离场的峰值区域内被加速;而截止能量对应的离子先被电荷分离场的上升沿预加速,再进入峰值区域被加速,所以具有更高的能量.当激光强度较大或靶密度较低时,电荷分离场峰值强度增加,导致离子峰值能量增大,截止能量与峰值能量差距减小.当激光强度较小或靶密度较高时,电荷分离场峰值强度降低,离子受电荷分离场上升沿加速所获得的能量占比增大,导致截止能量与峰值能量差距增大.综合上述映射模型特征和物理过程分析,给出了能量比值k关于输入参量的拟合公式: 图9 C6+离子能量比值 k 随(a)激光强度和(b)靶密度的映射曲线(实线)和拟合公式结果(虚线),其中参数范围分别为63.2 ≤a ≤173.2,10nc ≤n ≤30nc ,靶厚d=15λ0Fig.9.Parameter scan (solid) and fitted formula (dashed) of k over (a) 63.2 ≤a ≤173.2 and (b) 10nc ≤n ≤30nc for C6+ with d=15λ0. 在n<25nc时,(5)式中第1 项描述了k关于激光强度a的线性变化趋势,以及靶密度n和离子质量数A对激光强度映射的影响;第2 项和第3 项反映了靶密度n和离子质量数A对k值整体取值分布的影响.n>25nc时,第1 项与第2 项中靶密度n增加了高次项,描述了在较大密度下能量比值关于n变化的非线性趋势,此时上升幅度增大.离子截止能量Em可以由下式给出: 本文基于FCNN 算法对粒子模拟所生成的数据集展开了分析,建立了HB-RPA 机制下离子峰值能量和截止能量关于激光强度、靶密度、靶厚度和离子质量的连续映射模型.该模型在与测试集数据和理论公式的比对中表现良好,且具有一定参数范围内的预测能力.研究发现,当离子质量数较大时,HB-RPA 机制下的峰值能量公式与数值模拟结果存在差异.基于映射模型和数值模拟结果,给出了离子峰值能量的修正公式和离子截止能量的经验公式.在基于HB-RPA 的激光加速离子实验设计中,我们的映射模型和经验公式可为激光和靶参数的选取提供重要参考.本工作也可以拓展到更多样化的目标参量,对离子束产额、单能性和准直度等束流品质进行分析.4.3 离子的峰值能量和截止能量


5 结论与展望
