基于有限元方法的半钢两次法第一段成型机主轴支承跨距分析

张波

（北京敬业机械设备有限公司，北京 100194）

1 问题的提出

近年来随着轮胎规格的不断变化和发展，用户对我公司轮胎成型机的要求呈现出以下变化趋势：规格参数范围增大、主轴悬伸加长，轴端负载增大并且要求缩减设备尺寸。为了适应市场及用户的需求，现针对我公司已有的LCY1520 型第一段成型机主轴部件进行分析，计算主轴支承跨距的变化对主轴部件的静刚度影响，以便对公司设备的设计及改进提供理论参考。

主轴的静刚度简称为主轴刚度，其反映了主轴部件抵抗静态外载荷的能力，与主轴的负荷能力、抗震性能等密切相关[1]。主轴刚度是影响轮胎成型机在轮胎贴合及成型时精度的主要因素之一，是成型机设计时的重要考量指标。主轴刚度的影响因素较多，主要有：主轴的直径、主轴的悬伸量以及合理的支承跨距等。对于本案分析而言，由于成型机规格已经确定，因此主轴部件的直径和悬伸量均为不易变动的值，所以主轴部件的最佳支承跨距计算，就成为设备设计、优化和改进的主要环节。目前通常的分析方法是将主轴部件简化为两支承的悬伸简支梁，根据材料力学中的变形位移线性叠加原理，从而得到计算公式[2]。

对于成型机主轴部件而言，大多是阶梯轴并且主轴内部分布有不同的长孔，因此用材料力学公式精确计算主轴部件的最佳支承跨距是非常困难的。而今天有限元计算方法的成熟，特别是有限元计算软件的普及对于计算主轴部件的最佳支承跨距提供了有效而便利的手段。

2 问题的分析

2.1 主轴部件模型的简化

要计算主轴部件的最佳支承跨距，需要先将主轴部件简化为合理的力学模型，为后续建立有限元计算模型做好准备。

图1 是LCY1520 型第一段成型机的主轴部件示意图，主要由阶梯主轴、作为前支承的两个单列圆锥滚子轴承、作为后支承的一个深沟球轴承以及作为传动扭矩输入的同步带轮组成，外部载荷作用于主轴的前端。对本案分析而言，主要考察主轴部件受外部载荷后的弯曲变形量，为了减少计算量，此处忽略同步带轮传动扭矩的影响。依据材料力学的相关原理及公式，将本系统简化为图2 所示的力学计算模型[3]。

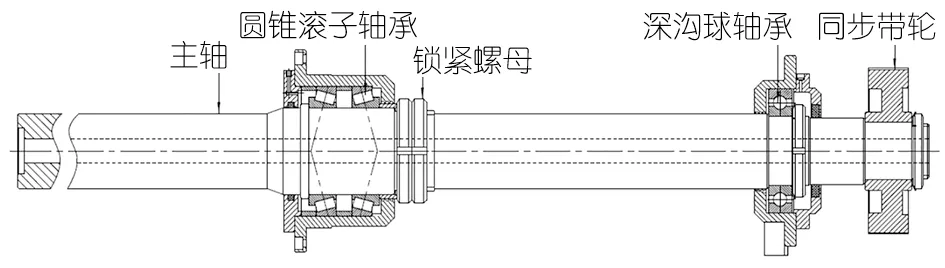
图1 主轴部件示意图

图2 计算模型简化图

对于本案分析而言，以图2 中的参数均为已知数值，下面将各已知参数列在下方，供之后计算时使用：

轴端受力：

m— 轴端负载质量，m=150 kg ；

g— 重力加速度，g=9.8 m/s2。

当前主轴悬伸量：a=1 466 mm ；

当前主轴支承跨距：L=756 mm。

2.2 主轴挠度的计算方式

对于主轴部件端部的总挠度，是由主轴本身的弯曲变形和主轴支承处的弹性变形叠加引起的，一般用下式表示[4]：

式中：

y— 主轴端部总挠度；

y1— 主轴弯曲变形引起的主轴端部挠度；

y2— 主轴支承处弹性变形引起的主轴端部挠度。

首先假设主轴的支承为刚性体，主轴本身为弹性体，主轴端部受力F后的挠度为y1，计算公式如下所示：

式中：

F— 主轴端部受力；

E— 主轴材料的弹性模量；

I— 主轴截面的平均惯性矩。

再假设主轴的支承为弹性体，主轴为刚性体，主轴端部受力F后的挠度为y2，计算公式如下所示：

将式（4）（5）代入式（3），可得：

式中：

δA— 支承A处的弹性变形量；

δB— 支承B处的弹性变形量；

KA— 支承A处的径向刚度值；

KB— 支承B处的径向刚度值；

FA— 支承A处的支反力；

FB— 支承B处的支反力。

3 模型的计算

3.1 y1 值的计算

有限元方法的基本思想是把连续的构件离散成有限数量的单元，并且在每个单元中设定有限个数的节点，将连续的构件看成是只在节点处相连接的一组单元的集合体；同时选定场函数的节点值作为基本未知量，并在每个单元中假设一个近似插值函数来表示此单元中场函数的分布规律；进而利用力学中的某些变分原理去建立用以求解节点未知量的有限元方程，将一个连续域中的无限自由度问题转化为离散域中的有限自由度问题[5]。

具体到本案分析中，计算y1值时，首先建立主轴部件的三维模型，然后将三维模型导入ANSYS 软件中。在给三维模型赋予材料属性时，由于本案分析主要考察主轴支承跨距的变化对主轴端部总挠度的影响，并且碳钢与合金钢的弹性模量差别不大[3]，因此将三维模型赋予“ 结构钢” 材料即可。在网格划分时采用四面体实体单元，可以兼顾分析的精确性和计算速度，是比较合理的单元类型选择。在添加边界条件时，两处支承处的约束施加是分析能否成功的关键所在。由于在ANSYS 软件中，实体单元只有平移自由度而没有旋转自由度，与铰支点的自由度要求不符。因此此处的约束应采用“Remote Displacement”，将此处约束简化为一个质量点，然后就可以释放此处的旋转自由度，通过设置参数，达到与铰支点自由度相符的条件，具体设置见下图3。

图3 主轴支承处约束设置

图4 主轴径向变形云图

图5 主轴支承处支反力

由于支承A处既起到支撑主轴的作用又起到约束主轴轴向位移的作用，因此约束A处的X、Y、Z三个方向的平移自由度和X、Z轴的旋转自由度，释放Y轴的旋转自由度；而支承B处只起到支撑主轴的作用，因此约束B处的Y、Z两个方向的平移自由度和X、Z轴的旋转自由度，释放X方向的平移自由度和Y轴的旋转自由度，至此完成两个支承处的约束设置。

施加外部载荷时，由于主轴较长，质量较大，主轴的自重影响不可忽略，因此除施加外部载荷外还需要施加重力场，其方向应与外部载荷方向一致，外部载荷为已知量，F=1 470 N。

上图是经计算后得到的在外部载荷F=1 470 N 作用下，施加了标准重力场，将主轴变形量放大560 倍后的径向变形云图，由此可得y1=1.068 8 mm。

3.2 y2 值的计算

在计算y1值完成后，可以直接探测支承处的支反力，由此计算支承处的弹性变形量。

对于支承处的径向刚度值，除了轴承本身的刚度值外，轴承座的刚度、支撑箱体的刚度以及加工装配都是重要的影响因素，想要精确的计算出支承处的刚度值非常困难。考虑到设备已经投入使用，因此支承处的刚度值已经是一个定值，此处径向刚度值仅取轴承本身的数值。支承A 处为两个圆锥滚子轴承，型号：32030 ；支承B 处为一个深沟球轴承，型号：6224 ；按照手册的图表查得[5]：

代入式（3）（4）后，计算得到y2= 0.018 5 mm。

4 主轴支承跨距变化后的挠度计算

由以上的计算可知，当前设备的主轴部件端部总挠度y= y1+y2=1.087 3 mm。为了分析主轴支承跨距变化对挠度的影响，在当前跨距L 的基础上，以50 mm长度为分隔单位，分别减小13 个单位和增加20 个单位来计算主轴部件端部总挠度y，结果见下图6。

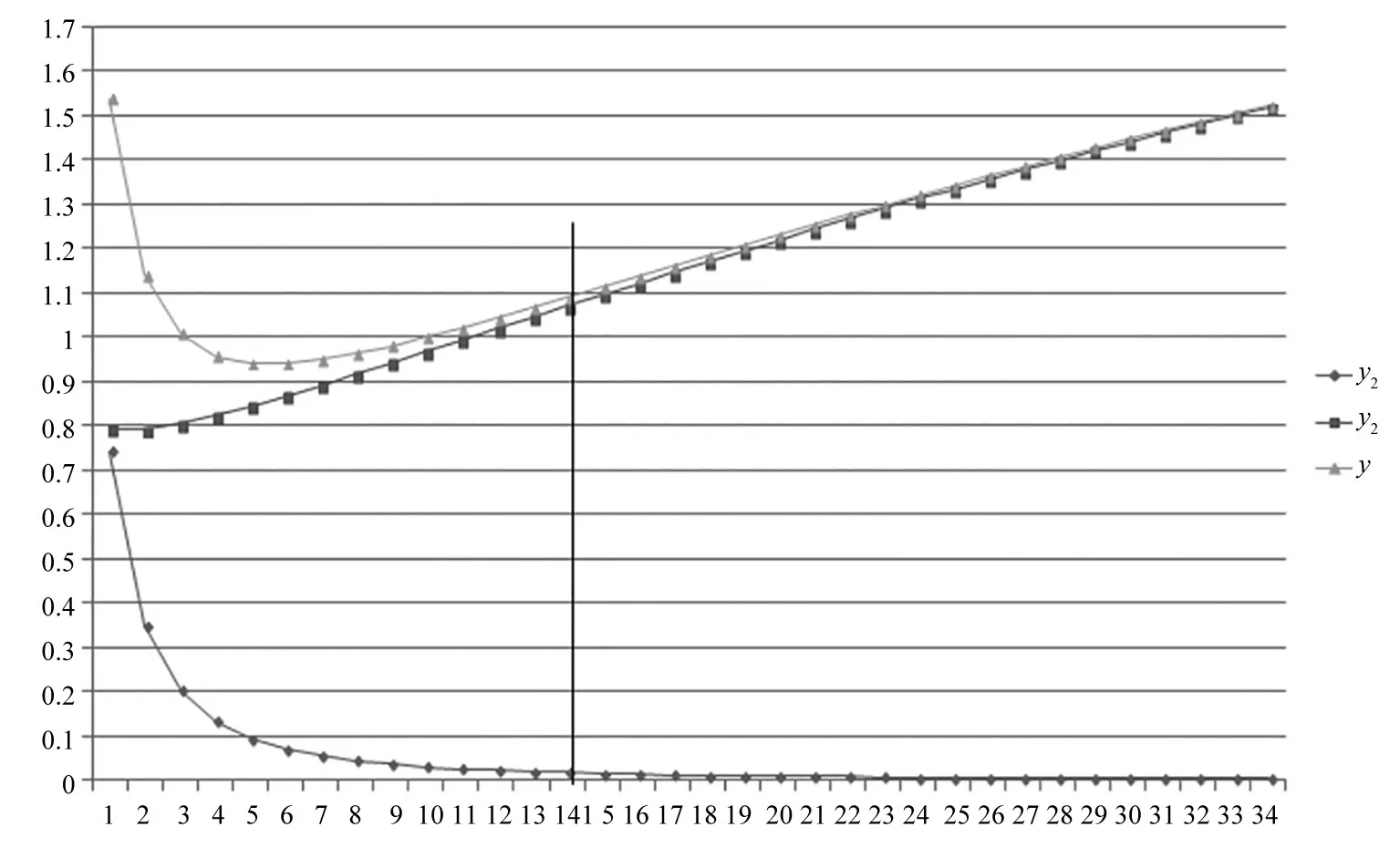
图6 主轴支承跨距变化时的轴端挠度计算值

图6 中，纵轴为轴端挠度计算值，单位为mm ；横轴为分隔单位数，共计34 个计算单位，其中序号14 为当前设备的计算值。由上图可以看出，主轴支承跨距在序号5 附近时，主轴部件端部总挠度y 值最小，刚性最好。

5 结论

通过对已有设备的主轴建立有限元模型，并按照实际使用情况进行了模拟计算，结果显示本设备可以通过适当的减小主轴支承跨距来达到增加主轴刚性，减少设备占地面积，降低零件加工难度的目的。另外，主轴的支承跨距和支承处的径向刚度值是优化设备时的重要影响因素，本文为公司其它相同类型产品的设计及优化改进提供了一种参考思路。