室内三维环境重建技术中的立体匹配算法研究与仿真
2023-10-05管阳
管阳
(陕西国防工业职业技术学院艺术与设计学院,陕西西安 710300)
据统计,人类83%的信息获取来自于视觉。近年来,随着计算机视觉的发展,三维重建技术(3D Reconstruction)取得了长足的进步[1-4]。而室内三维重建将现实的二维图像通过图像提取、特征提取及立体匹配(Stereo Matching)等流程转化为计算机可投影的立体图像,且在室内设计领域得到广泛的应用。该技术在人体双目线索感知距离原理的基础上,利用计算机获取三维信息。在实现三维重建的过程中,需借助两个及以上的摄像机对同一物体从不同位置成像,再基于相机间的视差计算距离深度信息,进而实现对物体的三维描绘。利用两台计算机对同一场景进行像素点搜寻并获取视差的过程,称为立体匹配。传统的立体匹配算法主要通过图像特征线、扫描线等计算初始视差,同时基于能量函数的迭代实现最优视差图的搜索。但这类算法对于弱纹理、部分遮挡及深度不连续等特征的提取效率偏低,匹配精度也较差,故无法满足三维重建的要求[5-11]。
基于上述分析,该文基于深度学习(Deep Learning,DL)网络对传统的立体匹配算法进行了改进,并设计了一个用于代价匹配特征提取的计算网络,进而避免了人工构造匹配代价的繁琐流程。同时还引入基于十字窗口的代价聚合方法(Cross-Based Cost Aggregation,CBCA),显著提升了立体匹配算法的效果,为三维重建打下了坚实基础。
1 理论基础
1.1 室内三维视觉重建技术
室内三维重建技术的基本原理如图1 所示[12]。
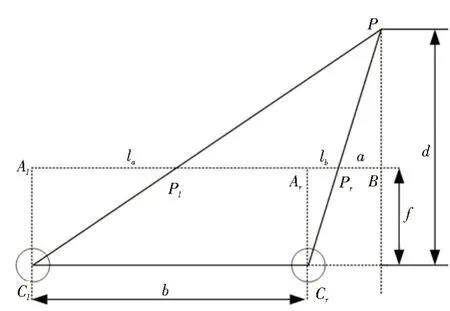
图1 三维重建基本原理
图1 中,P为待成像的物体;Cl、Cr均为摄像头,且二者的间距为b。记AlPl的距离为la,ArPr的距离为lb,PrB的距离为a,则根据相似三角形的几何原理可得:
式中,摄像头的焦距f、镜头间距b为已知量。式中以a、d为未知量,可求得:
式中,la-lb为左右相机间的视差,其描绘了图像点P在两个相机间的位置差异,而立体匹配就是在左右相机图像间寻找对应点的过程。
基于上述讨论,得到三维重建的基本过程如图2所示。

图2 三维重建基本过程
其中,立体匹配是三维重建中最关键的步骤。由于三维场景在摄像机中被投影为二维图像,故同一物体在不同视角感知下所得到的图像也不尽相同。此外,其还会受现场光照、噪声、畸变及摄像机特性等多重因素的干扰。因此,文中对立体匹配算法做了进一步的研究。
1.2 立体匹配算法
立体匹配算法的输出结果是视差图[13-14],传统算法的步骤主要包括匹配代价的计算、代价聚合、视差计算与视差优化共四步。而传统的误差匹配算法面临着物体遮挡、弱纹理区匹配误差较大、深度不连续区视差不平滑以及物体边缘模糊等问题。为了克服传统方法的不足,该文采用深度学习网络进行特征的提取与匹配代价的计算。具体的网络结构如图3所示。

图3 匹配代价提取网络
由图可知,网络对于数据集中的左、右图像分别建立了结构对称的深度学习网络。且两个网络间权值共享,并主要通过卷积运算、ReLU 函数来获得初始的匹配代价:
其中,Gw(X1)、Gw(X2)分别为卷积网络输入的特征向量,Ew()
X1,X2为相似度判别函数。卷积运算与ReLU 函数的计算方分别如下所示:
式中,A、B为参与卷积的矩阵,Mr、Mc为矩阵的行、列。由于视差图的像素点并非独立分布的,所以为了在立体匹配过程中计算像素点间的关联性,该文在代价聚合时引入了一种十字窗口聚合法,具体如图4 所示。
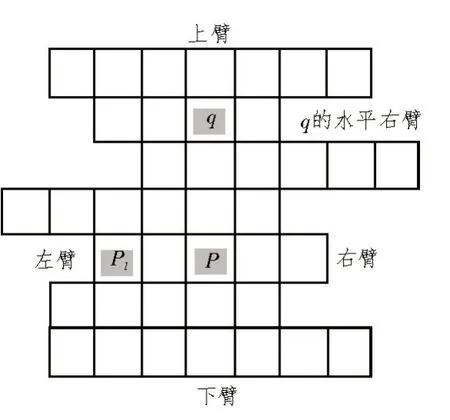
图4 十字窗口代价聚合
对于图4 中的十字窗口,任意像素点p的臂长约束条件为:
式中,I为像素强度,τ和L1分别为像素强度、像素间距的阈值。根据该约束条件,可得到范围为d的十字窗口联合支持域Ud(p)为:
式中,UL为左图支持域,UR为右图支持域。对该区域内所有像素点进行代价聚合C+的方式如下:
其中,CCNN()为深度学习网络的代价函数。
为了保证算法的训练效率,避免模型的过拟合,引入了一种基于自适应矩阵估计的适应性矩估计(Adaptive moment estimation,Adam)优化方法进行训练迭代:
式中,mt为t时刻的一阶矩阵估计,vt为二阶矩阵估计,gt为损失函数的梯度,βi是矩阵估计量的衰减因子。使用衰减因子修正后的矩阵估计为:
从而得到最终的参数优化方式如下:
式中,θ为模型参数,η为训练过程中的基础学习率,ε为矫正因子。
2 方法实现
2.1 仿真实验设计
该文评估算法性能时,使用了立体匹配算法常用的公开数据集Flyingthings3D[15-16]。该数据集的具体参数如表1 所示。

表1 Flyingthings3D具体参数
为评估立体匹配算法的性能,使用误匹配率(SPBM)、平均绝对误差(SMAE)与均方误差(SMSE)作为评价指标。这三个指标的定义分别如下:
式中,dc为算法输出的视差图,dT是实际的视差图,且视差图的像素点均为N,δ为统计过程中使用的误差阈值。该文所使用的网络结构参数如表2所示。
在对网络进行训练时,采用Adam 优化方法,同时引入了批处理策略,且批处理大小为256,训练的目标误差为10-8。此外,为了避免训练过程中出现过拟合,网络学习率采用了上文所述的动态调整策略,各阶段的基础学习率如表3 所示。
为了提升网络的训练效率,并对其进行合理的评估,实验环境如表4 所示。
2.2 算法仿真结果
图5 给出了数据集中部分图像在表2 网络下的立体匹配效果,其中左侧为同一组,而右侧为另一组。从图像匹配效果看,该算法输出的视差图与真实图基本一致,且无明显的视觉差异。

表2 网络结构参数

表3 各阶段基础学习率

表4 算法仿真软硬件环境
为了进一步测试所提算法相较于现有模型的性能差异,将其与当前主流的立体匹配算法EDP(Edge-aware Disparity Propagation)、多通道卷积神经网络(Multi-Channel CNN,MC-CNN)等算法进行了对比。以数据集中某图像的匹配为例,利用三种算法分别进行训练,效果如图6 所示。

图5 部分图像立体匹配效果

图6 不同算法下的训练结果
在图6 的对比区域中,图(a)的真实视差图包含了丰富的边缘信息;图(b)中的边缘模糊,细节缺失较多;图(c)虽然展现了边缘信息,但视差图存在孔洞,图层之间也出现了交叠;而图(d)中边缘信息保留的更为丰富,且实线框内的物体轮廓清晰,匹配效果显著优于图(b)和(c)。对三种算法的指标数据进行统计,结果如表5 所示。
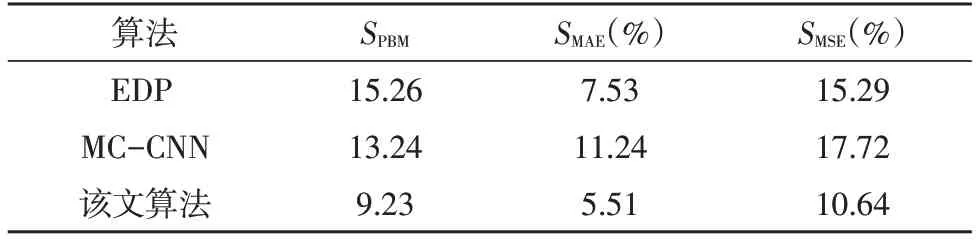
表5 模型指标数据
从表中可看出,该算法的SPBM、SMAE与SMSE等指标较对比算法均有一定程度的改善。其中,SPBM下降至9.23,相较于两种对比算法分别降低了39.52%、30.29%;而SMAE下降至5.51%,与对比算法相比分别下降了2.02%、5.73%;SMSE则下降至10.64%,相较EDP、MC-CNN 分别下降了4.65%、7.08%,立体匹配效果显著提升。
3 结束语
该文对室内三维重建技术进行了研究,通过改进传统立体匹配算法中的代价计算方式,从而降低了立体匹配算法的误匹配率等指标。此外,算法还引入了一种基于十字窗口的代价聚合方法,从而能够有效提取像素感受野内的相关性信息,提升算法对于边缘信息的描绘能力。
