整车主动悬架系统分布式滚动时域一致性估计

宋秀兰,周文乐,徐晨辉,何德峰

(浙江工业大学信息工程学院,浙江杭州 310023)

1 引言

悬架系统作为车辆的重要组成部件,近年来受到了学术界和工业界的广泛关注.主动悬架不仅设置弹簧和阻尼器支撑车身,还设置了主动调整的执行设备,能在变化的行驶环境和随机路面激励的情况下主动输出匹配的动力,从而为车辆提供更好的可操控性和乘坐舒适性[1-2].同时在许多情况如车辆转弯、加减速过程中,主动悬架有助于降低交通事故发生的风险[3].为了实现主动悬架的预期性能,研究人员提出了很多控制算法,如模型预测控制[4]、自适应控制[5]、H∞控制[6-7]等.然而这些方法大多假设悬架系统的状态可在线测量,但这在实践中很难实现或者实现成本较高,因此,有必要建立一种有效的悬架系统状态估计框架,为悬架系统高效控制和监测提供准确可靠的状态信息.

针对主动悬架系统的状态估计问题,文献[8-9]对1/4车辆悬架系统进行了状态估计,文献[10-11]提出了针对半车主动悬架系统的估计方法,但这些1/4悬架和半车悬架系统均不能描述整车的全部状态.文献[12-15]针对整车主动悬架系统进行了估计,即估计了与整车姿态相关的所有系统状态,但估计过程采用的集中式方法需要大量复杂的计算.为了降低估计的计算量,文献[16]采用了一种分布式传感系统的设计,使用扩展卡尔曼滤波来融合测量值,估计车辆的相关状态用于主动悬架的控制.文献[17]提出了一种针对整车悬架的分布式融合滤波算法,与集中式结构相比减少了估计中的复杂计算.目前这些分布式方法没有考虑估计过程中系统状态和干扰的约束.为此,文献[18]对主动悬架进行了分布式状态估计,首先传统分散式滚动时域估计(moving horizon estimation,MHE)方法在存在约束的条件下进行估计,然后通过本地子系统与邻居之间的耦合性利用邻居信息补偿估计误差,从而在考虑约束的情况下增加了分布式估计的准确性.

本文考虑整车主动悬架系统的约束状态估计问题,提出一种基于一致性原理的分布式滚动时域估计(distributel MHE,DMHE)算法.为了降低整车主动悬架系统状态估计的计算量,首先,将整车主动悬架系统分解为若干个耦合的降阶子系统,再考虑本地子系统与邻居状态的相关性,采用一致性原理利用邻居子系统信息提高估计精度,在一次采样间隔中执行多次一致性原理进行信息融合.进一步,通过Lyapunov稳定性定理建立了估计误差系统的渐近稳定性.最后,通过对整车主动悬架系统的对比仿真验证了所提算法的有效性.

2 问题描述

考虑具有7个自由度的整车主动悬架动力学模型,由簧载质量和非簧载质量两部分组成,如图1所示.假设车身是一个刚体,Ms表示模型的簧载质量,当车辆在水平路面做匀速直线运动时,车身具有升降、俯仰和侧倾3个运动的自由度.车轮及其相连接的轴承由非簧载质量Mus表示,4个独立的悬架各具有1个垂直运动的自由度,其非簧载质量均等.令每个独立悬架由刚度系数为ks的弹簧、阻尼比为cs的阻尼器以及可以施加力的执行器的组合来建模,其中:zi和qi分别表示簧载质量和非簧载质量中第i个独立悬架的位移,wi和ui分别表示第i个悬架对应的未知道路扰动和阻尼力,z表示车身质心垂直方向上的位移,kt表示轮胎的刚假设度系数,ϕ和θ分别表示车身侧倾和俯仰角度,Ix和Iy分别表示侧倾和俯仰的转动惯量.

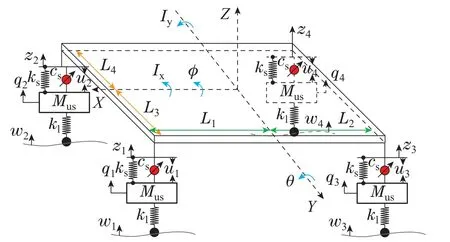
图1 整车主动悬架系统示意图Fig.1 Schematic diagram of full-car active suspension system

根据车身升降、俯仰和侧倾以及独立悬架振动等姿态,考虑悬架系统的动力学微分方程如下[18]:

其中: 主动悬架系统时间变量为t∈{0,1,···};输出变量为y=col(y1,y2,···,y7);控制输入向量为u=col(u1,u2,u3,u4);过程干扰为w=col(w1,w2,w3,w4);以及矩阵A,B和Br是与车辆悬架对应的常数矩阵,分别表示系统的状态向量x随时间的变化率与其自身、控制输入ut和相应过程干扰wt的相关性;C和D为适当维数的常数矩阵.注意,对于配置有主动悬架的车辆,可以直接通过传感器测量4个独立悬架的悬架挠度(即zi-qi,i ∈{0,1,2,3})、车身俯仰角速度()、车身侧倾角速度()以及质心垂向位移加速度(),然后可以根据可用的测量结果估计所有的系统状态.

为降低整车主动悬架系统状态估计的计算量,根据系统中4个独立悬架与车身姿态之间的关系,将该整车悬架分解为若干耦合的降阶子系统,并根据分解后的子系统设计DMHE算法,其中每个子系统都可以从周围环境中检测相应数据,并通过通信链路从邻居获取与本地子系统估计状态相关的信息.在分解子系统的过程中要满足以下基本原则:

1)为每个子系统至少分配一个仅依赖于相应子系统动态的测量值;

2)子系统的配置不违反系统的物理拓扑;

3)每个分解的子系统是可观测的(即每对(Ci,Ai)都是可观测的).

基于上述原则,整车主动悬架系统具有多种子系统分解方式,考虑到本文状态估计算法中采用的一致性原理需要相应子系统之间具有耦合性,且本地子系统需要在状态估计过程中根据耦合性利用邻居的信息.因此选择其中一种分解方式将整车主动悬架系统分解为5 个耦合的子系统,每个配置的子系统p,p ∈{1,2,3,4},包含关于第p个悬架和车身的状态,并分配测量输出中的第p个测量值,而第5个子系统包含用于表征车身运动升降、侧倾和俯仰等姿态,并分配剩余的3个测量值,并用xi,i ∈{1,2,3,4,5}表示第i个子系统的降阶状态向量,子系统状态向量的配置如表1所示.

表1 整车主动悬架系统子系统状态向量配置Table 1 State vector configuration of full-car activesuspension system subsystems

子系统之间的通信网络用有向图G=(V,E)来描述,其中节点V=1,2,···,m表示传感器,集合E=V×V中的元素即边(j,i)表示传感器j可以向传感器i传递信息.对于每个节点i ∈V,V i表示节点i的邻居集合,即V i{j:(j,i)},其中不包括自环即iV i.用有向图中的V i,i ∈V来表示除第i个子系统外直接影响子系统i状态的子系统指标集.

整车主动悬架分布式结构中的每个子系统可以由以下离散时间状态空间模型描述：

其中:Ci和Di是适当维度的常数矩阵,分别表示第i个子系统测量输出与相应子系统状态和测量噪声的相关性;vi∈R表示子系统i的测量噪声.

将本文描述的子系统通信拓扑与一个随机矩阵K∈RM×M相结合,则其中的元素

所有满足式(5a)-(5c)的矩阵K都与通信网络是兼容的,即给定一个通信拓扑,矩阵K有多种选择以保证状态估计器的收敛性或增加估计的准确性.根据矩阵K,在时刻t时,估计器通过通信链路接收邻居子系统相应信息,即本地子系统i在一个采样间隔内可以利用的测量值为,j ∈V i.

3 主动悬架系统分布式状态估计

对于车辆主动悬架系统式(3)-(4),采用DMHE方法对系统状态进行估计,如图2所示,在每个时刻t,每个节点i ∈V状态的估计都基于本地测量值···,以及从所有邻居节点j ∈V i所获得的t时刻对应的相关状态信息.在提出的分布式估计方案中,每个子系统解决一个MHE问题.首先考虑一个大小为N+1,范围为t-N,t-N+1,···的固定大小的滑动窗口,用表示子系统i在滑动窗口上所收集的所有测量值的向量.所提出的DMHE算法的目标是根据本地子系统在滑动窗口中收集到的测量值和从邻居节点接收的与本地子系统状态相关的信息,以及滑动窗口初始的先验值来进行状态估计.

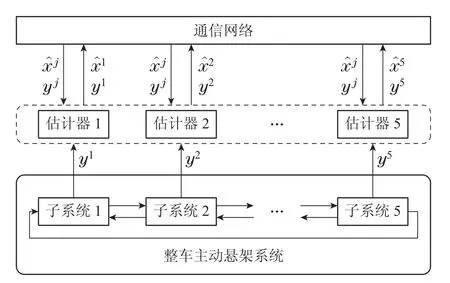
图2 整车主动悬架系统分布式状态估计方案Fig.2 A schematic of distributed state estimation for a fullcar active suspension system

可以将上述约束施加到代价函数最优化求解中.当已知集合为凸集时,约束式(7a)-(7c)可以用线性不等式表示,将式(6)的约束最小化问题转化为可以在实际应用中有效求解的二次规划问题.因此在具有约束的MHE问题中,局部到达代价(·)的选择尤为重要,通常会根据状态估计值与相应先验值的距离进行定义,即

在时间t时,由于分布式结构中的降阶子系统具有耦合关系,因此代价函数式(6)可以自然地拓展到考虑子系统i可能会接收来自邻居节点j ∈V i测量信息的情况,参考文献[19]的相关内容,此时本地子系统i的代价函数可以由式(6)扩展为

针对整车主动悬架系统的分布式结构,引入分布式状态估计中的到达代价一致性原理[20],将本地到达代价和邻居子系统j ∈V i的测量信息,以及相关状态的先验信息进行融合,定义新的局部到达代价(·)为

其中一致性权重ki,i和ki,j是严格正的且满足式(5a)-(5c),以保证融合后新的到达代价是本地到达代价与邻居相关状态到达代价的加权平均值.将K定义为一致性矩阵,等式(10)相当于对局部到达代价执行了一次离散时间的一致性步骤,条件式(5c)可以确保一致性矩阵K是行随机的.

在每个采样间隔中,本地子系统与邻居可能进行多次通信即信息传递,这相当于在一个采样间隔时刻进行多次(如L次)信息融合,令l=1,···,L,根据式(10)扩展该一致性融合算法,即

通过对相应的向量和矩阵以及权重参数执行一致性算法,将其应用于整车主动悬架系统,采用分布式结构,通过以下算法执行一致性步骤,以求用更少的计算量获得同样的效果.

引理1令l=1,···,L,给定如下一致性算法:

则融合后的局部到达代价式(11)等价为

对局部到达代价执行一致性步骤后的融合到达代价可以表示为

可以看出式(16)和式(17)的推导中关于xi的项都是相同的,因此使用式(16)或式(17)作为到达代价会在滑动窗口上得到相同的估计值证毕.

综上,在整车主动悬架系统状态的估计中,本文采用的DMHE算法将整个悬架系统分解为多个耦合的降阶子系统,考虑到子系统状态之间的相关性,提出一种基于一致性的分布式状态估计算法,采用MHE方法来处理系统状态和过程干扰的约束(如物理约束等),具体算法步骤如下:

步骤1在初始时间t0时,子系统的估计器用先验估计,本地及邻居子系统测量值,i ∈V和邻居子系统的先验估计值,j ∈V i来初始化;

步骤2时间t>0 时,使用式(15)初始化 式(12)-(13),执行L次的一致性算法;

步骤3在式(7a)-(7c)的约束下,通过最小化带有式(14)形式到达代价的目标代价函数式(9)来得到本地子系统i的估计值

步骤4通过递推得到下一时刻子系统i的先验值,以及目标代价函数中对应的权重矩阵

4 稳定性分析

在采用DMHE算法进行估计的过程中必须研究稳定性,因为在每个时域窗口都只使用了整个数据的一个子集求得近似结果.其中对于系统的主要设置是估计问题的约束,如果系统约束的选择不当就会使得系统误差无法保持动态稳定,估计值无法收敛到真实状态.因此对具有约束的主动悬架DMHE算法的稳定性问题进行分析尤为重要.

定义1[19]如果可观性矩阵(Ai,Ci)是可观的,则系统可由传感器i局部观测,即传感器i是局部可观的,即系统是整体可观的.

Di为适当维数的单位矩阵,Hi和Mi为分块托普利兹矩阵.

考虑条件式(5a)-(5c),系统的一致性矩阵K是行随机的,即该方阵的行和都等于1.根据Perron-Frobenius定理,存在一个向量p具有严格的正交分量pi,i ∈V且满足等式pTKL=pT,即其中表示矩阵KL的第(j,i)个元素.

在稳定性分析过程中,首先确定目标函数的上下界.在稳定性推导中令可以使推导过程更加直观,从系统状态估计的稳定性方面来看这两个到达代价的选择是等价的.

即目标代价函数上界为

根据代价函数式(9)以及系统状态空间方程,将局部到达代价进行改写可得

用同样的原理可以得到不等式

参考系统模型式(3)-(4)以及矩阵Φi和Ψi,根据与系统的卡尔曼滤波相关联的差分Riccati方程进行迭代可得矩阵Λi,即

然后结合式(24)-(25)可得

即最优化代价函数下界为

证毕.

定理1子系统i的状态先验估计以及权重矩阵可通过迭代给出

证根据等式(28)可得

根据等式(29)可得

结合系统误差的李雅普诺夫候选函数(27)可得

根据不等式(30)可以看出,在时间t趋向于无穷时,系统误差动态的李雅普诺夫函数Vt(et-N)是有界的.在集体可观测性和网络连通性的条件下,Vt(et-N)的有界性包含了每个网络节点即主动悬架子系统估计误差的有界性,从而完成了稳定性分析.证毕.

5 仿真验证与分析

考虑整车主动悬架系统模型(1)参数值如表2所示,4个独立悬架的控制输入分别由以下函数以周期Ts=0.04 s的采样间隔产生:

表2 整车主动悬架系统的变量参数Table 2 Variables of full-car active suspension systems

同时考虑悬架的有界未知噪声(即车辆行驶过程中路面不平整引起的扰动),假设该随机噪声服从高斯分布,且噪声的大小不超过10-2m,在估计过程中局部估计器采用MHE的方法处理噪声的约束.整车主动悬架系统的初始状态设置为q1(t0)=-0.02 m,q2(t0)=-0.02 m,q3(t0)=0.02 m,q4(t0)=0.02 m,z(t0)=0 m,θ(t0)=0.04◦,ϕ(t0)=0.02◦,其中由测量输出组成的系统输出向量为

仿真实验使用MATLAB R2016a 软件,主机中央处理器Inter(R)Core(TM)i7-10700 KF,主频3.8 GHz,图形处理器配置为GeForce RTX 3080.在仿真中,取滚动时域步长为4,图3和图4分别给出了4个独立悬架状态的实际值、估计值和估计误差,图5-7分别是车身升降、俯仰和侧倾状态的真实值、估计值和估计误差.仿真结果显示算法的估计状态都较为精准地跟踪了悬架位移、车辆姿态等系统相关状态,且所有状态的估计误差保持在一个较小的范围内.

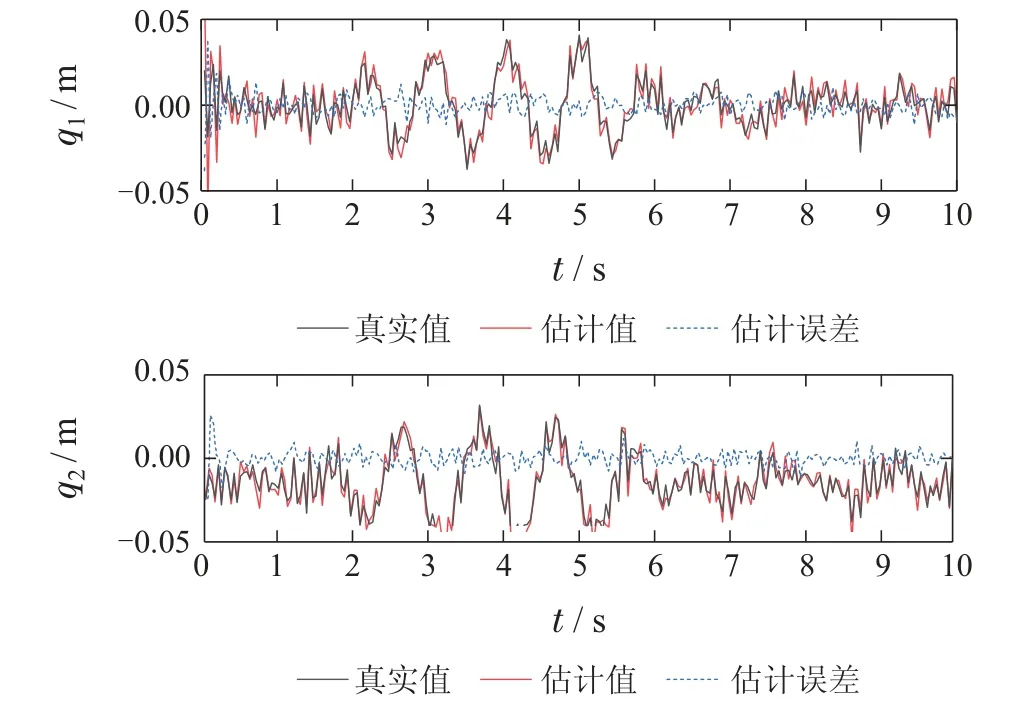
图3 悬架1和2的非簧载质量位移估计结果Fig.3 Estimation results of unsprung mass displacement of suspension 1 and 2

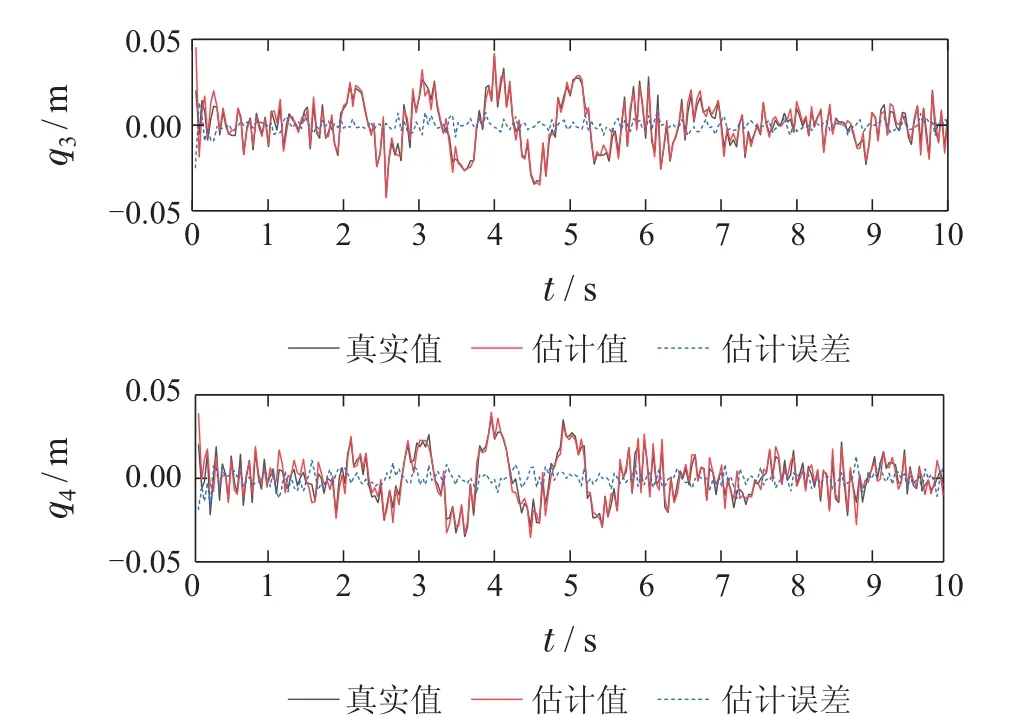
图4 悬架3和4的非簧载质量位移估计结果Fig.4 Estimation results of unsprung mass displacement of suspension 3 and 4

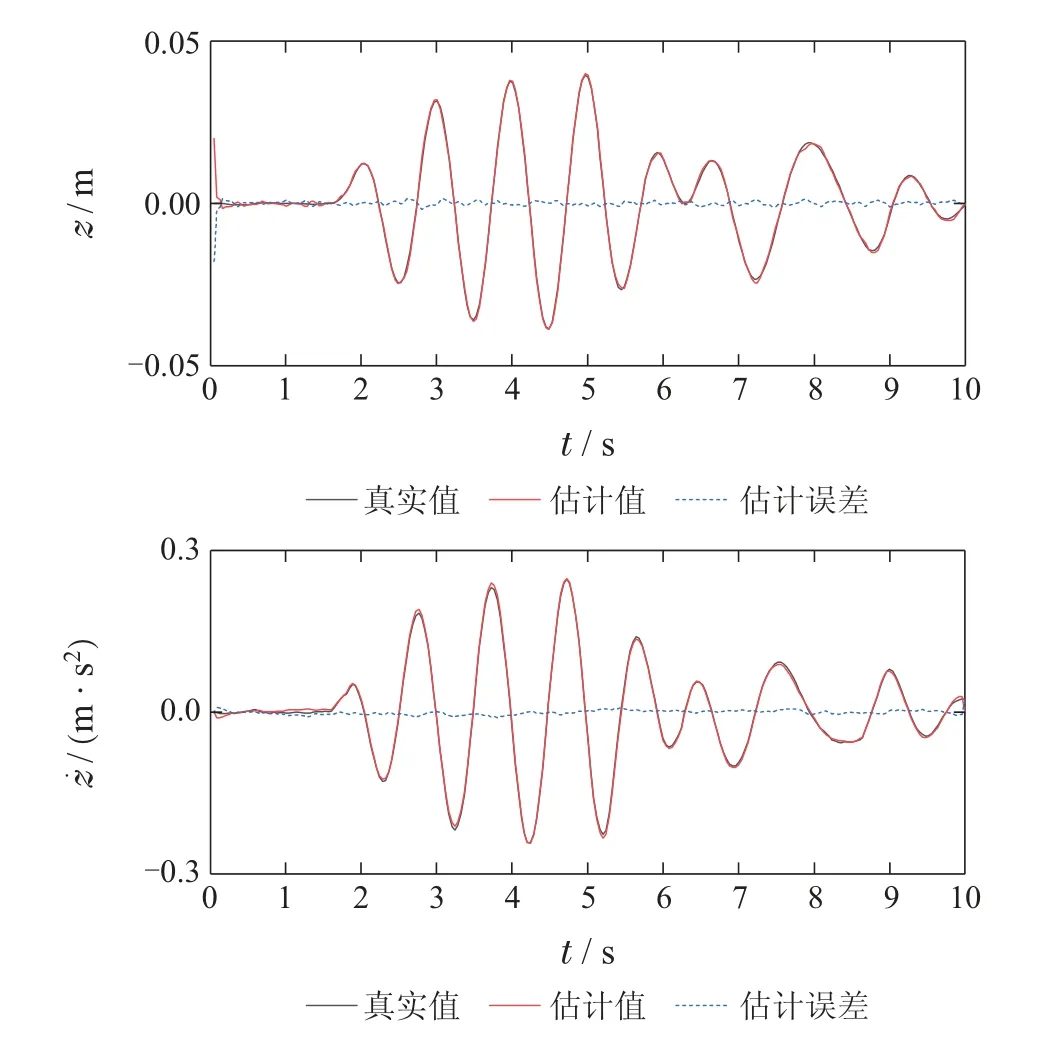
图5 车辆升降姿态估计结果Fig.5 Vehicle attitude estimation results

图6 车辆侧倾姿态估计结果Fig.6 Vehicle roll attitude estimation results

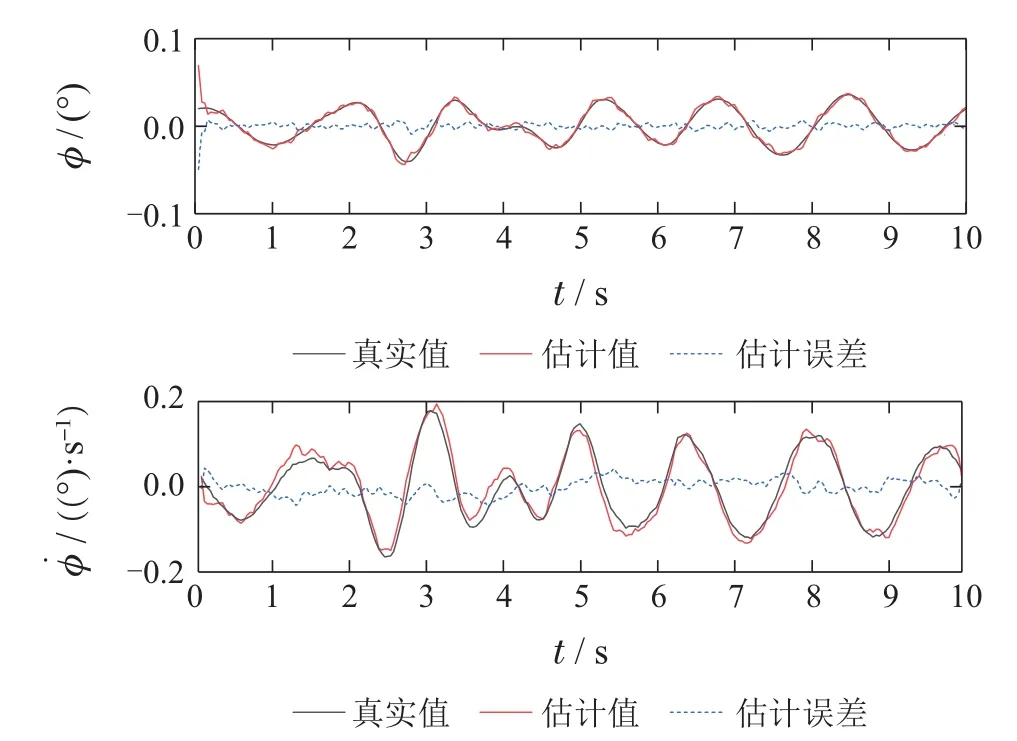
图7 车辆俯仰姿态估计结果Fig.7 Estimation results of vehicle pitching attitude

在分散式MHE[21]和集中式MHE[22]方法的基础上,在同样的环境下对整车主动悬架系统进行了另外两组仿真,如图8所示对这3种估计方案进行了性能比较分析.采用归一化估计误差范数作为性能指标,图8给出了3种估计方案的归一化估计误差的图像.可以看出与现有的分散式MHE方案相比,分布式MHE方案估计误差要小很多,并且其估计精度与集中式MHE方案相当.

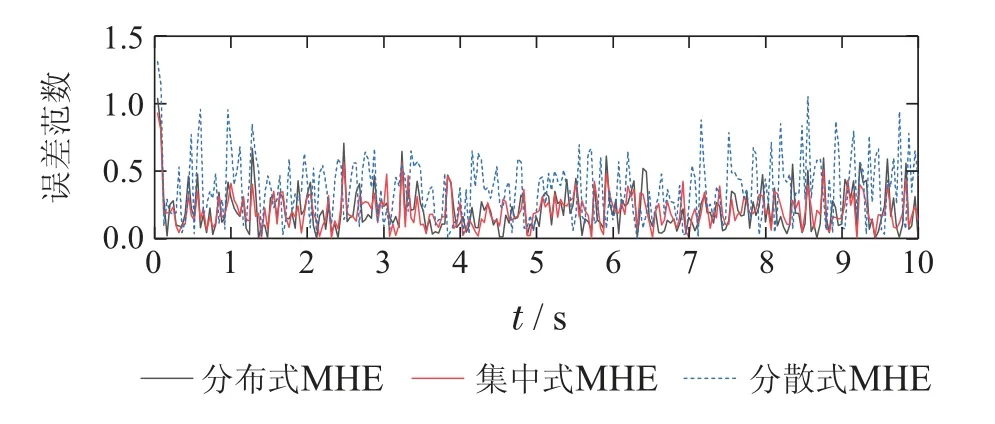
图8 不同估计方案的估计误差范数Fig.8 Estimation error norm of different estimation schemes

表3给出了本文及其对比估计方案的归一化估计误差范数的平均值,同时给出了4种估计方案估计的平均计算时间.在计算不同估计方案的估计误差时考虑了整车主动悬架的全部状态,以确保误差范数对比的公平性.

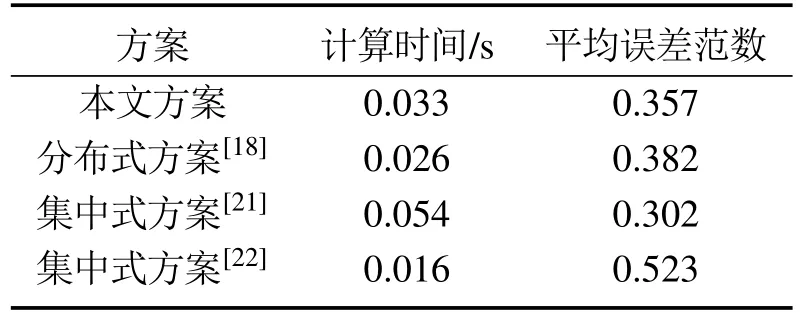
表3 不同估计方案的计算时间和归一化误差范数Table 3 Calculation time and normalized error norm of different estimation schemes

由表3可以看出,提出的分布式估计方案几乎与集中式方案效果相当,但与集中式方案相比,节省了约38.89%的计算时间.考虑到车载嵌入式平台的计算能力限制及悬架系统状态变化的快速性,本文方案距离在线实时估计仍有一定距离,但计算时间的降低对于在线估计能力的提升非常有利,而与分散式方案相比,估计精度提高了26.34%.进一步与文献[18]估计方案相比,虽然估计时间略有增加,但估计精度提高了6.53%,验证了所提出估计算法的有效性.

6 结语

本文提出了一种整车主动悬架分布式一致性滚动时域估计方法,求解车辆在随机路面激励情况下行驶时主动悬架的状态估计问题.先考虑一个具有七自由度的整车主动悬架动力学模型,根据可用的测量结果和系统状态建立状态空间方程,并将整车主动悬架系统分解为若干个耦合的降阶子系统.进一步,本地子系统根据邻居子系统的信息,利用到达代价一致性原理扩展代价函数,并通过最优化代价函数对整车主动悬架系统的状态进行估计.仿真结果表明: 本文方法在有效降低估计计算量的同时能够处理车辆主动悬架在行驶过程中存在的路面随机激励和测量噪声,对车辆主动悬架系统的状态进行准确的估计.当悬架模型是由可变特性的弹簧和减震器构成的半主动悬架即不涉及独立悬架的控制输入,该估计算法同样适用.后续将在本文结果基础上,研究整车主动悬架系统分布式一致性滚动时域估计的快速计算方法和在不可靠通信下的状态估计策略.