网络化不确定系统集中式融合鲁棒稳态估值器
2023-10-04陶贵丽刘文强
陶贵丽,李 爽,刘文强
(1.浙江传媒学院媒体工程学院,浙江杭州 310018;2.浙江工商大学信息与电子工程学院(萨塞克斯人工智能学院),浙江杭州 310018)
1 引言
多传感器信息融合技术可以利用所有传感器的信息,克服了单传感器受时间和空间限制的缺陷,现已被广泛应用于目标跟踪、导航制导、信号处理等热门领域[1].
近年来,网络化系统的滤波问题受到广泛关注[2-4].众所周知,经典Kalman滤波方法要求系统的模型参数和噪声方差是精确已知的[5],但在实际应用中,由于建模误差或未建模动态以及随机扰动等原因,导致系统模型是不确定的[6-17].当系统模型中存在不确定性时,Kalman滤波器的性能会严重变坏,甚至导致滤波发散.解决这一问题的方法之一是设计鲁棒Kalman滤波器,即针对由不确定性所描述的一族系统模型来设计一个滤波器,使得对所有容许的不确定性,滤波器的实际滤波误差方差确保有一个最小上界[17].
在网络化系统中,信道中会不可避免地存在不确定性,例如随机观测滞后与丢包,估值器的性能会受其影响[18].这类不确定性的存在会导致估值器接收到的数据出现偏差.伯努利随机变量序列是描述这类不确定性的常用工具[19-21].
随机参数不确定性可以用乘性噪声来描述,对确定性参数的随机扰动称为乘性噪声,包括状态依赖和噪声依赖乘性噪声.在系统状态和观测矩阵中的白噪声称为状态依赖乘性噪声,在噪声转移矩阵中的白噪声称为噪声依赖乘性噪声.噪声方差的不确定性可以通过确定的不确定性来描述,即噪声方差是未知不确定的,但有已知的保守上界[14-17].近年来,对于带乘性噪声、不确定噪声方差、随机观测滞后和丢包的网络化系统,鲁棒或最优状态估计问题已被广泛研究[15-17,22-28].文献[22]中,针对系统状态和观测矩阵中带乘性噪声并具有多步随机观测滞后和丢包的不确定网络化系统,通过射影理论,提出了最小方差意义下的最优线性估值器.文献[23]中,针对带乘性噪声、一步随机观测滞后和丢包的网络化控制系统,其中传感器到估值器和控制器到执行器的通道都受到乘性噪声影响,利用射影理论推导出了最优估值器.但文献[22-23]的结果都局限于单传感器系统.
对于在系统状态和观测矩阵中带乘性噪声,并具有一步随机传输时滞和丢包的混合不确定多传感器网络化系统,文献[24]基于矩阵加权融合算法提出了一种分布式融合滤波器.对于一类在状态转移矩阵中存在乘性噪声,并具有丢失观测、随机观测滞后和丢包的不确定多传感器网络化系统,应用新息分析方法,文献[25]提出了鲁棒集中式融合以及降维观测融合Kalman滤波器,但文献[25]没有考虑系统观测矩阵中的乘性噪声.文献[26]中,针对带随机参数矩阵、一步随机观测滞后和丢包的多传感器网络化系统,提出了局部最小二乘线性估值器(滤波器和固定点平滑器),并利用矩阵加权融合算法得到了分布式融合滤波器和平滑器.然而,文献[22-26]均没有考虑噪声依赖乘性噪声,且都假定系统噪声方差是精确已知的.
针对在系统状态和观测矩阵中带乘性噪声,并带丢包和不确定噪声方差的多传感器网络化系统,文献[27]提出了加权状态融合鲁棒Kalman估值器.但文献[27]中没有考虑随机观测滞后不确定性.对系统状态和观测矩阵中存在乘性噪声,并具有一步随机观测滞后和不确定噪声方差的多传感器网络化系统,文献[28]提出了综合协方差交叉融合鲁棒Kalman估值器.文献[15]针对在系统状态与观测矩阵中存在相同乘性噪声,以及带一步随机观测滞后、丢失观测、以及不确定噪声方差的多传感器网络化系统,利用极大极小鲁棒估计准则,提出了鲁棒矩阵加权和集中式融合稳态Kalman估值器.文献[16]中,针对带乘性噪声、两步随机观测滞后、丢失观测和不确定噪声方差的多传感器网络化系统,提出了鲁棒集中式融合和加权观测融合稳态Kalman估值器.文献[15-16]提出的鲁棒融合滤波方法可用于解决带有色观测噪声的多传感器单通道自回归信号的鲁棒融合滤波问题.但文献[15-16,27-28]中均没有考虑噪声依赖乘性噪声.对于系统状态和过程噪声转移矩阵中带乘性噪声,并具有不确定噪声方差、一步随机观测滞后和丢失观测的多传感器网络化系统,文献[29]提出了鲁棒局部和5种融合时变Kalman估值器(预报器、滤波器和平滑器).但文献[29]中没有考虑系统观测矩阵中的乘性噪声,且文献[15-16,28-29]都没有考虑丢包.此外,与文献[15-16]相比,文献[28-29]中用到的增广方法会使系统状态转移矩阵具有较大维数.对一类系统所有参数矩阵中带相同乘性噪声,并带一步随机观测滞后和不连续丢包的多传感器网络化系统,根据极大极小鲁棒估计原理,文献[17]提出了鲁棒矩阵加权融合稳态Kalman估值器.但文献[17]中没有考虑丢包补偿机制以及集中式融合滤波问题.基于上述分析,对于在系统状态和观测矩阵中带相同状态依赖乘性噪声,并带噪声依赖乘性噪声、不确定噪声方差、一步随机观测滞后和丢包的多传感器网络化系统,其鲁棒集中式融合稳态滤波问题尚未见报道.因此,本文对此进行研究.
本文的主要创新点如下: 1)对于所研究的系统模型,给出了其集中式融合鲁棒稳态估值器存在的充分条件,并基于极大极小鲁棒估计原理提出了集中式融合鲁棒稳态Kalman估值器(预报器、滤波器和平滑器);2)应用增广方法、非负定矩阵分解方法和李雅普诺夫方程方法,证明了所提出的集中式融合估值器的鲁棒性;3)给出了一个应用于多传感器多通道滑动平均(moving average,MA)信号估计的例子,解决了带随机参数矩阵的多通道MA信号的集中式融合估计问题,得到了相应的鲁棒局部和集中式融合稳态信号估值器.
2 问题描述
考虑如下线性离散不确定多传感器网络化系统:
其中:t是离散时间;x(t)∈Rn是被估状态;zi(t)∈Rmi是传感器接收到的观测;yi(t)∈Rmi是估值器接收到的观测;w(t)∈Rr是过程噪声;vi(t)∈Rmi是观测噪声且线性相关于w(t);αk(t)∈R1,k=1,···,nα是状态依赖乘性噪声;βk(t)∈R1,k=1,···,nβ是噪声依赖乘性噪声;Φ∈Rn×n,Φk∈Rn×n,Γ∈Rn×r,Γk∈Rn×r,Hi∈Rmi×n,Hik∈Rmi×n和Di∈Rmi×r是具有适当维数的已知常矩阵;Φk,Γk和Hik是扰动方位矩阵;nα,nβ是相应乘性噪声的数目;L是传感器的数目.
ξi(t)∈R1和ζi(t)∈R1,i=1,···,L是取值为0或1的各自不相关伯努利白噪声,具有已知概率Prob(ξi(t)=1)=πi,Prob(ξi(t)=0)=1-πi,Prob(ζi(t)=1)=ςi,Prob(ζi(t)=0)=1-ςi,其中πi和ςi是已知的,且0 ≤πi≤1,0 ≤ςi≤1.ξi(t)和ζi(t)也不相关于其他随机信号.容易得到以下结论:
假设1w(t),ηi(t),αk(t)和βk(t)是具有零均值的互不相关白噪声,它们的协方差为
注2在式(4)中,白噪声ξi(t)和ζi(t)被用来描述一步随机观测滞后和丢包.如果ξi(t)=1,则yi(t)=zi(t)(没有观测滞后和丢包);如果ξi(t)=0且ζi(t)=1,则yi(t)=zi(t-1)(一步随机观测滞后);如果ξi(t)=0 且ζi(t)=0,则yi(t)=yi(t-1)(丢包),即观测zi(t)丢失,但估值器在t-1时刻接收到的观测yi(t-1)被用来作为t时刻的补偿,这称为保持输入补偿机制.这不同于文献[17]中的零输入补偿机制,即如果当前时刻传感器观测丢失,则估值器的观测将被置为0.
3 模型转换
3.1 增广集中式融合系统
合并式(2)给出的所有传感器输出向量,得到如下增广观测输出方程:
将式(2)代入式(4)中,然后合并所有由式(4)给出的估值器收到的观测向量可得
应用式(1)(7)-(8)可得如下增广集中式融合系统:
增广集中式融合系统(9)-(10)可进一步被转化为带常参数矩阵和乘性噪声的系统形式,即
此外,利用式(5)可得
容易证得ξiz(t),ζiz(t)和γiz(t)是互不相关的白噪声.
注3相比于文献[28-29],由式(11)给出的增广状态xa(t)具有较小的维数,如果采用文献[28-29]中的方法,增广状态的维数为2n+2m,而式(11)给出的增广状态xa(t)的维数仅为n+2m.可见,本文方法可减少计算量.
3.2 实际和保守状态二次非中心距
由式(12)可得xa(t)的保守二次非中心距为
引理2在假设3条件下,可得
证完全类似于文献[15]中引理5的证明,容易证得引理2成立.证毕.
证如果ρ()<1,则类似于文献[24,31]中的证明过程,通过直接应用文献[32-33]中的结果可证明引理3成立.证毕.
3.3 虚拟过程和观测噪声
增广状态方程(12)可被改写为
其中wf(t)是虚拟过程噪声,
容易证得wf(t)是零均值白噪声,且它的保守稳态方差为
增广集中式融合观测方程(13)可被改写为
其中vf(t)是零均值虚拟观测白噪声,且vf(t)可表示为
虚拟噪声wf(t)和vf(t)的保守稳态相关矩阵为
4 鲁棒集中式融合稳态Kalman估值器
4.1 鲁棒集中式融合稳态Kalman预报器
对于由式(20)(23)给出的带已知保守噪声统计Qf,Rf和Sf的最坏情形时不变集中式融合系统,在假设1-4条件下,基于极大极小鲁棒估计原理[30],应用标准Kalman滤波算法[5],可得保守最优集中式融合稳态一步Kalman预报器为
应用式(31)可得保守集中式融合稳态Kalman一步预报误差方差,也满足如下李雅普诺夫方程:
引理4[30]令Λ≥0,Λ∈Rr×r,设Λδ=(Λij)rL×rL,Λij=Λ,i,j=1,···,L,则Λδ≥0.
引理5在假设3条件下,可得如下矩阵不等式关系:≤Λf.
证明过程详见附录A.
引理6[34]考虑如下李雅普诺夫方程:U=CUCT+V,其中:U,C和V是n×n矩阵,V是对称矩阵,C是稳定矩阵(即它的所有特征值都在单位圆内).如果V≥0,则U是对称并唯一的,且U≥0.
定理1在假设1-4条件下,由式(27)给出的实际集中式融合稳态Kalman预报器具有鲁棒性,即对于所有容许的不确定性,实际预报误差方差满足如下关系:
证明过程详见附录B.
由式(27)给出的实际融合稳态Kalman预报器为鲁棒融合稳态Kalman预报器,由式(34)给出的矩阵不等式关系称为它的鲁棒性.
4.2 鲁棒集中式融合稳态Kalman滤波器和平滑器
利用式(38)可得保守稳态估计误差方差为
定理2在假设1-4条件下,由式(35)给出的实际集中式融合稳态Kalman滤波器和平滑器具有鲁棒性,即对于所有容许的不确定性,相应的所有实际估计误差方差满足如下关系:
证明过程详见附录C.
由式(35)给出的实际集中式融合稳态Kalman滤波器和平滑器被称为鲁棒集中式融合稳态Kalman滤波器和平滑器,由式(40)给出的矩阵不等式关系称为它们的鲁棒性.
且P(c)(N)是(c)(N)的最小上界.
推论2 完全类似于式(9)-(43)的推导,容易得到原始系统(1)-(4)的鲁棒局部稳态Kalman 估值器(t|t+N),N=-1,N≥0,i=1,···,L,且它们的实际估计误差方差(N)有相应的最小上界Pi(N),即
注5利用射影理论可以证得
注6在注5中,被称为相应鲁棒Kalman估值器的实际精度,trP(c)(N)和trPi(N)被称为鲁棒精度(或者全局精度).迹的值越小意味着精度越高.注5表明,估值器的实际精度都高于或等于它的鲁棒精度,鲁棒精度是最低的实际精度.集中式融合器的鲁棒精度高于各局部估值器.
5 带有色观测噪声和混合不确定性的多通道MA信号估计应用实例
自回归滑动平均(autoregressive MA,ARMA)信号滤波问题经常发生在信号处理、状态估计、目标跟踪、反卷积以及时间序列分析等领域.考虑如下带有色观测噪声和混合不确定性的多传感器多通道MA信号:
目的是为多传感器多通道MA信号s(t)设计鲁棒集中式融合稳态Kalman估值器.
由式(53)-(54)可得
带随机参数矩阵的多通道MA信号模型(49)可被转换为如下等价的状态空间模型[5]:
将Bk(t)=Bk+Υk(t)代入Γs(t),并应用式(56)得
有色观测噪声r(t)有等价的状态空间模型为[5]
将Ak(t)=Ak+Λk(t)代入Φr(t)和Hr(t),并应用式(56)得
这里Φrk,k=1,···,p是m×mp矩阵,它的第(1,k)个块矩阵为单位矩阵Im,其余位置均为(0)m×m.Hrk,k=1,···,p是m×mp矩阵,它的第(1,k)个块矩阵为-Im,其余位置均为(0)m×m.
于是可得如下增广系统模型:
应用式(59)和式(62)可将增广系统(63)-(65)转换为如下带常参数的系统:
因此,应用状态空间方法和增广方法,多通道MA信号模型(49)-(54)被转换成带乘性噪声、一步随机观测时滞、丢包和不确定噪声方差的状态空间模型式(52)(66)-(68).
由式(58)可得s(t)=[Hs(0)m×mp]x(t),于是,鲁棒融合信号估计问题可以通过鲁棒融合状态估计来解决,应用射影理论[5]可得
信号s(t)的实际和保守集中式融合稳态估计误差方差分别为
这里,上角标“s”表示信号.
注7对系统(52)(66)-(68),当取m=1时,MA信号s(t)是单通道信号,此时系统(52)(66)-(68)可视为系统(1)-(4)的一种特殊情况,其中:
6 仿真实例
由于信号s(t)∈R1,所以估计误差方差的迹值等于相应的估计误差方差值.表1给出了实际和保守局部与集中式融合稳态估计误差方差的比较,这验证了由式(43)-(46)给出的稳态精度关系.表1中N=-1表示预报器,N=0表示滤波器,N=1 表示一步平滑器,N=2表示两步平滑器.
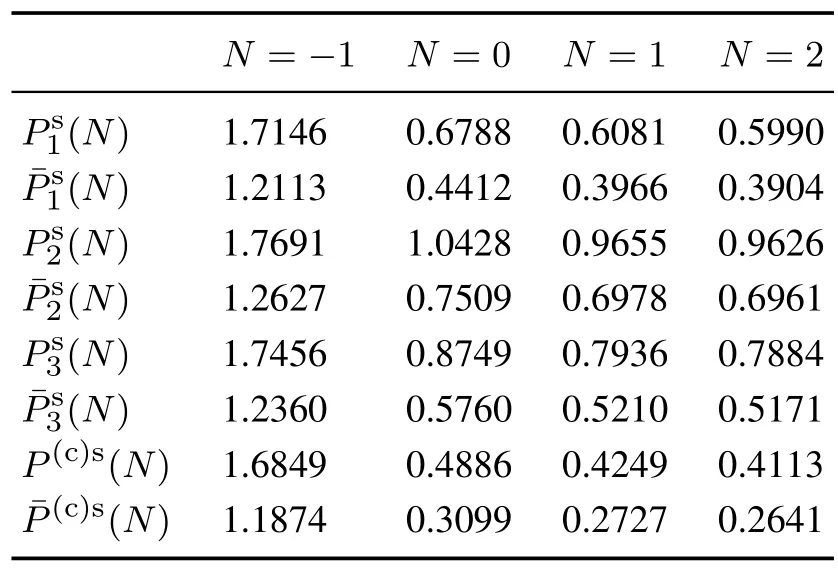
表1 信号s(t)的稳态鲁棒和实际精度比较Table 1 Comparison of steady-state robustness and actual accuracy of signal s(t)
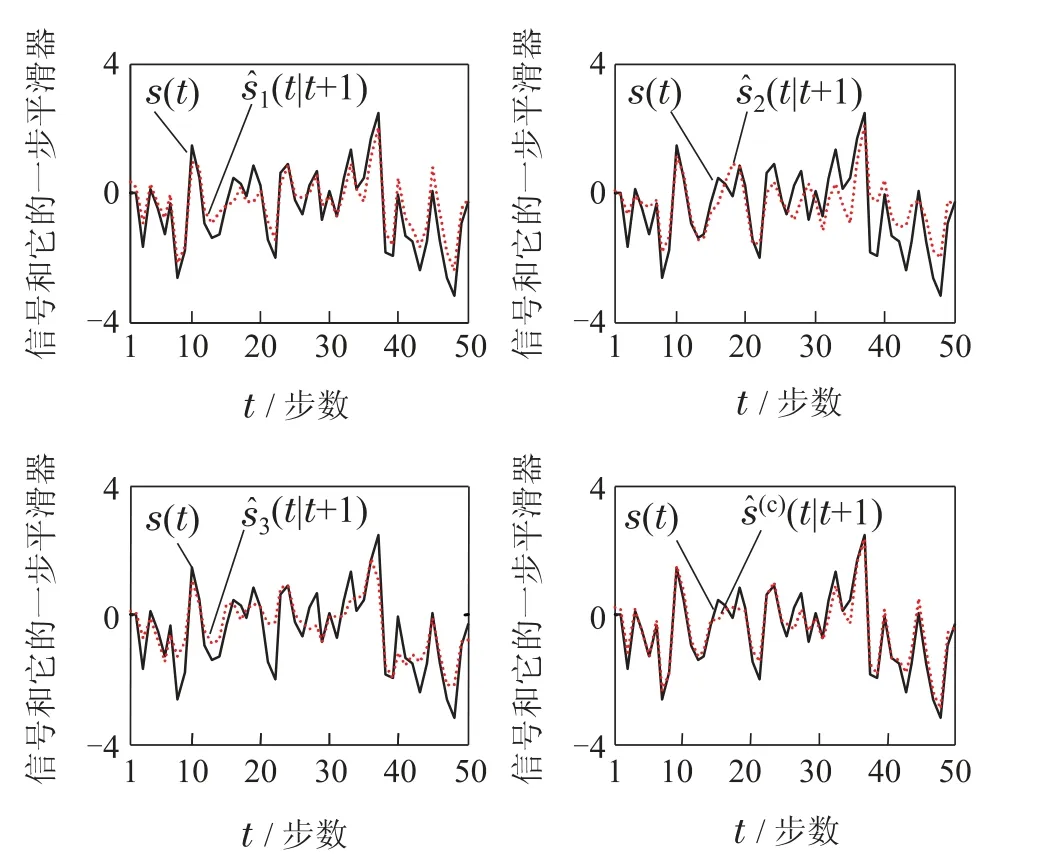
图1 信号s(t)和它的实际局部和集中式融合一步平滑器Fig.1 Signal s(t)and its actual local and centralized fusion one-step smoothers
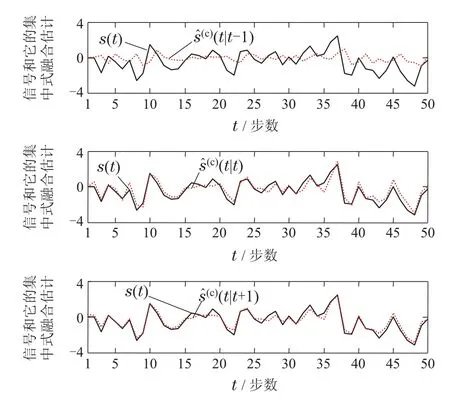
图2 信号s(t)和它的集中式融合估值器Fig.2 Signal s(t)and its centralized fusion estimator
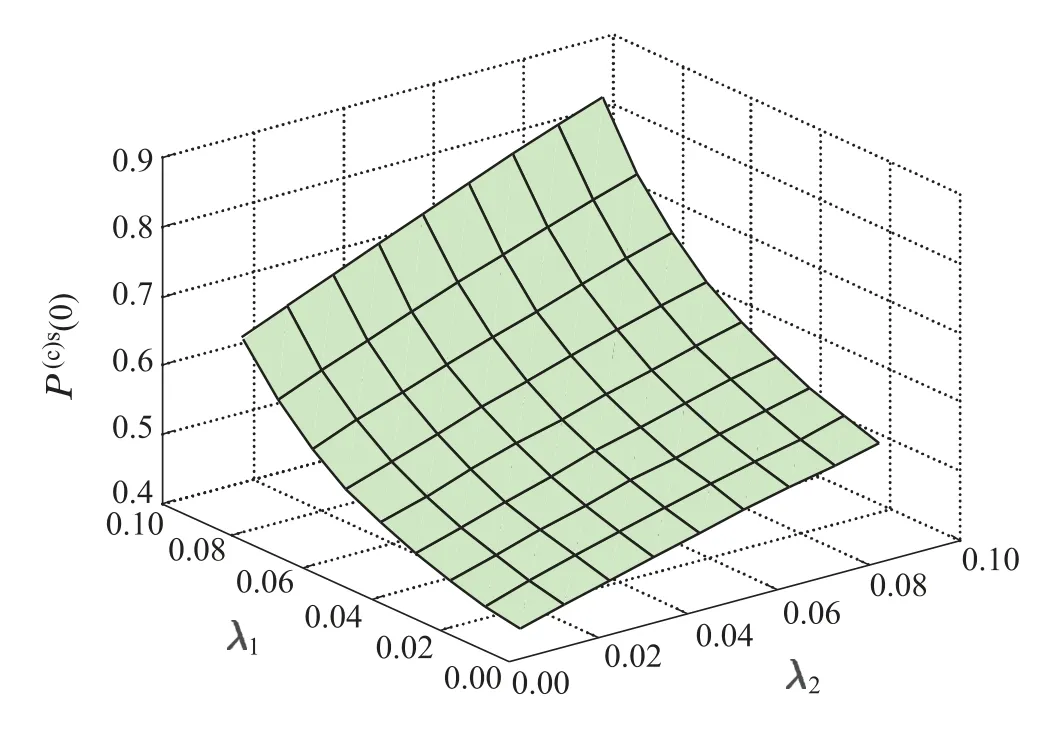
图3 P(c)s(0)随着λ1和λ2增加时的变化情况Fig.3 Changes of P(c)s(0)with the increase of λ1 and λ2
7 结论
针对在系统状态转移矩阵和观测矩阵中带相同状态依赖乘性噪声,并带噪声依赖乘性噪声、不确定噪声方差、一步随机观测滞后和丢包的多传感器网络化系统,应用增广方法、去随机化方法和虚拟噪声技术将该系统转换为仅带不确定噪声方差的集中式融合系统.转换之后系统的过程噪声和观测噪声是相同的,这可避免求解它们的相关矩阵.根据极大极小鲁棒估计原理,提出了鲁棒集中式融合稳态Kalman估值器(预报器、滤波器和平滑器).应用增广噪声方法、非负定矩阵分解方法和李雅普诺夫方程方法,证明了估值器的鲁棒性.所提出的方法可用于解决带随机参数矩阵、不确定噪声方差和网络化随机不确定性的多传感器多通道MA信号的鲁棒融合Kalman滤波问题.仿真实验证明了所提出方法的可应用性与正确性.
附录A
附录B
附录C
