机械传动振动信号IFDM+1DRCAE组合方法处理及诊断
2023-10-03青海高等职业技术学院机电工程系青海海东市810799李有新
(青海高等职业技术学院,机电工程系,青海海东市,810799) 李有新
当机械设备发生振动时,由于实际转速、摩擦作用与载荷条件都会发生改变,从而形成不稳定的信号特征[1]。虽然可以利用傅里叶方法实现频谱信号的准确分析,但采用该方法只能满足线性以及平稳信号分析要求,对于不稳定的非线性信号则存在明显局限性[2]。针对以上情况,有学者综合运用短时傅里叶转换、小波变换等方法对设备使用阶段产生的机械故障进行诊断分析[3]。EMD从局部特征时间尺度层面考虑,对瞬时频率进行单分量分析,经过多次迭代与筛分处理后使非线性以及非平稳信号进行分解得到包含本征模态函数(IMF)与参数变化趋势的集合,由此完成包络谱以及时频分析功能[4-5]。
针对EMD 自适应与瞬时频率的单分量物理意义,本文为实现采用快速傅里叶变换(FFT)方法对非线性与非平稳信号进行分析的功能,设计了一种新的自适应傅里叶分解(IFDM)方法。
1 方法
1.1 改进傅里叶分解方法(IFDM)
采用IFDM方法进行处理的目标是根据快速傅里叶变换过程,把包含一定能量的非线性与非平稳信号自主分解成包含瞬时频率的不同单分量信号,计算式如下[6]:
式中:yi(t)表示FIMF分量,n(t)代表噪声、剩余信号与变化趋势,同时分解过程需满足正交性、完备性、局部性与自适应性要求。
对非线性与非平稳均值为0 的信号x(t)(t∈[t0,t0+T])进行判断,当符合傅里叶变换Dirichlet 条件时,按照Bk[fk-1,fk)=区间完成信号的逆快速傅里叶转换:
由此得到以下形式的原信号:
离散化为:
应对IFDM方法的以下三个方面进行分析。利用快速傅里叶转换方法进行处理时会方式信号幅度的明显辩护啊,同时也无法保持恒定的频率状态,对计算展开过程造成了一定的干扰,因此需对该方法进行优化调整,但上述分析只考虑频率恒定的条件,并未加入时间因素的影响。IFDM 属于一个局部概念,包含了恒定的基函数,因此可以将所有函数都通过傅里叶正交基空间进行展开,并且基函数也会发生变化,完成基函数的自适应重构过程。同时还应注意IFDM方法要达到完备性以及正交性要求。考虑到自适应重构区间并集包含了完整的频谱,存在明确的基函数空间,对其进行重构也不会引起能量损耗,从而可以完整进行分解。
1.2 故障诊断流程
从图1中可以看到根据1DRCAE进行故障诊断的各项流程,可将其分成离线与在线两种基本形式。进行离线训练的时候,通过训练数据完成特征提取器与分类器的训练;进行在线测试时,利用网络完成输入数据的分类预测,之后输出相应的标签。
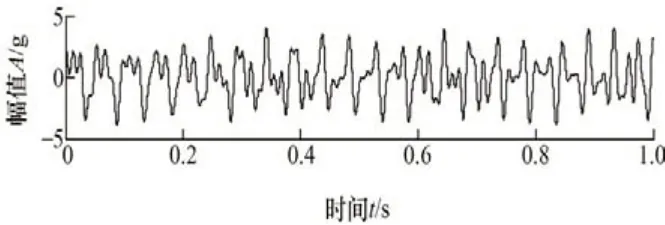
图2 仿真信号x(t)时域波形
2 仿真信号分析
为了对IFDM进行有效性测试,先对式(4)模拟信号进行分析。
x(t)包含了经过调幅调频处理的时变模态信号,得到图1中的x(t)时域波形。
依次通过EMD、IFDM 各方法分解x(t)。通过EMD 分解获得的各IMF 分量都存在明显的模态混叠情况,跟实际分量存在明显差异;以IFDM获得的3个IMF分量依次与1x(t)、2x(t)、3x(t)存在关联性。通过FDM分解生成的第2与第3个IMF相对实际分量在两端点位置形成了明显误差。经对比可知,IFDM达到了最佳分解效果。为实现量化比较的目标,表1 为分别以各分解方法处理得到的正交性指标(IO)。表1 显示,IFDM 分解方法都形成了接近0的分量正交指标,其中,以EMD 方式获得了较大正交性指标,此时IMF 分量发生了模态混叠的现象;从计算耗时层面考虑,EMD需对非线性约束优化过程进行分析,实际处理数据量较大,耗费大量时间;IFDM 方法只进行HHT 与逆快速傅里叶转换,在所有分解方法中耗时最短;之后测试了IMF分量和真实分量之间的相关性,同时发现,以IFDM方法获得的FIMF 分量也跟x(t)的对应成分x1(t)、x2(t)、x3(t)也显著相关性。根据以上研究结果可知,相对EMD 处理方式,以IFDM 获得的IMF 分量表现出了更优的正交性、更短计算时间以及更高的精度。
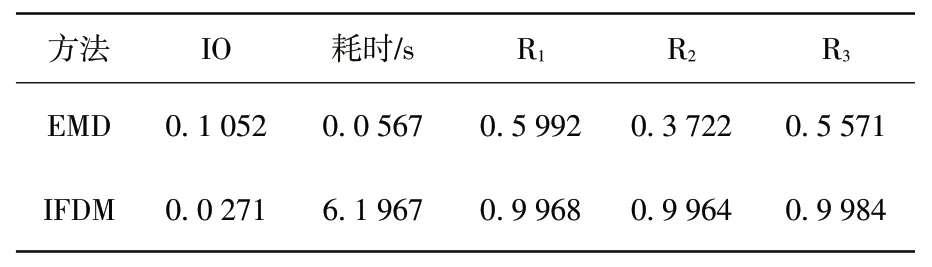
表1 x(t)的评价指标对比
以上模拟信号x(t)包含了3个具有时变特征的模态,同时考虑由恒定频率组成的模拟信号
y(t)包含2 个固定频率调幅信号及1 个余弦信号。
依次通过EMD、IFDM方法分解y(t),设定EMD的模态数量为3,同时将惩罚参数设置为α=1000。从表2中可以看到分别采用各分解方法进行处理得到的正交指标,再利用相关系数法分析计算耗时与模态的关系。对图4进行分析可知,通过EMD计算获得的3 个IMF 相对真实分量形成了较大的误差,采用IFDM计算出的IMF分量则跟真实分量之间形成了较小绝对误差,其中,以IFDM方法处理时形成了比EMD更明显的端点效应。综合考虑正交性、相关性、计算耗时情况,IFDM依然具备较大优势。根据本次分析结果可知,EMD虽然可以满足模态混叠信号分解功能,但依然未达到IFDM的分解性能。
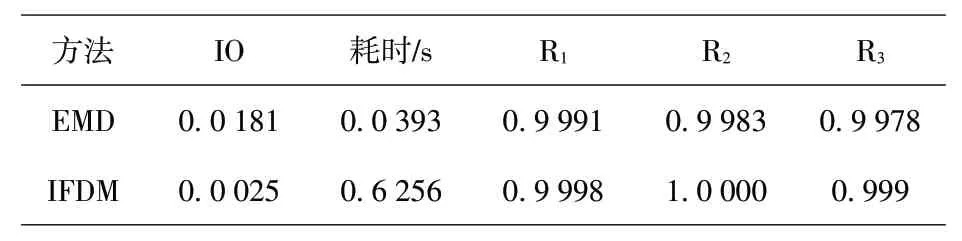
表2 y(t)评价指标对比
3 参数敏感性分析
由于1DRCAE 卷积核可以为一维振动信号发挥滤波器的效果,需要进一步探讨卷积核宽度引起的特征提取准确性与故障诊断性能的变化。图3给出了实验测试的结果。为对比误差相对下降幅度,图4 给出了相对长度的对比结果。可知,当卷积核达到较宽程度时,有助于更快提取出信号关键特征,而当卷积核太宽时则会引起大量冗余参数而干扰训练过程,无法实现网络特征的准确提取。
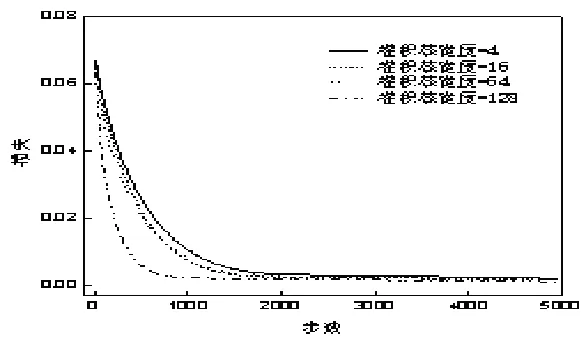
图3 采用不同卷积核的损失下降

图4 采用不同卷积核的故障识别准确率
4 结语
通过EMD 计算获得的3 个IMF 相对真实分量形成了较大的误差,采用IFDM 计算出的IMF 分量则跟真实分量之间形成了较小绝对误差,以IFDM方法处理时形成了比EMD更明显端点效应。
