面向小型四旋翼无人机的BPPID-LADRC串级抗扰控制器*

孙伟杰 万振刚

（江苏科技大学电子信息学院 镇江 212100）

1 引言

小型四旋翼无人机具有非线性、欠驱动、强耦合的特点，飞行控制系统是其研究的关键问题。目前国内外采用最多的仍然是传统串级PID 控制，其具有技术成熟、原理简单的优点，但是由于工程实际中小型四旋翼易受外界环境因素的干扰，且内外回路参数较多，不易整定，传统PID 控制很难满足稳定控制要求，因此，针对小型四旋翼无人机需要自抗扰能力更强、参数更易整定的控制器［1~4］。

自抗扰控制器（ADRC）具有控制精度高、响应速度快、抗干扰能力强等优势［5~8］，但是其参数过多且为非线性，难以整定。因此后来又诞生了一种线性自抗扰控制器（LADRC），其具有参数少的优势，便于参数调节和算法实现［9~10］。BPPID 控制器能够根据被控对象的误差变化自适应调整PID 参数，能够适应被控对象的非线性特性、时变特性以及内外部扰动，可以提高控制精度，同时通过神经网络的学习能力自适应地寻找合适的PID参数提升控制精度，相对于常规PID控制解决了参数整定难题［11~12］。

为此，本文针对小型四旋翼无人机的飞行控制问题，设计了一种BPPID-LADRC 抗扰控制器。该控制器中，外环位置回路的高度控制器和内环回路的姿态角控制器依据线性自抗扰控制理论（LADRC）设计，而外环位置回路的水平位置控制器则采用BP 神经网络PID 控制器。在强扰动条件下，分别对传统PID 控制器和BPPID-LADRC 抗扰控制器进行仿真对比实验，结果表明，BPPIDLADRC抗扰控制器更符合工程实际的需求。

2 BPPID-LADRC抗扰控制器设计

小型四旋翼动力学模型详见文献［13~15］，综合分析小型四旋翼的动力学模型可知，外环位置回路中高度方向的加速度不仅与小型四旋翼前后左右4 个旋翼的升力F1、F2、F3、F4有关，还与俯仰通道、滚转通道存在强耦合。同时俯仰通道、滚转通道、偏航通道之间也会相互耦合。此外，小型四旋翼在飞行过程中还会经常受到气流扰动、强阵风等外部扰动，这些不可预见的外部扰动通常会导致无人机姿态的波动和震荡，降低轨迹跟踪的精度。

传统PID 控制器在设计通道消除误差的同时，又会在其他耦合通道产生误差，相当于设计通道的控制作用在其他通道变成了干扰，这种控制量的耦合在小曲率快速机动时，对俯仰角、滚转角的影响尤为明显。

为此，本文设计了一种BPPID-LADRC 串级抗扰控制器，采用双闭环串级控制策略，原理框图如图1 所示。控制方式为高度z通道和偏航ψ通道采用自抗扰控制（LADRC）方法，横滚运动x-θ通道和俯仰运动y-φ通道采用外环BPPID+内环LADRC的串级控制。

图1 小型四旋翼无人机BPPID-LADRC控制原理框图

2.1 位置回路的控制器设计

高度z通道线性自抗扰控制（LADRC）由高度跟踪微分器TD、高度线性状态观测器（LESO）、高度线性状误差反馈控制律（LSEF）等部分组成。

1）高度跟踪微分器TD

高度跟踪微分器TD的作用为给定高度指令安排过渡过程，避免初始控制量过大造成的超调和震荡问题。高度跟踪微分器TD算法可以表述为二阶微分方程形式：

式（1）中，zd1是高度通道z经过高度跟踪微分器TD 柔化后的指令；zd为高度通道z的设定指令；r为调节过渡过程快慢的可调参数；h为滤波因子；fhan（·）函数为最速控制综合函数，其形式参见文献［10］。

2）模型线性化

令bo=cosθcosϕ，且Uz=U1bo-g，由小型四旋翼动力学模型可知则高度通道状态方程可表达为

由于小型四旋翼飞行机动时θ→0、ϕ→0 ，则可近似取cosθcosϕ=1 即bo=1，由此产生的误差折合到总扰动f中。

令x1=z,x2=ż，x3为高度通道总扰动f，y为系统输出，将动力学模型中高度通道的非线性系统近似为线性系统，具体如式（3）所示：

3）高度线性状态观测器LESO

对式（3）的新系统建立线性状态观测器LESO，则算法为

式中z1、z2、z3分别对应x1、x2、x3的估计值，β1、β2、β3是线性状态观测器LESO 中需要调节的参数，其数值由线性状态观测器带宽w0决定，由文献［9］和文献［15］推导可知，计算出β1=3w0,β2=,β3=。

4）设计线性状态误差反馈控制（LSEF）

针对前馈补偿后的积分串联标准型被控对象，可使用如下线性状态反馈控制律实现控制器的极点配置。其控制算法为

式（5）中：wc为线性误差反馈控制器带宽，其数值由极点配置法可以求得；Uz为待求控制量。求出Uz后，可求出U1。

水平位置x、y通道采用BP 神经网络PID 控制算法，控制器结构图如图2［11~12］所示，具体算法参考文献［11］和文献［12］，本文不再赘述。

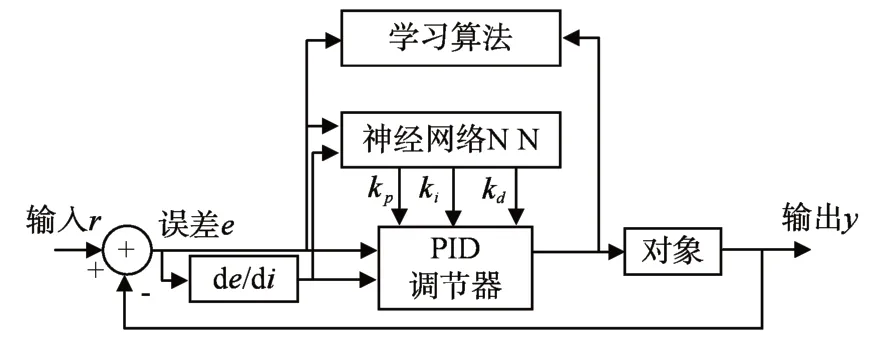
图2 BPPID控制器结构图

2.2 内环姿态回路的线性自抗扰控制器设计

由图1 和小型四旋翼动力学模型可知，小型四旋翼无人机的内环姿态回路是由俯仰角、滚转角和偏航角组成的3 个通道，其中俯仰角和滚转角通道通过位置通道外环BPPID 控制器经过几何运算解耦后计算得到，引入了虚拟控制量U2、U3、U4与其对应通道一一对应且相互独立。具体设计过程可参照上文高度通道LADRC控制器设计，不再赘述。

3 仿真实验与分析

根据上文，在Matlab软件环境中对小型四旋翼进行动力学建模，分别对传统PID 控制策略和BPPID-LADRC 抗扰控制策略在Matlab 软件环境下进行小型无人机飞行控制仿真。小型四旋翼的具体参数详见文献［10］。

BPPID-LADRC 抗扰控制器系统参数详见表1，其中初始权值是随机生成的，传统PID 串级控制器系统参数详见表2。

表1 BPPID-LADRC抗扰控制器具体参数

表2 串级PID控制器的控制器参数

分别在小型四旋翼的高度通道、俯仰角通道、滚转角通道以及偏航角通道加入强扰动ω1(t) 、ω2(t)、ω3(t)、ω4(t)。

具体表达式为

设小型四旋翼初始位置坐标为［0，0，0］，初始姿态角为［0°，0°，0°］，偏航角的设定值为60°。小型四旋翼的飞行期望轨迹为

对强扰动场景下小型四旋翼姿态的精准控制一直是难点，传统串级PID 控制器对内环3 个姿态角的控制效果如图3 所示，本文设计的BPPIDLADRC 控制器对内环3 个姿态角控制效果如图4所示。

图3 传统串级PID控制器对内环3个姿态角的控制效果

图4 BPPID-LADRC控制器对内环3个姿态角控制效果

由图3 和图4 对比明显可见，在4 个通道同时加入强扰动的情况下，PID 控制器无法实现对小型四旋翼姿态的有效控制，与期望姿态偏差明显，BPPID-LADRC 控制器只在阶跃干扰施加的瞬间有一定的跟踪误差，且跟踪误差能很快收敛到0，具有良好的跟踪精度。强扰动条件下串级PID 控制器轨迹跟踪效果如图5 所示，强扰动条件下BPPID-LADRC 串级控制器轨迹追踪效果如图6 所示。

图5 强扰动条件下串级PID控制器轨迹跟踪效果

图6 强扰动条件下BPPID-LADRC串级控制器轨迹追踪效果

由图5 和图6 对比可见：传统的PID 控制器在小曲率转弯部位出现了较大的轨迹跟踪误差，说明传统PID 控制无法满足小曲率轨迹跟踪的控制要求，而BPPID-LADRC 抗扰控制器轨迹追踪效果很好，能够满足小曲率轨迹跟踪控制要求。

通过图3、图4、图5 以及图6 的对比，充分说明了BPPID-LADRC 串级控制器具有出色的多通道解耦性能和抗扰动能力。

4 结语

本文针对小型四旋翼无人机飞行控制问题，设计了一种BPPID-LADRC 抗扰控制器。在四个通道同时加入扰动的情况下，对无人机的飞行位置和飞行姿态进行了控制仿真对比，经过参数整定，BPPID-LADRC 控制器均获得了良好的控制结果，对比传统PID 控制器，其控制精度更高，跟踪速度更快，具有更强的抗干扰能力，且控制器参数易整定。