基于星间可见性的振动监测可视化仿真研究

2023-09-28刘金磊曹炳尧李正璇

计算机测量与控制 2023年9期

刘金磊，曹炳尧，李正璇

(上海大学特种光纤与光接入网重点实验室，上海 200444)

0 引言

随着信息技术的高速发展，星间激光通信作为一种新型的通信技术，由于其具有低功耗、数据传输速率高、保密性强等特点，它对国家国防军事的战略意义以及民用生活的便利保障发挥着越来越重要的地位[1]。在卫星光通信过程中由于光束的发射角小，通信距离遥远，且空间环境复杂等问题，高精度且快速的捕获、跟踪、瞄准技术就显得至关重要[2]。卫星光通信对于ATP系统的性能要求较为苛刻，跟瞄精度需要达到微弧度量级，才能保持稳定的通信链路。在众多的环境干扰因素中，卫星平台振动是影响星间激光通信稳定性最重要的因素之一，无论是开环捕获还是闭环跟踪瞄准阶段，卫星平台振动都影响着通信链路的建立。

在空间光通信的研究中，ATP系统及其捕获、跟踪技术是研究的核心问题之一。在20世界80年代末期欧空局启动了SILEX计划[3]，在计划中ATP系统负责捕获、跟踪等功能，并采用高带宽精跟踪环，实现稳定跟踪；1994年日本邮电部通信研究实验室研制的卫星光通信基础实验系统LCE搭载在技术试验卫星ETS-VI发射升空，首次实现了地双向激光通信链路[4]，其ATP系统由粗跟踪、精跟踪和超前瞄准系统组成；2008年，德国宇航局实现了世界首次空间相干激光通信，采用无信标捕获的新技术，大大简化了ATP子系统的结构，捕获时间小于1 min[5]；2011年，哈工大自行研制的光通信终端与地面站建立了光通信链路[6]，上行传输速率20 Mbps，下行传输速率504 Mbps，平均捕获时间小于5 s，标志着我国在空间光通信领域进入在轨实验阶段。2012年，武汉大学艾勇团队研制了一种精跟踪系统，该系统的探测机构采用高帧频的CMOS相机，执行机构采用以音圈电机驱动的快速反射镜。分别对运动平台不同角速度转动、大气湍流、平台振动因素对跟踪精度的影响进行了模拟实验，该系统可实现6 μrad的跟踪精度[7]；自抗扰控制技术可以有效抑制诸如卫星平台扰动带来的影响[8-9]，文章[10]设计了滑模控制器组成的精跟踪控制系统，并对动态滞后跟踪性能进行仿真研究，滑模控制可增加系统的控制带宽，在较宽的范围内对粗跟踪系统产生的随机误差有较强的抑制能力。

鉴于国内外的相关研究来看，对于ATP系统的研究主要集中在捕获技术、精跟踪方案设以及振动抑制等方面，而在卫星平台振动对于链路影响的可视化技术方面研究较少，无法满足未来星网仿真的需求。

因此本文提出了星间激光链路状态模型，并搭建了针对卫星平台振动监测的可视化仿真平台。其中，星间激光链路状态模型包括了星间可见性模型、卫星平台振动模型、卫星姿态模型等与链路状态相关的参数，通过可视化手段完成对卫星平台振动的监测工作。星间可见性限制条件包括由可通过大气层厚度决定的星下地心角以及激光通信功率方程，在可见性的前提下，通过调整卫星姿态，并计算方位角、俯仰角保证建立激光链路的方向准确性，然后对通信链路叠加卫星平台振动，最后以可视化技术展示链路实时状态。

1 星间激光链路状态数学模型

卫星间建立通信链路会受到诸多因素影响，为了准确地仿真卫星真实的通信状态，需要建立链路状态数学模型来表征链路的通断状态，为此需要去研究和分析以下几个预算条件：为了防止地球遮挡激光信号，需要对卫星间的最大地心角进行研究；考虑到光信号在自由空间中的各种损耗，决定了可达的最大通信距离，需要对光功率链路方程进行研究；考虑到星间激光通信过程中，对方卫星的方向和距离是ATP系统需要考量的重要因素，需要对卫星的方位角、俯仰角以及星间距离关键信息进行计算分析；卫星平台振动是影响链路通信质量的关键因素，如果超过ATP跟踪精度则可能会使链路发生暂短中断，故需考虑平台振动对链路的干扰。链路状态的数学模型建立流程如下：

首先通过两颗卫星的空间坐标位置，分别计算卫星间的地心夹角以及激光功率可达范围从而确认两颗卫星间的可见性，如果可见则计算卫星间的方位角和俯仰角来确定激光发射方向进而建立通信链路，并叠加振动信号来干扰链路的稳定性，根据振动幅度与跟踪容限进行比较，来得出链路的通断状态。根据以上内容，本文提出的链路状态数学模型表达式如下所示：

LSsat1sat2=Gt·Pl·Vt

(1)

其中：LSsat1sat2表示卫星间的链路状态结果，为true或者false，含义为连接状态或断开状态。Gt代表地心角判断模型的输出结果，Pl代表激光功率模型的输出结果，Vt代表卫星平台振动模型的输出结果。

Gt、Pl、Vt的具体表达式如下所示：

(2)

式中，G代表卫星当前时刻形成的地心角，Gmax代表卫星可见时的最大地心角，Pr代表ATP探测器的接收功率，Ps代表探测器灵敏度，V代表当前时刻的振动幅度，Vmax代表ATP跟踪容限最大幅度。

1.1 地心角的预算条件

考虑到地球对星间链路的遮挡作用，影响星间链路通信。为了保证通信链路的正常，同一轨道高度的两颗卫星的位置应该满足以下关系公式：

式中，R为地球半径，h为卫星高度，a为卫星对应的地心角。

由于大气层对于星间链路的影响较大，所以为了避免通信链路受到低空复杂环境的干扰，保证一定的通信质量，一般规定不通过厚度为Hp的大气层，其取值不得小于几十公里[11]。故式(3)变换为：

(4)

在已知轨道高度的情况下，Hp将决定两颗卫星可以建立星间链路的最大地心角amax，其计算公式如下：

(5)

由于卫星任务的需要，建立星间链路的两颗卫星可能处于不同轨道高度。位于不同轨道高度的两颗卫星，在给定各自轨道高度和星间链路距离地面的最小值的情况下，可以确定两颗卫星建立通信链路的最大地心角amax：

(6)

式中，hA为卫星A的轨道高度，hB为卫星B的轨道高度，a为卫星A和卫星B形成的地心角，R为地球半径。

1.2 光功率的预算条件

在星间链路通信中，接收端接收到的光信号强度必须大于ATP探测器的最小探测值，才能实现可靠的光通信。在整个通信链路过程中，激光功率会发生衰减变弱，最后由ATP接收装置接收到的光功率方程可由式(7)表示。链路方程中包括了关键的参数和信息，对于星间链路的仿真具有重要意义[12-13]。

Pr=Pt·ηt·ηl·ηr

(7)

其中：Pr为探测器接收的效率，Pt为激光器发射的效率，ηt为激光发射系统的总体效率，ηl为激光在自由空间传输过程中的总体效率，ηr为激光探测系统的总体效率。

激光发射系统效率ηt主要由两方面影响，一方面与发射天线的增益Gt成正比，另一方面取决于发射光学发射系统的传输效率τt，它们的关系表达式为式(8)。其中，发射天线增益Gt与光束发射角θb(半角)成反比，当激光发射功率一定时，光束发射角越大，能量越分散，此时天线发射增益Gt就越小。

(8)

激光传输效率ηl与空间损耗Lr和大气透过率τα有关，其中大气透过率τα在星间通信时可将其设为1，其关系表达式为式(9)。在自由空间光通信过程中，随着空间距离越长将导致能量损耗增多，但波长越长的激光，其绕射和穿透能力比较强，信号损失衰减也越小，能够传输的距离越远。

(9)

激光接收系统总体效率ηr和三方面因素有关，分别是接收光学系统的传输效率τr、接收天线的增益Gr、跟瞄误差平均损耗τj，其关系表达式为式(10)。接收天线增益Gr又与接收天线孔径Dr和光波长λ有关，接收孔径越大，能够接收到的光束能量就越高，天线增益就越大[14]。

(10)

综上所述，合并公式(7)～(10)，星间链路建立的光功率方程为公式(11)所示：

(11)

式中，Dr、θb、σp、τt、τr均可视为常量，所以探测器接收到的光功率与通信距离关系密切。当激光的发射功率一定时，随着通信距离的增加，激光探测器接收到的功率越小。

1.3 方位角和俯仰角的计算

方位角和俯仰角决定了激光发射的方向，星间距离决定了激光功率是否可达，所以这三个指标在星间链路的可视化仿真中起着关键作用。

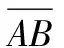
1.3.1 方位角和俯仰角的计算

(12)

(13)

(14)

(15)

(16)

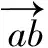
(17)

(18)

1)方位角的正负方向判断：

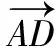
(19)

若σij≤90°，则ψij=ψij，方向为正；若σij>90°，则ψij=360°-ψij，方向为负。

2)俯仰角的正负方向判断如下：

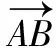
(20)

若ρij>90°，则φij=φij，方向为正；若ρij<90°，则φij=-φij，方向为负。

1.3.2 星间距离的计算

在时刻t，卫星i和卫星j的星间距离计算公式如下：

(21)

1.4 卫星姿态控制计算

卫星在轨运行时，往往需要与地面站或其他卫星进行链路通信，而卫星的位置与姿态处于不断变化中，如果不加以约束则很难建立起可靠的通信链路，本文针对这种情况，提供了一种在三维可编程建模平台中实现卫星姿态控制的方法，使卫星可以按照期望的姿态进行星间通信。

本文规定卫星无论何时都保持如下姿态：卫星Z轴指向地心位置，Y轴指向轨道面的法向量，X轴方向沿飞行方向，不一定与卫星的飞行速度矢量重合，而由Y轴与Z轴的叉乘方向决定。

在可视化三维编程平台中，可通过以下步骤完成卫星的姿态调整：

1)实现卫星定位。通过轨道预测模型计算得到卫星在当前时刻下地心惯性坐标系的坐标；然后经过与经纬高坐标系转换、三维编程平台内的空间直角坐标系转换以及局部坐标系转换；最终得到位于三维编程平台内的空间位置(x0，y0，z0)。

2)调整卫星的Z轴方向。通过式(12)得到轨道坐标系的Z轴向量，在三维编程平台内可以直接设置某个刚体的X、Y、Z轴向量，所以通过赋值操作完成卫星Z轴的调整，达到卫星朝向地球的视觉效果。

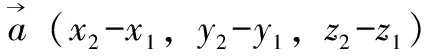
(22)

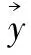
4)计算获得旋转方向。在已知旋转角度的情况下，需要得到当前卫星朝正向旋转还是朝反向旋转。判断方式与卫星的Z轴方向以及左右手定则有关。在本平台下，计算公式如下：

(23)

(24)

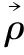
2 卫星平台振动模型

2.1 卫星平台振动特性

星上振源分为外部扰动源和内部扰动源。外部扰动源主要与卫星所处空间物理环境有关，包括太阳辐射压力、日月引力、微小陨石碰撞等；内部扰动源主要与卫星的自身机械操作有关，包括太阳帆板步进、天线机械运动、陀螺偏移等[16]。

国外许多航天机构为了获得准确的卫星平台振动数据，进行了很多振动实验，测得的卫星平台振动功率谱密度如图4所示。由LANDSAT-4卫星的振动功率谱可分析得到平台振动是由连续振动和谐波振动分量组成[17]。其谐波分量分别为：频率1 Hz，振幅为100 μrad；频率100 Hz，振幅为4 μrad；频率200 Hz，振幅0.6 μrad。欧空局通过对振动数据建模，其采用的振动模型功率谱密度函数为：

(25)

由此可以得知卫星平台振动具有一定的特点：低频率高幅度，高频率低幅度；卫星平台振动的振幅随着频率的增加而显著降低[18]。

2.2 卫星平台振动信号模拟

为了给卫星平台增加振动信号，需要根据欧空局的振动功率谱密度模型模拟出相似的振动信号。通过分析功率谱密度模型可知连续振动功率谱呈现低通滤波器的特点，谐波振动分量的功率谱密度呈现冲激信号特点，在时域上则表现为正弦信号。本文采用的谐波振动采用LANDSAT-4卫星上采集的三个谐波振动分量，可分别等效为：

x1(t)=100 sin(2πt)μrad

(26)

x2(t)=4 sin(2π×100×t)μrad

(27)

x3(t)=0.6 sin(2π×200×t)μrad

(28)

连续振动功率谱密度采用SILEX发布的卫星平台振动的功率谱密度函数，如式(25)所示。由于高斯白噪声是独立信号，表现为信号围绕平均值的一种随机波动过程，常用于信道噪声，所以本文采用高斯白噪声通过经设计的低通滤波器来模拟连续振动信号。经过设计测试，高斯白噪声的均方根值为2 μrad，低通滤波器的传递函数为[20]：

(29)

采样频率为5 kHz，滤波后的信号附加上正弦谐波信号，再经过功率谱密度(PSD，power spectral density)计算，为了突出低频区域特点，将结果转换为分贝，模拟得到的卫星平台振动信号的功率谱与卫星振动标准模型的对比如图5所示，由图可知，两者基本一致。

本文模拟的卫星平台振动分为连续振动信号和叠加了较短时间的谐波振动分量的振动合成信号，图6为连续振动信号的时域曲线，横坐标为时间、纵坐标为幅度。图7为合成信号的时域曲线，其中第4～6 s叠加了谐波振动分量。

2.3 平台振动对三轴自由度的影响

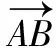
(30)

其中：A0表示振动信号的振幅，γx表示对X轴的振幅影响，γy表示对Y轴的振幅影响，γz表示对Z轴的振幅影响。

3 卫星系统振动监测平台的设计与实现

3.1 系统架构设计

卫星系统振动监测平台的系统架构设计如图8所示。整体系统框架分为三层，分别是数据层、机理层和表现层。数据层主要用于储存关键数据并为上层提供数据支持，数据引擎采用MySQL。物理空间的数据主要来源于TLE(two-line element)数据文件，包括轨道六根数、卫星预报的纪元时间、卫星号等；虚拟空间的数据来源于仿真系统的计算数据，包括卫星坐标、振动数据、图表数据、链路状态数据等。机理层是平台功能实现的核心层，完成了星间可见性计算和卫星平台振动模拟仿真两大功能，为振动监测提供了计算准确性和功能完整性保障。表现层是可视化展示部分，分为操作模块和可视化模块，其中操作模块包括了启动、暂停、重置、时间加速、振动叠加等功能，可视化模块包括了图表绘制、轨道显示、链路绘制、卫星数据实时刷新等内容。

3.2 振动方案设计实现

由于振动信号的仿真平台是Matlab，可视化三维编程平台为Unity3D，所以需要完成振动信号的导入方案设计以及振动信号的产生方案设计。

3.2.1 振动信号导入方案

振动信号的导入是将由Matlab产生的振动信号通过一定方式使其能够在Unity3D中复现，由此存在三种振动信号的导入方案。

第一种方案，由Matlab连续不断的产生离散振动数据，并与可视化仿真平台进行通信，通信方式可以为TCP或UDP。这种方式会导致仿真平台与Matlab的耦合性太强，降低了平台的扩展性，使用性受限，并且通信的实时性与触发时机也需要考虑，增加了整个系统的复杂性。

第二种方案，由Matlab生成一个具有一段时间的离散振动信号的数据文件，然后可视化仿真平台通过读取它获取振动信号。但这种方式的有效性是有时间限制的，如果平台运行时间超过了数据文件内规定的时间后，采用重复利用这个振动文件，则会给整个振动信号额外增加了一个周期性的因素，从而出现问题。并且振动文件的时间如果过长，文件占用内存就越大，生成速度就越慢，访问速度也会受到限制。

第三种方案，在可视化仿真平台内部产生振动信号，并且控制固定周期下产生一次振动信号，保证整个运行周期下模拟振动信号的功率谱密度是符合卫星平台振动模型的。由Matlab将产生固定周期的振动信号的代码封装成函数；将此m文件经过编译后转换为dll动态链接库；在Unity3D的环境下引用此动态链接库，实现固定周期的振动信号的生成，并且不同固定周期下的振动信号也是具有随机性。

经综合评估后，第三种方案更加符合系统要求，在理论性和实时性上都具有较好的表现，本文最终选择第三种方案作为振动信号的导入方案。

3.2.2 振动信号产生方案

振动信号的导入方案规定采样频率为5 kHz，输出时间间隔为1 s的振动离散信号。经过测试，由Matlab生成振动信号消耗的时间为3 ms，由Unity调用dll动态链接库生成振动信号消耗的时间为70 ms，两者生成振动信号的速度都相对较快。由于振动信号每秒输出5 000个离散点，Unity画面显示的平均帧率为320 fps，所以需要建立每帧显示的振动幅度与离散点的映射关系，其映射公式如下所示：

i=N*(φ-INT(φ))

(31)

其中：N是离散点个数，φ是Unity中当前帧的时间时刻，单位是秒，包含了毫秒部分，INT()是取整函数，用于对浮点数向下取整，i是计算后得到的离散点下标索引。

振动信号需要在使用的当前秒之前生成，否则会造成生成振动信号的这段时间的显示空白。为了解决这个问题，本文采用了队列缓存技术的方式解决。

队列具有先进先出的特点，且可以规定队列允许的元素数目，很适合此场景下使用。具体步骤如下：

1)在平台控制界面点击启动按钮前，提前生成1s的振动离散信号数组，并入队到缓存队列中。

2)当点击启动按钮时，从缓存队列中获取位于队列首部的振动信号数据，并根据公式(31)计算每帧输出的振动幅度，并判断振动幅度与规定的ATP跟踪容限幅度的关系，进而显示卫星之间的连接状态。

3)开启子线程，在子线程中生成下一秒的振动信号数组，并入队到缓存队列中，此时缓存队列中存在当前秒及下一秒的振动离散数据。

4)下一秒时，会产生新的振动信号，由于上一秒的振动信号已经失去作用，所以规定缓存队列的元素数量为2，队列首部的振动信号数组被出队，新的振动信号数组入队。

4 实验结果与分析

本实验分别对星间可见性计算的准确性和卫星平台振动监测功能的有效性进行验证：在星间可见性计算准确性方面，一组数据为本实验平台输出的方位数据，另外一组为STK的仿真数据作为对照，将两组数据进行误差对比，并对关键时间点进行分析；在卫星平台监测有效性验证方面，选择两颗同轨卫星，在建立通信链路之后使卫星平台产生突发振动信号，将链路断连状态与产生的振动信号进行对比，以验证有效性。

本实验从CelesTrak官网获取Starlink卫星在2022年12月4日的TLE数据，异轨卫星组为STARLINK-1042和STARLINK-1228，用于星间可见性计算的准确性验证。

4.1 实验平台

本文采用Unity3D作为三维可视化编程平台，使用TLE文件作为输入，星间链路状态作为输出，实时渲染卫星通信链路状态及轨道运行情况。本次实验服务器使用的操作系统为Windows 10，为了提高画面流畅度和计算性能，本平台采用了32 GB大内存、高性能CPU和GPU。

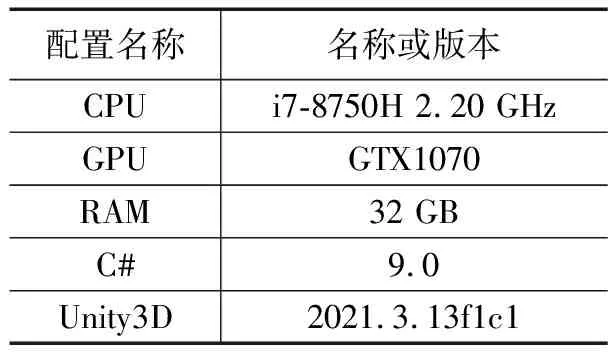
表1 服务器配置信息

4.2 星间可见性的实验验证

本实验的仿真时间为格林威尼时间2022年12月4日8：33到2022年12月4日9：35(本实验中的卫星环绕地球一圈的大致时间)，时间步长为30 s(共62个采样点)。由于STK对于可见性的判断仅有地球遮挡为条件，所以本仿真平台也将可见性条件调整为仅地球遮挡。在统一可见性条件下，在STK软件上创建STARLINK-1228指向STARLINK-1042的链接，并在仿真时间范围内输出方位角、俯仰角和星间距离，与本文的可视化仿真平台输出结果进行对比，实验结果如图9所示。

从图9(a)～(c)可知，平台的实验数据与STK的仿真结果趋势接近，从图9(d)可知方位角的计算误差在30之内，俯仰角的计算误差基本在10以内，星间距离的计算误差大致在110 m以内，其计算准确性可以支持卫星相关仿真实验的正常使用。

从图9可知，STARLINK-1228与STARLINK-1042在仿真时间内，从第一次链路通信到链路断开的时间为08：47，第二次建立通信链路的时间为09：18。08：47～09：18这段时间两颗卫星处于不可见状态，所以无法进行链路通信，也不会输出相应的方位角、俯仰角和星间距离，验证了本文星间可见性方案的准确性。

本文提出星间可见性条件中包括由大气厚度计算得出的地心角判断以及激光功率可达距离判断，在仿真时间范围内，在本可视化仿真平台的可见性判断中增加这两个条件，其预算参数见表2所示，将本可视化仿真平台的实验数据与STK的可见性时间进行比较分析，实验结果如下所示：

由于根据大气厚度计算最大地心角对应的星间距离超过4 000 km，与激光最远可达距离比较，两者取最小值，以4 000 km为临界值。由图10可知，在本仿真平台下卫星的链路通信时间比STK的通信时间短，且在星间距离达到4 000 km附近时，本仿真平台的卫星链路发生断开，与此同时STK的卫星链路会继续通信一段时间后才断开，其实验结果验证了本平台星间可见性限制条件的有效性。

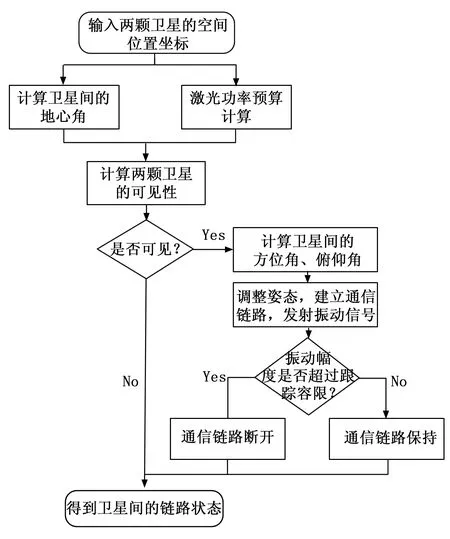
图1 星间链路状态数学模型建立流程

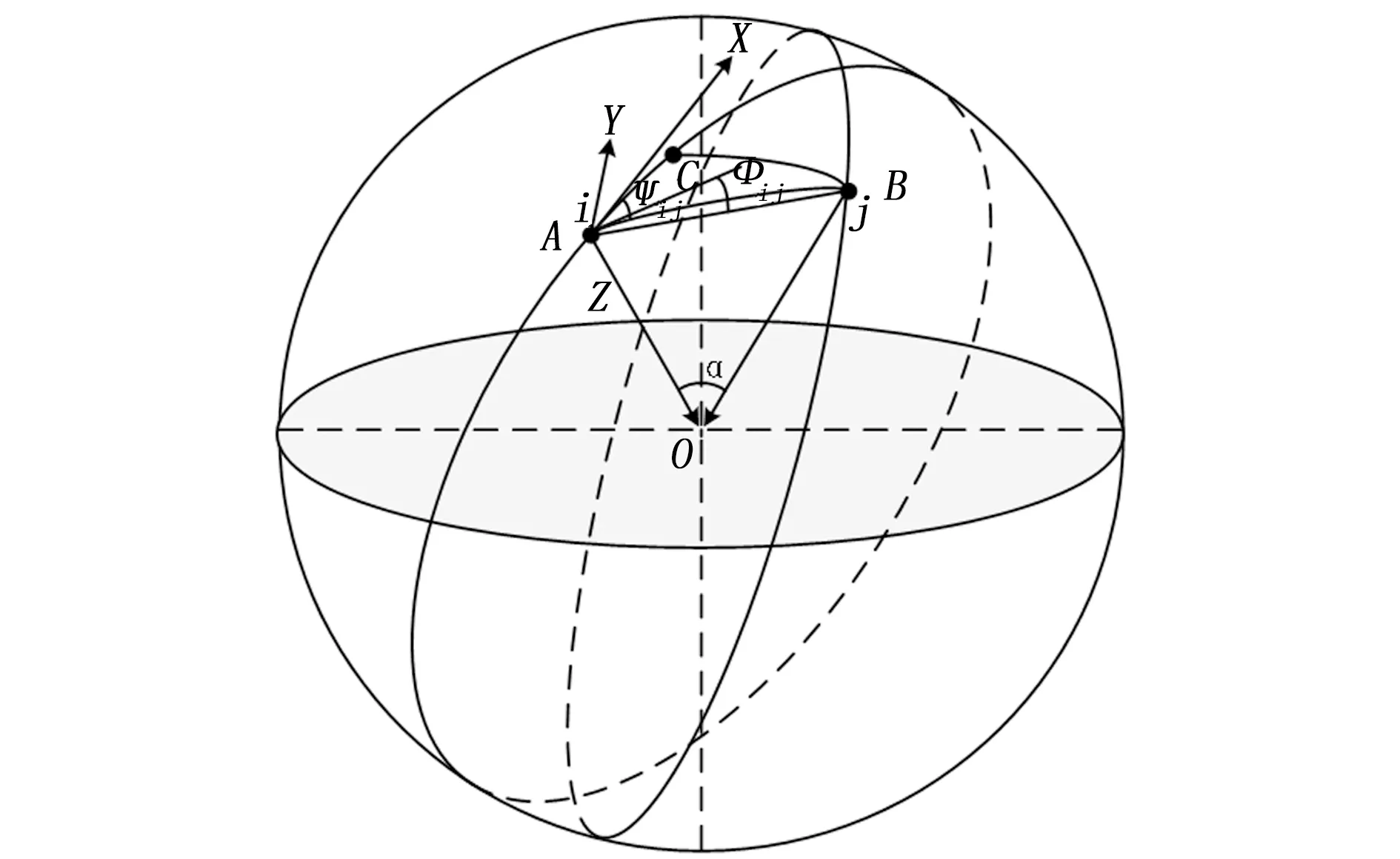
图2 不同轨道平面下两颗卫星的几何关系

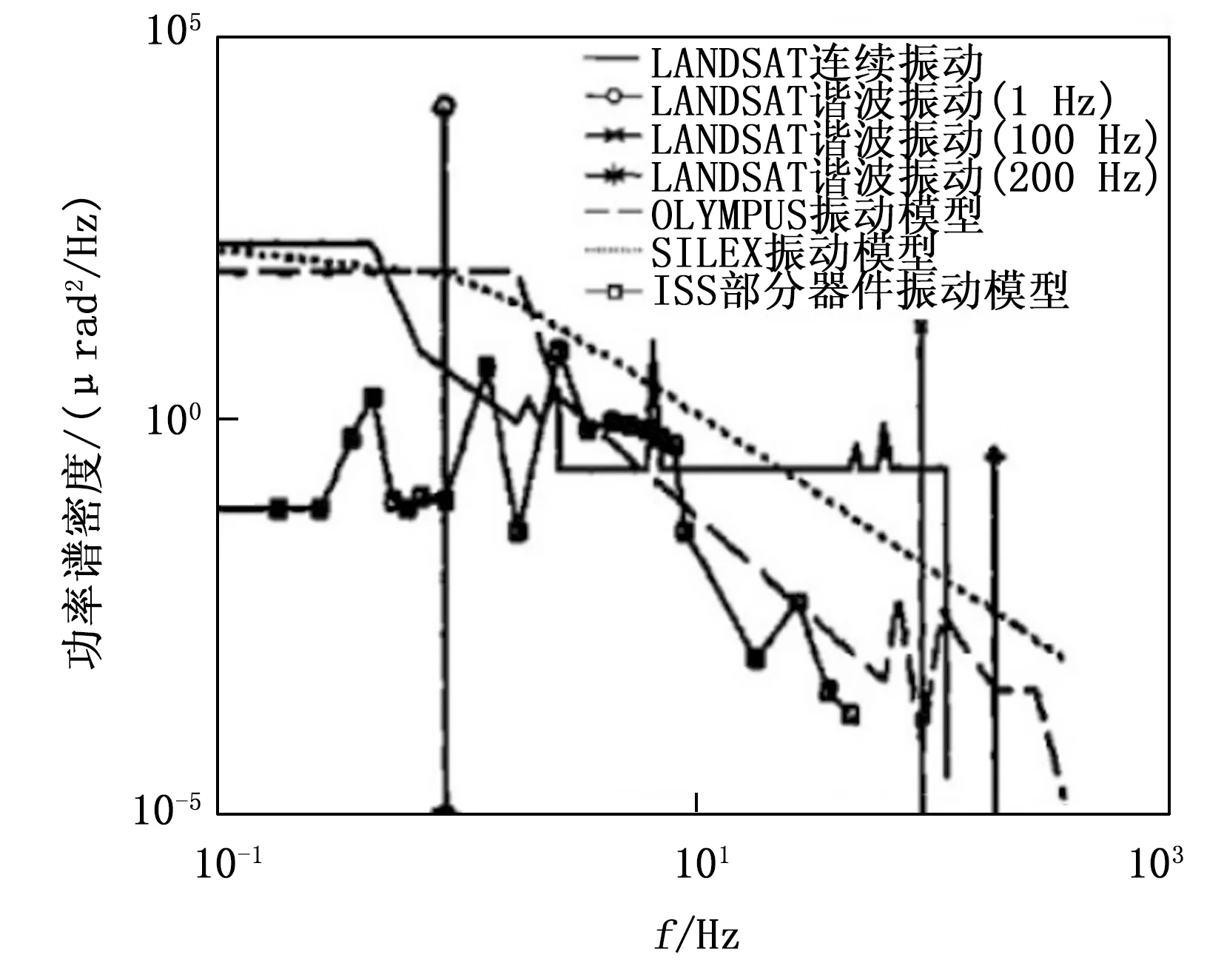
图4 各种典型平台振动功率谱密度图[19]

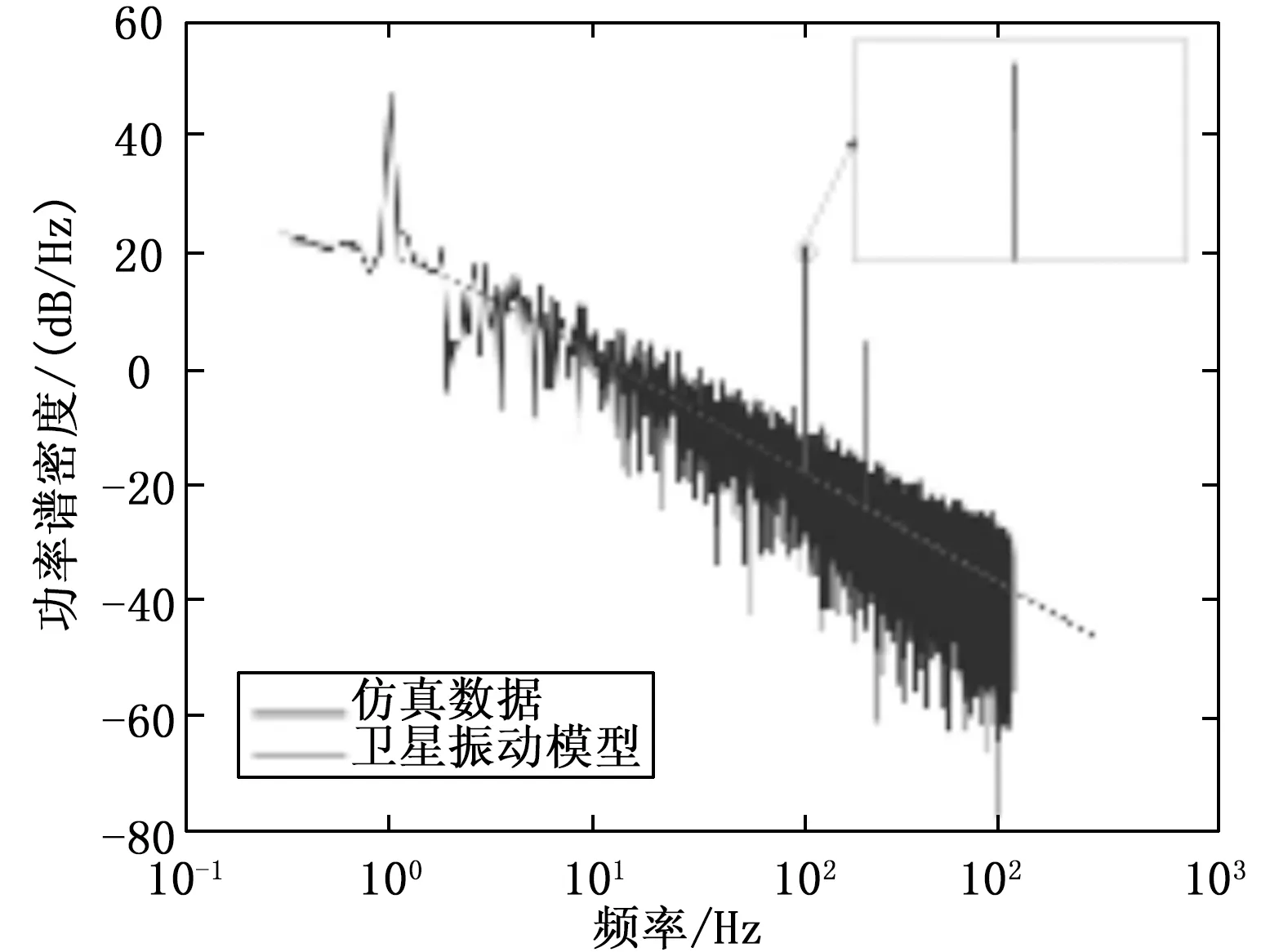
图5 模拟振动信号与卫星振动模型PSD对比图

图6 卫星平台连续振动信号的时域图

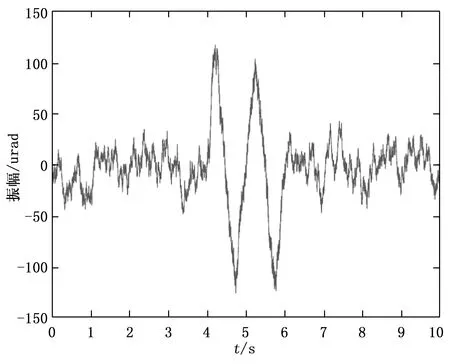
图7 卫星平台合成振动信号时域图

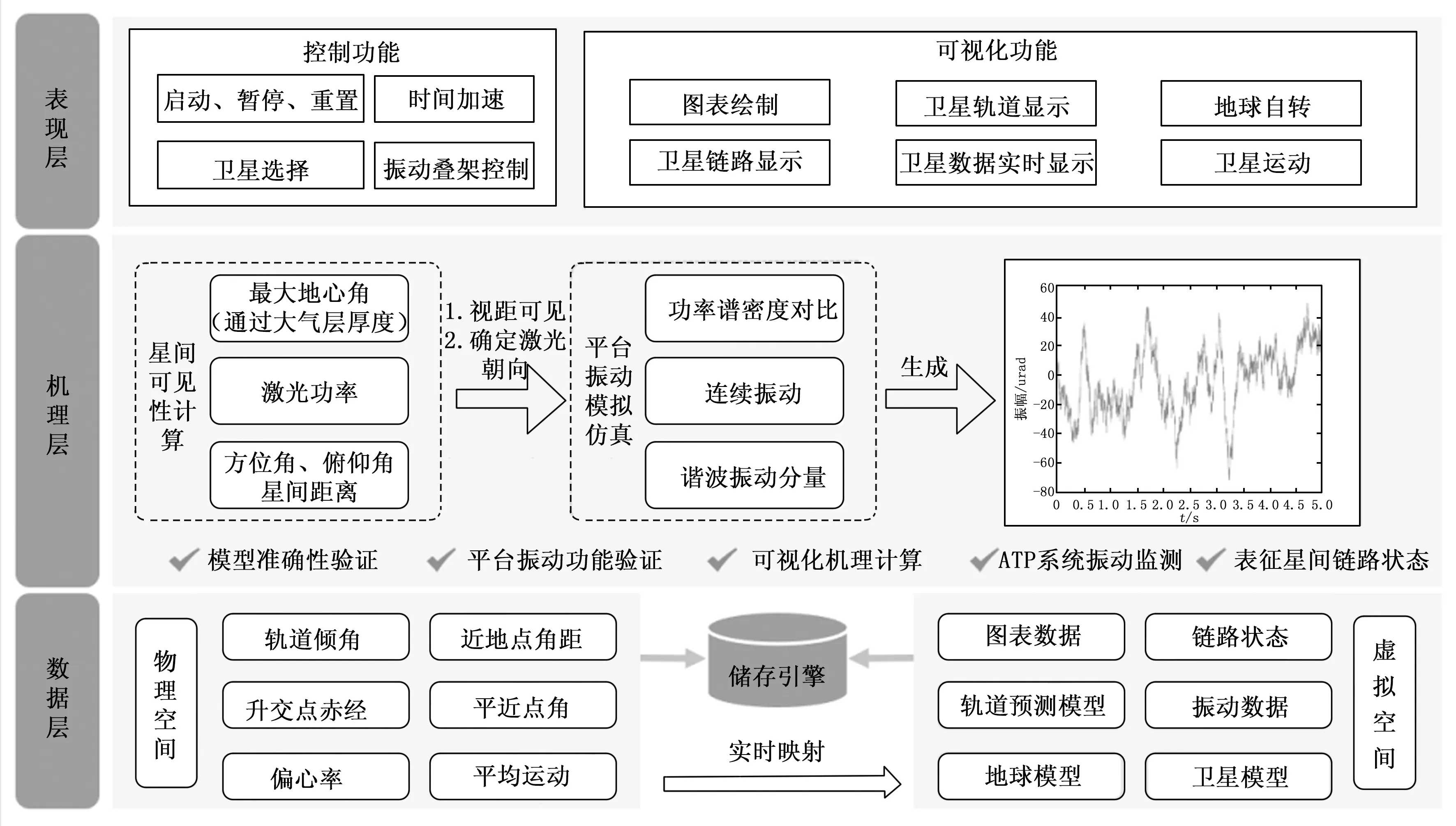
图8 系统架构图

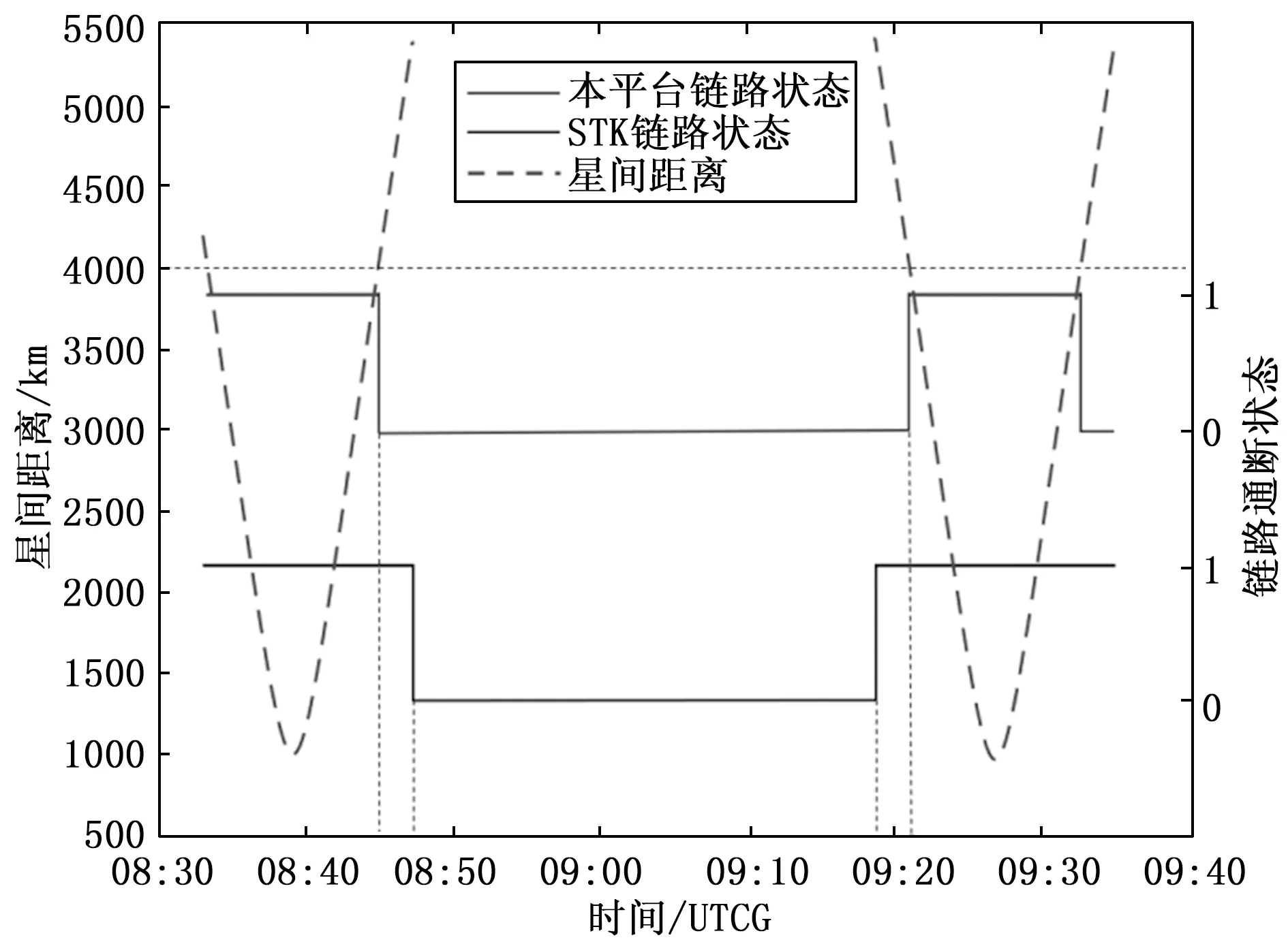
图10 本仿真平台与STK可见性条件功能验证

4.3 振动监测的有效性验证

本实验的仿真时间为格林威尼时间2022年12月4日08：40：00～08：40：10，在星间链路连通的情况下，叠加连续振动信号，并在08：40：04～08：40：06时间段添加了谐波振动分量。本仿真平台设置ATP的跟踪精度为80，在仿真时间内，星间链路断连状态如图11所示。

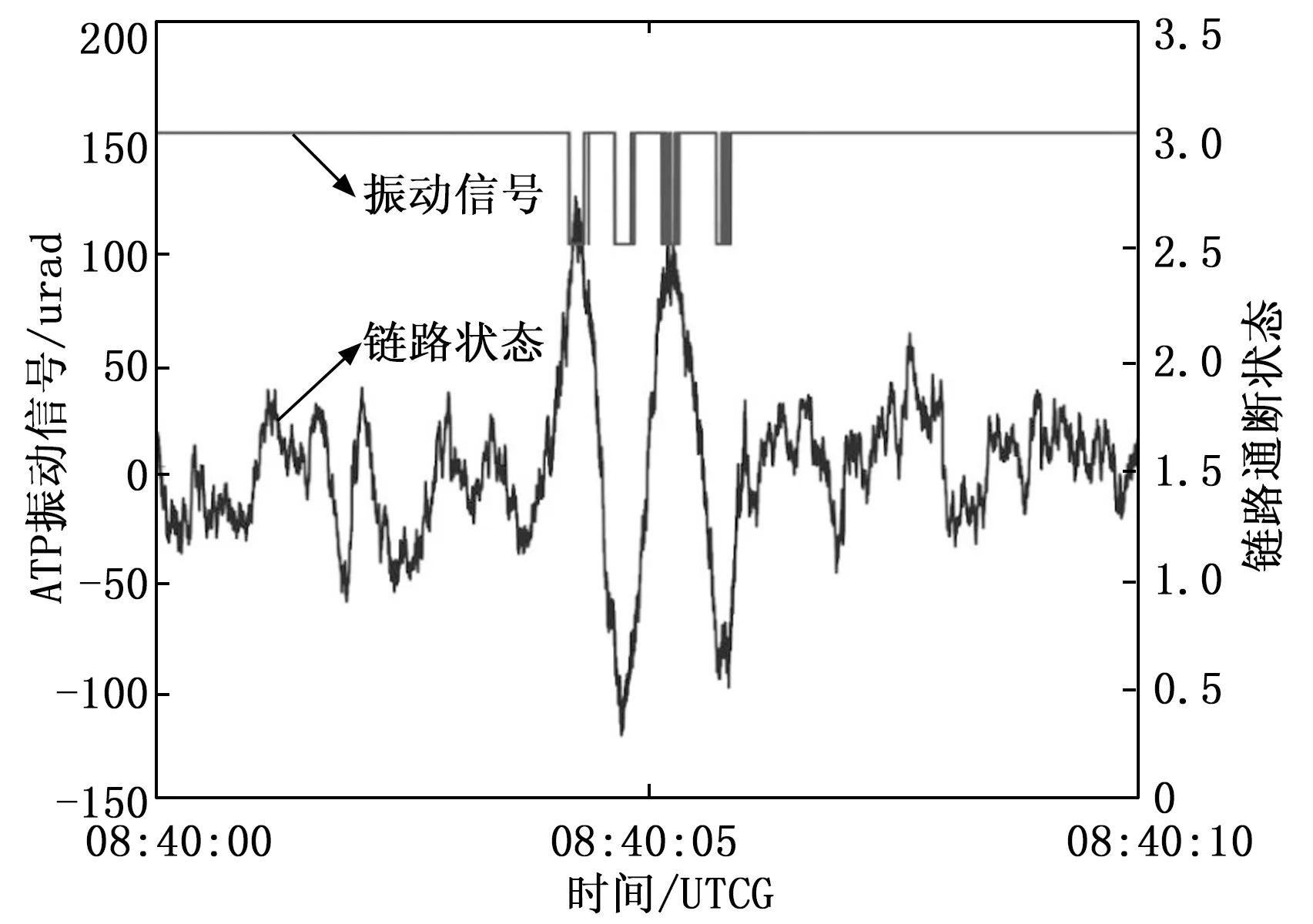
图11 平台振动对星间链路的干扰关系图

从图中可以看出，在连续振动阶段，振动信号的振幅始终小于80的阈值，星间链路一直处于连接通信状态；在时间段08：40：04～08：40：06，谐波振动分量使振动幅度变大，超过阈值的时间段表现为链路断开；从08：40：07开始，谐波振动消失，星间链路保持正常通信。实验结果验证了本平台对振动监测的功能性良好，可以较好捕捉卫星平台振动幅度超过阈值的时间段。