基于改进粒子群算法的单产品多厂协同生产决策方法*

张跃伟, 胡 敏, 高孝天

[1.上海电器科学研究所(集团)有限公司, 上海 200063;2.上海电器科学研究院, 上海 200063]

0 引 言

随着现代社会市场竞争的日趋激烈,市场条件的不断变化使得供应链上的原材料供应、产品设计研发、生产制造、销售、流通等各个环节的信息交流更加密切。供应链内产品在生产运行时往往具有自洽性、分布性、异构性以及并行性等特点,这些特点都会向供应链管理提出新的挑战[1]。

制造企业的全球化发展既为企业带来了发展机遇,同时也面临着巨大的挑战。企业为了提高产品生产质量、降低生产成本、增强产品市场竞争力,不得不寻求新的生产管理模型来应对这些关键因素。于是现在绝大部分制造企业将有限的资源放在核心业务上,将非核心业务外包给行业相关企业,并与之成立行业产业链联盟。联盟的成立,使得各方能够充分利用资源,达到快速响应市场需求的目的。制造企业可以根据客户的订单要求,在行业产业链联盟内完成原材料的采购、产品分销、储存及运输等流程,极大地提高了制造企业的生产效率,同时也带动了行业产业链联盟内其他企业的发展,完成了初步的产业链协同。

在分布式制造企业中,产品的制造和设计阶段往往是通过不同地域的企业共同协助完成的,产业链协同生产使得产业链联盟中不同企业核心资源的利用发挥到了极致[2]。在产业链协同的运行流程中,产品分配问题涉及到能否按时按质地完成对用户的交付工作,所以在整个产业链内,产品分配问题最为关键。针对这一问题,文献[3]采用多智能体技术,构造协同生产系统框架,并提出模型层、加工层和系统层之间的协同生产运作模型。文献[4]采用模拟退火算法,文中主要考虑交易成本、采购成本、不良产品以及信誉评价等内容,建立了多目标整数规划订单分配模型。文献[5]中采用混合遗传算法,建立了面向供应链的多产品、多时段的订单任务分配方法,为后续相关问题的研究提供了思路。文献[6]采用分配启发式算法,并考虑实际生产和运输能力,建立以最小化供应链单位时间平均费用为目标的生产订单分配模型,文中对于订单分配决策问题进行了详细的分析和建模,具有较高的参考价值。

本文在上述研究的基础上进行拓展,从供应链的角度着手,并考虑每个车间的实际生产和运输能力,抽象出一个单产品多厂协同生产决策问题,并以完成用户需求总费用最小为目标,对各个厂区的产品进行优化分配。本文采用改进粒子群算法对该问题进行求解,并引入模拟退火操作,可以在每次求解中以一定的概率允许移动到比当前解稍差的点,从而使得算法的搜索性更强,保证了算法能够跳出局部最优。最终通过Matlab验证了所提算法的有效性,并且与遗传算法对比,所提算法收敛性更佳,具有更好寻优效果。

1 单产品多厂协同生产决策问题

1.1 问题的提出和前提假设

一条相对完整的产业链中应至少包括供应商、制造企业以及客户3种角色,其中供应商、制造企业以及客户都包含多个部分。制造企业根据客户提供的产品需求订单,在每个生产周期统一向供应商采购原材料,制造企业应能根据每个生产车间的生产能力,决策各个生产车间的产品订单分配以及产品的生产周期,使得单位时间的平均费用最少[7]。供应链流程图如图1所示。

图1 供应链流程图

该问题中同时还应满足如下前提假设:① 每个生产周期,制造企业统一向供应商采购原材料,其中不考虑原材料采购不足的影响;② 制造企业各个生产车间均能生产订单产品,但是各个车间的生产能力和效率可能存在差别;③ 产品生产和运输过程中不考虑损耗问题。

1.2 决策问题的数学模型

单位时间平均费用包括:① 原材料采购费用。② 产品生产和订购费用。③ 库存管理费用。第一部分主要是原材料的采购费用;第二部分主要包括生产装设费、产品运输费以及产品订购费;第三部分主要包括原材料、产品、仓库2以及用户处的库存管理费。单位时间平均费用可表示为

minF=F1+F2+F3

(1)

第一部分费用可表示为

F1=Ar/T

(2)

式中:Ar——产品的原材料订购费用;

T——产品生产周期。

第二部分费用可表示为

F2=(Sp+X(Aw+Ac))/T

(3)

式中:Sp——产品的生产准备费用;

X——单位生产周期内产品从仓库2运输到用户的频次;

Aw——产品从仓库2到用户的运输费用;

Ac——用户订购产品的订货费用。

第三部分费用可表示为

(4)

式中:Hr——原材料在仓库1的年库存管理费;

hj——单位产品在生产车间j的年库存管理费;

Hw——产品在仓库2的年库存管理费;

Hc——产品在用户的年库存管理费;

Ir、Ij、Iw、Ic——原材料仓库、在制品仓库、仓库2以及用户仓库的平均库存。

假设生产车间产品分配率为Yj,则该生产车间的生产时间为YjDT/Pj,运输时间为YjDT/dj,则在制品仓库平均库存计算如下:

(5)

式中:Yj——产品在生产车间j的分配率;

D——产品的年需求量;

dj——产品从生产车间j运输到仓库2的年运货量;

Pj——生产车间j的年生产能力。

同理,其他仓库库存计算如下:

(6)

(7)

(8)

将以上各仓库库存代入式(2)～式(4)中,可得出下式:

(9)

综上所述,单位时间平均费用可重写如下:

(10)

在进行产品分配时还应考虑到生产车间的生产能力和运输能力问题,原则上每个生产车间的产品分配不宜超过其生产能力和运输能力,则会产生如下约束条件:

(11)

2 改进粒子群优化算法(IPSO)

粒子群算法作为群体优化算法之一,由于其收敛速度快、参数少、算法易于实现等特点,被广泛用于路径规划、函数寻优、参数辨识等多个领域。但是该算法也存在可能会陷入局部最优的问题,为了解决该问题,文中采用模拟退火的思路,允许在求解过程中以一定的概率移动到比当前解稍差的解,从而增强算法的搜索区域,避免陷入局部最优解。

模拟退火算法步骤可分为如下4个步骤:

(1) 通过映射函数得到一个由当前解映射到解空间的新解,映射函数如下所示:

T_fit(x)=e-(fm(x)-fym)/T

(12)

式中:fm(x)——第x个粒子的最佳适应度;

fym——群体最佳适应度;

T——初始温度。

(2) 计算与新解所对应的目标函数增量比值。

(3) 采用轮盘赌策略(Metropolis准则)判断新解是否被接受。

(4) 如果新解被接受,则用新解代替当前解,进行下一次迭代过程。

与粒子群算法相比,模拟退火算法收敛速度较慢,但其具备渐进收敛性,最终能够实现全局最优解。粒子群算法与模拟退火的结合使得算法具备运算速度快、收敛特性好的特点,提高了标准粒子群算法的局部寻优能力。

学习因子c1、c2决定了个体粒子经验信息和种群最优粒子经验信息对粒子寻优轨迹的影响,反映了粒子之间的信息交换。在算法寻优初期,应该采用较大的c1值和较小的c2值,使粒子尽量铺满整个寻优空间,增加空间内个体粒子的多样性;而在寻优后期,则应该采用较小的c1值和较大的c2值,加强粒子向全局最优点的收敛能力。为实现学习因子的动态调整,本文采取一种椭圆型函数来自动调节学习因子。椭圆型函数如图2所示。

图2 椭圆型函数

由于决策问题本身存在等式约束条件,需要在算法中的目标函数部分加入处理措施。本文采用惩罚函数作为目标函数附加项,以实现算法的等式约束。

objF=F+η[1-sum(y1,y2,y3)]

(13)

式中:η——惩罚系数,该值应为一个较大值,文中取106;

y1、y2、y3——代表3个不同生产车间的分配率。

3 算法实例

本节采用两种不同的设计算例来验证算法的性能,并与标准粒子群算法和遗传算法的结果对比,验证所提算法的有效性。假设在某制造企业中,3个位于不同地域的生产车间均可生产用户需求产品,产品生产过程基本参数如表1所示。

表1 产品生产过程基本参数

算例一,假设车间生产能力高于产品运输能力,算例一的相关参数如表2所示。

表2 算例一的相关参数

算例二,假设存在生产能力不满足产品运输能力,算例二的相关参数如表3所示。

表3 算例二的相关参数

算法采用MATLAB语言编程实现,算法选取种群数量为50,迭代次数为500,遗传算法使用参数与之相同。惯性权重取值区间为[0.95,0.4],速度因子c1取值区间为[2.5,1.25],速度因子c2取值区间为[1.25,2.5]。算例结果对比如表4所示。

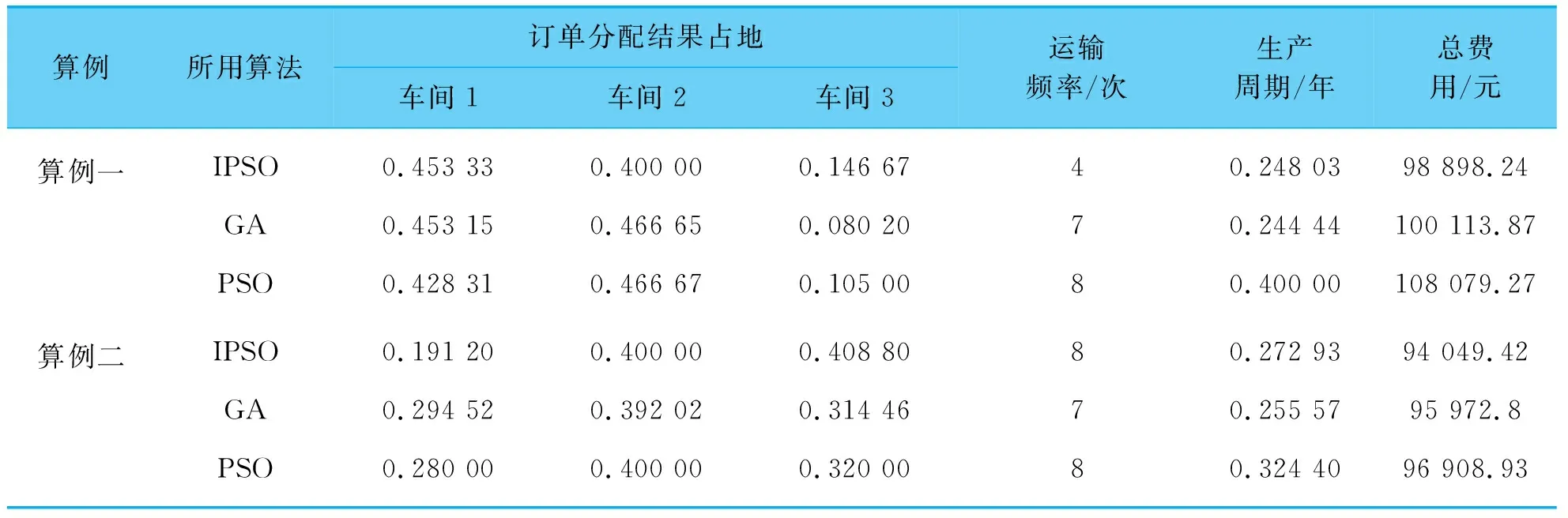
表4 算例结果对比

从表4的两个算例中可以得出结论,当车间生产能力高于运输能力时,产品订单的分配更多会倾向于运输能力强的车间;而车间生产能力低于运输能力时,产品订单的分配主要关注车间的生产能力。算例一目标值过程曲线如图3所示。由图3中可知,文中所提算法的空间搜索能力相比于标准粒子群算法和遗传算法有了较大的性能提升,并且收敛速度更快,避免了陷入局部最优解的情况。在相同参数条件下,能够实现更佳的寻优效果,体现了所提算法的有效性。

图3 算例一目标值过程曲线

4 结 语

本文研究了生产制造领域中的订单任务分配问题,提出了一种基于改进粒子群算法的单产品多厂协同生产决策方法,并考虑到实际生产情况中运输条件和生产能力等限制因素。粒子群算法和模拟退火算法相结合,使得算法兼顾收敛能力和寻优速度,性能有了较大的提升。文中目前只考虑到了单产品分配问题,后续还会继续研究多产品多厂的协同生产决策,进一步优化生产目标函数,使得该问题的解决方案更加完善。