Generalised tanh-shaped hyperbolic potential: Klein-Gordon equation’s bound state solution

V H Badalovand S V Badalov

1 Institute for Physical Problems,Baku State University,1148 Baku,Azerbaijan

2 Theoretical Materials Physics,Paderborn University,D-33098 Paderborn,Germany

3 Theoretical Physics VII,University of Bayreuth,D-95440 Bayreuth,Germany

Abstract

The development of potential theory heightens the understanding of fundamental interactions in quantum systems.In this paper,the bound state solution of the modified radial Klein-Gordon equation is presented for generalised tanh-shaped hyperbolic potential from the Nikiforov-Uvarov method.The resulting energy eigenvalues and corresponding radial wave functions are expressed in terms of the Jacobi polynomials for arbitrary l states.It is also demonstrated that energy eigenvalues strongly correlate with potential parameters for quantum states.Considering particular cases,the generalised tanh-shaped hyperbolic potential and its derived energy eigenvalues exhibit good agreement with the reported findings.Furthermore,the rovibrational energies are calculated for three representative diatomic molecules,namely H2,HCl and O2.The lowest excitation energies are in perfect agreement with experimental results.Overall,the potential model is displayed to be a viable candidate for concurrently prescribing numerous quantum systems.

Supplementary material for this article is available online

Keywords: Klein-Gordon equation,hyperbolic potential,Nikiforov-Uvarov method,diatomic molecules

1.Introduction

Following quantum mechanics’ genesis,the study of precisely solvable problems plays a critical role in comprehending the underlying quantum-mechanical systems [1-3].Analytical solutions of the Schrödinger,Klein-Gordon(KG),and Dirac equations are of particular importance in quantum mechanics because the wave function contains all the information necessary for a complete description of a particle’s behaviour in a force field [3-8].

In any n radial and l orbital quantum states,a limited number of physical potentials can be solved exactly for the Schrödinger,KG,and Dirac equations[2,3].Generally,many quantum systems can only be solved numerically or through approximation techniques [7-9].Therefore,several methods including the supersymmetry method [10],the factorisation method [3],the Laplace transform approach [11],the path integral method [12],the Nikiforov-Uvarov (NU) method[13],asymptotic iteration method [14,15] and the quantisation rule method [16-18] have been developed so far and they have been applied for the solution of the quantum wave equation.The NU method yields more practicality to solve second-order differential equations by transforming them into hypergeometric-type equations.Furthermore,the various exponential and hyperbolic potentials are analytically solved by using different approximation schemes with the NU method.

In principle,the exponential potential models always draw considerable attention and are widely used in various physical systems,including quantum cosmology,nuclear physics,molecular physics,elementary particle physics,and condensed matter physics [19-29].Up to now,many exponential-type potentials,including the Morse[30,31],Hulthén[32-38],Woods-Saxon [27,39-43],Rosen-Morse [44-48],Eckart-type [49-51],Manning-Rosen [52-54],Deng-Fan[55,56],Pöschl-Teller like [57],Mathieu [58],sine-type hyperbolic [59] and Schiöberg [60-63] potentials have been investigated,and some analytical bound state solutions were obtained using an approximation for these models in l ≠0 state.Some known exponential potentials can also be transformed into a hyperbolic potential model,which can help understand quantum systems’ natural dynamics [64-76].For instance,the thermodynamic properties of some molecules have been successfully predicted using the improved Rosen-Morse potential and the Fu-Wang-Jia potential to describe the internal vibrations of molecules [77-82].

Motivated by the simplicity and applicability of the generalisations of the hyperbolic potentials,the generalised tanh-shaped hyperbolic potential (GTHP) [83] was recently proposed as follows:

where V1,V2,V3are the depths of potential well and α is the adjustable parameter representing the properties of the interaction potential.For clarity about potential,see also the S2 section4.GTHP is the general case of the significant physical potential such as the standard and generalised Woods-Saxon[39,42],Rosen-Morse [44],Manning-Rosen type,generalised and standard Morse[30],Schiöberg[60],four-parametric exponential-type [67-69],Williams-Poulios potential[84,85],and the sum of the linear and harmonic oscillator potentials,see S2 section in4See supplementary material,which includes[29,56,and 63],for additional details of potential information and theoretical derivations..As it seems,GTHP’s characteristics can be used to explain the interactions of molecular,atomic,and nuclear particles.

In this study,we extend our study of GTHP by considering it in the KG equation.We apply the NU method to analytically solve KG and obtain the bound state for this potential,and we compare the results with the previously reported ones in particular cases.Then,the potential is modelled for several diatomic molecules,and the obtained results are in good agreement with experimental ones.This study allows us to correctly explain a broad variety of quantum systems’ characteristics and behaviour,including retardation effects,without needing a great deal of complex derivation or massive computing resources.The remainder of this study covers the following sections: the bound-state solution of the radial KG equation is presented in section 2.In section 3,we explore the results for energy levels and the corresponding normalised eigenfunctions in some special cases and diatomic molecules.Finally,some concluding remarks are stated in section 4.

2.Bound state solutions

The time-independent KG equation with scalar and vector potentials S(r)and V(r)a spin-zero particles takes the general form: [2]

where E is the relativistic energy system an M denotes the rest mass of the particle.To denote the radial and angular components of the wave function ψnlm(r,θ,φ),the concept of variable separation is defined as:

and substituting it into equation (2),the modified radial KG equation is obtained as follows:

After choosing of equal scalar and vector potentials,that is,S(r)=V(r),equation (4) becomes in the following form:

Considering the expression of 2V(r) equal as equation (1),that is

It should be noted that this choice the potential enables us to reduce the resulting relativistic states to their non-relativistic limit under appropriate transformations.Therefore,we obtain it as:

This equation cannot be solved analytically for l ≠0 due to the centrifugal term.Therefore,the Pekeris approximation[40-42,83,86]which is the most widely used and convenient for our purposes can be taken to solve this equation.According to the Pekeris approximation scheme to deal with the centrifugal term is used [83]

where the parameters A0,A1and A2were found as: [83]

After inserting the equation (8) into equation (7),and further using a new variabletanh(αr)=s,s ∊[0,1],we obtain it as:

where

with the boundary conditions χ(0)=0 and χ(1)=0.Now for implementing the NU method,equation (10) should be rewritten as the hypergeometric type equation form as:

After comparing equation (10) and equation (12),we obtain:

The new function π(s) as given in [13] can be obtained by substituting equation(13)and takingσ′ (s)=-2s.Hence,the function π(s) is defined as:

The value of the constant parameter k can be calculated by performing the condition that the discriminant of the expression equation (14) under the square root is equal to zero.Hence,we obtain it as:

where

with D>P,2DP=|β|,D2+P2=ε+γ.When the individual values of k are given in equation(15)are substituted into equation (14),the eight possible forms of π(s) are written in the following forms:

Even π(s) have eight different values,but according to NU method,we select only one of them such that the functionτ(s)=(s)+2π(s) has the negative derivative and a root on the interval (0,1),that is,τ′ (s)<0and τ(s)=0,s ∊(0,1).Noticing that the other forms have no physical meaning,we will take:

After using the following relations:λ=k+π′(s) and(n=0,1,2,….)[13],we obtain λ as:

and

where n is the radial quantum number (n=0,1,2,….).After comparing equation (19) with equation (20),we obtain the following relation:

where

By inserting the expression D into equation(21)we obtain

After inserting the equations (11) and (22) into equation (23)for energy level equation,we obtain it as:

根据我国个人所得税征收的相关规定，对员工所得按当月收入（年终奖金单独计算税率）扣去免征额、养老保险费、医疗保险费、失业保险费和公积金等，以剩下的应税工资实行九级累进税率计算个人所得税。所以，企业完全可以通过几种方法来减少员工的个税缴纳，同时又不降低员工的实际收入。

By applying the NU method,we can obtain the radial eigenfunctions.After substituting π(s) and σ(s) intosolving the order differential equation,one can find the finite function Φ(s)and ρ(s)in the interval (0,1) it is easily obtained:

According to the relation χ(s)=Φ(s)y(s) [13],we obtain the radial wave functions as:

where Cnlis the normalisation constant.By using the normalisation condition,we obtain Cnlas:

where F(a,b;c;z) is the hypergeometric function.

3.Results and discussion

3.1.Particular cases

In this part,we discuss the results by investigating the expression of analytically obtained energy level equation (24) for this potential based on some special cases:

(i)By choosing the parameters of GTHP aswe obtain the energy spectrum equation of the generalised Woods-Saxon potential:

(ii) By considering W=0 and xe=0 in equation (29),we obtain the energy spectrum equation for the standard Woods-Saxon potential,as follows:

Here,C0=A0+A1+A2=[40,41],whereα=

(iii) By taking the parameters of GTHP as V3=-V1=C and V2=B,the energy spectrum equation of the Rosen-Morse potential is obtained as:

From the above expression,when l=0,the energy spectrum is in good agreement with the result in [46,47]

(iv) By taking the parameters of GTHP asand 2α=we obtain the energy spectrum equation of the Manning-Rosen-type potential as follows:

(v) By choosing the parameters of GTHP asandb=eδre+1,we obtain the following energy spectrum equation for the improved Rosen-Morse potential (the generalised Morse-type potential):

From the above expression,we obtain the same expression equation (42) of [70] with a0=A0+A1+A2,a1=-2(A1+2A2),a2=4A2andeαre+1=b.

And finally,from the expression equation (35),when considering l=0,we get the same expression as in [56]:

(vi)By choosing the parameters of GTHP V1=δ2D,V2=-2δσD and V3=σ2D,we obtain the energy spectrum equation for the Schiöberg potential,as follows:

Here

From the expression equation(37),we obtain the same expression equation(42)of[70]with a0=C0,a1=-C1,a2=C2,De=D(δ-σ)2andeαre+1=

(vii)By taking the parameters of GTHPV1=for energy spectrum equation of the four-parameter exponential-type potential,we have

(viii) By choosing the parameters of GTHPwe obtain the energy spectrum equation for the Williams-Poulios-type potential as follows:

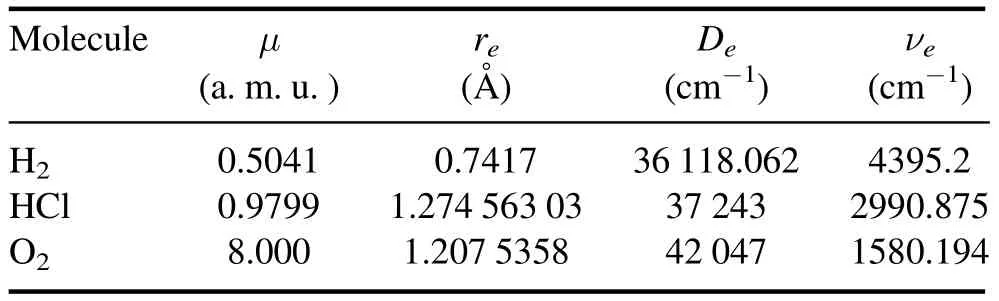
Table 1.Spectroscopic molecular parameters for H2,HCl,O2 diatomic molecules.

(ix) When α is chosen as much smaller than one,the allowed values of the energy level equation of the equation (24) are defined as follows:

for small values of n and l.

Finally,using the following transformations E-Mc2→Enland E+Mc2→2μc2,we obtain the energy level equation of equation(24)for the non-relativistic case,as follows:

and this result are same as the result obtained in[83].When α is much smaller than unity then the allowed values of the energy spectrum become

for small values of n and l,whereis the classical frequency of oscillation about the minimum point,r=re.Here,the first termis the minimum value of GTHP; the second term is the energy levels of the harmonic oscillator; the third term is the energy levels of rotational energy corresponding to a fixed distance between atoms and the fourth term is the energy levels of anharmonic correction.

3.2.The bound state energy eigenvalues and lowest excitation in diatomic molecules

Spectroscopic parameters of the diatomic molecules H2,HCl and O2are given in table 1,which are taken from[88,89].Based on the experimental values such as the dissociation energy De,the equilibrium bond length re,and the equilibrium vibrational frequency νe,the potential parameters V1,V2,V3and the screening parameter α can be defined by using the expressions (S19),(S20),(S24),and(S28) in4.

By using these parameters,we present the potential energy curves calculated for H2,HCl,O2diatomic molecules,see figure 1.Further,we can easily calculate the bound state energy eigenvalues for the diatomic molecules H2,HCl,O2at n and l quantum states by using theexpressions of the Schrödinger molecule andEnbl=EnRl-Mc2expression of the binding energies KG molecule [2],see table 2.The obtained eigenvalues of the HCl diatomic molecule are in good agreement with experimentally reported values in [90].

While we compare the lowest excitation energies for diatomic molecules,the obtained results are in perfect agreement with the sophisticated high-resolution measurements,see table 3.Although the six parameters Lennard-Jones potential model is a little bit more accurate than GTHP,the fact that GTHP has four parameters is a great advantage for easier modelling of physical systems.Generally,the obtained results allow one to tune and optime the potential concerning its desired properties in atomic,molecular,chemical,condensed matter and high energy physics applications.

4.Concluding remarks

In this study,we proposed a new potential model,which holds numerous important physical potentials.Next,the bound state solution of the radial KG equation with this potential is examined analytically within the framework of the NU method.It is also presented that the energy eigenvalues are sensitively associated with potential parameters for quantum states.GTHP and its obtained energy eigenvalues are in remarkable overlap with the reported results in some cases,so this potential model is a desirable candidate for displaying multiple quantum systems concurrently.For more specific cases,GTHP was used to study for modelling several diatomic molecules,and the study showed that the good agreement between the lowest rotational ΔE(l)and vibrational ΔE(n) excitation energies and the experimental of H2,HCland O2diatomic molecules.In view of the simplicity and accuracy,our work provides additional physical insights about the systems and sheds some light on this potential’s representative power.

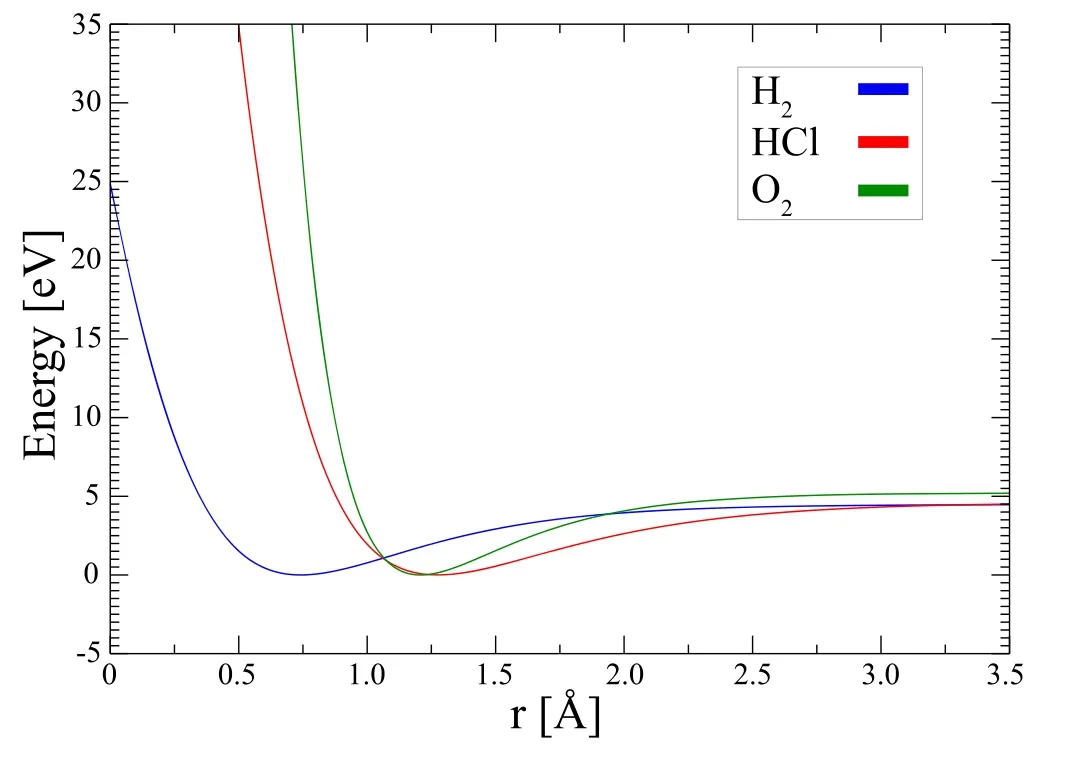
Figure 1.Potential energy curves of the diatomic molecules H2,HCl and O2 as a function of the interatomic distance.

Table 2.The bound state energy eigenvalues of the Schrödinger molecule and=EnRl-Mc2 of the Klein-Gordon molecule in the GTHP calculated using equation (42) and equation (24) for several n and l,respectively.

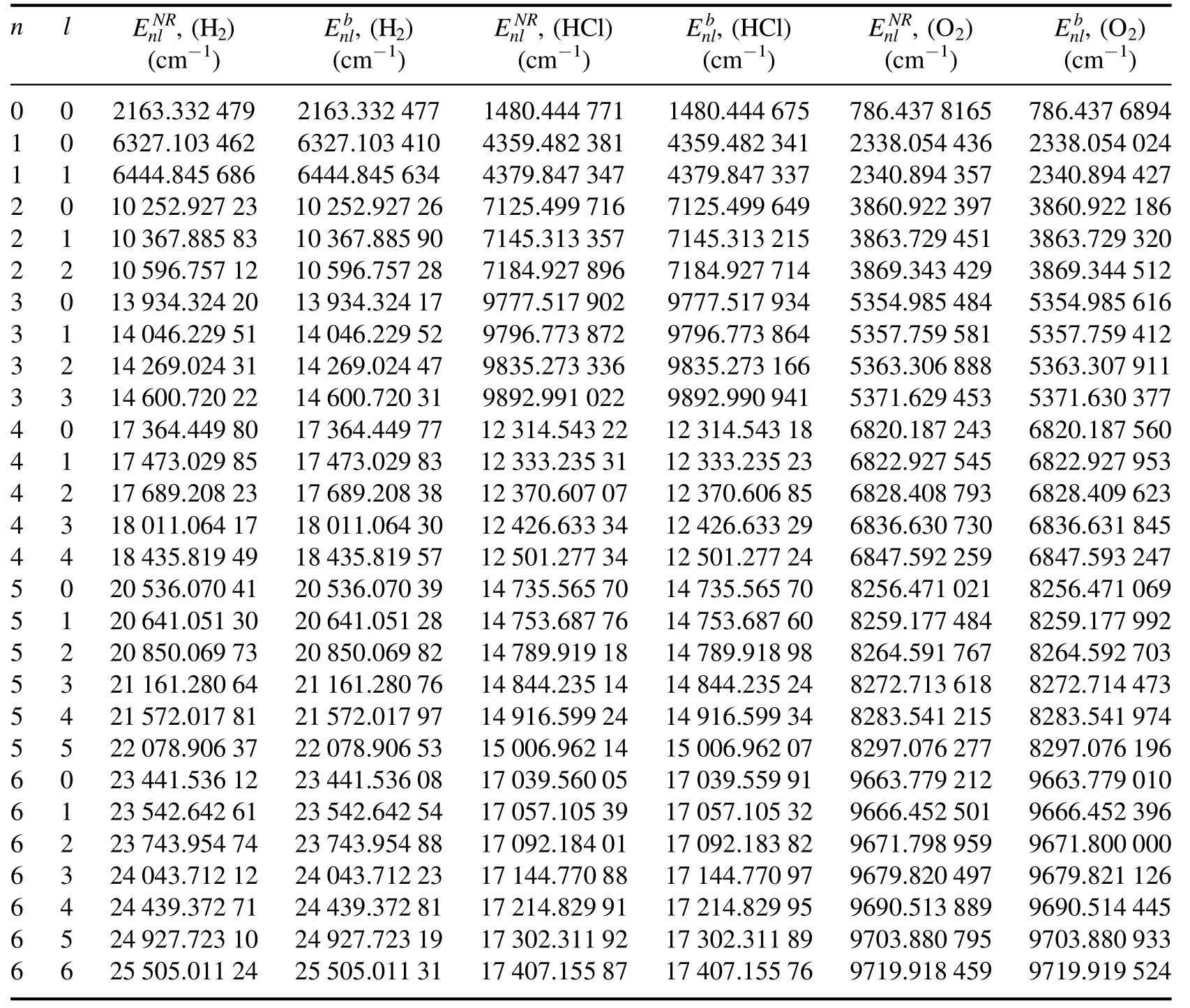
Table 2.The bound state energy eigenvalues of the Schrödinger molecule and=EnRl-Mc2 of the Klein-Gordon molecule in the GTHP calculated using equation (42) and equation (24) for several n and l,respectively.

nlE,Hnlb(2)(cm-1)(cm-1)(cm-1)(cm-1)(cm-1)(cm-1)0 02163.332 4792163.332 4771480.444 7711480.444 675786.437 8165 786.437 6894 1 06327.103 4626327.103 4104359.482 3814359.482 3412338.054 436 2338.054 024 1 16444.845 6866444.845 6344379.847 3474379.847 3372340.894 357 2340.894 427 2 0 10 252.927 23 10 252.927 267125.499 7167125.499 6493860.922 397 3860.922 186 2 1 10 367.885 83 10 367.885 907145.313 3577145.313 2153863.729 451 3863.729 320 2 2 10 596.757 12 10 596.757 287184.927 8967184.927 7143869.343 429 3869.344 512 3 0 13 934.324 20 13 934.324 179777.517 9029777.517 9345354.985 484 5354.985 616 3 1 14 046.229 51 14 046.229 529796.773 8729796.773 8645357.759 581 5357.759 412 3 2 14 269.024 31 14 269.024 479835.273 3369835.273 1665363.306 888 5363.307 911 3 3 14 600.720 22 14 600.720 319892.991 0229892.990 9415371.629 453 5371.630 377 4 0 17 364.449 80 17 364.449 77 12 314.543 22 12 314.543 18 6820.187 243 6820.187 560 4 1 17 473.029 85 17 473.029 83 12 333.235 31 12 333.235 23 6822.927 545 6822.927 953 4 2 17 689.208 23 17 689.208 38 12 370.607 07 12 370.606 85 6828.408 793 6828.409 623 4 3 18 011.064 17 18 011.064 30 12 426.633 34 12 426.633 29 6836.630 730 6836.631 845 4 4 18 435.819 49 18 435.819 57 12 501.277 34 12 501.277 24 6847.592 259 6847.593 247 5 0 20 536.070 41 20 536.070 39 14 735.565 70 14 735.565 70 8256.471 021 8256.471 069 5 1 20 641.051 30 20 641.051 28 14 753.687 76 14 753.687 60 8259.177 484 8259.177 992 5 2 20 850.069 73 20 850.069 82 14 789.919 18 14 789.918 98 8264.591 767 8264.592 703 5 3 21 161.280 64 21 161.280 76 14 844.235 14 14 844.235 24 8272.713 618 8272.714 473 5 4 21 572.017 81 21 572.017 97 14 916.599 24 14 916.599 34 8283.541 215 8283.541 974 5 5 22 078.906 37 22 078.906 53 15 006.962 14 15 006.962 07 8297.076 277 8297.076 196 6 0 23 441.536 12 23 441.536 08 17 039.560 05 17 039.559 91 9663.779 212 9663.779 010 6 1 23 542.642 61 23 542.642 54 17 057.105 39 17 057.105 32 9666.452 501 9666.452 396 6 2 23 743.954 74 23 743.954 88 17 092.184 01 17 092.183 82 9671.798 959 9671.800 000 6 3 24 043.712 12 24 043.712 23 17 144.770 88 17 144.770 97 9679.820 497 9679.821 126 6 4 24 439.372 71 24 439.372 81 17 214.829 91 17 214.829 95 9690.513 889 9690.514 445 6 5 24 927.723 10 24 927.723 19 17 302.311 92 17 302.311 89 9703.880 795 9703.880 933 6 6 25 505.011 24 25 505.011 31 17 407.155 87 17 407.155 76 9719.918 459 9719.919 524 nlNR(2)E,H nlb(2)E,HCl nlNR ()E,HCl nlb ()E,O nlNR(2)E,O

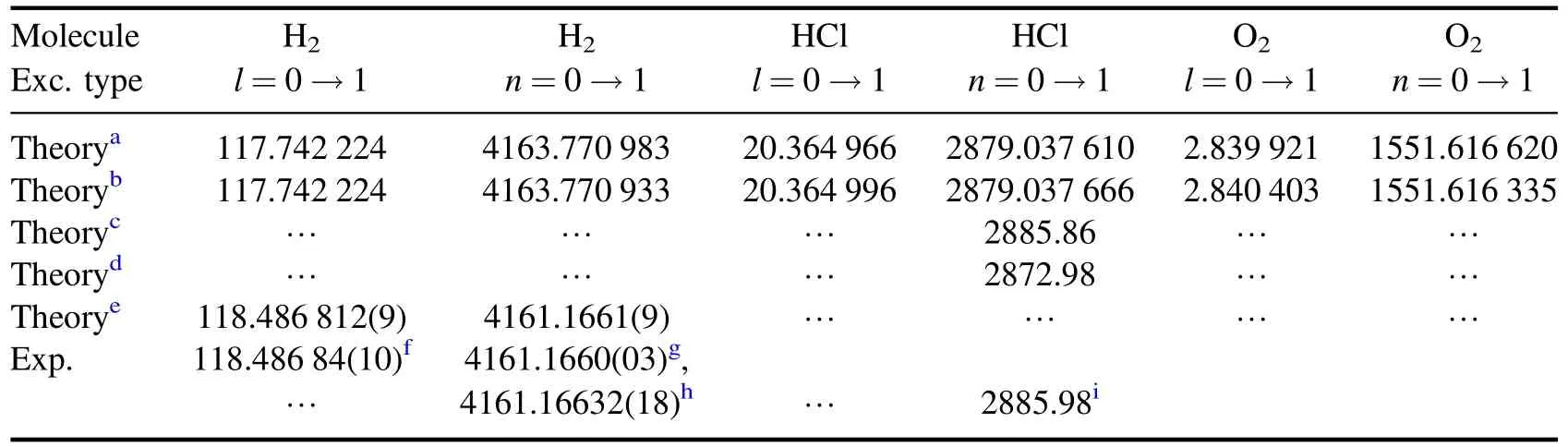
Table 3.The lowest rotational ΔE(l) and vibrational ΔE(n) excitation energies,all values in cm-1.

Acknowledgments

We thank Wolf Gero Schmidt for his valuable intellectual comments and discussion.

ORCID iDs