基于优化经验模态分解和最小二乘支持向量机的边坡位移预测
2023-09-27易智文
易智文
(萍乡市山口岩水利枢纽管理中心,江西 萍乡,337000)
0 前言
水库边坡滑坡是普遍存在的地质灾害,严重威胁库区内人民正常的生产生活[1]。为降低滑坡灾害风险,有必要开发相应的预警预报系统。受地质结构、气候条件等影响,边坡位移时间序列具有显著的非线性非稳态特征[2],若能表征这种非线性演化规律,则有助于实现位移时序的精准预测。
目前,常用的边坡位移预测方法可分为数学统计模型和机器学习模型。数学统计模型包括灰色预测模型、自回归模型等[3]。机器学习模型近年来得到众多学者青睐,常用的方法包括神经网络模型、支持向量机模型、长短期记忆神经网络模型、循环神经网络模型、随机森林模型等[4]。通过这些方法,研究者们取得了许多卓有成效的成果,但仍存在不足,如仍难以反映位移时序的非线性特征。一些学者将信号分解方法嵌入预测模型以解决上述问题,常用的方法包括小波分析、经验模态分解、变分模态分解等[5],但这类方法分解结果随机性较大,误差较高,难以赋予分量实际物理意义。
基于此,本文引入经软筛分停止准则优化后的经验模态分解,结合最小二乘支持向量机,实现非线性位移时序精准预测。该模型首先自适应地将位移-时间曲线分解为若干分量,采用K-means 法将其聚类为趋势性位移、周期性位移和随机性位移。而后,再分别采用最小二乘法和LSSVM 模型对这3 种位移分别拟合预测。最后,累加求和3 种预测位移,即可得到累计位移预测值。通过对山口岩水库监测位移进行预测,发现SSSC-EMD-LSSVM 模型预测效率和精度高,是一种可靠的非线性位移时序预测模型。
1 方法与原理
1.1 基于软筛分停止准则的经验模态分解
经验模态(Empirical mode decomposition,EMD)分解[6]是一种自适应信号处理方法,可高效、精确地处理非线性非平稳数据,故被广泛应用于各个领域。经验模态分解不受基函数约束,可将处理对象分解成不同尺度、相互独立的本征模态函数(Intrinsic mode function,IMF),弥补了傅里叶变换和小波变换的局限性。在分解过程中,本征模态函数需严格满足2 个条件:①对于整个时间序列,函数局部极值点和零穿越点数目相等或最多相差1 个;②对于任意时间序列,函数局部最大值点连成的上包络线和最小值点连成的下包络线均值为零。假定有一组初始时间序列x(t),EMD 分解过程如下:
(1)寻找局部极大值和极小值点,采用三次样条函数进行衔接,计算上包络线emax(t)和下包络线emin(t)的平均值m(t),计算公式如下:
(2)将初始时间序列x(t)与均值m(t)相减,得到差值h(t),见式(2)。若差值h(t)不满足本征模态函数基本条件,则重复上述步骤。若差值满足条件,则将h(t)作为第1 个本征模态分量IFM1,记为C1(t),将初始时间序列x(t)与该IMF 的差值作为剩余分量,记为r1(t)。
(3)将剩余分量r1(t)作为新的时间序列,对其重复步骤(1)~(2),即可得到本征模态分量IMF2,IMF3,…,IMFn,和1 个最终剩余分量rn(t)。根据上述分解过程,初始时间序列x(t)可表示为:
包络曲线拟合参数、边界条件参数和筛分停止标准参数直接影响分解精度以及效率。目前,针对包络曲线和边界条件参数已开展大量工作,少有研究报道了筛分停止准则参数的优化选取方法。在EMD 分解过程中,若筛选迭代次数太少,即“欠筛”,则可能导致模态分量包含过多单分量信号;若筛选迭代次数过多,即“过筛”,则使得模态分量包含互不相关的故障信号。因此,以往的研究常预先设置筛分阈值,但这一过程严重取决于研究者的经验,可能会导致不准确的分解结果。彭丹丹等[7]提出了一种软筛分停止准则,可以自适应优化选取筛分参数,在一定程度上弥补了上述不足。
基于软筛分停止准则的经验模态分解考虑整体能量特性和局部冲击特性,首先需要定义目标函数fik描述包络均值信号,如下式:
式中:均方根RMSik和超峭度EKik可分别由式(6)和(7)计算:
式中:n 为采样点,总数由Ns表示;mik(t)为第i 个IMF 经过k 次筛分后的包络线的均值;为mik(t)的算术平均值。
根据既定目标函数,提出启发式机制自适应地确定每次筛分过程的最优(或次优)筛分迭代次数,评价指标定义为初始判断系数P1、过程判断系数P2和结果判断系数P。软筛分停止准则流程如下:
(1)预设最大筛分迭代次数Imax,令第i 个IMF 分量经k-1 次迭代运行后得到的平滑信号hik(t)等于ri(t)。其中,ri(t)表示初始时间序列x(t)减去第i 个分量ci(t)后的残余项。而后,令目标函数fik、初始判断系数P1及迭代次数k 均设置为0。其中,P1表示为fik-1小于fik时,输出为1,则进入步骤(2)。
(2)令f=fik,P0=P1,k=k+1,用hik-1计算mik(t),再将hik-1(t)减去mik(t)得到hik(t)。而后,计算fk,若fik〉f,则P1=1,否则令P1=0,P=P0+P1,进入步骤(3)。
(3)判断是否符合筛分停止的条件:①极值点个数和零点个数相差不超过1;②fik-2〈fik-1且fik-1〈fik。若不满足条件,则返回步骤(2);若满足条件,则进入步骤(4)。
(4)对比筛分次数k 和预设筛分最大次数Imax。若k〈Imax,则将hik(t)输出为第i 个模态分量IFMi,筛分结束;若k〈Imax,则进入步骤(5)。
(5)判定结果判断系数P,若P〈2,则返回步骤(2);若P≥2,则将hik-2(t)输出为第i 个模态分量IFMi,筛分结束。
基于启发式机制的筛分停止准则能够自适应确定最优迭代次数,避免了人为干扰,解决了“欠筛”和“过筛”问题,提高了分解效率和精度。因此,本文采用经过软筛分停止准则优化后的经验模态分解(SSSC-EMD)对位移时间序列进行分解。
1.2 最小二乘支持向量机
最小二乘支持向量机(Least squares support vector machine,LSSVM) 是一种改进支持向量机(Support vector machine,SVM)[8],不仅能够解决SVM 存在的二次回归的问题,还能提高计算效率和预测精度。LSSVM使用不同的最优目标函数,引入平等约束,并采用平方误差替换原始损失函数以及控制计算数量,整体结构具有样本小、风险小的特点。LSSVM 具体实现流程如下:
假设样本集长度为l,样本集T=({xi,y)i} (i=1,2,…,l),输入量为xi∈Rn,输出量为yi∈R。采用非线性函数φ(x)将样本集映射至高维空间,则最优线性回归函数表达式为:
式中:w 为权向量;b 为偏置量。
与VSM 不同的是,LSSVM 基于结构风险最小原则,将误差平方ξi作为模型的损失函数,将约束条件转换为等式约束,则LSSVM 问题的目标函数J 为:
式中:ξi为松弛因子;C 为正则化参数,建立拉格朗日方程优化求解:
式中:ai为拉格朗日乘子。基于线性方程条件,对L(w,b,ξ,a)求各阶偏导,令各偏导分量为0 并代入式(10),消去w 和ξ 项,得到b 和a:
式中,I 为l 阶单位矩阵,y=[y1,y2,…,yl]T,H=[1,2,…,l]T,a=[a1,a2,…,al]T。K 为核函数,满足Mercer 条件,本次研究采用径向基核函数(RBF):
式中:σ 为核函数宽度。将高维特征空间中的点积运算替换为原空间中的核函数,得到LSSVM 回归函数为:
惩罚系数ξ 和核函数宽度σ 直接影响LSSVM 回归模型的精度。为此,本文采用交叉验证法进行寻优。
1.3 边坡位移预测流程
根据基于软筛分停止准则的经验模态分解和最小二乘支持向量机,对边坡位移时间序列进行预测,具体流程见图1。
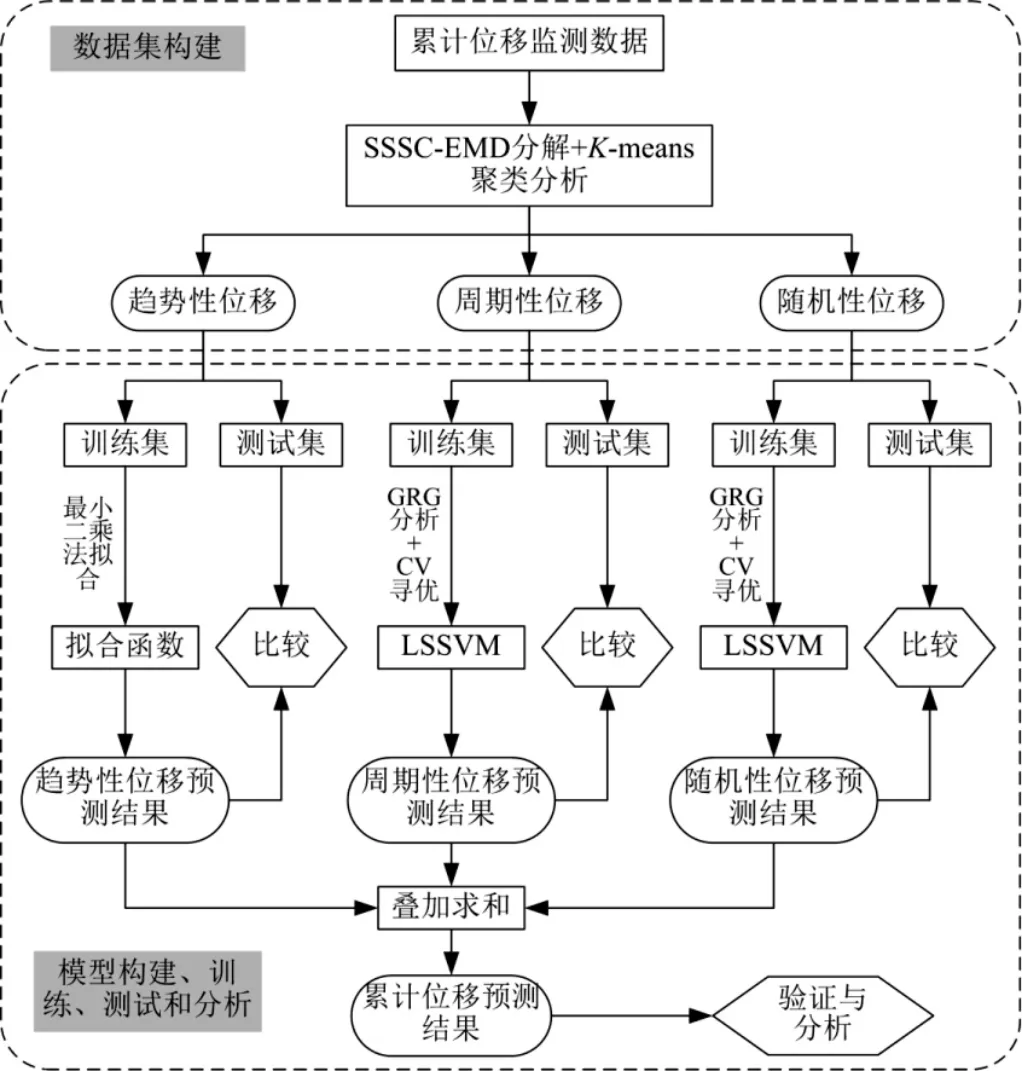
图1 基于SSSC0-EMD 和LSSVM 的位移预测流程图
(1)采用SSSC-EMD 自适应分解位移-时间曲线。一般而言,边坡位移由趋势性位移、周期性位移和随机性位移组成。残余分量与趋势项对应,IMF 分量与周期性位移和随机性位移对应。需要指出的是,若分解出的IMF 数大于所需变量数,则采用K-means 法进行分类,然后将同一类分量叠加求和,赋予其物理意义(即周期项或随机项)。
(2)分别在趋势性位移、周期性位移和随机性位移内划分训练集和测试集。
(3)采用最小二乘法拟合趋势性位移,输出位移预测结果,比较预测值与实测值。
(4)采用灰色关联分别寻找周期性位移集和随机性位移集的输入历史序列数和位移预测数据点数。而后,建立LSSVM 模型,应用交叉验证进行参数寻优。最后,按照既定比例不断迭代计算,建立效果最好的预测模型。将测试集输入至对应的预测模型,得到位移预测结果,比较预测值与实测值。
(5)将各预测位移分量累加求和,实现边坡位移预测。
为评价模型的预测精度,引入均方根误差(RMSE),平均绝对误差(MAE),判定系数(R2):
式中:yi为实际监测位移;为位移预测;为实际监测位移均值。
2 工程实例分析
2.1 工程背景
山口岩水利枢纽地处江西省萍乡市芦溪县,位于赣江支流袁河上游。发电厂房位于下游河道约200 m处,厂址区自然边坡坡度约25° ~35°,坡角约50°。运营过程中,厂房边坡出现显著蠕滑裂缝,极易诱发滑坡灾害。因此,亟待开展滑坡位移监测、预测。
严格按照《混凝土坝安全监测技术规范》(DL/T5178)采用TS15 全站仪开展边坡位移监测,对W14测点59 个月(2018 年5 月至2023 年3 月)的位移监测数据进行研究。W14 测点布置图如图2 所示,位移监测数据如图3 所示。训练集和测试集的划分严重影响模型结果,研究表明训练集长度越长,测试精度越高,但相应的计算时间更长。为协调计算精度和时间,依据前人研究经验[9],将训练集与测试集的比例设置为8:2,即前47 个月(2018 年5 月至2022 年3 月)的数据作为训练集,后12 个月(2022 年4 月至2023 年3 月)的数据作为测试集。

图2 监测点布置图

图3 W14 测点累计位移
2.2 位移分解
采用SSSC-EMD 分解位移时间序列,结果如图4所示。从图中可知,W14 测点累计位移时间序列共分解出2 项高频分量IMF1和IMF2,1 项低频分量IMF3,1 项残余分量r。由于IMF 分量数为3,故采用K-means 将其聚类为2 类,选用Sqeuclidean 作为聚类距离计算方法。聚类轮廓系数是表征聚类效果的指标之一,聚类轮廓系数越高,分量之间相关程度越高。根据计算结果可知,若将IMF1和IMF2聚为一类,MF3单独为一类,聚类轮廓系数为0.73,表明聚类效果较好[10]。因此,将高频分量IMF1和IMF2累加求和,作为周期性位移;将IMF3作为随机性位移;将残余分量r 作为趋势性位移。

图4 W14 测点累计位移SSSC-EMD 分解结果
2.3 位移预测
2.3.1 趋势性位移预测
结合图5 可知,随着时间的推移,残余分量r 表现为单调递增的趋势,故可采用最小二乘法对其进行拟合预测。结果表明,3 次多项式拟合结果精度最高,RMSE 为0.005 mm,MAE 为0.004 mm,R2达1.00。
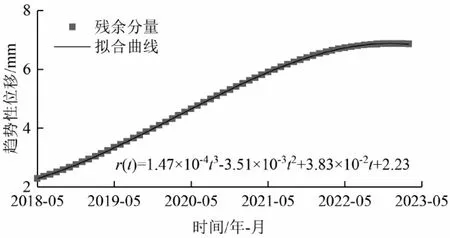
图5 趋势性位移预测结果
2.3.2 周期性位移预测
建立LSSVM 模型预测周期性位移时间序列。首先,采用灰色关联法确定历史序列数为5,位移预测数据点数为1,再运用交叉验证法对模型参数寻优,C=1.26,σ=1.22,最后训练模型并输出预测值。预测结果如图6 所示,通过与监测结果比较可知,RSME 为0.037 mm,MAE 为0.033 mm,R2为0.96。

图6 周期性位移预测结果
2.3.3 随机性位移预测
建立LSSVM 模型预测随机性位移时间序列。首先,采用灰色关联法确定历史序列数为6,位移预测数据点数为1,再运用交叉验证法对模型参数寻优,C=1.05,σ=1.93,最后训练模型并输出预测值。预测结果如图7所示,通过与监测结果比较可知,RSME 为0.018 mm,MAE 为0.017 mm,R2为0.99。

图7 随机性位移预测结果
2.3.4 累计位移预测
根据上述分解流程可知,累计位移为趋势性位移、周期性位移和随机性位移之和。因此,将趋势性位移预测值、周期性位移预测值和随机性位移预测值累加求和,即可得到累计位移预测值,结果如图8 所示。通过与实测值对比可知,位移预测模型的RSME 为0.045 mm,MAE 为0.039 mm,R2为0.97。

图8 累计位移预测结果
2.4 模型比较
本节同时也采用BP 神经网络和传统最小二乘支持向量机回归模型(LSSVM)对累计位移预测,以分析SSSC-EMD-LSSVM 模型的优越性。为避免不同寻优方法的影响,这2 种模型的超参数也采用交叉验证法确定。
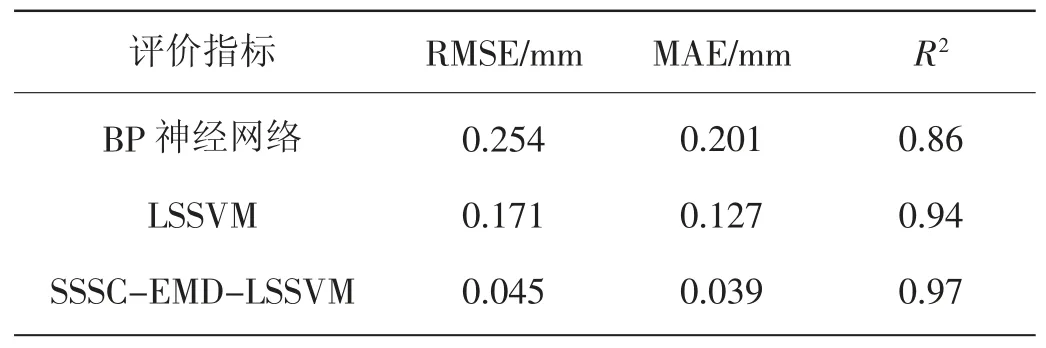
表1 不同模型预测精度比较结果
3 结论
(1)针对非线性位移时间序列难以准确预测的难题,本文结合优化经验模态分解和最小二乘支持向量机,将时间序列分层分解为多个分量,分别预测后再叠加重构,即可得到累计位移预测值。
(2)以山口岩水库为例开展位移时间序列预测。与传统BP 神经网络和LSSVM 模型相比,本文提出的SSSC-EMD-LSSVM 模型预测精度更优,RMSE 为0.045 mm,MAE 为0.039 mm,R2为0.97,说明这是一种性能较好的非线性位移时间序列预测模型。
