基于剪切波变换和拟合优度检验的遥感图像去噪
2023-09-27成丽波陈鹏宇贾小宁
成丽波, 陈鹏宇, 李 喆, 贾小宁
(长春理工大学 数学与统计学院, 长春 130022)
遥感图像目前已成为人们观察、 分析世界的一种有效工具, 在各领域均广泛应用[1-3]. 遥感图像在成像过程中会受随机噪声的干扰[4-6]. 为获取尽可能真实、 清晰的遥感图像, 满足工程实践的需要, 如何在尽量不影响遥感图像原始信息的情况下有效对其进行去噪具有重要意义.
遥感图像去噪的目的是抑制和消除随机噪声, 保持图像的细节信息及良好的视觉效果. 遥感图像的稀疏表示和去噪也是对其进一步处理的基础. 经典的遥感图像去噪方法如小波变换[7-9]和复小波变换[10-11]是将噪声视为高频信号, 过滤较大的变换系数[12-13], 进而实现去噪, 但高频系数中的图像细节部分通常会与噪声一起被去除[14]. 为克服上述问题, 近年来, 剪切波变换(shearlet transform, ST)[15-16]作为一种新的多尺度分析[17-18]技术已成为该领域研究的焦点. 在频域中, 剪切波变换是逐层细分的. 因此, 剪切波是性能较优的多维函数稀疏表示方法[19], 使它在图像去噪领域有广泛的应用前景. 剪切波变换具有良好的各向异性, 可以很好地识别和分析图像的边缘和纹理信息[20]. 遥感图像含有大量的细节信息, 因此, 在遥感图像去噪中, 剪切波是一种理想的工具. 遥感图像噪声的主要来源是空气中的微小粒子, 粒子对光的透射率及其空间分布均呈高斯分布[21]. 基于拟合优度(goodness of fit, GOF)检验的图像去噪方法[22-23]利用高斯白噪声及变换系数的统计相关性估计去噪阈值, 该方法能有效去除高斯噪声. 相比于其他检验方法, Anderson-Darling(AD)检验[24]能在较小的样本条件下, 保持稳健的检验性能. 因此, 本文使用AD检验进行遥感图像的噪声识别.
针对遥感图像去噪问题, 本文提出一种基于剪切波和拟合优度检验的遥感图像去噪算法(shearlet transform and goodness of fit test, ST-GOF), 先使用剪切波变换分解含噪遥感图像, 将高频系数进行拟合优度检验, 再通过计算剪切波系数经验分布函数(empirical distribution function, EDF)和模拟高斯噪声的累积分布函数(cumulative distribution function, CDF)的统计距离获得AD检验统计量, 将统计量与阈值进行对比实现去噪. 与其他相关算法进行仿真对比实验的结果表明了本文算法在视觉和性能上的优越性.
1 剪切波变换
二维图像函数f∈L2(2)的连续剪切波变换定义为
SHψf(a,s,t)=〈f,ψa,s,t〉,
(1)



(2)
其中ψa,s,t是一个尺度、 方向及位置参数分别为a,s,t的局部性函数集合, 此时a称为尺度参数,s为剪切参数,t为平移参数.每个ψa,s,t的频域支撑区间在一个梯形对内, 该梯形对在不同的尺度参数a下关于原点对称, 其方向由剪切参数s确定.通过减小尺度参数a, 剪切波能很好地捕捉图像的轮廓与边缘信息.每个剪切波ψa,s,t在频域的支撑区间为

(3)
ψa,s,t的频域支撑区间如图1所示.
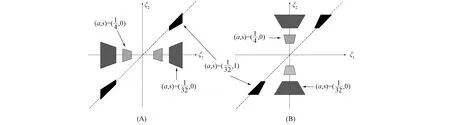
图1 剪切波水平(A)和垂直(B)频域支撑Fig.1 Horizontal (A) and vertical (B) frequency domain support of shearlet
对于给定的一张不含噪声的图像P, 基于剪切波变换对加噪图像Pnoisy的阈值去噪算法实现过程为
Pdenoise=ST-1TσSTPnoisy,
(4)
其中ST为剪切波正变换,Tσ为阈值算子,ST-1为剪切波逆变换.剪切波正变换后获得图像的高频和低频系数, 而噪声主要分布在高频系数中, 因此需对高频系数选取合适的阈值算法进行处理, 对处理后的全部系数进行剪切波逆变换得到去噪图像Pdenoise.
2 拟合优度检验
检验一个指定的样本与一套给定结果的吻合程度称为拟合优度检验, 通常通过计算检验统计量并与临界值进行比较判断样本分布是否与假设分布一致.若样本分布与假设理论分布一致, 即将观测值或数据符合指定模型或分布的情况称为零假设, 把观测值拒绝指定模型或分布的情况称为替代假设.不同方法定义了不同的检验统计量作为量化观测值与指定分布下预期值之间差异的衡量标准.
2.1 Anderson-Darling检验


(5)
其中ψ(Fr(t))是为分布函数Fr(t)的尾部赋予更多权重的加权函数, 定义为
ψ(Fr(t))=(Fr(t)(1-Fr(t)))-1,
(6)
其目的是提高检验时的灵活性.
实际计算过程中式(5)统计距离的数值表达式可简写为
τAD=-L-q,
(7)
其中:L表示给定观测值xt的大小或在拟合优度检验时分块(窗口)的大小;q定义为
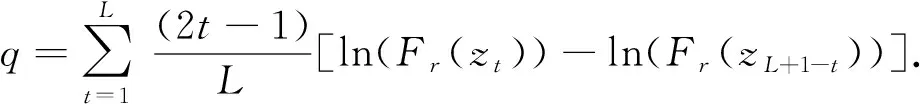
(8)
在拟合优度检验框架内, 错误拒绝候选分布的概率称为虚警概率Pfa, 定义为
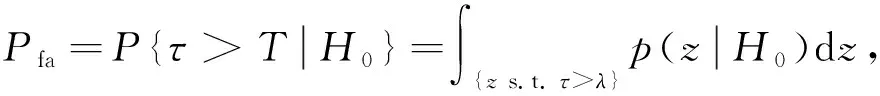
(9)
其中H0表示与噪声检测相对应的零假设.文献[25-26]给出了虚警概率Pfa对应阈值的表格.
2.2 本文算法
本文利用剪切波变换对噪声图像的剪切波子带系数进行拟合优度检验, 提出一种剪切波拟合优度检验去噪算法, 在多尺度上将信号和噪声分离为单独的系数.
令TGOF表示阈值算子, 则尺度j处的阈值Tj为

(10)

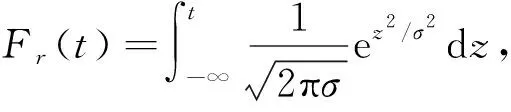
(11)


(12)
并通过
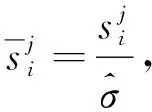
(13)

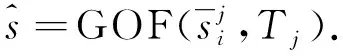
(14)
本文算法的去噪二元假设表示如下:

(15)

2.3 算法流程
本文提出的ST-GOF算法实现过程主要分为7个步骤. 图2为ST-GOF算法的实现流程.

图2 ST-GOF算法流程Fig.2 Flow chart of ST-GOF algorithm
算法1ST-GOF算法.
步骤1) 输入含噪遥感图像Pn;
步骤2) 对Pn进行剪切波变换Pn←ST(X)得到高频和低频系数矩阵;

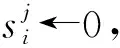
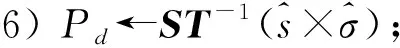
步骤7) 输出去噪遥感图像Pd.
3 仿真实验及结果分析
为验证本文算法的有效性, 选择灰度遥感图像进行主观和客观指标的评价.主观上, 通过视觉观察遥感图像的边缘显示能力, 并对比细节恢复程度等对本文算法的去噪效果进行评价; 客观上, 使用峰值信噪比(peak signal to noise ratio, PSNR)衡量本文算法的去噪效果.
3.1 图像质量评价指标
PSNR值作为图像去噪问题中的重要衡量指标, 数值越大表示去噪程度越好. 本文采用PSNR作为评价指标验证算法的优越性:

(16)
其中p(i,j)表示原始无噪声图像,d(i,j)表示去噪图像,X,Y表示图像尺寸.
3.2 实验结果与分析
本文从遥感数据集RSSCN7中选取6张大小为400×400的遥感图像Forest,Parking,Resident,Playground,Industry,Mountains作为仿真实验图像, 如图3所示. 将本文算法与离散小波拟合优度算法(DWT-GOF)、 双树复小波拟合优度算法(DTCWT-GOF)、 曲波阈值去噪算法(Curvelet)、 剪切波阈值去噪算法(Shearlet)进行对比, 5种算法均使用MATLAB R2018b实现, 计算平台为内存16 GB的计算机, 搭载处理器为Intel(R) Core(TM) i7-8750H CPU@2.20 GHz.

图3 实验采用的无噪声遥感图像Fig.3 Noise-free remote sensing images used in experiment
对比发现, 添加了标准差约为20的高斯白噪声的遥感图像接近含有真实随机噪声的遥感图像. 因此, 对实验图像分别添加标准差为10,15,20,25的高斯白噪声. 实验所得5种算法的PSNR值分别列于表1~表4. 由表1~表4可见, 本文算法在不同噪声强度下的去噪图像PSNR值均优于其他4种算法, 其中与曲波阈值算法相比平均提高2.15 dB, 与DWT-GOF算法相比平均提高1.04 dB, 与剪切波阈值算法相比平均提高0.33 dB, 与DTCWT-GOF算法相比平均提高0.23 dB.

表1 噪声标准差为10时不同算法的PSNR值Table 1 PSNR values of different algorithms when standard deviation of noise is 10 dB

表2 噪声标准差为15时不同算法的PSNR值Table 2 PSNR values of different algorithms when standard deviation of noise is 15 dB

表3 噪声标准差为20时不同算法的PSNR值Table 3 PSNR values of different algorithms when standard deviation of noise is 20 dB

表4 噪声标准差为25时不同算法的PSNR值Table 4 PSNR values of different algorithms when standard deviation of noise is 25 dB
图4为噪声标准差为25时, 实验所得5种算法的去噪图像及局部细节放大结果. 由图4可见, 本文算法的去噪效果明显优于其他4种算法, 能更好地保持遥感图像的边缘、 轮廓和特征信息. 在对局部细节进行放大时, 本文算法去噪图像的纹理更细腻, 视觉效果最优.

图4 不同算法对遥感图像的去噪及细节效果Fig.4 Denoising and detail effects of different algorithms on remote sensing images
综上所述, 针对遥感图像中的高斯白噪声, 本文提出了一种基于剪切波变换和拟合优度检验的遥感图像去噪算法, 将遥感图像的去噪转换成了一个二元假设检验问题. 首先, 利用剪切波变换在频域分解含噪遥感图像, 对分解得到的高频子带进行拟合优度检验; 其次, 通过对比检验统计量与去噪阈值分类系数, 保留期望信号系数, 实现去噪; 最后, 对系数矩阵逆归一化, 通过剪切波逆变换进行图像重建. 实验结果表明, 与剪切波阈值去噪等算法相比, 本文算法能显著提升峰值信噪比, 有较强的细节留存和边缘保持能力, 主观上也有较好的视觉效果.
