交叉航路汇聚航空器临界调配间隔研究

杜 实，初新宇

（中国民航大学空中交通管理学院学院，天津 300300）

安全是民航运输的生命线。在空管运行中，保证不同航空器之间具有一定的安全间隔是保证民航运输安全最基本的方法。现阶段，由于空中的航空器日益增多，航路资源日益紧张，在保证安全间隔的前提下，尽可能提高空域利用效率，以适应不断增长的航班量需求，缩小实际运行时航空器的间隔是最直接的方法。由于空中交通具有复杂性和高速性的特点，任何一个细微的改变都可能会引起强烈的连锁反应，因此，如何在保证安全的前提下缩小航空器实际运行时的间隔是解决上述问题的关键。

在相关研究中，朱承元等[1]构建了基于辐射面的复杂度模型来表征交叉点的运行状况，并提出4 种优化方案：环岛或类环岛、先行逐级汇聚、分流式立交桥、纯高度立交桥来提高航路交叉点流量。陶媚等[2]基于管型航路（TUBE）理论设计交叉航路，使汇聚的交通流集中到管型航路中，再根据航班的目的地对航班进行分流，极大减少了管制员的工作负荷。戴福青等[3]通过对不同角度下交叉航路的航班进行分析，发现其飞行时间和油耗与航路交叉角存在非线性关系，并通过拟合得出最优角度。在上述研究中：环岛等4 种优化方案设计比较精细，但比较复杂，且各种立交桥模式需要占用较大的空域，实际运行时由于受到各种限制区、危险区、禁区以及空军活动的影响，实施起来较为困难；基于TUBE 理论的设计中将交叉航路简化为单一管道，使航空器过于集中，且细小管道内的航空器处理难度较大；对于角度拟合寻优的研究方法，在实际运行中由于航路结构十分复杂，加之各种限制因素，航路的交叉角很难改变，因此应用起来困难和限制较大。

文献[4-6]对航路交叉点的研究主要集中在碰撞风险、容量评估和交叉角与航空运行相关参数之间的关系上，具有很强的理论性，对于管制规则和管制间隔标准的制订是非常必要的，但在实际情况中往往条件不允许，短期内较难得到实践。

受中国人口与城市分布和经济发展的影响，东部地区的单位空域面积内航路点多、航路结构复杂，可用于机动调配的空域少，且航班流量大，在某些汇聚航路交叉点处，因流量过大导致汇聚点处必然产生系统性、结构性的冲突。当航空器汇聚时，由于考虑到主要航路上的航空器最小安全间隔问题，管制员只能选择指挥部分航班避让，这就使得航班飞行时间增加，燃油消耗增大。

本文将根据无信号交叉口理论，结合中国航空器实际运行情况，在华东地区空中交通管理局（简称华东空管局）上海情报中心实际航班轨迹数据分析处理的基础上，估计航空器临界调配间隔，来减少管制员对航空器高度层的调配，进而减少管制员的工作负荷，并减少航空器的等待、绕航和过多的高度变化，从而提升航空公司的经济效益。

1 无信号交叉口理论

在交通流理论[7]中，交叉口的交通流运行规律取决于是否有信号灯，而对于空中交通来说，由于航空器在空中等待不能像汽车一样停下不动，而是表现为盘旋绕飞，或通过改变高度层进行避让。对于管制员而言，在汇聚航路交叉点处，航空器能否从次要航路进入主要航路，取决于管制员对主要航路和次要航路上航空器间隔的判断。对于有信号灯的交叉路口，何时停或何时行，是有固定时间设定的。因此，汇聚航路交叉点处的交通流特性应当适用无信号交叉口理论。

1.1 可插车间隙理论

可插车间隙理论是无信号交叉口理论的重要组成部分，在地面道路交通中对于无信号交叉口，交叉点处没有信号控制，驾驶人员需要根据其经验决定何时进入交叉口是安全的，所寻求的进交叉口的空当称为可插车间隙，这个间隙既可以是时间也可以是距离。由于各运载工具具有不同的速度，所以间隙一般用时间进行度量。对于空中交通而言，航空器能否从次要航路并入主航路主要是依靠管制人员的判断，飞行员类似于执行命令的电脑，不具有决策权，因此可以将管制员类比为公路中的汽车驾驶员（但比驾驶员掌握更多、更全面的信息）作为研究的行为对象，可插车间隙在本文中也可以称为“管制员不作为间隔”。

1.2 相关概念与假设

在汇聚航路结构中，将主次航路上航空器之间的间隔拆分为非冲突情况与冲突情况，如图1（a）和图1（b）所示。在非冲突情况下，管制员无须对航空器下达间隔调配指令；在冲突情况下，管制人员则需要通过一些间隔调配的方法对其中一个航空器的运行状态进行调整。

图1 汇聚航路航空器Fig 1 The aircraft of convergence route

图1 中，航路A 为主要航路，航路B 为次要航路，主次航路上各有一架航空器a 和航空器b 在同一高度飞行层，航空器a 试图从次要航路进入主要航路。当航空器b 位于图1（a）位置时，管制员认为两架航空器保持当前飞行状态继续飞行可以保证足够的安全间隔，因此航空器a 可以汇入主航路，不需要调配，将该情况定义为非冲突情况；当航空器b 位于图1（b）时，管制员认为两架航空器保持当前飞行状态继续飞行不能保证足够的安全间隔，需要调配，将该情况定义为冲突情况。只有当管制员认为汇聚航路上的航空器处于非冲突情况时，管制员才不会对航空器的间隔进行调配。航空器a 与航空器b 之间的间隔应当始终大于中国民用航空局规定的最小间隔标准，且管制员在判断航空器是否处于冲突情况时，航空器对的间隔应当远远大于最小间隔标准，以确保有足够的调配时间。

对于汇聚航路而言，两条航路上的航空器实际间隔并不能真实地反映两架航空器是否处于冲突状态或有潜在冲突的情况，如图2 所示。在距离汇聚点较远时，航空器对的侧向间隔1 非常大，但随着航空器的持续前行这一间距逐渐变小，当距离汇聚点较近时，侧向间隔2 将小于规定值，航空器处于冲突状态。

图2 不同位置航空器实际间隔Fig.2 Actual separation of aircraft at different positions

为了更好地将航空器间隔与冲突情况进行关联，本文引入“等价前后间隔”的概念。从某条航路上的航空器位置处作另一条航路的垂线，垂足即为该航空器在另一条航路上的投影，垂足与该航路上的另一架飞机的间隔即为等价前后间隔，如图3 所示。

图3 等价前后间隔Fig.3 Equivalent anterior and posterior separation

引入等价前后间隔主要有以下优点：

（1）在航空器间隔的分析研究过程中能够更加直观地得出航空器是否有潜在冲突的结论；

（2）航路夹角较小时，在航空器速度差异不大的情况下，航空器距离汇聚点的位置会影响航空器实际间隔，但对等价前后间隔值影响较小，如图4 所示。

图4 前后等价间隔与位置关系Fig.4 Relationship of equivalent anterior and posterior separation and position

图4 中，射线OB1与OA1代表两条汇聚航路，A1、A 分别代表次要航路上航空器某段时间前和当前的位置，B1、B 分别代表主要航路上航空器某段时间前和当前的位置，A1′和A′代表次要航路上航空器在主要航路上对应的投影。假设航空器飞行速度相等，在相同的时间内，两架航空器均飞过了距离x，分别到达位置A 和位置B，航路角为α，通过查找航图可知，A、B、O点的经纬度坐标由航迹数据可知，距离可求。经计算OA 距离为a，OB 距离为b，BB1=AA1=x，可得

管制部门将航路角α ＜45°的交叉航路定义为同航迹[8]，但在国内空管实践当中，航路角满足15°＜α ＜30°的相交航路一般称为汇聚航路，由式（1）和式（2）可知：当航路角α→15°时，limα→15°cos α=0.97，limα→15°（xx cos α）=0.03x；当航路角α→30°时，limα→30°cos α=0.87，limα→30°（x-x cos α）=0.13x。因此，对于汇聚航路，在航空器飞行速度相同的情况下，不同位置处的等价前后间隔的变化量仅为飞行距离的3%～13%。

在汇聚航路交叉点处，把交通流按照优先权划分为主要交通流和次要交通流，或优先交通流和非优先交通流。由于空中交通与公路交通的差异，管制员不会将航路明确地分为主要航路和次要航路，因此，本文将在交叉点处没有执行避让的航空器所在航路作为主要航路，该航路上的交通流为优先交通流，另外一条航路即为次要航路，该航路上的交通流为非优先交通流。

在可插车间隙理论中，有一个非常重要的参数，即临界间隙，引入到空中交通管制中，本文将其称为临界间隔。临界间隔是指在次要航路上所有管制员在航路汇聚交叉点附近所能接受的最小间隔，当主次航路的航空器对间隔大于临界间隔时，管制员可以不对航空器进行调配。通过对大量空管运行数据进行计算分析，可估计出汇聚航路交叉点临界间隔，使管制员在保证最小安全间隔的情况下，尽可能减少管制员发布调配指令。

与空管部门规定的间隔标准不同，在实际的管制工作中，管制单位和管制员为避免出现“犯错误”的情况，因此各级管制单位会在工作中出现“层层加码”的现象，即航空器对的间隔需要数倍于间隔标准才能保证不触犯条例。基于以上描述，临界间隔的意义在于既要将过大的间隔余量压缩，同时又要保证一线管制员在工作时有足够的“安全感”，这样计算出来的结果更具有实用价值。

根据目前管制单位的相关规定，一个管制扇区的管制员有很大概率是由同一个或同一组管制教员培训的，并经过长时间的工作磨合，这些管制员的管制习惯基本相近，因此，可认为管制员的管制方式具有一致性和相似性。一致性是指管制员在任何时刻面临所有相似情况都会采取相同的决策，因此对于出现拒绝一个较大的间隙，而接受一个较小间隙的情况应当舍去[7]。事实上，这种情况在空中交通中非常常见，在空域没有限制的情况下，飞行员出于飞行安全、节油以及其他操作上的需要，通常会请示管制员能否按照自己需求改变当前飞行状态，此时管制员通常会同意飞行员的要求。

目前，中国空中交通管理的间隔调配方式主要有折线机动、盘旋等待，以此来建立侧向间隔，如图5 和图6 所示。由于空中交通的空间特性，使其比公路交通的通行维度多一维，也就是垂直维度，因此当航空器可能产生间隔冲突时，也可以通过改变高度的方式调整间隔。

图5 折线机动Fig.5 Broken line maneuver

图6 盘旋等待Fig.6 Hover waiting

2 临界间隔估计模型

2.1 概率均衡法

概率均衡法[9-10]是基于接受间隔和拒绝间隔均衡的宏观概率估计临界间隔（在当前间隔下，管制员接受航空器按照现在的飞行状态继续飞行，不加以操纵时，称该间隔为接受间隔，反之则为拒绝间隔）。依照接受间隔概率分布函数Fa（t）和拒绝接受间隔概率分布函数Fr（t），经观察得到的时间长度t 被接受的概率是1-Fa（t），“不被接受”的概率是Fa（t）；经观察得到的时间长度t 被拒绝的概率是Fr（t），“不被拒绝”的概率是1 -Fr（t）。通常情况下，Fr（t）≠1 -Fa（t），1 -Fr（t）≠Fa（t）。因为在主要交通流中的可接受间隔中不会有一个准确的实际关键间隔，事实上可接受间隔一般是大于临界间隔。

设定关键可接受间隔的概率分布函数为Ftc（t），则两航空器间隔d 被拒绝的概率Pr，tc（t）=Ftc（t），而d被接受的概率Pa，tc（t）=1-Ftc（t）。

2.2 概率均衡法的估计模型建立

概率均衡法是利用接受间隔和拒绝间隔均衡的宏观概率进行估计计算的，根据之前的研究经验[9-10]，可知均衡概率为

由于Pr，tc（t）=Ftc（t），Pa，tc（t）=1-Ftc（t），代入式（3）得到临界间隔的求解公式

对马尔可夫链和概率均衡来说，该方法可得到鲁棒性结果，这种方法是独立于任何模型假设，不需要预先假定关键间隔的分布函数，且能直接得到关键间隔的经验概率密度函数，计算过程简单且不需要迭代。

2.3 管制员决策点

航空器飞行速度快，不能原地停止，管制员不会在航空器进入交叉点时对其下达机动调整指令，通常在进入交叉点之前已经完成了机动调整动作（折线机动、盘旋，建立侧向间隔或改变高度层）。因此，将管制员下达避让指令的位置称作决策点，也可以称为等待点，这个点可以视作十字路口处的停止线。管制员在进行管制工作时，通常一条航路上的前后航空器对之间的纵向间隔一直都大于规定的最小间隔，因此管制员的决策主要集中在次要航路上的航空器与主航路上的航空器是否处于冲突情况，以此来决定是否让次要航路的航空器进行避让。

根据中国空管相关要求[11]，高度层分配按照：8 400 m以下，每300 m 一个高度层；8 400～8 900 m 每500 m一个高度层；8 900～12 500 m，每300 m 一个高度层；12 500 m 以上，每600 m 一个高度层。

由于“东单西双”高度层使用原则，航空器同向飞行时，改变高度层需要的高度改变至少达到600 m，因此只对高度改变小于600 m 的航空器视作避让航空器，但在具体计算时只要避让航空器高度变化达到或超过300 m（与该高度上的航空器没有冲突）即符合与原高度上航空器的间隔要求。

对于避让航空器即拒绝航空器，由于等价前后间隔的特点，航空器在汇聚航路的不同位置接到管制员调配指令，其等价前后间隔差异较小，因此对于在不同位置进行避让的航空器，可以直接通过等价前后间隔获取其间隔分布情况。

由于管制员在雷达屏幕上只能观察或测量航空器的实际间隔，因此通过等价前后间隔计算的临界间隔只有研究价值，但不能直接应用于实际工作。因此，需要对管制员普遍的管制习惯进行统计计算，从而找到一个较为合理的决策点。在该点处，将等价前后间隔的临界间隔通过解三角形的方法转化为航空器实际间隔的临界间隔。在实际的管制工作中，管制员在该决策点处通过比较航空器实际间隔和实际间隔的临界值来决定是否对航空器下达管制指令。

对于没有避让的航空器即为接受航空器，本文以上述决策点假定为管制员的判断点，以该位置为基准，计算航空器的等价前后间隔并得到接受间隔的分布情况。

2.4 三分法求解决策点

将每个航空器改变飞行状态的位置定义为调配点，每个管制员以及管制员每次调配时机均有所不同，且由于实际运行原因航空器并不是完全准确地位于航路上，因此，应当在航路上选取一点作为决策点，该点距离所有样本调配点的距离和应该最小，如图7所示。

图7 三分法原理Fig.7 The principle of trichotomy

由于二分法适用于单调函数，而本文所求距离和的变化为具有单峰值的非单调变化，且峰值左右两侧不对称，因此采用三分法进行求解。

获取所涉及的航路最左端和最右端坐标，并计算中点mid 坐标，紧接着计算最右端与mid 的中点mmid的坐标，设mid 到所有调配点的距离和为Pm，mmid 到所有调配点的距离和为Pmm，比较Pm与Pmm的值来判断极值点所在位置。当存在Pm＜Pmm时则说明mid 更接近极值点，保留更靠近极值点的点，重新记为mid，另一个点的坐标替换为新的端点坐标，再计算新的mid，循环该过程，直至最后一次求解时两点的距离足够近。流程如图8 所示。

图8 三分法流程图Fig 8 Flow chart of trichotomy

第i 个调配点Pi与第j 次迭代的端点的距离为

式中：xi、yi表示第i 架航空器飞行状态发生改变的位置经、纬度；xj、yj表示第j 次迭代后的端点的经、纬度；R地表示地球的平均半径。

总距离为

2.5 决策点处航空器实际间隔

图9 中，航空器飞行至决策点A 处，决策点A 距离汇聚点距离为a，航空器等价前后间隔经计算为m，则

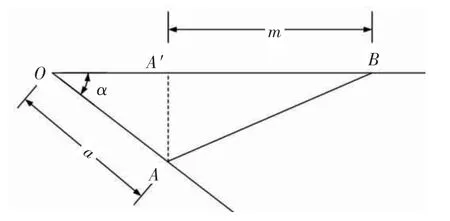
图9 航空器实际间隔Fig.9 The actual separation of aircraft

式（6）由于需要输入较多参数，在使用时较为繁琐，在得出航空器等价前后间隔后，航空器实际间隔可通过勾股定理计算其欧式距离为

由式（9）可以看出，航空器实际间隔与航路角呈正相关关系，航路角对航空器实际间隔及管制员的决策都有着重要影响。

3 算例分析

选取华东空管局上海情报中心2020 年9 月21日、10 月18 日和10 月20 日邳县附近的数据进行分析。

航空器飞行状态改变的位置分布如图10 所示。

图10 航空器飞行状态调配点Fig.10 Adjustment point of aircraft flight status

由图10 可以看出，管制员对航空器调配位置的选择较为分散，集中区不明显，这也能反映管制员的工作习惯相差较大，没有固定标准。在这种情况下，管制员在面临决策时往往会有更多的犹豫和思考时间，增加了管制员的决策时间。

通过三分法求得最合适的管制员决策点，迭代过程如表1 所示。

表1 两航路三分法迭代结果Tab.1 Iteration results of two routes based on trichotomy

迭代结束后将取最后两个端点的坐标：A470航路两点坐标为（E118.417 549 498°，N33.058 552 594°），（E118.417 587 315°，N33.058 444 557 3°）；A593 航路两点坐标为（E118.835 596 229°，N33.355 669 742 5°），（E118.835 682 071°，N33.355 573 847 3°）。A470 航路中，第1 个中点与所有调配点的距离和最小，因此选第1个中点作为A470 航路决策点；A593 航路中，第1个中点与所有调配点的距离和最小，因此也选第1 个中点作为A593 航路决策点。

通过对华东空管局上海情报中心的2020 年9 月21 日、10 月18 日和10 月20 日的数据进行处理和计算，对邳县附近的A470 和A593 两条航路的航空器等价前后间隔进行计算，航空器发生大于600 m 的高度改变或折线机动则视为拒绝，若航空器始终保持平飞且航向基本不变则认定为接受，最终得到拒绝间隔的范围：14.837 98～108.338 80 km，接受间隔的范围：49.942 70～122.648 60 km。

将所有间隔混合在一起进行从大到小排序后（间隔性质标记也要随排序而改变位置），拒绝间隔（Fr）、接受间隔（Fa）的累积概率计算如下

式中：nr为该拒绝间隔是第nr个拒绝间隔；nr，max为拒绝间隔的总数；na为该接受间隔是第na个接受间隔；na，max为接受间隔的总数。临界间隔的累积概率由式（5）计算。最终得到拒绝间隔、接受间隔和临界间隔概率累积情况。

由式（5）计算得到临界间隔的累积概率后，由Ptc（i）=Ftc（i）-Ftc（i-1）得出每个临界间隔的概率，临界间隔的估计值由E（ttc）=×t（i）计算，其中t 为时间变量，结果为80.473 5 km，小于临界间隔的接受间隔情况为7 个，大于临界间隔的拒绝间隔情况为24 个，因此采用临界间隔可以降低管制员工作负荷。

由于所计算得到的临界间隔为等价前后间隔的临界间隔，不便于直接使用，需要基于上述计算获得的决策点，将该临界间隔转化为实际间隔的临界间隔。

当A470 航路为主要航路时如图11 所示。

图11 A470 航路为主航路的间隔情况Fig.11 Separation circumstance of main course taken by A470

经计算可获知，A470 航路决策点A 距离航路交叉点O 距离为145.299 6 km，A′为决策点A 在A593航路上的投影，AA′距离根据夹角的正弦可得47.304 9 km，A′B 与A′C 为等价前后间隔的临界间隔，CB 为次要航路上的拒绝区间，当主航路上的航空器位于决策点A时，如果次要航路的航空器处于拒绝区间内，管制员应下达避让指令，通过直角三角形性质可以得出，处于临界状态时，两航空器的实际间隔为（AB 或AC 的长度）：93.347 4 km，即在决策点A 处，若两航空器实际间隔小于93.347 4 km，则应该下达避让指令。

当A593 航路为主要航路时如图12 所示。

图12 A593 航路为主航路的间隔情况Fig.12 Separation circumstance of main course taken by A593

与上述过程相同，此时A 为A593 航路的决策点，CB 为次要航路拒绝区间，处于临界状态时，两航空器实际间隔为（AB 或AC 的长度）：91.362 9 km，即处在决策点A 处，若两航空器实际间隔小于91.362 9 km，则应下达避让指令。

4 结语

在对华东空管局上海情报中心实际运行数据进行处理的基础上，通过文献[9-10]的方法计算航空器避让的临界间隔。经过研究分析，使用“临界间隔”可以减少很多不必要的调配，有利于减少管制员和飞行员的工作负荷。

由于本文所采用的数据是以时间、经纬度、高度、航向、速度等元素构成，不包含气象信息和陆空通话的语音信息，因此存在某些较大的“拒绝间隔”并不是由于航空器间隔控制需要而进行的航空器飞行状态调整（不同高度层的气象因素以及飞行员节油需要等因素），所以计算结果会偏大。下一步的研究可以通过陆空通话信息，筛除非间隔控制需要的调配情况，以获得更加准确的结果。