基于模糊层次分析法的无人机运输效能评估

袁子怡，曾 勇

（武警后勤学院，天津 300309）

0 引言

随着现代科技水平的提高，无人机在运输方面具有速度快、适应性强、定位准、人力少、调整灵活等特点，特别是在蜂群式补给、伤病员后送、运输编队防护[1]等方面应用广泛，使得世界各国争相快速发展无人机技术。因此，研究无人机运输效能对整个物流体系具有重要作用。

1 无人机运输效能评估指标体系

1.1 评估思路和步骤

效能评估常用的方法有德尔菲法、层次分析法（AHP）、模糊综合评判法、灰色白化权函数法、主成分分析法（PCA）、正负理想法、ADC 法等[2]，其中德尔菲法、层次分析法主观性较强，过于依赖专家的意见，而主成分分析法和正负理想法使用范围较小，ADC法计算量大且复杂。本文综合各种方法的优缺点，将模糊评价法与层次分析法相结合，解决了专家意见的模糊性和主观性较强的缺点。评估思路：首先，根据专家经验以及相关资料，利用层次分析法构建三级评价指标体系；其次，利用模糊评价法中的三角模糊函数，将其中的定性评价转化为定量评价，从而解决难以量化且模糊的问题，降低主观性带来的影响，从而确定各指标的权重，并对其进行去模糊化和标准化处理；最后，请专家对四款多旋翼无人机的各项指标进行打分，输出综合评估得分，并根据此分数进行比较分析。无人机保障效能评估主要包括构建效能评价指标体系、确定指标权重、专家打分以及输出综合评估结果等4个步骤，如图1所示。

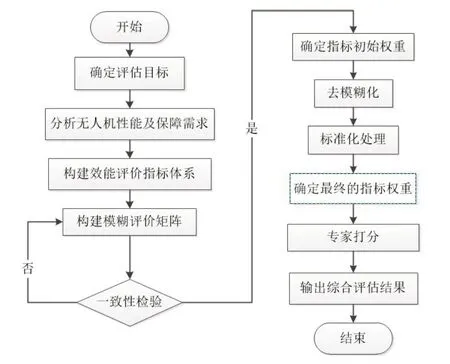
图1 无人机保障效能评估流程图

1.2 无人机运输效能评价指标

根据运输任务需求以及多方面影响因素，结合无人机保障的自身特点，从机体性能、导航能力、保障能力、生存能力、环境适应能力、任务执行能力六个方面[3]构建评价指标体系。其中，考虑到无人机本身的起降能力、飞行速度、续航时间、使用寿命、最大航程因型号、厂家的不同会有所差别，在一定程度上会对其他能力产生影响，进而影响运输效率，因此，将其作为机体性能的二级指标。导航能力是无人机所需具备的最基本的能力，是完成所有任务的前提和基础，包括目标定位、自主导航、自动规划等能力，目标定位的精确性、导航性能的准确性及航线规划的合理性，均有利于提高物资运输效率。保障能力主要考虑无人机的载重能力、载物容积以及装卸能力等。同理，可得到其他一级指标的二级指标，最终得到的无人机运输效能评价指标体系如图2所示。该指标体系共分为3层，按照从上往下、从左往右的顺序对每个指标进行编号。

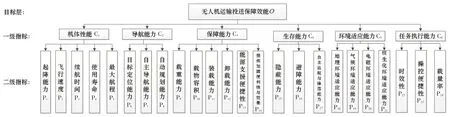
图2 无人机保障效能评价指标体系

1.3 计算运输效能指标权重

无人机保障效能的指标体系包含定性指标和定量指标，由于很难用确定的值来表示定性指标的重要性程度，且模糊性较强，对专家的意见依赖性较强。本文将三角模糊理论与层次分析法相结合，即三角模糊层次分析法[4]，邀请专家对同一层次的指标相对于上层指标的重要性程度进行评估，以三角模糊数的形式来表示，经过一系列步骤确定最终的指标权重。具体计算方法如下：

（1）构建模糊评价矩阵。设指标体系中第T层的第K个指标为XTK，以XTK为参考指标，与XTK相关联的第T+1 层的n个指标可表示为XT+1,1，XT+1,2，XT+1,3，…XT+1,n。邀请3 位相关专家，对T+1 层的任意两个指标进行重要性程度比较，并采用萨迪标度法进行标度。

邀请3位专家根据重要性标度对各指标给出相应的重要性评语，并用三角模糊数来表示专家评语的重要性程度，构建无人机运输效能评价指标体系各个层次的评价矩阵，见表1。

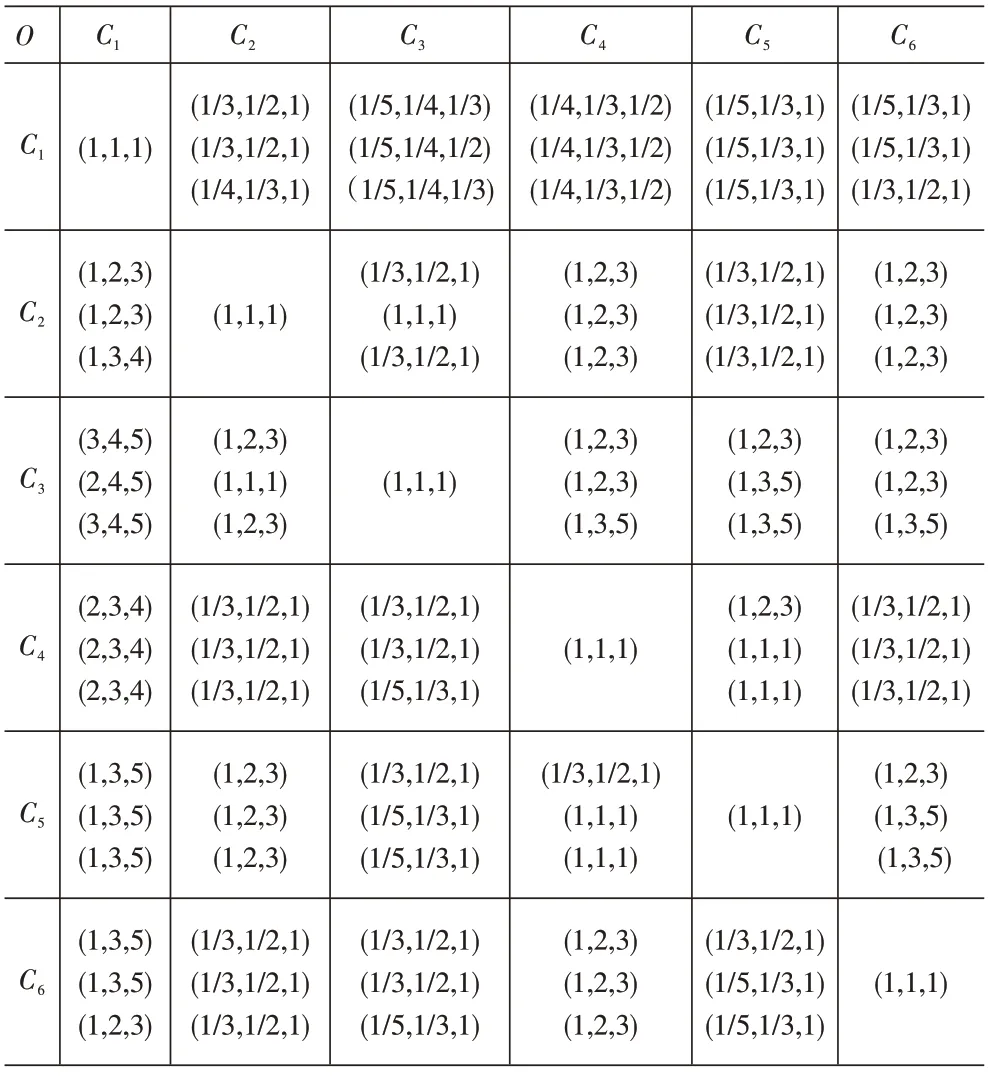
表1 指标{C1,C2,C3,C4,C5,C6} 相对于上一层指标O的评价矩阵

（2）一致性检验。模糊评价矩阵是根据专家经验所得，可能会因为主观因素导致矩阵存在不一致的结论，即可能出现A＞B,B＞C,C＞A 的情况。在模糊评价矩阵中，由于lij和uij的值都在mij附近，且mij是模糊评价矩阵中最重要的值，它的隶属度最大，所以只需检验MTK'=的一致性即可。

①计算模糊评价矩阵的最大特征根λmax。

②计算每个最大特征根的一致性指标CI：

③计算矩阵的检验系数CR：

④判断一致性检验是否通过。若计算所CR<0.1，表示满足一致性条件，若CR>0.1，就需要对矩阵进行调整，直至满足一致性条件为止。

通过计算发现O、C1、C2、C3、C4、C5、C6的一致性检验系数CR均小于0.1，由此判断矩阵满足一致性条件，通过检验。

（3）计算各指标初始权重。首先对模糊评价矩阵进行模糊数整合，然后确定各指标相对于上一层指标的初始权重，公式如下：

①模糊数整合,结果见表2。

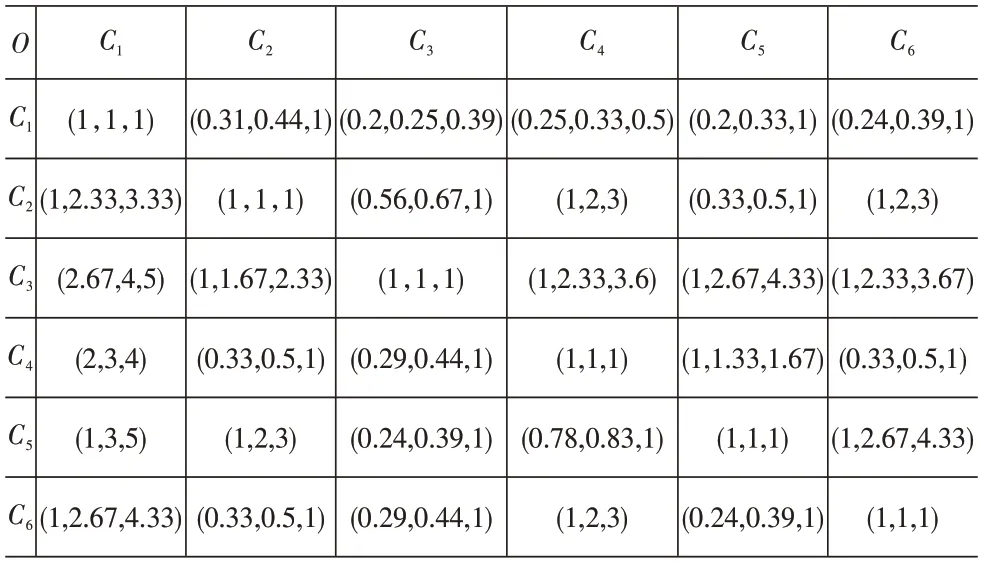
表2 指标{C1,C2,C3,C4,C5,C6} 相对于指标O 的模糊数整合

②确定初始权重，见表3。

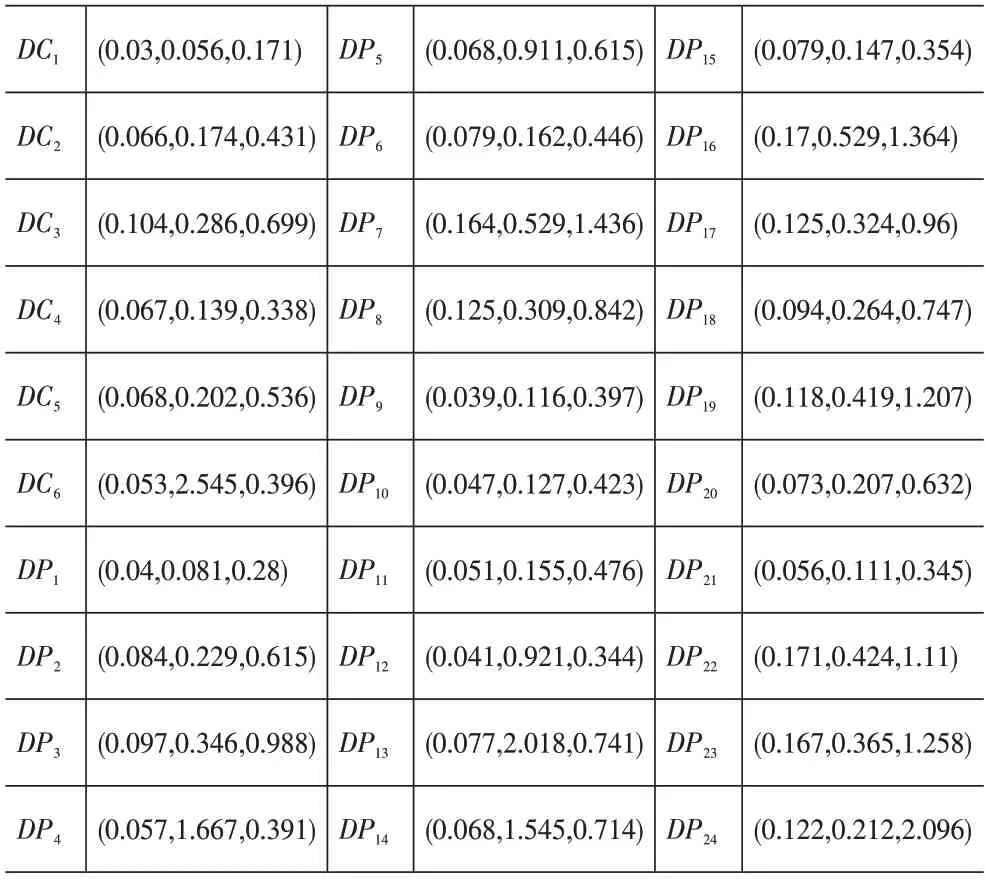
表3 各指标相对于上一层指标的初始权重表

根据指标体系中的层次关系，求出各级指标相对于目标层O的权重，即绝对权重，如下：

2 四款多旋翼无人机保障效能比较评估

2.1 确定评价因素及评价集

本文评估对象主要为某科技公司生产的A、B、C、D四款多旋翼无人机。指标体系中的各指标作为模糊综合评价的因素集，针对本文问题，对各指标设定评价集V：{很好，好，一般，差，很差}，对应的评分集为Z={1，0.8，0.6，0.4，0.2}。

2.2 构建无人机模糊关系矩阵

无人机精确保障评价指标体系包括6 个一级指标，每个一级指标均包括数个二级指标，因此需要构建6个模糊关系矩阵R。本文假设专家已根据图2的评价指标体系对四款无人机进行了评分，得到了模糊关系矩阵，本文以A款无人机为例，其余三款无人机计算方法类似。

其中矩阵中数字表示专家对各指标的评价在评分集中所占比重，例如，(0.2,0.4,0.3,0.1,0)表示有20%的专家认为P1指标很好，40%的专家认为好，30%的专家认为一般，10%的专家认为差，0%的专家认为很差，以此类推。

2.3 计算模糊综合评判得分

由权重向量Ai和模糊关系矩阵Ri，计算评价向量Bi=Ai*Ri(i=1,2,...,6），进而得到目标层的模糊关系矩阵R0。

A款多旋翼无人机的目标层模糊关系矩阵R0为：

进而求得评价向量：

利用Bi*评分集ZT分别求得A、B、C、D 四款多旋翼无人机的最终综合得分及各一级指标的具体得分，见表4。

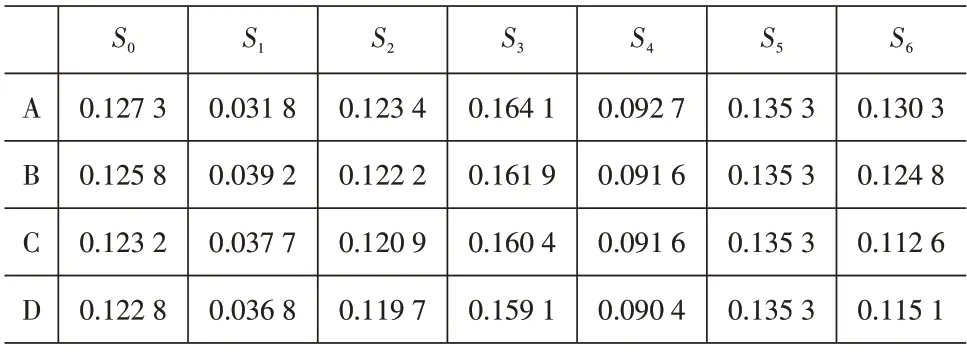
表4 四款多旋翼无人机得分

由表4 可知：综合效能A＞B＞C＞D，机体性能B＞C＞D＞A，导航能力A＞B＞C＞D，保障能力A＞B＞C＞D，生存能力A＞B=C＞D，环境适应能力A=B=C=D，任务执行能力A＞B＞D＞C。综合而言，A型无人机更适合物资运输任务。

3 结语

无人机是未来无人智能化物流的主要手段，无人机运输效能在一定程度上决定着物流效率。本文针对无人机运输的特点与影响因素，在建立无人机运输效能评价指标体系的基础上，应用模糊层次分析法确定各层级指标权重，最终用模糊综合评价法对四款无人机的运输效能进行评分，为今后研究无人机运输效能提供参考依据。