基于正交试验的采空区下单轨吊巷道支护参数优化研究

章 曼，刘钦节,2，付 强,2，杨卿干，陈 强

（1.安徽理工大学矿业工程学院，安徽 淮南 232001；2.安徽省关闭/废弃矿井资源开发利用工程研究中心，安徽 淮南 232001）

0 引言

矿井运输是煤炭产业链中的重要环节，运输内容包括煤炭、矸石、人员、设备与材料等[1-3]。单轨吊作为一种多功能、高效率、多用途的煤矿井下运输设备，近年来得到迅速推广应用[4-5]。但由于隐蔽性强、影响因素多而难以准确确定等原因，部分企业易忽视采空区及支护强度不足对巷道围岩控制的影响，矿井运输重大事故仍时有发生。因此，如何保证巷道支护的有效性，成为井下工作面实施单轨吊运输必须研究解决的重大课题。

目前，已有众多专家针对巷道围岩支护展开了研究。在支护参数优化方面，王岗风等[6]、马胜杰等[7]、胡建华等[8]、康明超等[9]利用正交试验法选取不同参数组合进行数值模拟对比，对巷道支护参数进行了优化。在协同支护方面，刘刚等[10]基于传统支护理论与实际支护条件，提出了巷道协同支护设计。王君[11]、秦志宏等[12]、陈才贤等[13]、李百宜等[14]、李志臣等[15]、赵呈星等[16]采用数值模拟方法，基于协同支护作用，提出了众多联合支护方案。在单轨吊巷道支护方面，尚伟栋[17]通过分析在单轨吊作用下3210 回风巷道顶板的稳定性，提出了孤岛工作面回风巷采用悬吊锚杆和悬吊锚索相结合的支护方式；谢生荣等[18]提出了将巷道顶板视为深梁进行稳定性分析，并采用密集布置的高预应力锚索和强力锚杆支护系统构建了顶板锚固复合深梁承载结构。

综合上述研究发现，目前对单轨吊荷载作用下的巷道协同支护研究较少。为此，在潘二矿18124 工作面单轨吊轨道梁受力分析的基础上，设计了三水平三因素的支护参数正交试验以获得不同参数下的支护效果和变形规律，并采用极差分析得出影响巷道变形的敏感性因素，确定合理的支护形式和参数，为采空区下单轨吊运输巷道支护提供重要参考。

1 工作面概况

潘二矿18124 工作面上覆为18125 工作面采空区。根据掘进及地质钻孔资料，工作面4-1 煤层直接顶板为砂质泥岩，局部含有细砂成分，性脆、平坦，滑面发育，岩性破碎，平均厚度为5 m；砂质泥岩之上为4-2 煤层，平均厚度为2.6 m，内部发育一层平均0.9 m 的泥岩夹矸，4-1 煤层老顶为砂质泥岩，岩性破碎，平均厚度为3.3 m。直接底为泥岩，平均厚度为2.0 m，深灰色，块状，泥质成分，可见植化碎屑，岩性破碎，局部发育煤线。工作面单轨吊运行线路图如图1 所示。

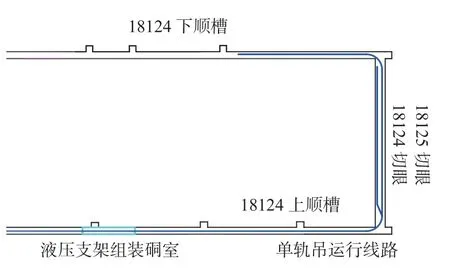
图1 18124 工作面单轨吊运行线路图Fig.1 Running circuit diagram of monorail crane in 18124 working face

2 单轨吊承载液压支架受力分析

工作面主要使用一部DZK3500（2+2）柴油单轨吊，用于在上顺槽井下组装硐室内组装完成支架ZZ7200/22/45 d（重量27 t）的整架吊装与运输，柴油单轨吊运输液压支架系统示意图如图2 所示。单轨吊轨道梁受力系统可按照多跨简支梁进行计算[19]。水平巷道运输时，整个轨道并不是均匀受力，由于轨道中受力最大的点在起吊梁的承载车上，因此对轨道的受力分析，可只考虑最大受力点的起吊梁段轨道的受力分析。

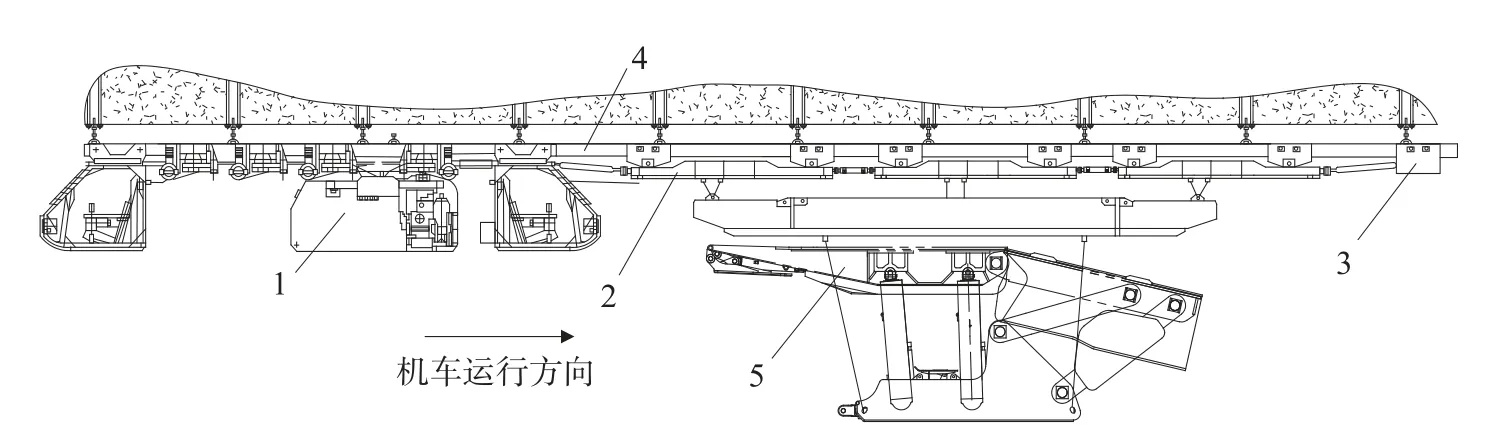
图2 柴油单轨吊运输液压支架系统示意图Fig.2 Schematic diagram of hydraulic support system for diesel monorail crane transportation

轨道承载27 t 液压支架，16 t 起吊梁自重1.49 t，共3 组起吊梁，12 个承载小车平均受力，计算见式（1）。

单个承载小车负载为2.62 t，将轨道简化为两端简支的梁进行计算，轨道受力分析如图3 所示，B吊挂点负载表达式见式（2）。

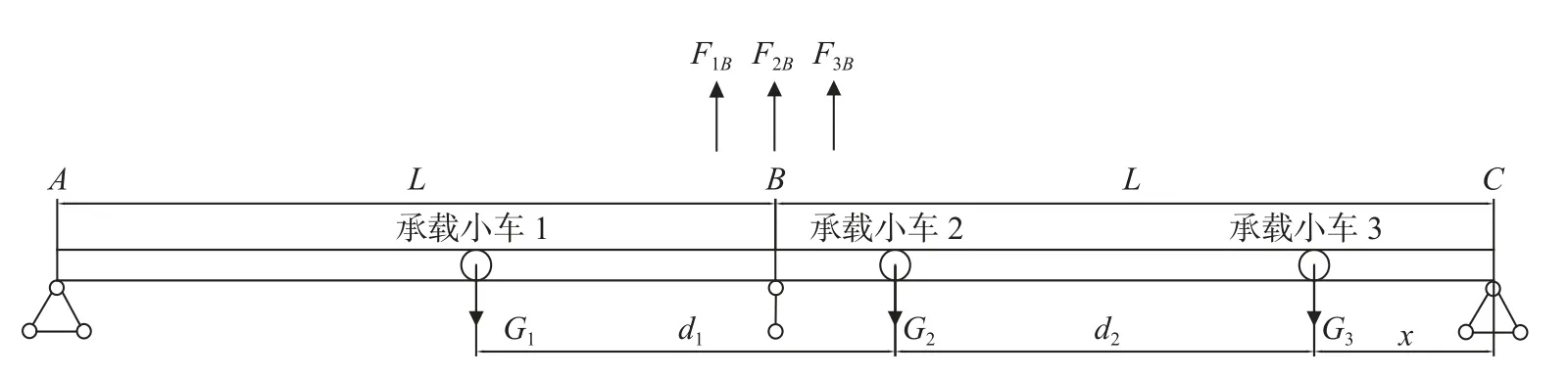
图3 轨道受力分析图Fig.3 Diagram of track stress analysis

式中：F1B、F2B、F3B为承载小车1、承载小车2、承载小车3 对B点的作用力，kN；G为单个小车载荷大小，kg；L为轨道长度，m；d1、d2为承载小车间距离，m；x为承载小车2 距离C点的距离，m；q为轨道单位长度质量，kg/m。

由式（2）可知，当L-d2-x=0 时，FB可取最大值，将G=2 622.50 kg、L=2.40 m、d=2.01 m、q=34.50 kg/m，带入式（2）计算可得FB=3 513.90 kg。

根据上述计算可知，潘二矿18124 工作面单轨吊在整架运输液压支架时最大的悬挂点荷载约为34.43 kN，取3 倍安全系数，则每根锚杆的承受力平均为34.43 kN，每根锚索的承受力平均为103.28 kN。

3 研究方法

3.1 正交试验设计

为保证分析快速高效，采用正交试验法设计试验[20]。影响锚杆索支护强度的因素众多，主要有锚杆间排距、锚杆直径、锚杆长度、锚索间排距、锚索直径、锚索长度等。由于锚杆锚索之间存在协同支护作用，因此选用三水平三因素正交实验法分别对锚杆锚索设计不同参数组合，快速筛选主要影响因素。参数水平见表1。

3.2 极差分析法

极差分析法主要通过R值大小判断因素间优势或因素间具体水平的优劣，当因素间出现相互作用互为矛盾时，优先考虑显著因素，R值越大，表明该影响因素水平变动时对计算结果影响越大，即该影响因素越具有显著性。因此，采用极差分析法对影响锚杆锚索支护强度的各参数进行敏感性分析。

3.3 间排距协同支护方案

为探究锚杆间排距、锚索间排距对巷道变形的影响，选取最优锚杆长度、锚索长度、锚杆直径、锚索直径参数保持不变，将不同的锚杆间排距、锚索间排距进行组合，模拟方案见表2。

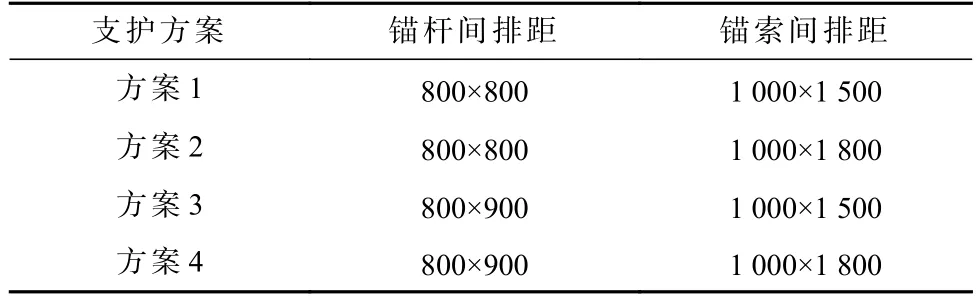
表2 锚杆间排距、锚索间排距协同支护模拟方案Table 2 Simulation scheme of row spacing cooperative support between anchor bolts and cables 单位：mm

3.4 数值模型建立

采用高阶曲面三维建模软件Rhinoceros 进行随机网格划分，并结合FLAC3D数值模拟软件建立单轨吊作用下巷道围岩模型。锚杆给顶板施加22.3 kN垂直向下的载荷，锚索给顶板施加67 kN 垂直向下的载荷，如图4 所示，尺寸为X×Y×Z=70 m×30 m×60 m。本次设计选取断面尺寸为：a=5.4 m，H=3.9 m，ϕ=33°，其中，a为巷道宽度，H为巷高，ϕ为岩体的折算摩擦角。

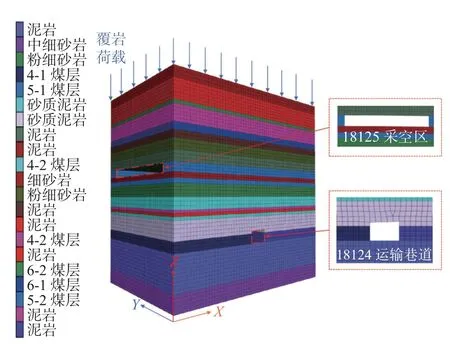
图4 数值模型图Fig.4 Diagram of numerical model

4 模拟结果分析

4.1 正交试验结果及敏感因素分析

试验选用顶底板及两帮位移量作为正交试验考察指标。根据上述因素水平表共设计出18 组正交试验并采用极差分析法对锚杆锚索参数进行分析，结果如图5 和图6 所示。由图5 和图6 可知，当锚杆锚索间排距越大，长度越短，直径越小时，巷道顶底板及两帮变形量越大。此外，锚杆间排距800 mm×800 mm、锚杆长度2.5 m、锚杆直径24 mm 时，巷道位移值为最小。

图5 锚杆锚索参数正交试验结果Fig.5 Orthogonal test results of parameters of anchor bolts and cables

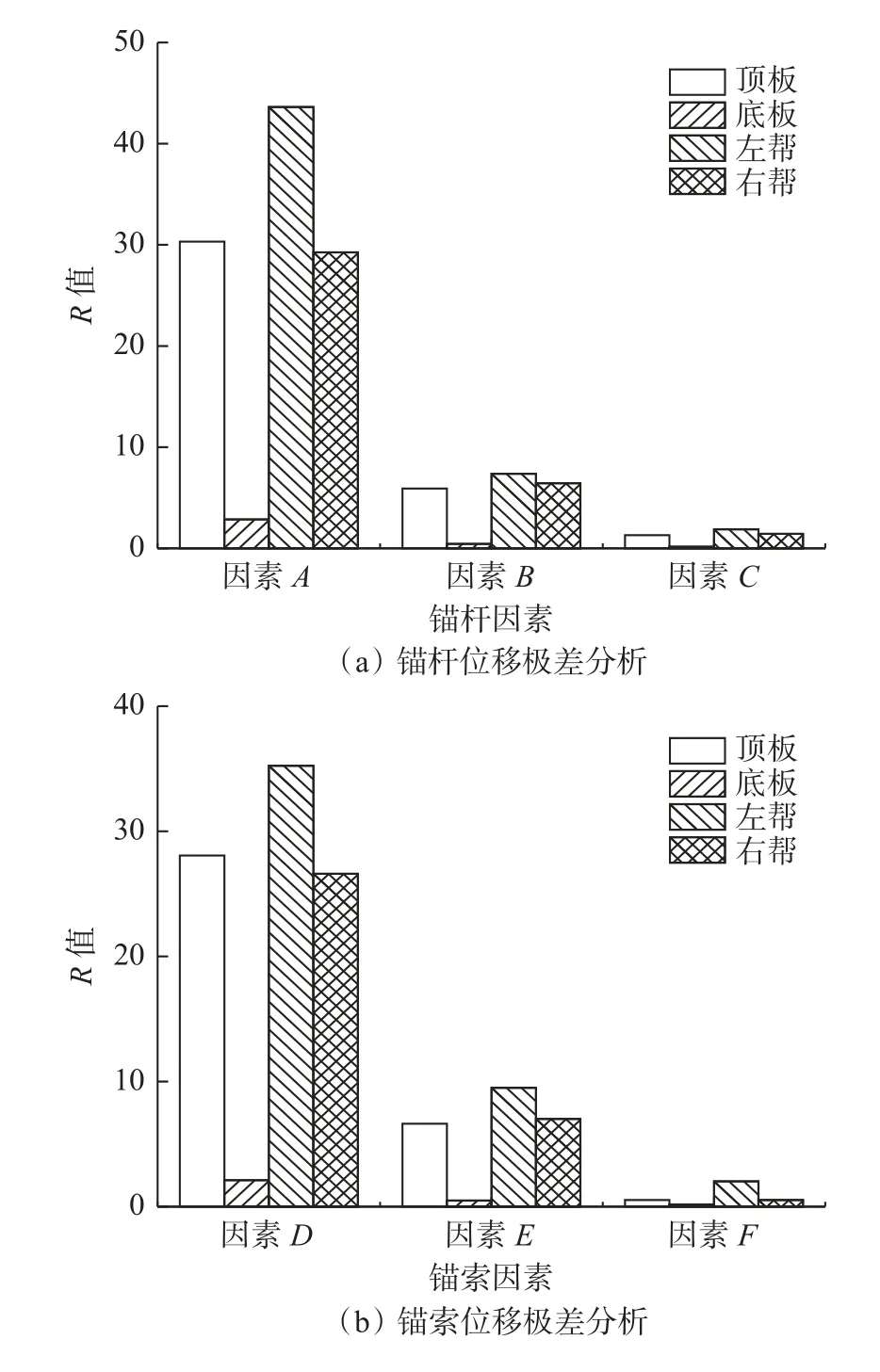
图6 锚杆锚索位移极差分析Fig.6 Analysis of displacement range of anchor bolts and cables

依据极差分析结果可知，控制其他因素不变时，巷道变形影响因素敏感性排序依次为：锚杆间排距A＞锚杆长度B＞锚杆直径C（锚索间排距D＞锚索长度E＞锚索直径F），即锚杆间排距、锚索间排距对巷道变形影响程度最大，锚杆长度、锚索长度次之，锚杆直径、锚索直径最小。

4.2 锚杆锚索间排距协同支护作用下围岩稳定性分析

考虑锚杆锚索协同支护作用，并进一步优化巷道支护参数，在不考虑地应力且保持其他因素不变的情况下，对间排距匹配的四组支护方案进行数值模拟，如图7～图9 所示。

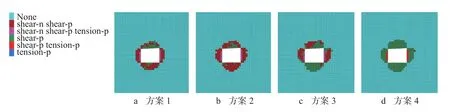
图7 塑性区分布图Fig.7 Distribution diagram of plastic zone

4.2.1 塑性区分布特征

各支护方案下巷道附近围岩塑性区体积变化情况如图7 所示。由于巷道右帮受到工作面超前支承压力影响较大，巷道右帮塑性区大于左帮。根据图7各方案模拟计算得到的塑性区值大小分析，方案1计算得到的塑性区体积最小，为855.00 m3，其余方案塑性区体积分别为967.50 m3、1 068.75 m3、1 121.25 m3，均满足支护要求。

4.2.2 位移变化特征

1）垂直位移分析。各支护方案下巷道附近围岩垂直位移变化情况如图8 所示。巷道顶板以整体下沉为主，底板以中间底鼓为主。各方案顶板位移变形量分别为134.58 mm、142.44 mm、147.87 mm、156.34 mm，底板位移变形量分别为28.20 mm、28.47 mm、29.08 mm、29.84 mm。分析可知，巷道顶板与底板的位移变形量随锚杆锚索间排距的减小而减小。当锚杆间排距小于800 mm×900 mm，锚索间排距小于1 000 mm×1 800 mm 时，巷道顶底板位移变形量逐步减小并趋于稳定。

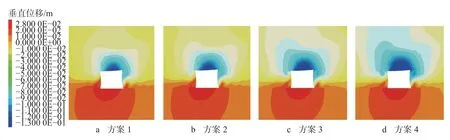
图8 垂直位移云图Fig.8 Cloud diagram of vertical displacement

2）水平位移分析。各支护方案下巷道附近围岩水平位移变化情况如图9 所示。受直角梯形断面影响，高帮位移量大于低帮位移量。各方案高帮位移变形量分别为221.95 mm、225.60 mm、228.71 mm、237.92 mm，低帮位移变形量分别为186.65 mm、194.03 mm、205.38 mm、216.92 mm。分析可知，巷道两帮的位移变形量随着锚杆锚索间排距的减小而减小，当锚杆间排距小于800 mm×900 mm，锚索间排距小于1 000 mm×1 800 mm 时，两帮位移变形量逐步减小并趋于稳定。

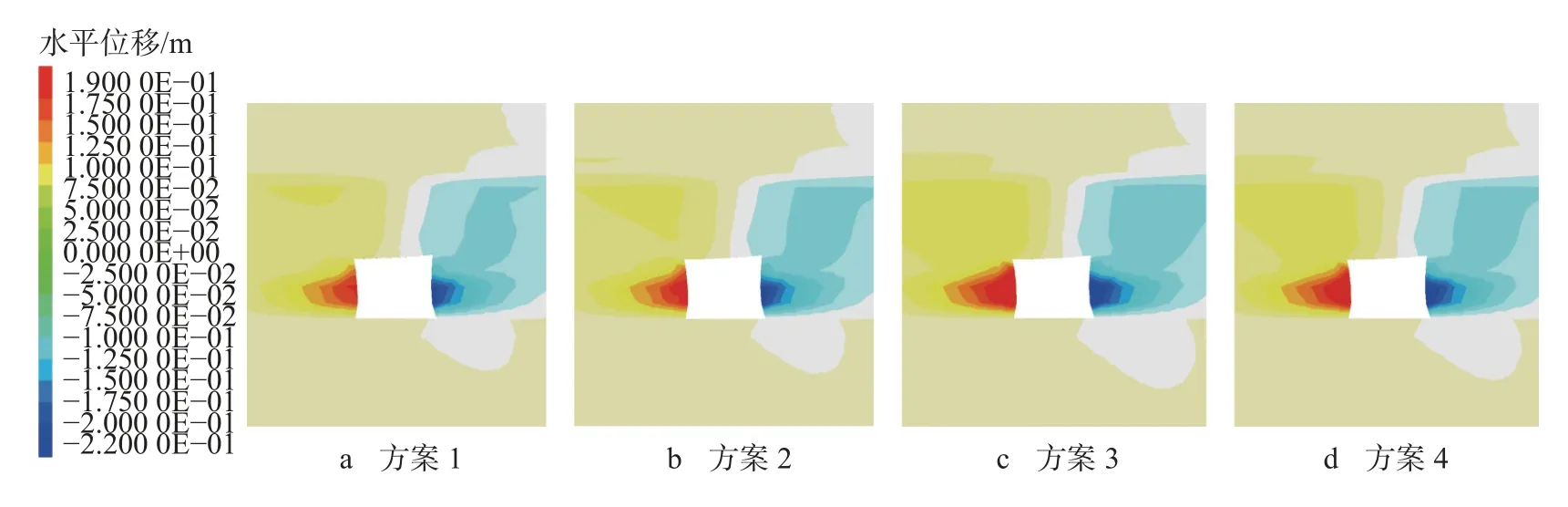
图9 水平位移云图Fig.9 Cloud diagram of horizontal displacement

4.3 支护方案选取

协同支护方案塑性区、位移及用钢量对比结果如图10 所示。对比各支护方案塑性区体积大小，相较于方案1，方案2 的塑性区体积增加了13.16%，方案3 增加了25.00%，方案4 增加了31.14%，即以塑性区体积为衡量指标时，方案1 确定的巷道支护参数较优。对比各方案支护效果可知，相较于方案1，方案2 的围岩变形量（顶板、底板、左帮、右帮）分别增加了5.84%、0.96%、3.95%、1.64%，方案3 增加了9.88%、3.12%、10.03%、3.05%，方案4 增加了16.17%、5.82%、16.22%、7.20%，即以支护效果为衡量指标时，方案1 确定的巷道支护参数为较优。对比各方案经济合理性可知，相较于方案1，方案2 的用钢量减少了6.34%，方案3 的用钢量减少了6.89%，方案4 的用钢量减少了13.23%，即以经济合理性为衡量指标时，方案4 确定的巷道支护参数较优。

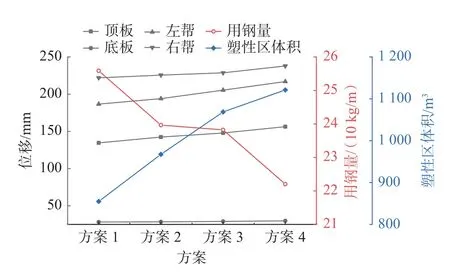
图10 协同支护方案塑性区、位移及用钢量对比Fig.10 Comparison of plastic zone,displacement and steel consumption of collaborative support scheme

上述四种支护方案均满足巷道安全运输要求，但对围岩的控制程度有所差异。方案4 的围岩变形量虽略大于其他方案，但能够在不影响支护效果的情况下有效降低支护成本。综合考虑支护效果与经济成本，确定方案4 为优选方案，具体参数为：锚杆间排距800 mm×900 mm，锚杆长度2.5 m，锚杆直径22 mm，锚索间排距1 000 mm×1 800 mm，锚索长度9.3 m，锚索直径22 mm。

5 结论

1）以巷道顶底板及两帮位移量为控制目标，依据正交试验法和极差分析法得到了影响巷道变形的敏感性因素排序：锚杆间排距A＞锚杆长度B＞锚杆直径C（锚索间排距D＞锚索长度E＞锚索直径F）。

2）分析试验结果可知，巷道位移变形量减小趋势为：当锚杆间排距小于800 mm×900 mm，锚索间排距小于1 000 mm×1 800 mm 时，巷道围岩变形趋于稳定。

3）综合考虑支护效果与经济成本，选取支护参数为：锚杆间排距800 mm×900 mm，锚杆长度2.5 m，锚杆直径22 mm，锚索间排距1 000 mm×1 800 mm，锚索长度9.3 m，锚索直径22 mm。模拟结果表明，巷道围岩得到了有效控制，可满足单轨吊运输巷道运输物料的安全需求，降低支护经济成本。