融合多测点数据相关性的大坝监测历史数据填补

刘 鹤 鹏,李 登 华,丁 勇

(1.南京理工大学 理学院,江苏 南京 210094; 2.南京水利科学研究院,江苏 南京 210029; 3.水利部水库大坝安全重点实验室,江苏 南京 210029)

0 引 言

大坝安全监测数据是大坝安全运行和正常维护工作的重要指标,是水利“四预”工作中的重要依据[1]。而在实际工程中,数据采集、传输、存储等环节受各类因素影响,往往会使测量数据遭受不同程度的缺失,将影响大坝安全性的准确评估[2]。因此,监测数据的完整性和精准性备受关注[3]。

目前,处理缺失值的传统手段大都是基于统计学的理论建立的,如中位数填补法[4]、均值填补法[5]、众数填补法[6]、线性插值填补法[7]以及多重插值填补法[8]等。随着近年来对机器学习和其他新型学科研究的不断深入,一些学者提出了全新的缺失值填补思想。李双平等[9]比较了常用的数学插值方法,选择了具有平滑插值曲线的三次Hermite分段插值,充分利用现有数据信息进行数据序列的均质化处理。文雯[10]在原有KNN的基础上引入了灰色理论,并提出了一种新的加权灰色KNN方法对缺失值进行填补,通过融入加权灰色理论对传统KNN算法进行一定程度的改进。Ramzan等[11]提出通过挖掘测点时间序列的自回归性来填补缺失值。王娟等[12]针对含有缺失值的监测数据,使用核独立分量分析法将提取的独立分量作为预测模型的输入项进而预测缺失值。但这些研究针对大坝安全监测数据集而言,仍存在一些问题,如对于数据相似性的依赖度较强、对高缺失率数据集填补精度较低、应对大坝安全监测数据集中不同缺失值类型的鲁棒性较差等。

有鉴于此,本文通过分析多座现役大坝的实测资料,对大坝安全监测数据集中存在的缺失值类型进行归纳总结,并针对不同类型的缺失值提出了一种基于各测点时间尺度相关性的缺失值填补新算法,旨在考虑时间序列间相关性的同时,引入迭代技术实时更新时间序列间的相关性,弥补传统算法处理缺失值精度低的不足,并实现多测点缺失值的自动化填补。

1 监测数据集中缺失值的分布类型

通过文献调研,并基于多座大中型水库的多年实测资料,研究发现监测数据的主要缺失类型有以下几种。

针对单一测点的主要缺失值类型:

(1) 不同的缺失率[13],体现在相同时间段内缺失值数量占该时间段全部数据量的比值不同。不同缺失率的时程曲线见图1。

图1 不同缺失率下时间序列的时程曲线Fig.1 Time history curves of time series under different missing rates

(2) 不同的离散程度[14],主要有3种形式:① 离散型缺失;② 连续型缺失;③ 混合型缺失。

离散型缺失:在数据分布上呈现为缺失值在时间序列内分散分布、不连续。筛选并剔除数据集中的异常值是造成此类型缺失值的主要原因,此类型缺失数据集的历史过程线见图2(a)。

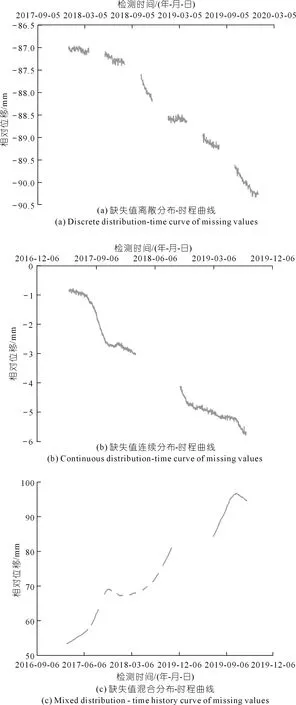
图2 不同缺失值离散度下时间序列的时程曲线Fig.2 Time history curves of time series under different dispersion degree of missing value

连续型缺失:在数据分布上呈现为密集且连续出现缺失值。数据采集系统故障是造成此类型缺失值的主要原因,此类型缺失数据集的时程曲线见图2(b)。

混合型缺失:在数据分布上呈现为在时间序列内同时存在离散型和连续型分布。此类缺失类型在大坝安全监测数据集中较为普遍,典型时程曲线见图2(c)。

由于目前各项数据挖掘研究均需参考测点的空间分布特征[15-17],故针对多测点的缺失值填补算法也需考虑缺失值在空间尺度的分布情况。在空间尺度中主要的缺失类型有:① 集中型缺失;② 均匀型缺失。

集中型缺失:在数据分布上呈现为缺失值存在于一片区域测点的时间序列中的少数测点内。造成此类型缺失值的主要原因是正常工作的测点群中出现少数测点发生损坏导致数据采集缺失,此类型缺失数据集的时程曲线见图3(a)。

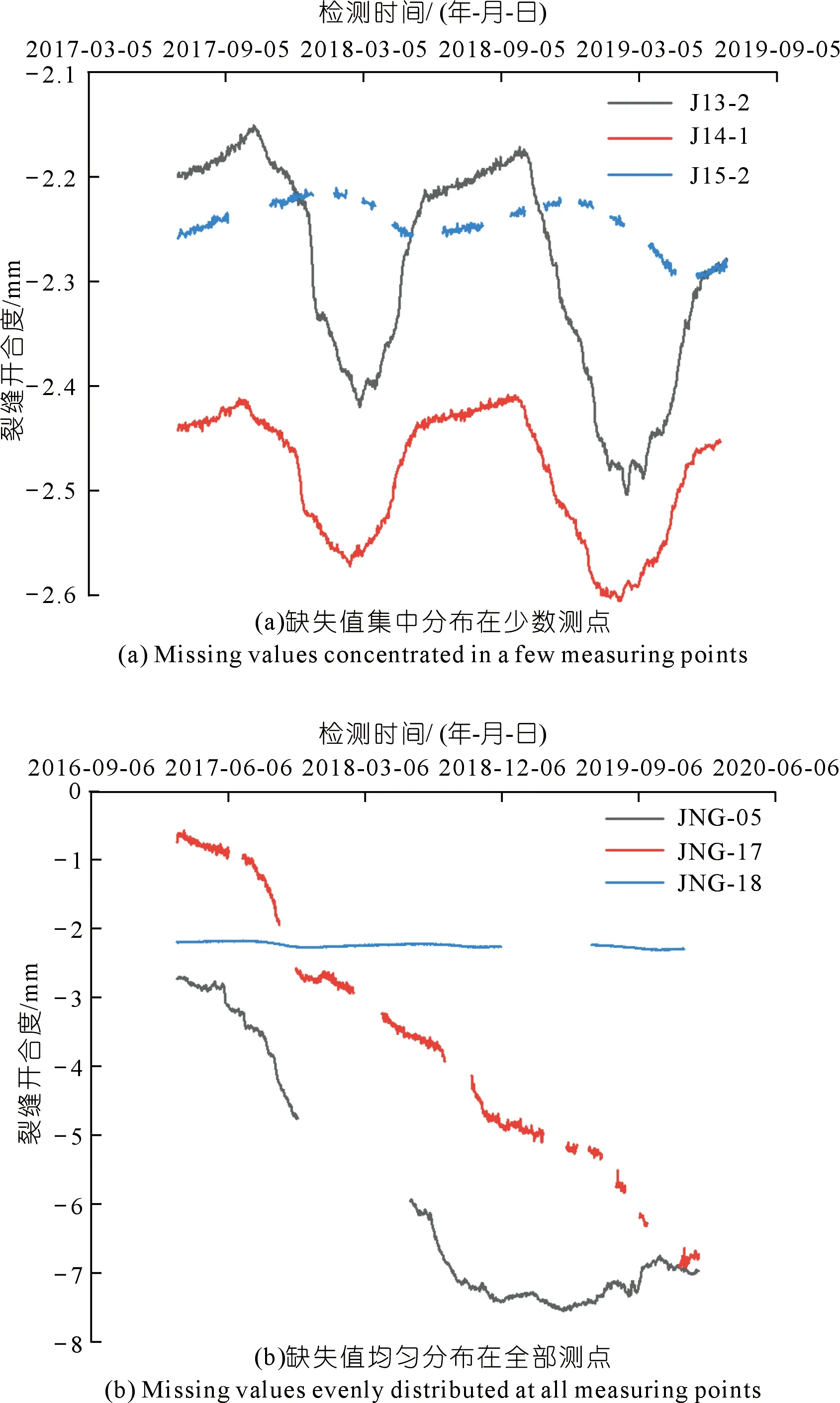
图3 不同缺失值集中度下时间序列的时程曲线Fig.3 Time history curves of time series under different missing value concentration

均匀型缺失:在数据分布上呈现为缺失值均匀存在于一片区域测点的时间序列中。当此区域出现区域性系统问题时,该区域内所有仪器均无法采集数据,进而导致此类型的数据缺失,此类型缺失数据集的时程曲线见图3(b)。

2 融合多测点数据相关性的缺失值填补新算法

传统缺失值填补算法或基于自回归模型,或依据数据相似性,这些算法无法挖掘时间序列内存在的潜在信息,但大坝作为整体,其各个监测量之间存在一定相关性[18],有鉴于此,本文提出基于时间尺度相关性的缺失值填补新算法。

在统计学中常使用相关系数来描述两个变量之间的相关程度,不同类型数据适用的相关系数不同。针对大坝安全监测数据集而言,由于行业中一般假设数据集内各变量符合正态分布[19],故本文选择Pearson相关系数[20]来定量衡量各时间序列之间的相关性,记为r,是一种线性相关系数,用来反映两个变量X和Y的线性相关程度,其具体表达式如下,相关系数介于-1～1之间,绝对值越大表明两变量之间的相关性越强。

基于时间尺度相关性的缺失值填补新算法其核心在于预测模型中作为输入项的时间序列的选取,寻找与目标待填补缺失值所在时间序列存在一定相关关系且符合一定要求的时间序列,并将这些时间序列作为预测算法的输入项,进而预测填补缺失值。在输入项选取上应遵循以下原则:① 作为输入项的时间序列不可与目标缺失值存在同一时段的缺失;② 作为输入项的时间序列需与目标填补时间序列之间满足一定的相关度。

新算法的基本步骤如下:

(1) 标记输入模型中每条时间序列中的缺失值Xi。

(2) 计算各时间序列之间的Pearson相关系数r。

(3) 将包含缺失值Xi的时间序列输入到模型中,筛选3个以上与缺失值Xi所在时间序列r在0.95～1.00区间范围内,且不与该缺失值同一时段缺失的时间序列进行建模,将上述筛选的时间序列中连续部分作为训练集,将缺失部分作为测试集输入预测模型并输出预测值,将预测值作为缺失值的填补值,并将填补后的时间序列重新放回数据集中。如符合上述步骤要求的时间序列数量仅有2个时,则引入至少一个已经填补后的符合上述要求的时间序列来构建输入项。如符合上述步骤要求的影响因子数量仅有一个时,则引入至少2个已经填补后的符合上述步骤要求的时间序列来构建输入项。

(4) 检测数据集中是否存在缺失值,如有缺失值则进行下述步骤,若检测到没有缺失值则直接输出完整的数据集。

(5) 由于数据集中缺失值得到填补,需重新计算各时间序列之间的Pearson相关系数r。

(6) 重复步骤(3)～(5)。

(7) 如缺失值Xi在完成上述填补后仍存在缺失值,则将步骤(3)要求的r区间降低至0.90～0.95,并重复上述填补过程。

(8) 如缺失值Xi在完成上述填补后仍存在缺失值,则将步骤(3)要求的r区间每次以0.05为区间长度进行降低,并重复上述的填补过程,直至所有缺失值得到填补。

整个流程如图4所示。

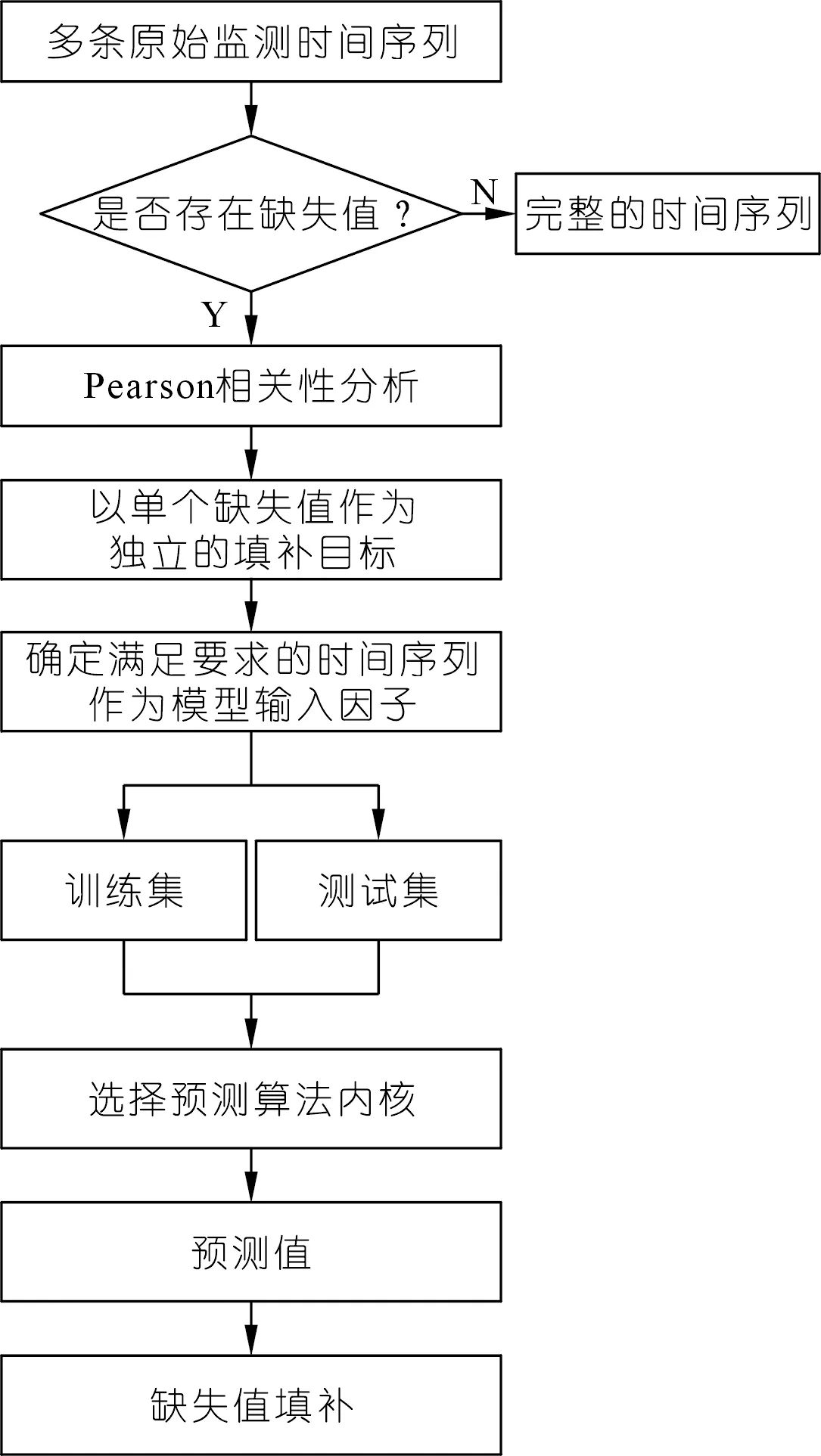
图4 融合多测点数据相关性的缺失值填补新算法流程Fig.4 Flowchart of new missing value filling algorithm based on fusion of multi-point data correlation

3 验证试验

3.1 试验设计

本次试验以新疆开都河流域内察汗乌苏水电站混凝土面板堆石坝的安全监测数据集为依据,进行了两次缺失值填补试验。试验一测试了填补算法对于不同类型缺失值数据集的填补性能,试验二测试了在真实数据集下填补算法对于缺失值的填补效果。在该堆石坝坝左0+154、坝左0+200、坝左0+202此3个监测断面内高程1 579～1 619 m的面板区域中共布设了30个测点[见图5(a)],安装包括面板测缝计、钢筋应力计、渗压计、混凝土应变计等4类监测仪器。监测时间为2017年1月1日至2020年12月31日。这些测点由于在空间上邻近,受到的环境作用以及其他因素的影响相似,故这些测点在时间尺度上存在一定的相关性,各测点时间序列间Pearson相关系数热力图如图5(b)所示。

试验一在原有完整数据集上构建缺失值,通过不同缺失值分布类型来真实地还原原始数据集中缺失值的分布情况。在缺失率层面设置小缺失率(1%)和大缺失率(10%)两种情况;在集中度层面设置为集中在少数测点缺失和均匀在全部测点缺失两种情况;在离散程度层面设置离散型缺失、连续型缺失以及混合型缺失3种情况。综合上述3个层次的组合,共模拟12种包含不同类型缺失值的数据集,具体对应编号如表1所列。

表1 包含不同类型缺失值数据集对应编号Tab.1 Corresponding numbering of data sets containing different types of missing values

试验二为测试各算法在实际工程中对于缺失值的填补效果,选取上述测点群中的R23测点(所测量的物理量为径向位移),对其实测数据中2017年10月27日至12月25日存在的缺失值进行填补测试。

本次试验使用了目前机器学习领域中认可度广且成熟度高的3种机器学习算法:BP神经网络、SVM(support vector machine)、多元线性回归(LR)[21-22],将这3种算法分别作为预测填补算法中的预测模型内核。同时为对比对缺失值填补的性能,选择KNN最近邻填补法和线性插值填补法同时对上述12种包含不同类型缺失值的数据集进行缺失值填补,并对填补结果进行对比分析。

为了对比不同缺失值填补算法对于缺失值的填补精度,本文利用均方根误差[23](RMSE)以及归一化平均绝对百分比误差[24](nMAPE)作为评价填补算法对于缺失值填补精度优劣的指标。

3.2 试验结果分析

本文提出的缺失值填补算法、KNN最近邻填补法以及线性插值填补法针对数据集1,2,3,7,8,9的填补精度结果如表2～3所列。

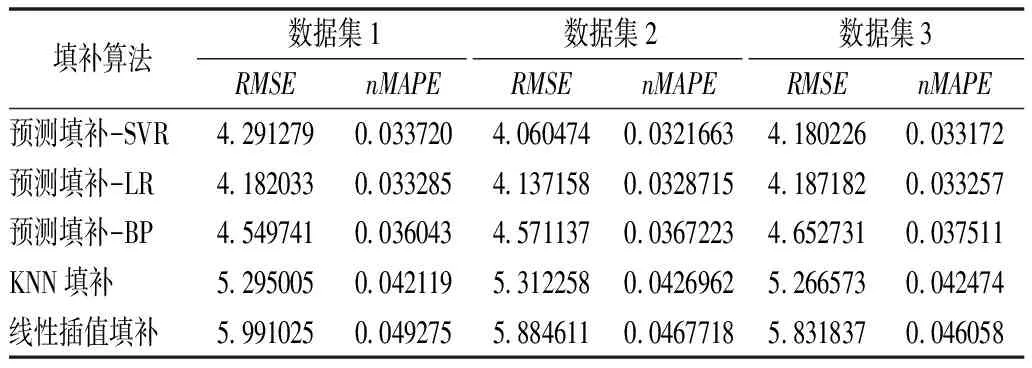
表2 不同填补算法针对数据集1～3的填补精度Tab.2 Filling accuracy of different filling algorithms for data sets 1～3

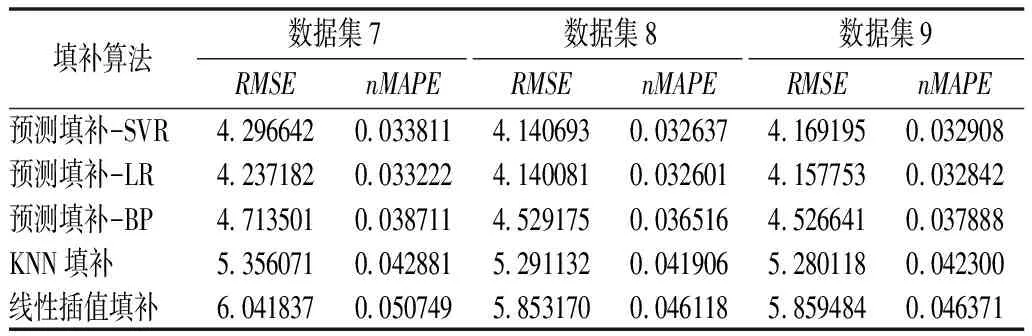
表3 不同填补算法针对数据集7～9的填补精度Tab.3 Filling accuracy of different filling algorithms for data sets 7～9

由表2～3可知,当缺失率、集中度为常量时,各填补算法对于离散型缺失数据集的填补效果均优于连续型和混合型缺失数据集,对于连续型缺失数据集的填补效果最差。当缺失率、离散程度为常量时,各填补算法对于集中缺失型数据集的填补效果均优于均匀缺失型数据集。不同预测模型内核对缺失值的填补效果也有一定影响,其中LR、SVR内核对于不同类型的缺失数据集拟合效果较好,且在应对不同类型缺失数据集时两种模型内核的表现差异不大,BP神经网络内核的拟合效果较差,但也优于其余填补算法。

本文填补算法在各预测模型内核下针对数据集1,2,3,7,8,9的RMSE均值为4.317 934,nMAPE均值为0.034 305;KNN填补法的RMSE均值为5.300 193,nMAPE均值为0.042 396;线性插值填补的RMSE均值为5.910 327,nMAPE均值为0.047 557。相对而言,本文填补算法的各项精度指标的平均值针对小缺失率的情况下的不同类型缺失值数据集均优于其他填补算法,其中RMSE均值相较于KNN填补法的RMSE均值提升了18.53%,相较于线性插值填补法的提高了26.94%;nMAPE均值相较于KNN填补法的提升了19.08%,相较于线性插值填补法的提高了27.86%。

同理,不同填补算法针对数据集4,5,6,10,11,12的填补精度结果如表4～5所列。

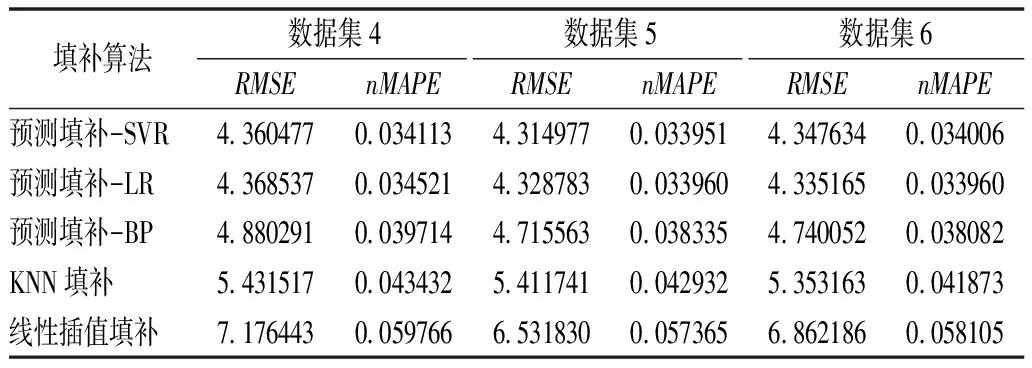
表4 不同填补算法针对数据集4～6的填补精度Tab.4 Filling accuracy of different filling algorithms for data sets 4～6

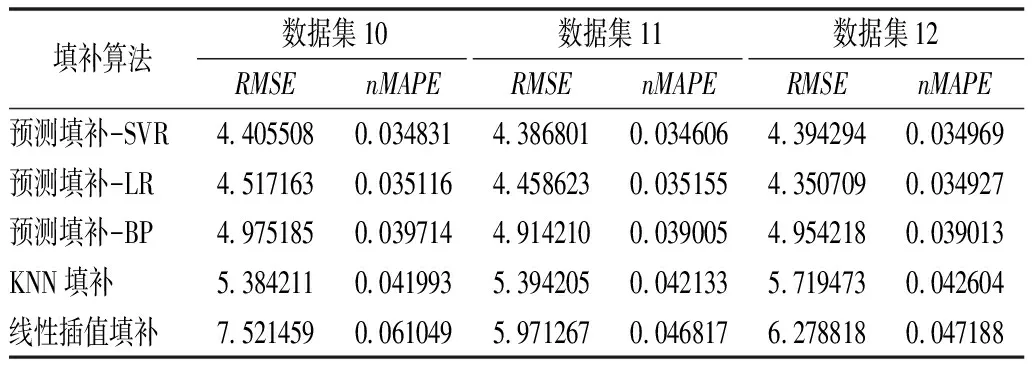
表5 不同填补算法针对数据集10～12的填补精度Tab.5 Filling accuracy of different filling algorithms for data sets 10～12

同时随着缺失率的提升,各填补算法的填补精度虽均有所下降,但本文所提算法的下降率更低,RMSE均值在缺失率为10%的情况下相较于1%时下降了0.223 632,下降率为5.2%,nMAPE均值下降了0.001 694,下降率为4.9%。而KNN填补法的RMSE均值在缺失率为10%的情况下相较于1%时下降了0.132 192,下降率为5.7%,nMAPE均值下降了0.001 694,下降率为5.1%;线性插值填补法在缺失率为10%的情况下相较于1%时下降了0.813 341,下降率为13.8%,nMAPE均值下降了0.007 491,下降率为15.8%。

针对R23测点数据集,真实的填补情况如图6所示。

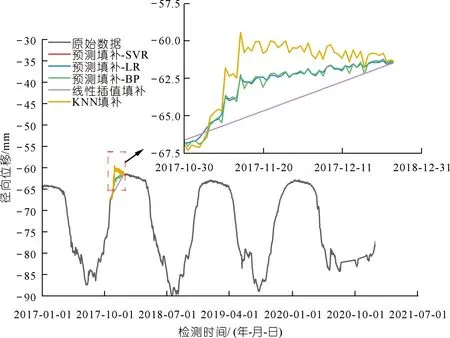
图6 实测缺失数据集不同填补算法的填补效果对比Fig.6 Comparison of the filling effect of measured missing data sets by different filling algorithms

依据图6可知,本文提出的填补算法可有效还原缺失值的真实分布情况,且较好地还原了数据本身的周期性。而线性插值填补法等传统算法,仅利用缺失值前后的数据进行回归,无法挖掘出测点内部的周期性以及测点间的相关性,导致缺失值填补效果较差。

4 结 论

(1) 本文通过研究分析现有大坝安全监测数据集中缺失值分布情况,总结提出了数据集中主要的缺失类型。

(2) 基于测点间相关度的评判依据,提出了一种融合多测点数据相关性的缺失值填补新算法,该算法利用已有的预测模型作为数据填补的来源,通过反复迭代计算,获得较高的数据填补质量。

(3) 试验结果表明,本文所提算法相较于其他填补方法,针对不同类型缺失值数据集在RMSE均值上至少提升15%,nMAPE均值至少提升10%,能很好地还原缺失值的真实变化趋势,满足大坝安全监测要求。