土质心墙坝防渗墙顶部土体剪切带模拟研究

黄 宁,何 蕃 民,吴 梦 喜

(1.四川交通职业技术学院 道路与桥梁工程系,四川 成都 611130; 2.中冶成都勘察研究总院有限公司,四川 成都 610023; 3.中国科学院力学研究所,北京 100190; 4.中国科学院大学,北京 100049)

0 引 言

建造在深厚覆盖层上的土质心墙坝,坝基中常设置混凝土墙防渗。防渗墙与其上部坝体的土质心墙多采用插入式或廊道式连接[1]。刚性、薄而深的防渗墙夹在柔性覆盖层土体之中,合理地确定混凝土防渗墙应力是大坝防渗墙设计的重要内容,也是一个难题[2]。

防渗墙在垂直方向上的受力主要包括:作用在防渗墙或廊道顶部的土压力,墙身因两侧土体与墙体差异沉降而产生的侧壁摩擦力以及墙身的自重。从垂直方向看,防渗墙是偏心受压结构[2]。防渗墙在水平方向的作用力主要是墙两个侧面的水压力和土压力。由于防渗墙一般嵌入岩槽一定深度,因此其周边嵌入基岩的墙身水平方向位移受到较强约束。从水平方向看,防渗墙属于周边受约束的薄板,墙身的弯矩对防渗墙的应力影响很大[2-3]。土对防渗墙的作用力(包括防渗墙上的土压力与摩擦力)引起防渗墙变形,防渗墙变形又影响作用力的大小。墙和土是相互作用的一个体系,合理的计算方法必须将地基、防渗墙和坝体视为整体,用变形协调将三者联系起来[3]。覆盖层和坝体填筑土体的变形模拟,以及土与结构相互作用的模拟,两者均对防渗墙应力的合理计算产生重要影响。

土与结构相互作用的模拟,包括土与结构接触面上的不连续变形(剪切滑移和接触面张开)和结构物上部土体中剪切带的模拟。对于土与结构物的接触面,通过在土与结构物界面上设置接触面单元,如Goodman接触面单元[5]和Desai接触面单元[6],可以较好地模拟出土体与结构接触面上的非连续变形特性。对于土体内部剪切带的模拟,则起源于边坡稳定的有限元法研究[7]。土体内部剪切带的萌生与扩展是导致边坡滑动失稳的原因。20世纪60年代,Skepmton[8]和Bjerrum[9]对超固结黏土边坡渐进破坏问题,最先开启了剪切带扩展理论的研究。在此基础上Palmer[10],Rice[11-12],Puzrin等[13]基于断裂力学方法推导了各种情况下台阶状边坡中预设滑裂面的扩展条件,而土体中剪切带的萌生条件可由Mohr-Coulomb强度理论描述已经成为共识[14]。

早在1980年,Johnson等[15]就意识到,使用连续插值函数的传统有限元方法(位移法)并不是特别适合于塑性问题的求解,因此建议修改形函数使非连续位移可以被更好描述。在四边形单元中嵌入非连续线来模拟剪切带的方法[16-17]被提出。越来越多的研究采用在单元内嵌入不连续位移场的处理方法,允许单元产生较大畸变,以便模拟整体的强不连续位移场[18-21]。大量的研究比较了在单元中嵌入非连续位移的各种方法[22-25],这些方法用于模拟因剪切带形成的不连续位移场在网格依赖性和应力锁死方面较弥散裂纹模型有改进。然而,这些方法对于不连续位移场的描述均基于网格单元,剪切带尖端难以确定,也就无法描述和揭示由土体应变软化特性导致的尖端应力集中和重分布对剪切带扩展过程和方向的影响[25]。

扩展有限元等方法[26-29]可将物体的材料非线性和土体结构的边界非线性区别对待,既可较好地描述内部运动的不连续位移场,又可相对独立地选择合适的本构模型,为剪切带扩展过程的模拟提供了强有力的技术支持。与单元内嵌入非连续方法相比,扩展有限元法网格依赖性较小,对剪切带形状和界面接触状态的描述更准确。这类方法有可能考察剪切带尖端应力集中对扩展过程和方向的影响,促进了已有剪切带扩展分析方法,并给剪切带扩展过程的模拟研究提供了新的思路。

土中剪切带扩展机理和模拟方法等方面仍有很多问题需要深入研究。由于涉及大变形、应变局部化[30]、非连续[31]等力学研究的前沿理论,相关的数值模拟方法并不成熟,也难以应用于土体非线性弹性数值计算体系,同时还存在如网格的依赖性[28]等问题,将这些数值模拟方法直接应用于实际工程还比较困难。

对于深厚覆盖层上的土质心墙坝中结构物顶部在坝体填筑过程中因差异沉降产生的土体内部剪切带,本文提出一种在可能出现剪切带的部位预设剪切面单元的方法,来探讨模拟土中剪切带及其扩展。此方法首先用于沟埋式涵洞顶部土压力离心机试验算例[30],验证方法的合理性后,再给出了用于模拟土质心墙坝中结构物顶部土体内非连续变形的算例。根据大渡河、瀑布沟等深厚覆盖层上的高心墙堆石坝应力变形计算与实际监测[32-33],常规数值分析计算防渗墙应力明显被高估,因此有必要发展防渗墙顶部土体剪切带的模拟技术,提高其计算分析精度。

1 剪切带变形模拟方法

1.1 防渗墙顶部土体剪切带产生机理

防渗墙的变形模量比覆盖层和坝体填筑土体大几个数量级,因而防渗墙身的垂直压缩量远远小于两侧的覆盖层。如图1所示,在大坝填筑过程中,在上部填土的自重作用下覆盖层和防渗墙之间的沉降存在较大的差异,墙土之间会产生剪切滑移;当填筑体达到防渗墙的顶部后,其上部土体的填筑将防渗墙顶部覆盖起来,随着坝体填筑高程的继续上升,防渗墙顶部两侧土体的沉降量将显著大于墙顶部正上方土体的沉降量(防渗墙或廊道的顶托作用),即防渗墙上部土体中会产生沉降量急剧变化的剪切带。底部设置刚性涵洞结构物填土的离心机试验表明[25,30],结构顶部土体内的剪切带(滑移带)是真实存在的,滑移带两侧的差异沉降在结构顶部最大,向上逐步减小,并在上部出现0差异沉降的等沉面[4]。通过上述分析可见,土质心墙坝防渗墙顶部土体剪切带相对确定,发生的起始地方一般在防渗墙顶部,但剪切带不一定贯穿结构物上部的全部土体,即滑移带的结束位置是未知的。

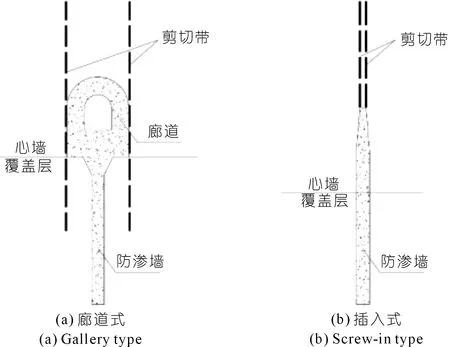
图1 防渗墙顶部土体的变形示意Fig.1 Soil deformation on top of cut-off wall

1.2 剪切面单元

如图2所示,在等厚度薄层四边形单元(本文以二维为例)中,坐标系XOY为整体坐标,坐标系X′O′Y′为局部坐标,坐标轴X′方向为剪切带土体滑移方向(简称“切向”),坐标轴Y′方向为法向。

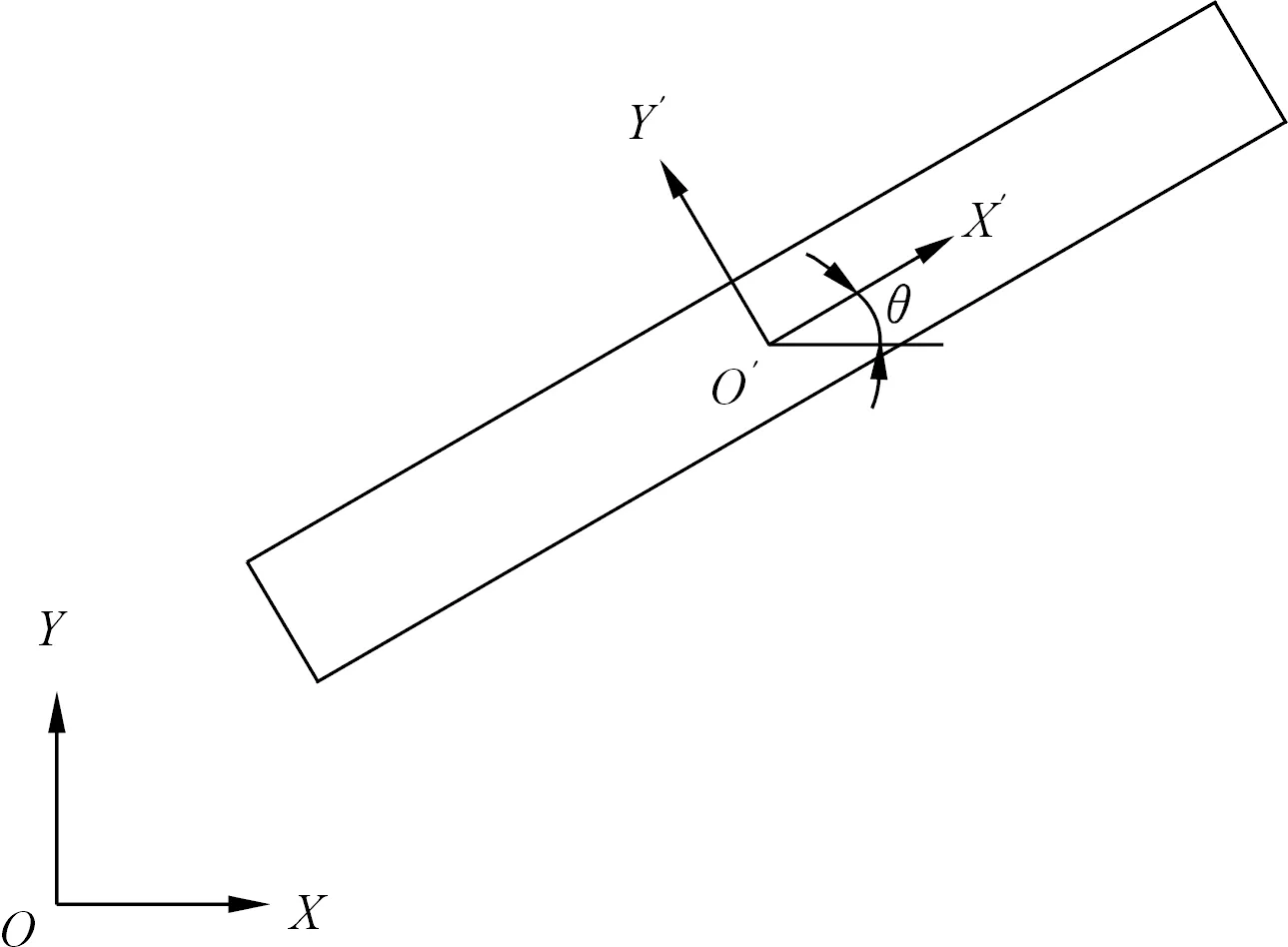
图2 剪切面单元(局部坐标与整体坐标)Fig.2 Shear band element(local coordinate and global coordinate)

在局部坐标系下,当前计算步i的剪切面单元应力应变关系与普通的实体单元在形式上基本一致,具体表达式如下(省略了计算步下标i):

(1)

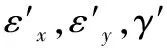
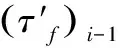
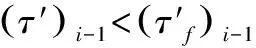
(2)

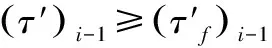
(3)

根据有限单元法基本理论[34],局部坐标系下剪切面单元节点力{F′}e与节点位移{δ′}e之间的平衡关系可以写成:

{F′}e=[K′]e{δ′}e

(4)

式中,[K′]e为剪切面单元的刚度矩阵,采用式(5)计算。

[K′]e=∬Ω[B′]T[D′][B′]dΩ

(5)

式中:弹性矩阵[D′]=[C′]-1,[B′]为平面应变矩阵。

1.3 整体坐标系下剪切面单元刚度矩阵

剪切面单元节点力、节点位移在整体坐标与局部坐标系下满足下列关系[35]:

{F′}e=[R]{F}e, {δ′}e=[R]{δ}e

(6)

式中:{F}e,{δ}e分别为整体坐标系下剪切面单元节点力和节点位移;{F′}e,{δ′}e分别为局部坐标系下剪切面单元节点力和节点位移。对于图2所示的剪切面单元(四节点矩形单元),单元旋转矩阵[R]为

(7)

式中,旋转矩阵[α]写成

(8)

将式(6)代入式(4),整理后为

{F}e=[K]e{δ}e=[R]-1[K′]e[R]{δ}e

(9)

根据式(9),可得出整体坐标系下剪切面单元刚度矩阵如下:

[K]e=[R]-1[K′]e[R]

(10)

整个剪切面单元刚度矩阵计算流程如图3所示。

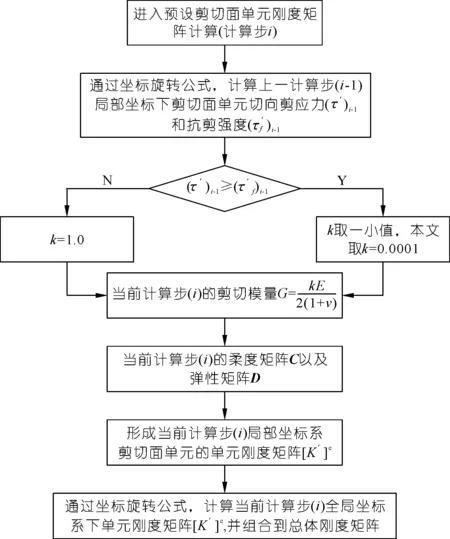
图3 剪切面单元刚度矩阵计算流程Fig.3 Calculation flow of stiffness matrix of shear band element

2 涵洞算例

2.1 计算模型及参数

以沟埋式涵洞土压力室内试验[30]进行模拟分析,并将模拟结果与试验结果进行对比。如图4(a)所示,矩形沟槽宽B为0.5 m,高为1.1 m;涵洞高h、宽D均为0.1 m。模型填料为中细砂,容重14.0 kN/m3,内摩擦角31°,黏聚力为0,压缩模量0.5 MPa,泊松比0.21。模型有限元网格划分如图4(b)所示。为探讨剪切面单元的设置高度,初始时在涵洞顶部土体内沿涵洞两侧竖直向上设置两个贯穿这个砂土层的剪切面单元,单元厚度为1 cm。剪切面单元弹性模量E、泊松比v与填料取值一样,而剪切模量G按式(2)、(3)计算。

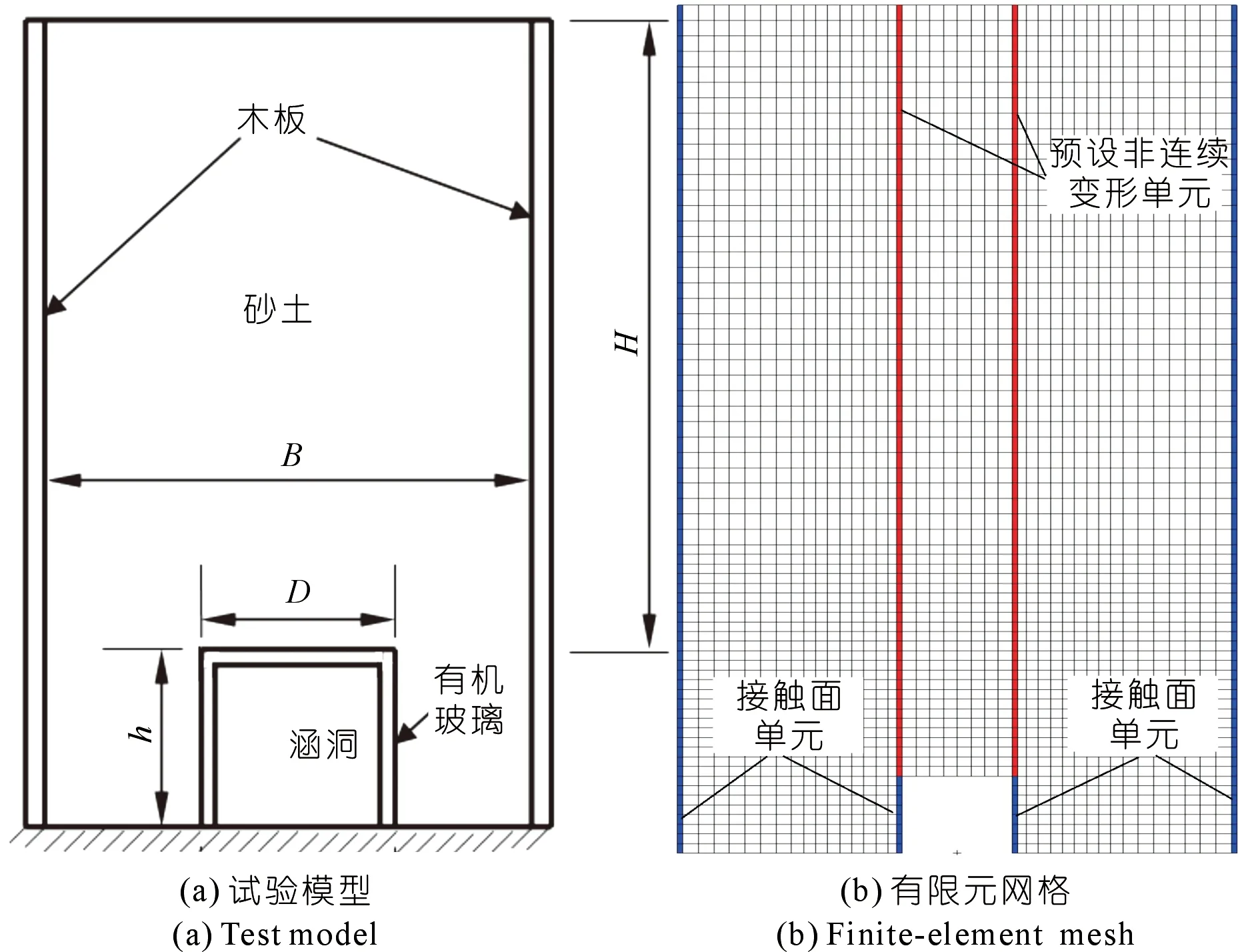
图4 矩形沟埋式涵洞Fig.4 Rectangular trench buried culvert

在细砂与涵洞、木板的交界面上设置无厚度的Goodman接触面单元[5],接触面单元的本构关系采用Duncan-Clough双曲线模型[31],计算参数见表1。

表1 涵洞算例接触面计算参数Tab.1 Calculation parameters of contact element of culvert calculation example

2.2 涵洞周围土体位移

涵洞顶部土体内不设和设置剪切面单元计算得到土体的竖向位移如图5所示。由图5可见,两种方法计算得到的最大竖向位移都发生在土层的中部,最大值分别为7.33 mm和7.40 mm。设置剪切面单元计算的沉降最大值更大,且得到的涵洞顶部土体等值线明显更加密集,剪切面单元(图中红色虚线)两侧错动位移明显,错动位移达到2 mm。而不设置剪切面单元的计算模型则无法反映出土体内部剪切带的错动变形。

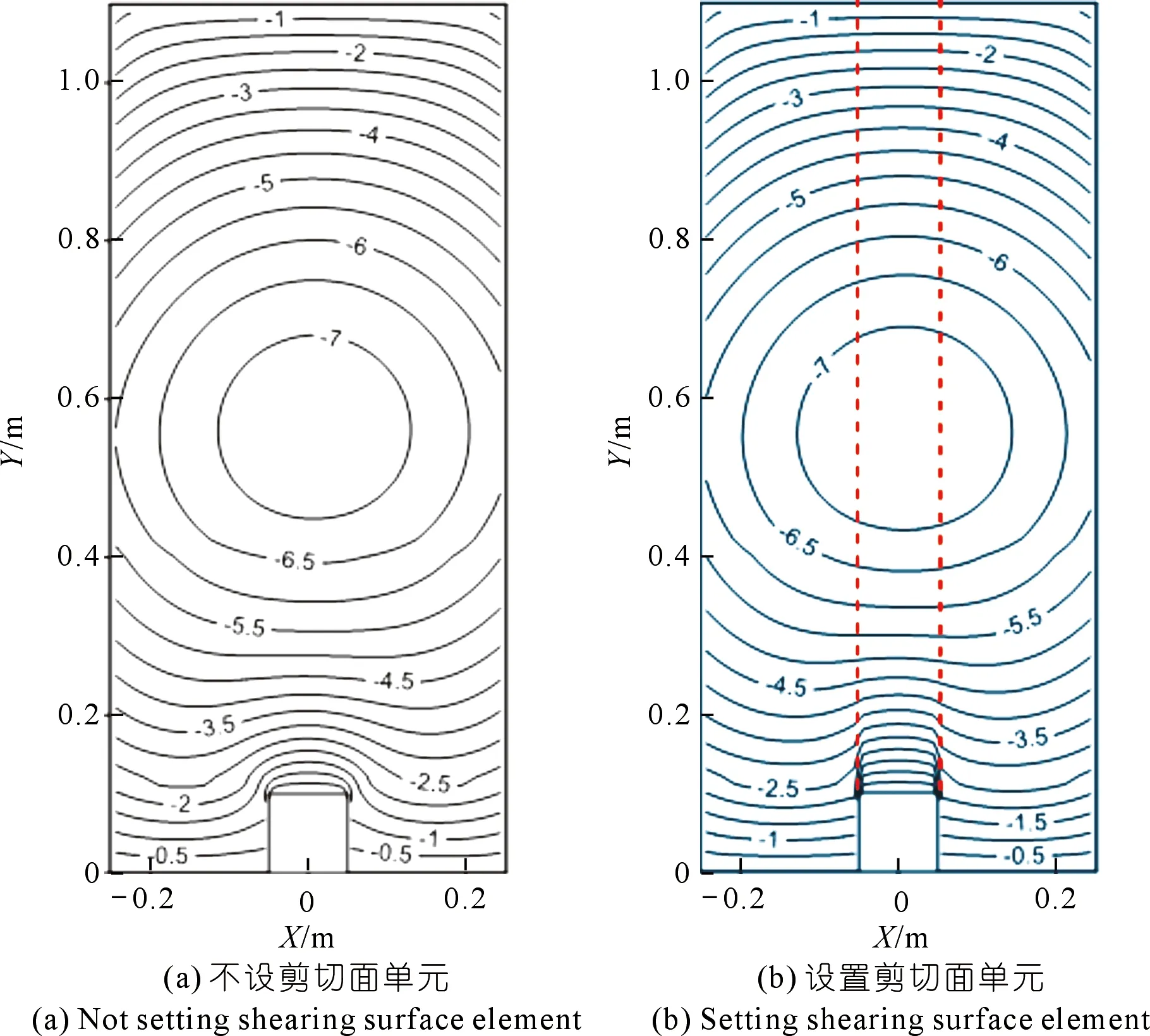
图5 土体的竖直方向位移(单位:mm)Fig.5 Vertical displacement of soil

绘制涵洞顶部剪切面单元两侧土体沉降差与土体高度关系曲线,如图6所示。由图6可知,越靠近涵洞顶部沉降差最大(沉降差为2.16 mm),随着土体高度增加,沉降差逐渐减小,当土体高度为0.275 m时,沉降差降低至0.01 mm以内,真实再现了试验中观测到的等沉面[4]。由此可见,预设剪切面单元具备模拟剪切破坏前土体连续的变形特性,以及土体剪切破坏发生后剪切带土体的错动变形特性,且两种变形状态模拟转换在计算过程中自动判别。

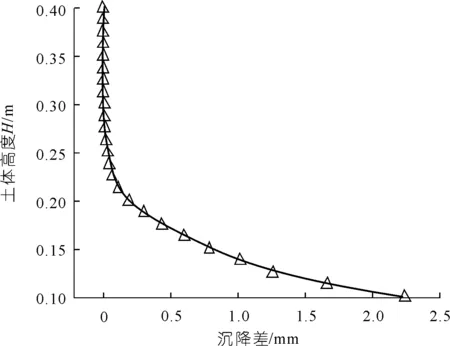
图6 涵洞顶部土体沉降差Fig.6 The subsidence difference of soil on top of culvert

2.3 涵洞顶部土压力

填土高度为1.0 m时涵洞顶部竖向土压力分布情况如图7所示。可以看出,设置与不设置剪切面单元计算得到的涵洞顶部土压力值平均分别为15.48,16.36 kPa,分别较试验值(15.35 kPa)大0.8%,6.2%。

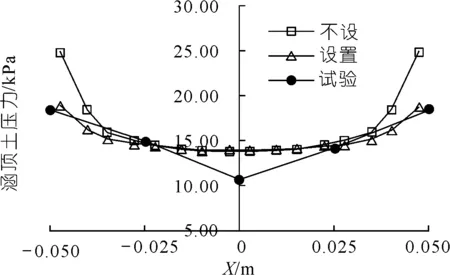
图7 涵洞顶部竖向土压力Fig.7 Vertical earth pressure on top of culvert

从土压力的分布来看,在涵洞顶部中间两侧各3.5 cm范围两种计算方案得出的土压力值基本重合,而越靠近涵洞左右两端,土压力数值差值越大,说明应力集中效应更加明显。将涵洞顶部左右端土压力值列于表2。由表2可以看出,不设置剪切面单元计算结果要比试验值更大,最大高出35.0%,由此可以看出仅仅设置土与结构接触面单元是不够的;设置剪切面单元计算结果更接近试验值,计算得出土压力值比试验值,最大高出仅为2.4%。由此可见,设置剪切面单元计算结果更接近实际值。

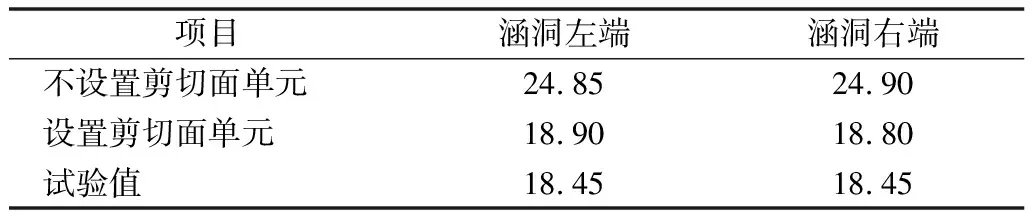
表2 涵洞顶部土压力值比较Tab.2 Comparison of earth pressure on top of culvert kPa

3 典型土质心墙坝

3.1 计算模型及参数

以一个典型土质心墙坝作为工程算例(如图8所示)。大坝坝高100 m,覆盖层厚度为50 m。坝基覆盖层防渗采用厚1.4 m的混凝土防渗墙,墙底部嵌入基岩1 m,防渗墙上部与心墙的连接方式采用插入式连接,插入深度15 m;其中墙顶部5 m为变截面段,截面由宽1.4 m逐渐变为宽0.5 m;以下10 m及覆盖层中防渗墙厚度均为1.4 m。

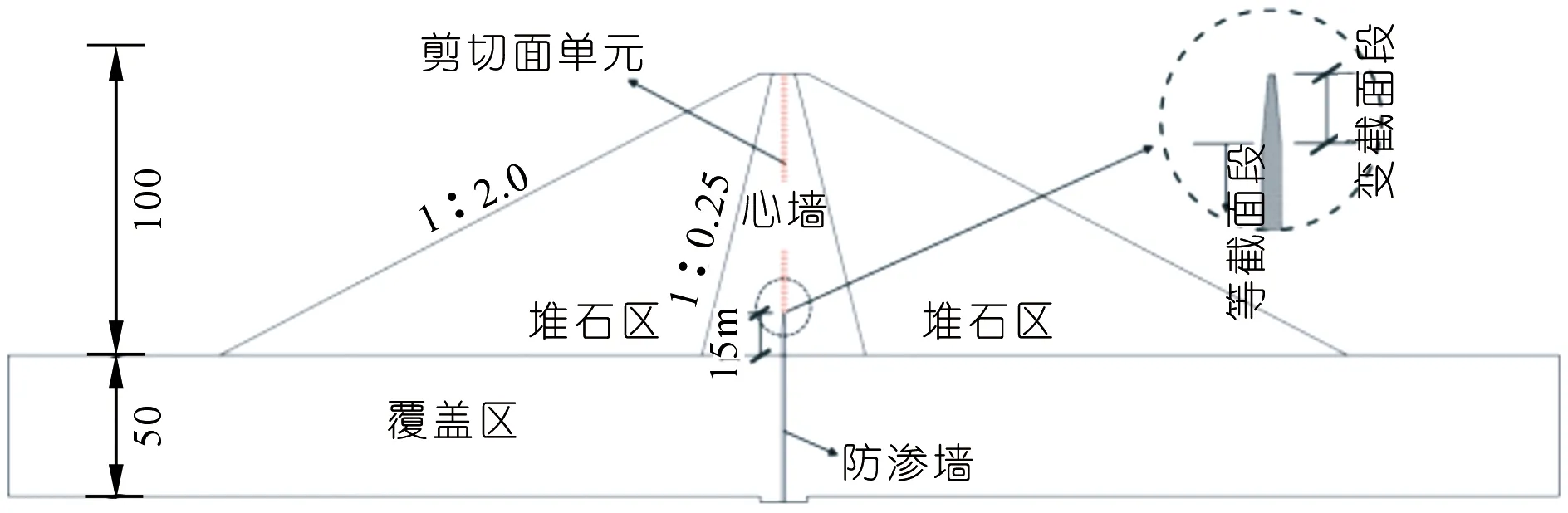
图8 典型土质心墙坝结构(尺寸单位:m)Fig.8 Structure drawing of typical core rockfill dam

计算模型采用平面应变模型,混凝土防渗墙和基岩均采用线弹性模型,混凝土防渗墙弹性模量取30 GPa,泊松比取0.17,基岩弹性模量取20 GPa,泊松比取0.28;筑坝材料采用邓肯E-v模型[36],切线变形模量Et和切线泊松比vt分别按式(11)、(12)计算,具体计算参数见表 3。

(11)

(12)

(13)

式中:K,n,Rf,G,F,D为试验参数;Rf为剪应力破坏比;c为黏聚力;φ为内摩擦角;pa为大气压力。

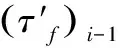
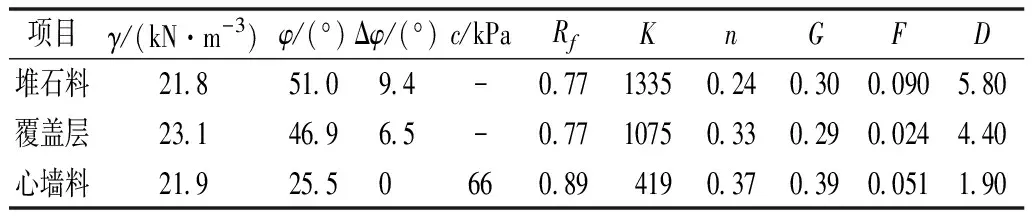
表3 心墙坝计算参数Tab.3 Calculation parameters of core rockfill dam

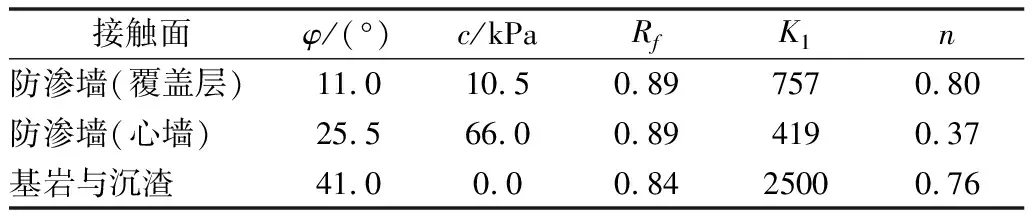
表4 心墙坝接触面计算参数Tab.4 Calculation parameters of contact element of core rockfill dam

在土体与混凝土防渗墙之间设置无厚度的Goodman接触面单元,单元的本构关系采用Duncan-Clough双曲线模型,计算参数见表 4。实际工程中,覆盖层中防渗墙周边裹挟着一层泥皮,而插入心墙的防渗墙周围是高塑性黏土,因此覆盖层中防渗墙接触面剪切参数中黏聚力值较心墙中的要更小些。

计算中不考虑水荷载。下文对比不设剪切面单元和设置剪切面单元两种方案的计算结果。

3.2 坝体位移

两种方案计算的坝体整体位移规律相同,坝体上下游水平位移基本对称,上下游坝体水平位移最大值分别出现在靠近堆石区中部建基面区域,最大值分别约为-0.20 m(向上游)和0.20 m(向下游);坝体最大沉降出现在心墙下部2/3部位,为1.22 m。防渗墙顶部设置剪切面单元时计算得到的坝体填筑完成后位移等值线如图9所示。

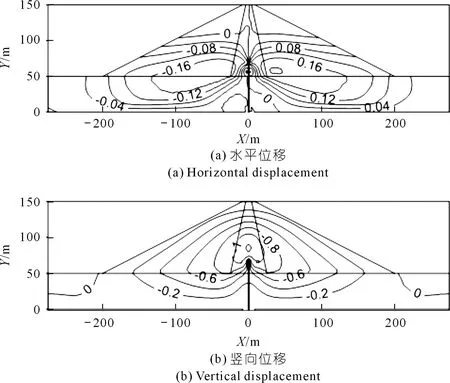
图9 坝体位移(单位:m)Fig.9 The displacement of dam

防渗墙顶部周围土体竖向位移计算结果、墙顶部土体非连续位移与高程关系分别如图10、11所示。可以看出,防渗墙顶部设置剪切面单元后,防渗墙两侧土体的竖向位移明显增大,使得墙顶两侧土体内出现高约10 m的剪切错动带;墙顶最大错动位移约为0.4 m。由此可见,防渗墙顶部非连续变形的模拟与否直接影响着两侧土体的变形计算结果。此外,图10显示了插入心墙土体部分周边土体沉降等值线较下部砂卵石层有更明显的集中,其因有二:① 防渗墙插入心墙周围设置有高塑性黏土,而高塑性黏土的黏聚力比覆盖层中的砂卵石层更大;② 防渗墙上部的变截面也导致局部土体沉降变形受限。

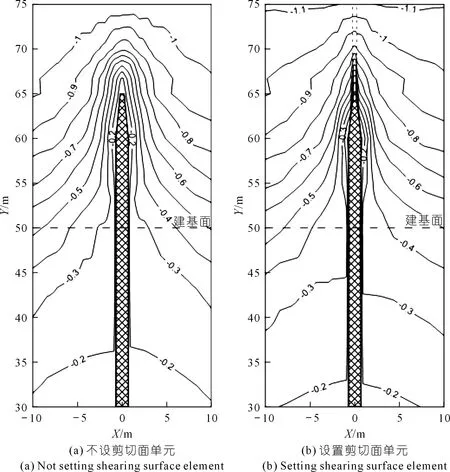
图10 防渗墙顶部周围土体竖向位移(单位:m)Fig.10 Vertical displacement of soil around the top of cut-off wall

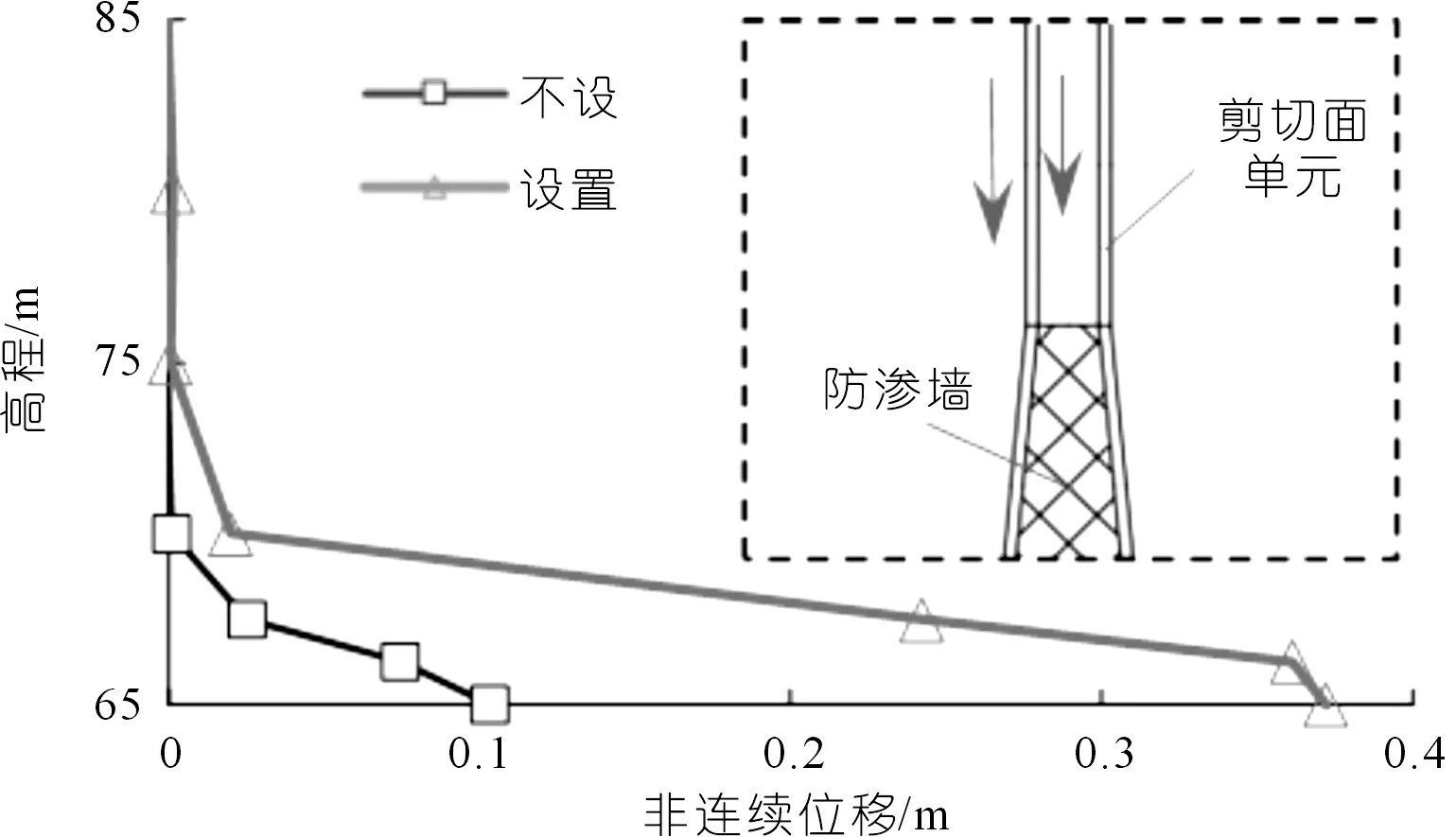
图11 防渗墙顶部土体中非连续位移Fig.11 Discontinuous displacement of soil on top of cut-off wall

3.3 防渗墙应力

防渗墙等截面段应力沿高程分布情况如图12所示。由图12可见,两种方案计算得到防渗墙的水平向正应力基本相同。对于竖直向正应力,两种计算方案均呈现出应力值随覆盖层深度增加而增大的趋势,应力值在8.0～22.0 MPa之间(见表5),与文献给出的部分100 m级心墙坝防渗墙应力监测值基本吻合[32]。从设置剪切面单元计算结果来看,设置剪切面单元的计算结果明显比不设时的计算结果小,其中墙体中部减小最大,最大减小了10.4%。

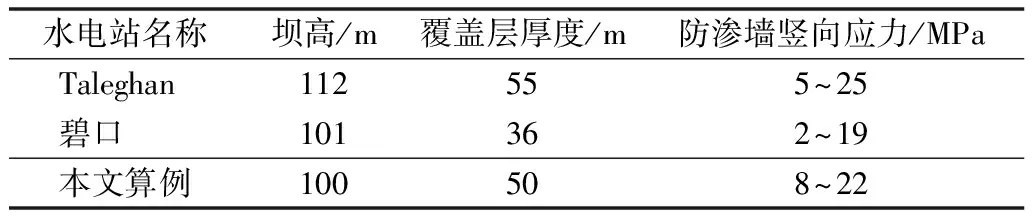
表5 100 m级心墙坝防渗墙应力监测值[32]Tab.5 Stress monitoring value of cutoff wall of 100 m core dams

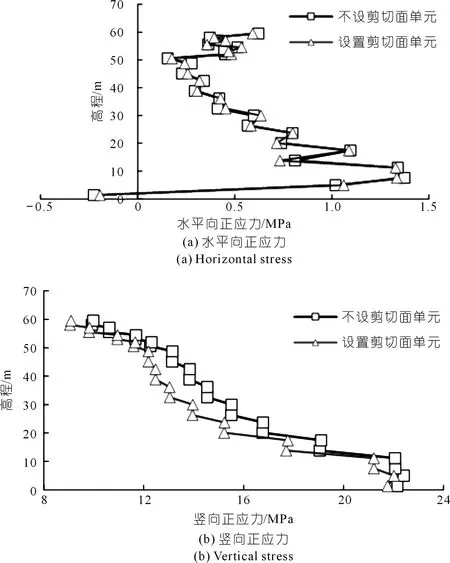
图12 防渗墙应力沿高程分布Fig.12 Stress distribution along elevation of cutoff wall

图13给出了防渗墙变截面段顶部竖向应力的结果。设置剪切面单元后,竖向应力平均值8.30 MPa,与不设时竖向应力平均值(11.93 MPa)相比,设置后计算结果小30.43%左右。可见,在土与结构相互作用时,若不考虑对结构物顶部土体的非连续变形进行模拟,结构的应力计算结果可能会与实际相差较大。

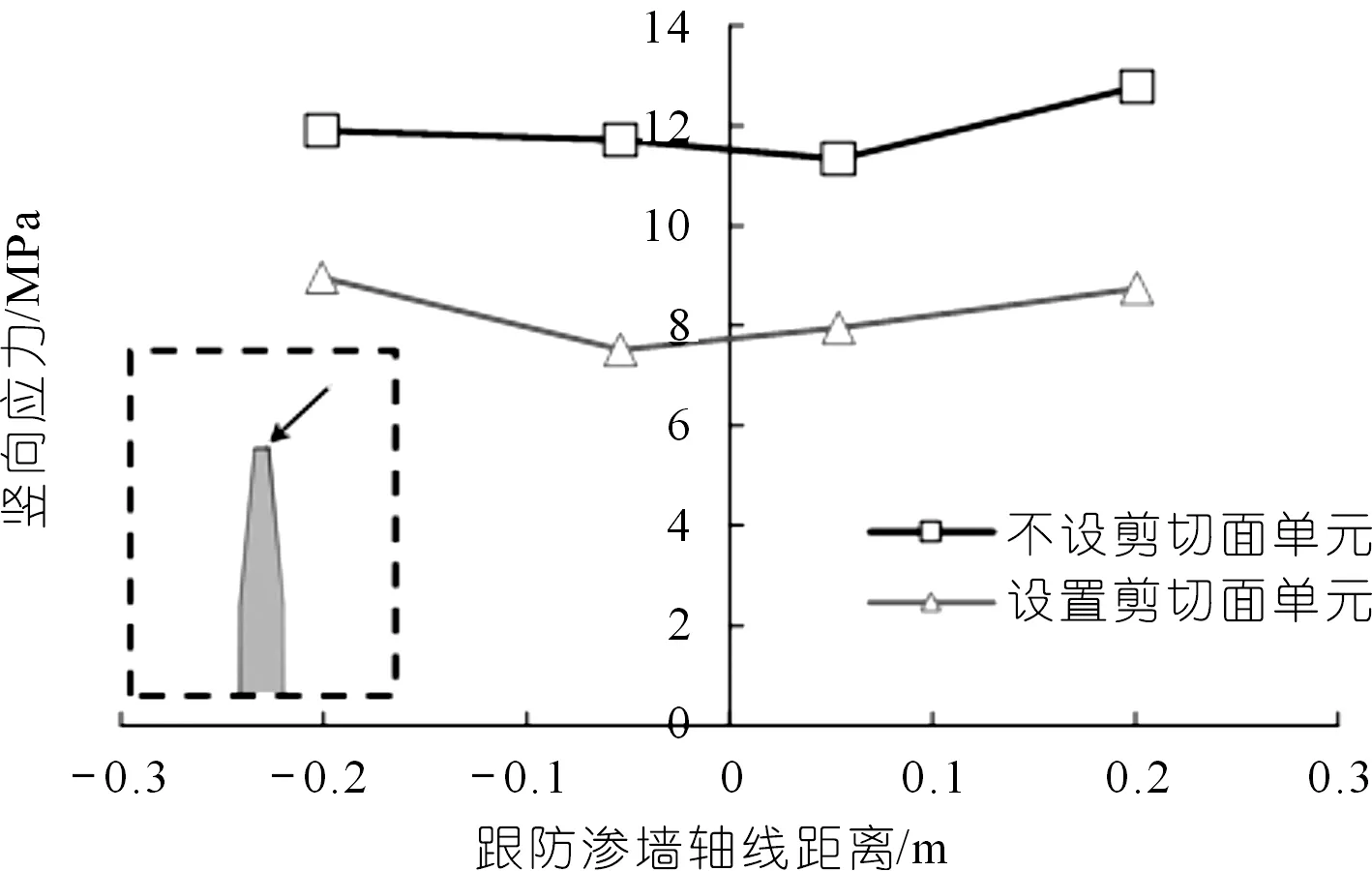
图13 防渗墙顶部竖向应力Fig.13 Vertical stress at top of cut-off wall

4 结 论

针对结构物顶部土体内部剪切带,如土质心墙坝混凝土防渗墙顶部土体在坝体填筑过程中因差异沉降产生的剪切带,本文提出了一种在可能出现剪切带的部位预设剪切面单元的方法来模拟,得出以下结论:

(1) 在填土1 m的矩形涵洞算例中,设置了剪切面单元后,计算得到涵洞顶部土体荷载结果分布更接近试验值。由此说明,本文提出的预设剪切面单元,既可以模拟普通土体单元连续变形特性,也可以模拟剪切破坏时剪切带土体的错动变形特性。

(2) 典型土质心墙坝计算结果表明,设置剪切面单元后,防渗墙两侧土体内出现高约10 m的错动变形区域,其中墙顶最大错动位移约为0.4 m。从防渗墙顶部竖向应力计算结果来看,设置剪切面单元计算得到竖向应力平均值约8.30 MPa,较不设时降低约30%。可见,在土与结构相互作用时,若不对结构物顶部土体的非连续变形进行模拟,结构的应力计算结果可能会与实际相差较大。

(3) 矩形涵洞算例和典型土质心墙坝工程算例的计算分析表明,在进行土与结构相互作用分析时,除应考虑土与结构接触界面上的非连续变形外,还应充分考虑结构物顶部土体的非连续变形对结构物应力变形特性的影响。本文提出的在可能出现剪切带位置预设剪切面单元的分析方法,克服了当前剪切带数值模拟中繁琐的计算流程以及对计算网格依赖性强等问题,且实现过程简单、高效,具有广阔的应用前景。