基于机器学习-CFD的明渠流速场预测模型
2023-09-25金诚,李博,杨岚斐,周新志
金 诚,李 博,杨 岚 斐,周 新 志
(1.四川大学 电子信息学院,四川 成都 610065; 2.四川大学 水利水电学院,四川 成都 610065; 3.成都万江港利科技股份有限公司,四川 成都 610000)
0 引 言
在灌溉明渠输水过程中,快速、简便而又准确地预测明渠中的流速场,对于提高水资源利用效率、明渠的设计与维护、流量测量等都有重要意义。大量学者对明渠断面流速分布规律进行了研究[1-2],他们普遍将明渠断面按照水力特性分成不同区域,并力图得到统一的数学方程来完整地描述流速分布规律。2000年,Sarma等[3]通过实验测量发现矩形明渠断面最大流速位置和宽深比的关联。此后,在Sarma的理论基础上,大量研究人员又进行了一系列有针对性的补充和改进[4-6]。2005年,Maghrebi等[7]根据最大熵原理和约束条件(质量、动量、能量等),提出了一种明渠速度分布公式。2015年,Bonakdari等[8]基于概率密度函数的tallis熵也提出了一种流速分布公式。
但是,对于输水水位变化较快的渠道,无法使用这些速度分布公式来实时预测不同水位下的断面流速场。其原因在于,这些速度方程的精度在很大程度上取决于其参数,这些参数只能通过经验或半经验的分析来估计。例如,紊流结构和边界剪应力是明渠流动中的基本问题,但即使使用复杂的紊流模型,也很难准确预测它们。在实际工程中,当渠道水位变化较大时,要将一种速度分布公式推广到不同水位情况下是困难的。要想实现依据明渠当前的水位快速预测断面流速场的目标,需要一种具有强大非线性映射能力和鲁棒性的模型。
近年来,在明渠断面流速场的计算问题中,各种机器学习模型得到了研究人员更多的关注和尝试,并取得了较为丰富的成果。2015年,Gholami等[9]采用基因表达式编程(GEP)模型对90°弯道内的速度场进行了预测,还将三维计算流体力学(CFD)和多层前馈人工神经网络(MLFF-ANS)应用于急弯水流深度和速度场的模拟[10];在2016年,Bonakdari等[11]介绍了一种新的混合遗传算法-人工神经网络(GA-ANN)来预测明渠枢纽处的复杂速度场,2020年他又提出了一种新的专家系统(SAELM)来对下水道内的速度场进行预测[12]。这些成果表明,机器学习方法在明渠流的相关问题上有良好的应用前景。但是据笔者调研,当明渠在输水过程中水位快速、大幅地变化时,对于如何实时地、准确地预测不同水位时的断面流速场这一问题,至今仍然没有公开的报道。
本文将机器学习方法与CFD方法结合,拟提出一种新的基于水位的明渠流速场预测模型构建方法。
1 试验明渠及测量方法
1.1 人民渠工程参数
试验对象为四川省都江堰灌区人民渠总干渠,其工程参数由人民渠渠首管理站提供,该渠如图1所示。线段AB为测流断面的位置,图2显示了渠道在线段AB处的横截面,其形状为等腰梯形,边坡角度α为135°。渠底宽度W为18.6 m,渠道的输水水位H变化较大,在0.5~3.3 m之间变化。

图1 人民渠图片Fig.1 Photo of Renmin channel
渠道输水过程中最小宽深比为5.6,是一条宽浅明渠。CFD建模部分为顺直明渠,长度为379 m,测流断面上游部分长度为299 m。此外渠道输水过程中平均流速在0.51~1.82 m/s之间,相对于渠道的顺直长度而言,水流速度缓慢。
因此,水流在到达测流断面之前,流态已经经过了充分发展,达到了稳定状态。即位于测流断面下游的各断面,流速分布高度一致,不受上下游未知边界效应的影响。测流断面的流速分布可以代表其下游渠道的流速分布。
1.2 真实流速数据的测量方法
流速数据的测量在测流断面AB上进行,从左岸x=-9.3 m至右岸x=9.3 m设立了7个垂直轴。根据渠道水位的不同,选择一点法、两点法、三点法进行流速的测量,即以相对水深h=(1-y/H)为标准,一点法在h=0.6的位置布置测点;两点法在h=0.2及h=0.8的位置布置测点;三点法则是在h=0.2,0.6,0.8的位置布置测点,如图2所示。
当人民渠的水位在0.5~1.5 m间变化时,使用一点法对每种水位的7个测点进行流速测量,共计测量11种不同水位,得到了77组测流流速数据;渠道水位在1.5~2.15 m间变化时,选取两点法对每种水位的14个测点进行流速测量,共计测量5种不同水位,得到了70组测流流速数据;渠道水位在2.15~3.3 m间变化时,使用三点法对每种水位的21个测点进行流速测量,共计测量11种不同水位,得到了231组流速数据。
测量仪器为LS1206B型旋桨式流速仪,如图3所示,该流速仪的全线相对均方差小于1.5%,相对误差小于5%,测量精度满足工程要求。

图3 LS1206B型旋桨式流速仪Fig.3 Rotor-type current meter of LS1206B
每次测量时,仅将该流速仪布置在一个测点,等到转子的转速稳定后,每隔10 s读取一个该点流速值。每个测点共读取3个流速值,并取平均值作为该点最终的流速值。使用该旋桨流速仪测量全部测点,得到全部378组流速数据。
2 研究方法
使用本文方法建立人民渠总干渠的“水位-流速场”实时预测模型的步骤如图4所示。
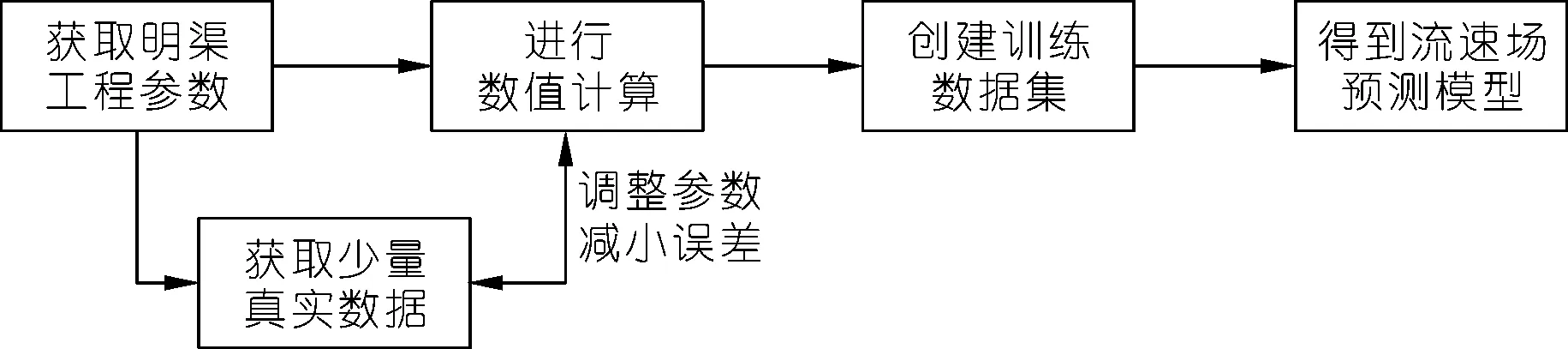
图4 流速场预测模型构建流程Fig.4 Construction process of flow velocity field prediction model
(1) 获取明渠工程参数。测量明渠的工程参数,如最大和最小水位,明渠形状参数等,由渠首管理站提供。
(2) 获取少量真实数据。在最高水位和最低水位间,在渠道的测流断面上获取少量流速数据。该工程中渠首管理站已经测量了27组水位流速数据,选取其中22种水位作为“仿真水位”。
(3) 数值计算。当渠道处于这些“仿真水位”时,根据明渠的工程参数,选择合适的方法对渠道进行CFD仿真。并根据实测流速数据,调整CFD仿真计算的参数,使仿真结果足够准确。
(4) 创建训练数据集。利用渠道在这些仿真水位时的CFD仿真结果,制作训练数据集。
(5) 构建流速场预测模型。构建一个自适应差分进化的极限学习机模型(SaDE_ELM模型),使用创建的训练数据集训练SaDE_ELM模型后,即为该明渠的“水位-流速场”实时预测模型。
成功构建该明渠的“水位-流速场”实时预测模型后,向该模型输入任意一个水位(在此水位下可以没有任何测量和仿真数据,但是此水位必须在该渠最大水位和最小水位之间),模型都能快速、准确地预测出该明渠此时的断面流速场。
2.1 数值计算
根据提供的工程参数,本文使用如下CFD方法对该段渠道进行仿真。
2.1.1湍流模型
选取标准k-ε模型和重组化群k-ε模型(RNGk-ε模型)分别封闭雷诺平均(RANS)方程,对比评估了各数值模型的模拟效果。在标准k-ε模型的基础上,基于重整化群理论,有效黏度μeff为
(1)
据此得到和标准k-ε模型相似的RNGk-ε模型为
(2)
式中:αk和αε表示湍流动能和耗散率的有效湍流普朗特数的倒数,其余参数含义见参考文献[10]。
对于顺直明渠,标准k-ε模型和RNGk-ε模型的模拟结果相差不大,但是RNGk-ε模型收敛速度更快而且误差更加稳定[13],因此选用RNGk-ε模型来封闭RANS方程。此外,采用VOF法来处理自由液面,即通过建立固定的欧拉网格,计算每个网格中流体体积与网格体积的比值来模拟和推导自由水面。
2.1.2边界条件及网格划分
对图1所示的“CFD建模”段渠道中水域和空气域都设置为计算域,如图5所示。图中,XOY平面是测流断面;水域的高度(H)每次仿真时设置为不同的水位,但是空气域和水域的高度之和每次仿真始终恒定为6.6 m。
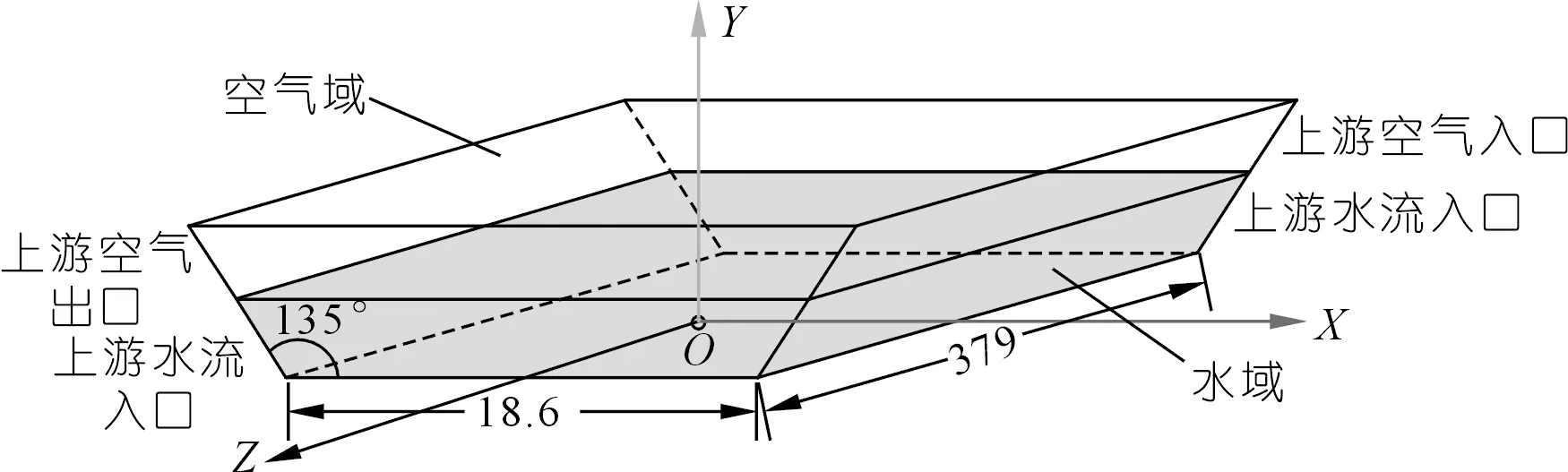
图5 计算域示意(单位:m)Fig.5 Diagram of calculation domain
对于边界条件,上游水流进口设置为流速进口,为渠道的平均流速,由上游流量和渠道的横截面面积计算得到;上游空气入口为质流进口;下游水流出口采用质流出口;下游空气出口采用压力出口;湍流强度设置为5%;外部自由边界设置为压力进口边界,为一个标准大气压;渠道底面和边壁都为水泥壁面,设置为无滑移的静态壁面,粗糙高度为0.46 mm,粗糙度常数为0.5。
对于变量的离散化,在顺直明渠模拟时采用体积力加权方法(Body Force Weighted)来对压力进行插值处理,其余变量均采用二阶迎风离散格式。对于压力-速度场的解算则采用PISO算法,其收敛性和计算速度均更优。
2.1.3网格划分与无关性验证
由于人工顺直明渠的计算域比较规则,使用六面体的结构化网格对其进行划分,可以节约时间成本。在渠道边壁附近(为了考虑黏性流动)和自由表面使用较为精细的网格;在其他区域,使用相对较大的网格。
为了找到最佳网格,分别使用了3种尺寸(粗网格、中等网格和精细网格)进行仿真实验。其中粗网格在X、Y和Z方向上网格单元划分规格为54×44×400;中等网格为93×66×800;精细网格为124×99×1200。
使用水位3.3 m(H=3.3 m)时的渠道进行对比试验,在该水位的数值模型中,使用上述3种网格划分进行了计算试验,统计3种网格计算结果和实测结果的相对误差En:
(3)
式中:Vi为该水位下各测速点的实测速度,Vr为该水位下各点计算速度,n为该水位下测量点号,N为该水位下测点个数。
计算相对均方根误差(RMSE)和平均相对误差(MARE)作为相对误差的评价指标,公式如下:
(4)
(5)
统计结果如表1所列。

表1 3种不同网格的计算误差Tab.1 Calculation error of 3 different size mesh
由表1可知,使用中等网格(网格数量为93×66×800,共有20 043 533个节点)时,计算结果与网格大小已经几乎无关。故决定计算域使用中等网格,划分效果如图6所示。
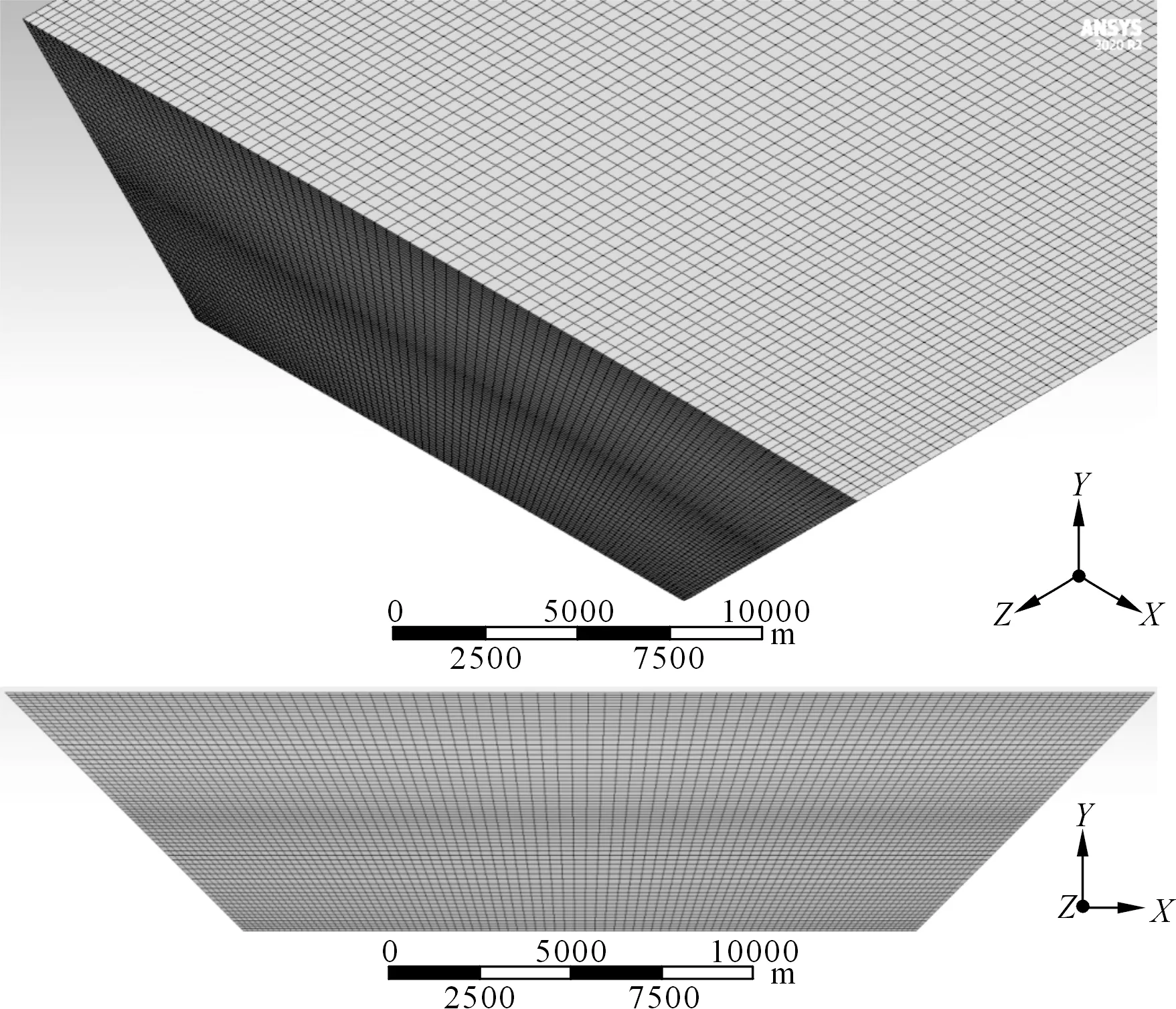
图6 中等网格划分效果Fig.6 Division effect of medium grid
2.1.4计算结果及误差分析
使用前述CFD仿真方法,对22种仿真水位进行仿真,不断修正边界条件的初始参数,使得仿真结果与真实数据的误差不断缩小。
由于渠道长度是渠道底宽的20.4倍,因此,由程科等[13]的研究可知,模型在测流断面的上游提供了足够的长度,流速场获得了充分发展,使得测流断面的下游流速场基本相同。这一结论也得到了CFD仿真的支持。当渠道水深为3.3 m时,测流断面及其下游的流速场如图7所示。
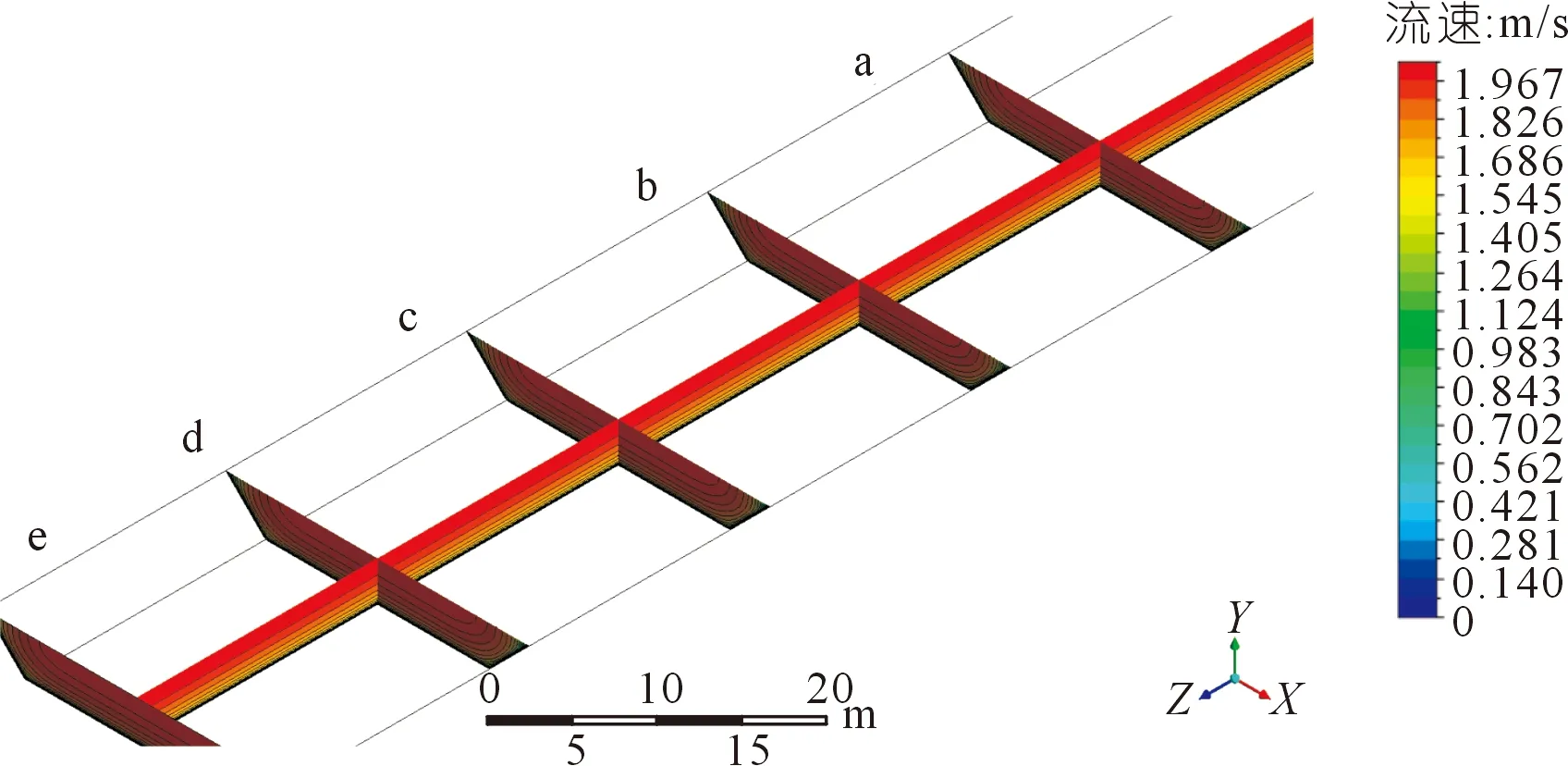
图7 测流断面下游渠道流速场Fig.7 Velocity field in downstresm channel of flow measurement section
图中,a断面为测流断面;b~e断面分别距离a断面20,40,60,80 m。各断面流速场(水域)如图8所示。
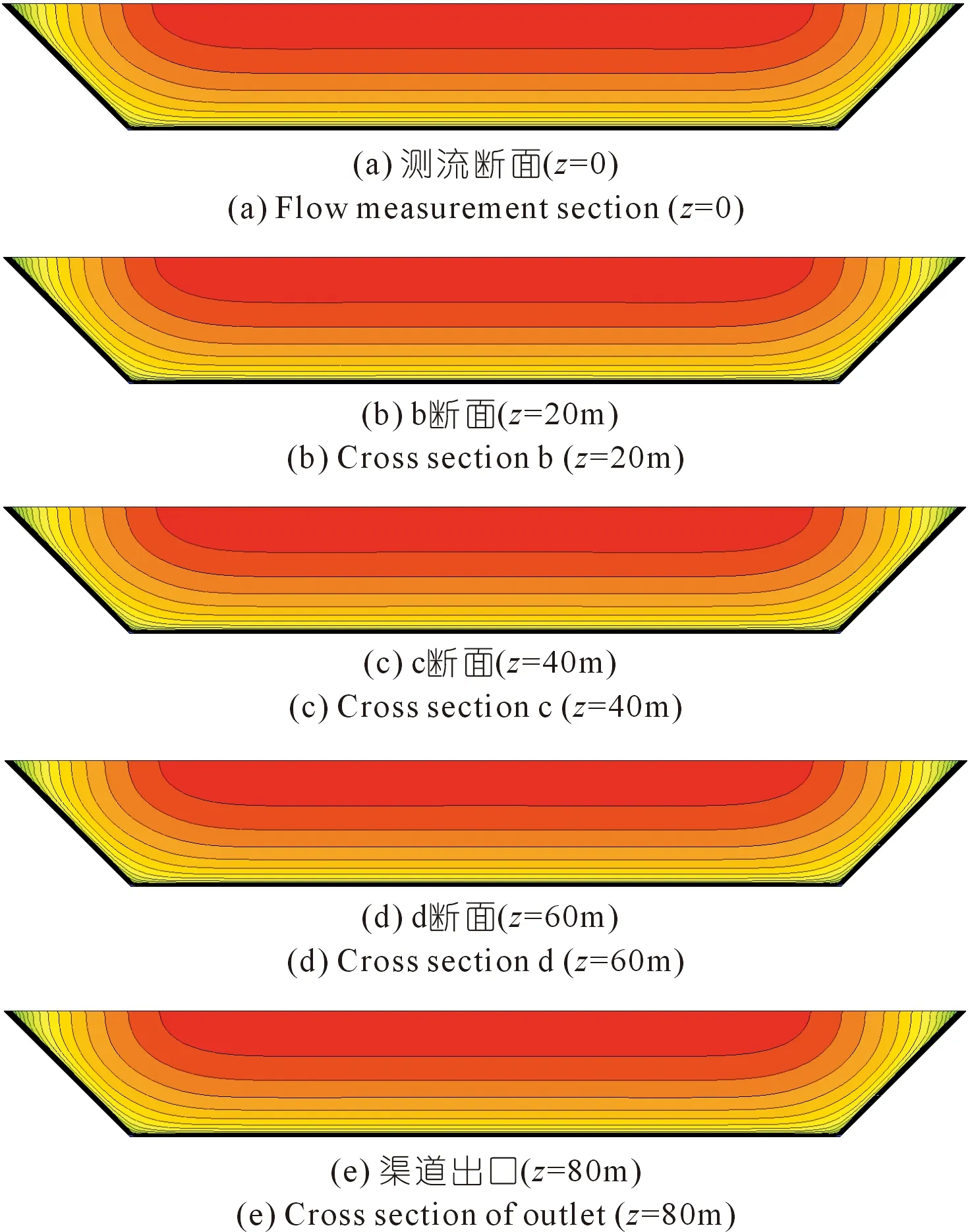
图8 5个断面的速度场Fig.8 Velocity field of 5 cross sections
由以上结果可以发现,渠道中最大流速出现在水面,并且在垂直方向上流速沿垂线单调下降,没有出现倾角现象。这是因为对于较宽浅的渠道,侧壁对流动的影响相对较小[8]。这表明人民渠总干渠是一条宽浅明渠。
为了定量分析CFD模拟的精度,统计了22种水位下各测点仿真计算结果与实测数据相对误差(En)的RMSE和MARE,结果如图9所示。
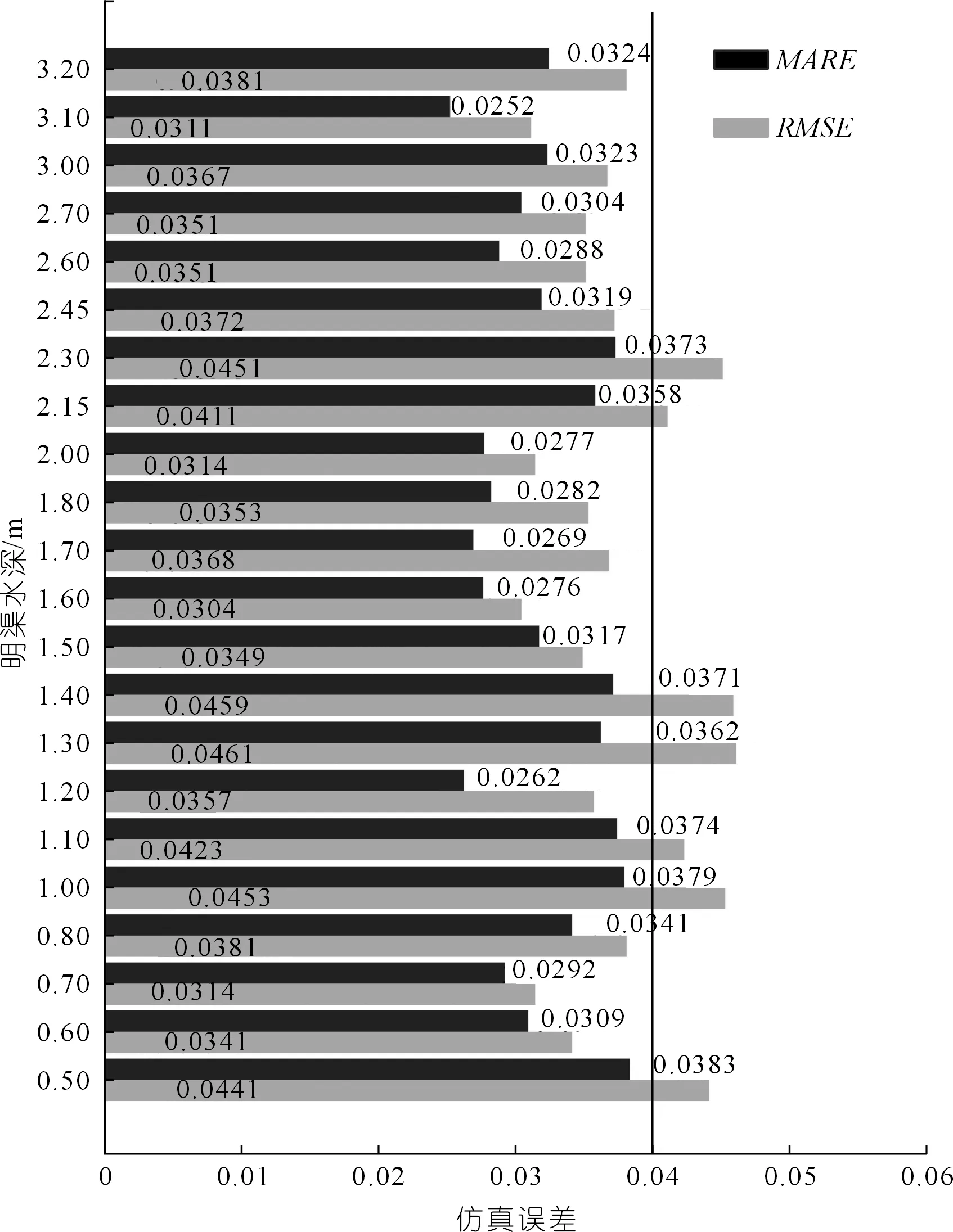
图9 22种水位下的CFD仿真结果误差Fig.9 CFD simulation results error under 22 water levels
在全部水位下,仿真实验结果的MARE均小于4%并且RMSE均小于5%,符合明渠测量统一标准(即|e|<5%)。这个结果充分表明:使用CFD模拟研究该类明渠具有极高的准确性。
2.2 训练数据集创建
制作训练数据集:将22种水位下CFD仿真实验结果作为实测数据集的补充,制作机器学习模型的训练集。各测点的数据是实测值,其余点的数据为计算值。将明渠此时水位(e1)、每个交点处的横坐标(e2)和纵坐标(e3)作为训练集输入数据,速度(v)作为训练集输出数据,产生训练集。
制作测试数据集:将5种水位(2.9,2.8,1.9,1.2,1.1 m)下的实测速度(见图2)作为神经网络的测试集,用来评价“水位-流速场”预测模型的精度。这5种水位分别使用了3种不同的测速标准,其中低水位(H=1.2,1.1 m)使用一点法测量;中水位(H=1.9 m)使用两点法测量;高水位(H=2.9,2.8 m)使用三点法测量。
2.3 流速场预测模型构建(SaDE_ELM)
为了实时预测输水水位快速变化的人工明渠流速场,本文充分结合极限学习机[14]和差分进化算法[15]的优势,并加上自适应机制,提出自适应差分进化的极限学习机(SaDE_ELM)模型作为“水位-流速场”预测模型。
2.3.1极限学习机(ELM)
极限学习机(ELM)具有训练效率高、超参数少、学习速度快等优点,其原理如图10所示。
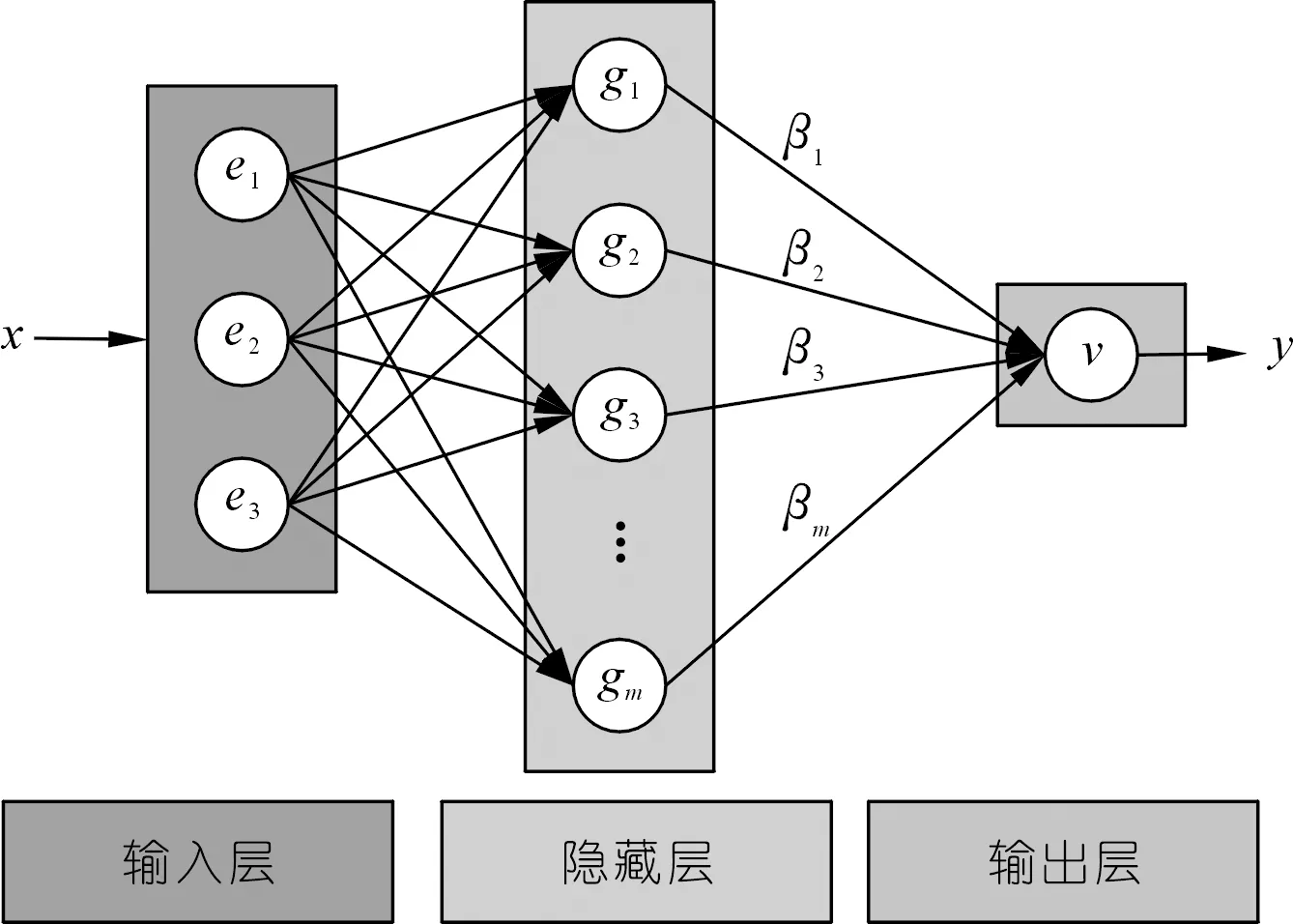
图10 ELM原理Fig.10 Schematic diagram of ELM
其核函数gm如下:
gm=Wm·x+bm
(6)
式中:Wm=[wm1wm2wm3]为第m个核函数的输入权重;bm为第m个核函数的偏置;x=[e1e2e3]T为输入的特征向量,则可计算隐藏层的输出向量为h=[g1g2…gm]。
对于一个极限学习机,若Wm和bm为已知的随机值,则对于输入的训练数据集(X,Y),X为包含k个相互独立的特征向量x的矩阵,可得极限学习机隐藏层的输出矩阵([h1h2…hk]T)为H。
此时可求ELM的隐藏层与输出层之间连接权重矩阵([β1β2…βm]T) 的近似解B,方法如下:
(1) 在本次研究中,由于训练样本数k远大于隐藏层神经元个数M,因此H是不可逆矩阵。此时采用最小二乘法求解矩阵H的Moore-Penrose增广逆(H†)。通常以正交法计算H†:
(7)
(2) 又已知输出层的目标输出矩阵([y1y2…yk]T)为Y,则有如下公式成立:
HB=Y
(8)
则解B为
B=H†Y
(9)
2.3.2使用SaDE优化ELM模型
在ELM模型中,隐藏层神经元核函数的参数(Wm和bm)是随机给定的,且模型的隐含层不使用大量神经元,这可能会使得模型无法取得全局最优解,导致计算精度不足。因此采用自适应差分进化算法(SaDE)优化ELM模型,步骤如下。
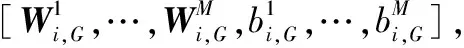
θi,1=θmin+rand(0,1)×(θmax-θmin)
(10)
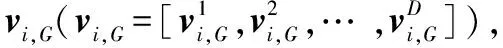
策略1:
(11)
策略2:
(12)
策略3:
(13)
策略4:
(14)
使用pl,G表示在第G代中应该选择策略l(l=1,2,3,4)的概率。根据概率pl,G,从这4种策略中选择第G代种群的变异策略。并且以如下方式更新概率pl,G:① 定义一个固定的迭代次数LP作为学习周期;② 当G≤LP时,pl,G=1/4,即该代种群中使用这4种策略的个体数量相同;③ 当G>LP时,pl,G的计算方法如下:
(15)
式中:nsl,g表示在第g+1代中得以保留的由第l策略生成的个体的数目;nfl,g表示在第g+1代中已经丢弃的由第l策略生成的个体的数目;ε是一个小的正常数值,以避免Sl,G=0。

(16)
式中:CR为发生交叉操作的判定值,是一个0~1之间的随机数;randj是属于第个特征值的交叉概率,也是一个0~1之间的随机数;jrand是一个属于[1,D]的随机整数,引入这个参数是为了确保μi,G中至少有一个特征出现了交叉操作。
(4) 评价操作。对于每个目标向量及其对应的试验向量,计算出每个个体θi,G的均方根误差RMSEi,G作为评价该个体的指标。
(5) 选择操作。用适应度函数进行选择操作,选择适应度值(RMSEi,G)较低的种群作为下一代的种群,选择方法如下:
(17)
式中:λ是预设的常数,用来控制淘汰率,越小意味着越多的个体会被淘汰。
重复步骤(2)~(5),直到达到目标或最大迭代次数。
3 结果与分析
成功建立人民渠的SaDE_ELM模型后,向其输入水位数据,就可以实时预测此时的断面流速场。为了更好地评价SaDE_ELM模型预测流速场的性能,以BP模型、ELM模型以及GAELM模型的表现作为参考。各模型的参数初始化设置如下:
(1) BP模型:神经元个数为100,激活函数为sigmod函数,损失函数为均方误差,优化算法为梯度下降法,训练次数为50次。
(2) ELM模型:节点个数为100,激活函数为sigmod函数。
(3) GAELM模型:个体参数与ELM相同。适应度函数为均方误差的倒数,种群数量为100,最大遗传代数设置为50,交叉概率为0.7,变异概率为0.01。
(4)SaDE_ELM模型:个体参数与ELM相同。适应度函数为均方误差的倒数,种群数量为100,最大优化次数设置为50,交叉率为0.5,比例因子为0.5。
向各模型中输入5种测试集的水位(2.9,2.8,1.9,1.2,1.1 m),观察模型预测的断面流速场是否符合一般规律,并统计模型预测速度与实测速度的误差。
3.1 流速场的流速分布规律
为了考察SaDE_ELM模型预测的流速场是否符合流速分布一般规律,使用4种模型和CFD方法分别计算5种测试集水位时的下游渠道的断面流速场,计算结果如图11所示。
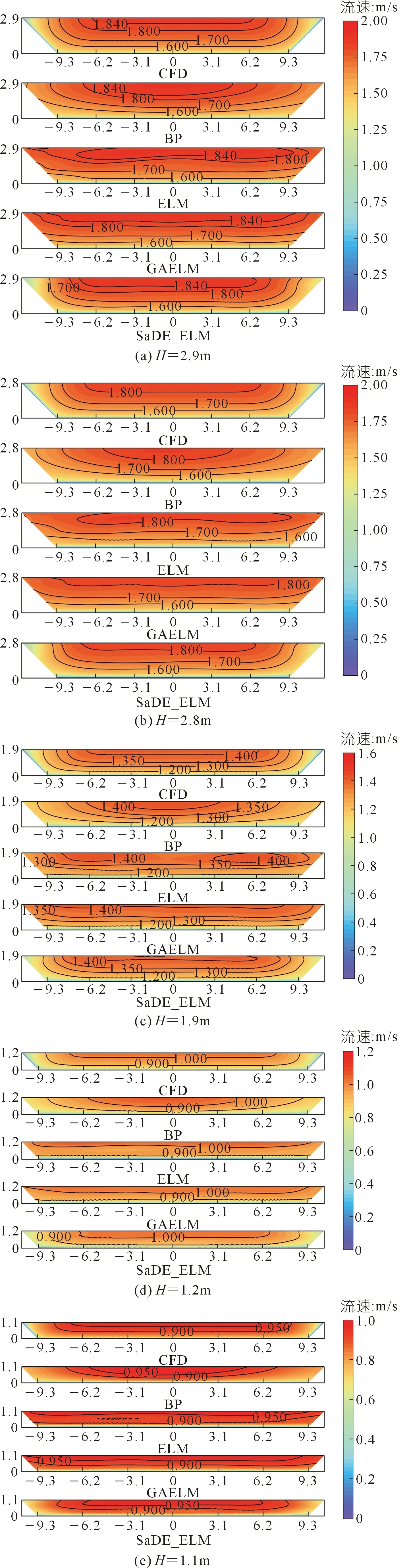
图11 不同测试水位下的速度场Fig.11 Velocity field under different test water levels
根据水力学的研究[16-17],人民渠是宽浅明渠,其流速分布一般规律概括如下:① 流速沿水平方向梯度小;② 流速沿垂直方向梯度大;③ 垂线上最大流速出现在水面,即没有倾角现象。
对于使用ELM模型、GAELM模型和BP模型计算的流速场,GAELM模型在渠道接近两侧壁的区域,流速下降缓慢,渠道的边壁效应不明显,其等速线都非常接近于一条条的“一”字形直线;而ELM模型水位为2.9,2.8 m和1.9 m时,出现“O”形等速线,最大流速在水面之下,有倾角现象;而BP模型的等速线是一层层的“C”形曲线,都不符合宽浅明渠流速分布的一般规律。
对于使用SaDE_ELM模型计算的流速场,在5种水位下,最大流速都出现在明渠的表面且沿垂直方向流速快速下降,没有出现倾角现象;在渠道中心区域,流速沿水平方向变化较缓慢;在接近边壁的边缘区域速度快速下降,边壁效应明显。符合宽浅明渠流速分布的一般规律。SaDE_ELM模型的等速线是一层层的“U”形曲线。
对于CFD方法得到的流速场,在5种水位下,最大流速都出现在明渠的表面;在接近水面和渠道中轴的区域,流速变化缓慢;在接近渠底和左右边壁时,速度迅速下降为零;流速场的等速线都是一条条平滑的“U”形曲线。流速场结果符合上述明渠流速分布的一般规律。
综上所述,ELM、BP和GAELM模型的计算结果和CFD仿真结果有较大差距,不符合宽浅明渠流速分布的一般规律,表明这3种模型在寻找全局最优解上有所欠缺。而SaDE_ELM算法对比CFD计算结果,无论是中心区域还是边缘区域,都有很好的计算效果,符合宽浅明渠流速分布的一般规律,SaDE_ELM与CFD的流速场高度相似,表明SaDE_ELM具有良好的泛化能力,在预测流速分布规律上,性能优异。
3.2 误差分析与比较
为了评价模型的预测精度,需要计算5种测试集水位时预测流速与实测流速之间的相对误差,计算方法如式(3),结果如图12所示。
在高水位(2.9,2.8 m)时,GAELM模型和ELM模型的误差在(-0.05,0.15)区间内波动;BP的误差值在(-0.05,0.05)范围波动,但有少数样本超过±5%的相对误差;SaDE_ELM的误差值在(-0.05,0.05)范围波动,且大部分相对误差的绝对值小于0.025,具有高精度和强稳定性。
在中水位(1.9 m)时,ELM模型和GAELM模型的误差很大,误差值在(-0.05,0.2)范围波动;BP模型的误差值在(-0.1,0.1)范围波动;SaDE_ELM模型误差值在(-0.05,0.1)范围波动,且大部分误差的绝对值小于0.05,其具有高精度和强稳定性。
在低水位(1.2,1.1 m)时,ELM模型和GAELM模型的误差非常大,而且误差值的波动性也非常大,误差值在(-0.05,0.35)范围波动;BP模型的误差值在(-0.05,0.15)范围波动;SaDE_ELM模型误差值在(-0.05,0.20)范围波动,其具有高精度和强稳定性。
为了更加准确地评价SaDE_ELM模型的预测精度和稳定性,需对预测流速与实测流速的相对误差进行定量分析。本文引入平均相对误差MARE(式4)、均方根相对误差RMSE(式5)和最大相对误差MAXE作为评价指标,结果见表2~4。
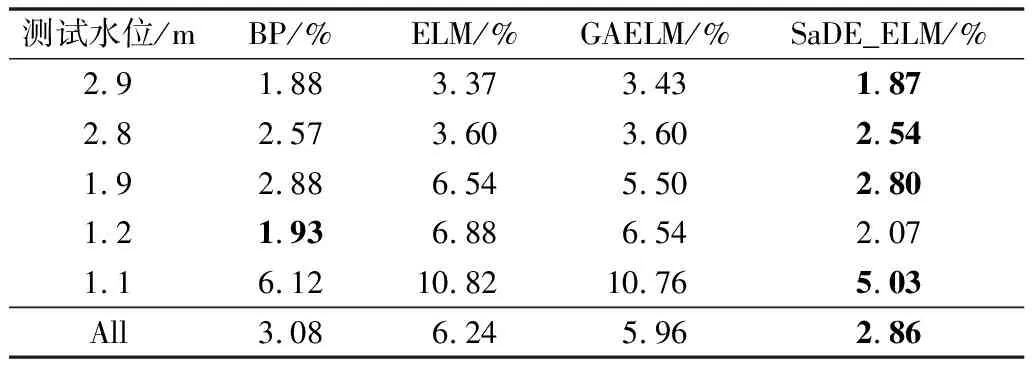
表2 不同模型的平均相对误差Tab.2 MARE of different models

表3 不同模型的均方根相对误差Tab.3 RMSE of different models
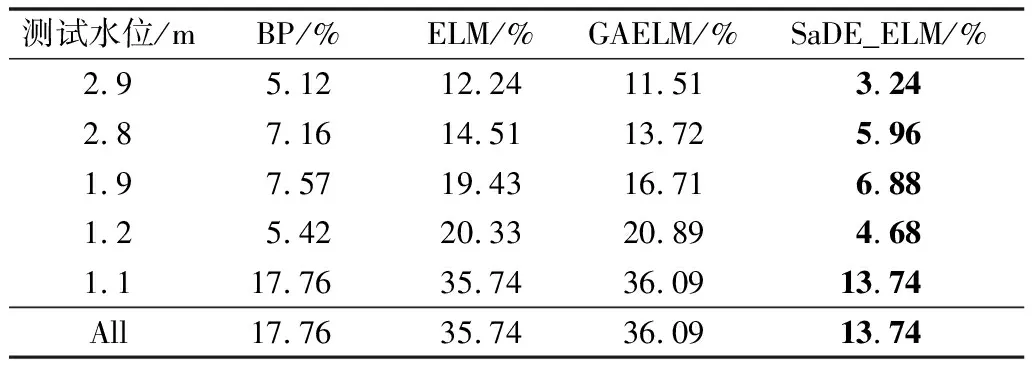
表4 不同模型的最大相对误差Tab.4 MAXE of different models
MAXE=max(|En|)n=1,2,3,…,N
(20)
分析表格结果可知,对于SaDE_ELM模型,其MARE为2.86%,RMSE为3.50%,均不超过5%;即使在相对极端的水力环境下,其最大误差也不会超过13.74%;综上所述,本文应用的SaDE_ELM模型在流速场预测的精度和稳定性上,表现优异。
4 结 论
(1) 本文CFD仿真方法的MARE均小于4%并且RMSE均小于5%,符合明渠测量统一标准,适用于宽浅明渠的仿真,具有较高的精度。
(2) 对于5种测试水位下的断面流速分布规律,实时预测模型(SaDE_ELM)的预测结果更符合明渠流速分布一般规律,有较好的泛化能力。
(3) 对于5种测试水位下的流速预测误差,实时预测模型(SaDE_ELM)的MARE为2.86%,RMSE为3.50%,极端情况下的MAXE为13.74%,预测结果具有较高的精度和稳定性。
本文所提出的明渠“水位-流速场”实时预测模型,不但预测的流速场符合流速分布的一般规律,而且能预测断面任意点的流速值,具有强泛化能力和高精度,对工程应用和理论研究具有较高参考价值。
