水泵水轮机内部流态特性及预应力模态分析

2023-09-25孔令华,姜爱军,李向阳,李思原,郭绘娟

人民长江 2023年9期

孔令华,姜爱军,李向阳,李思原,郭绘娟

(1.福建仙游抽水蓄能有限公司,福建莆田 351267; 2.河海大学水利水电学院,江苏南京 210098)

0 引言

“双碳”背景下抽水蓄能电站迎来巨大发展[1]。随着大型抽蓄机组的投运,水力激振所引起的稳定性问题日益突出[2-3],严重影响电站安全[4-6]。开展水泵水轮机压力脉动特性研究,不仅可以提高水电站运行稳定性和供电质量,还可以促进清洁能源高效利用和电网系统协调智能发展。李剑华等[7]对不同工况下无叶区压力脉动进行研究,得到了内部流场和压力脉动的关系。冯俊等[8]研究表明改善水泵水轮机内部压力脉动情况,对降低流动诱导噪声水平有着重要影响。李萍等[9]研究发现动静干涉对无叶区的压力脉动影响最大。桂中华等[10]将转轮固有模态与动静干涉理论相结合,从而对异常振动产生的原因进行分析,发现激励力的瞬变特性对转轮的振动影响在共振工况附近尤为明显。Lu等[11]发现在无叶区内顺时针运动的旋涡是导致流动分离的主要原因。Laouari等[12]发现在部分负荷和过载工况下,压力脉动和扭矩振动更为明显。Mauro等[13]检测到固定叶片和导向叶片之间存在强烈的流动相互作用,使得导叶叶片上的压力分布不规则。从目前较多的文献来看,大部分研究针对压力脉动进行简单分析,对于水泵水轮机的压力脉动传播机理以及转轮和活动导叶之间的动静干涉研究较少。其次,结构受到预应力的影响,会增加结构刚度,从而导致频率的变化,对预应力下水泵水轮机的模态分析较少,而模态又是分析水力激振与机组共振的重要途径。

本文通过ANSYS Workbench平台对大型水泵水轮机在不同水头工况下进行全流道数值计算,与试验结果进行对比以验证其可靠性,得到水泵水轮机过流面的水压力分布及压力脉动特性,进而得到预应力下水泵水轮机的模态特性,开展水泵水轮机共振可能性的分析,以期对水泵水轮机结构优化设计提供一定的参考。

1 水泵水轮机压力脉动分析

1.1 研究对象

以抽蓄电站中应用的水泵水轮机为研究对象,采用数值模拟对其不同水轮机工况进行流场分析。水泵水轮机全流道模型如图1所示。固定导叶数为20,活动导叶数为20,转轮叶片数为9,转轮高压侧直径为4 158 mm,低压侧直径为2 238 mm,额定转速为428.6 r/min,额定水头为430 m。

分析压力脉动是对机组内部流场进行研究的重要手段,为了得到不同工况下机组中各部件的压力脉动情况,以及同一过流部件周向压力脉动变化规律,沿水流流动方向依次在蜗壳、蜗壳与固定导叶交界面、固定导叶与活动导叶交界面、活动导叶与转轮交界面周向上均匀设置若干监测点,即点W14～W54,G14～G44,H13～H43,Z13～Z43。考虑到尾水管涡带旋转摆动的不确定性,在尾水管进口处以及距离尾水管进口1.9,3.5,5.6 m处设置4组监测点便于了解涡带发展情况,即C1,C2,C3,C4组;同时为了解导叶周围压力脉动情况,沿导叶周向均匀布置若干监测点,即点HA1～HA10,GA1～GA10;为了解转轮内部压力脉动情况,设置监测点ZH1～ZH12,如图2所示。

图2 监测点设置Fig.2 Setting of monitoring points

1.2 计算方法

边界条件设置为压力进、出口,旋转域与固定域交界面采用Frozen Rotor,采用SSTk-ω模型[14]进行数值计算,该模型在广泛的流动领域中有更高的精度和可信度。非定常计算中设置转轮转过3°的时间(1.17×10-3s)为一个步长,针对该水泵水轮机的复杂性,采用了自适应性较强的非结构化四面体网格以及边界层网格,并对固定导叶、活动导叶及转轮的叶片进行局部加密。经网格无关性验证,网格数为747万个,符合要求,各部件具体的网格划分情况如表1所列。

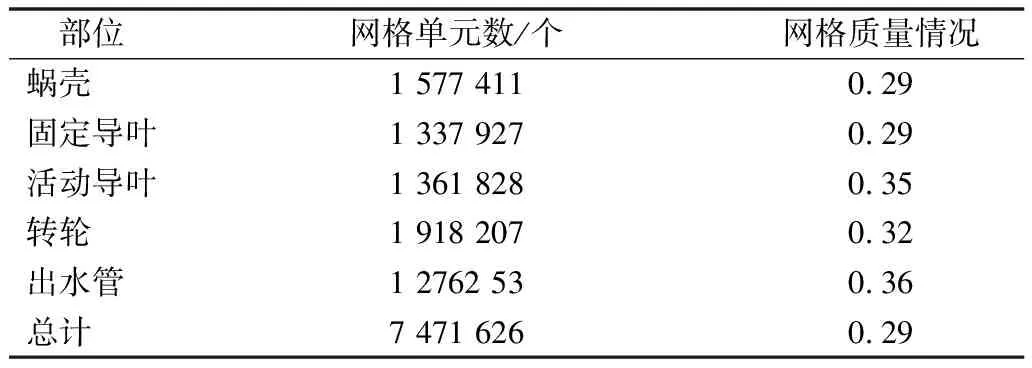
表1 网格单元数以及质量Tab.1 Number and quality of mesh elements

2 计算结果与分析

2.1 数值计算可靠性分析

为验证数值计算的可靠性,选取水泵水轮机在导叶开度为22°时的4个工况点(水头413,430,452,472 m)以及430 m水头下4个工况点(开度12°,21°,22°,30°)进行数值模拟,将数值模拟结果与现场试验结果进行对比。

试验在蜗壳进口压力区、无叶区压力区、顶盖压力区、尾水压力区布置英国DURCK压力传感器(测量范围0～70 MPa,精度±0.04%),在上导、下导、水导、上机架、定子机座、下机架、顶盖等设置机组振动与主轴摆度测点,共28点,见图3。单元控制柜得出有功功率,上、下游水位由人工读数。机组振动位移量、主轴摆度与压力脉动的混频幅值取值方法采用按97%置信度的混频峰峰幅值进行取值。

机组测点振动结果见图4。机组振动各测点主频主要为转频7.13 Hz、叶片过流频率(叶片数×转频=9×7.15=64.35 Hz)的2倍频率128.57 Hz。机组压力脉动主要频率成分有叶片过流频率及其倍频。尾水压力脉动的主频为3.9～4.2 Hz左右的尾水管涡带频率。

图4 机组测点振动结果Fig.4 Vibration results of monitoring points

通过换算得到单位流量Q11,绘制出开度与单位流量(α-Q11)、效率与单位流量(η-Q11)关系曲线,将数值计算与试验的结果进行对比,所得结果见图5。相对误差值为4.3%,在允许范围内(<5%),数值计算结果具有较高的吻合度,表明此计算所采用的网格、湍流模型及计算方法能够较好地预测水泵水轮机内的流体流动特性,验证了数值模拟的可靠性。

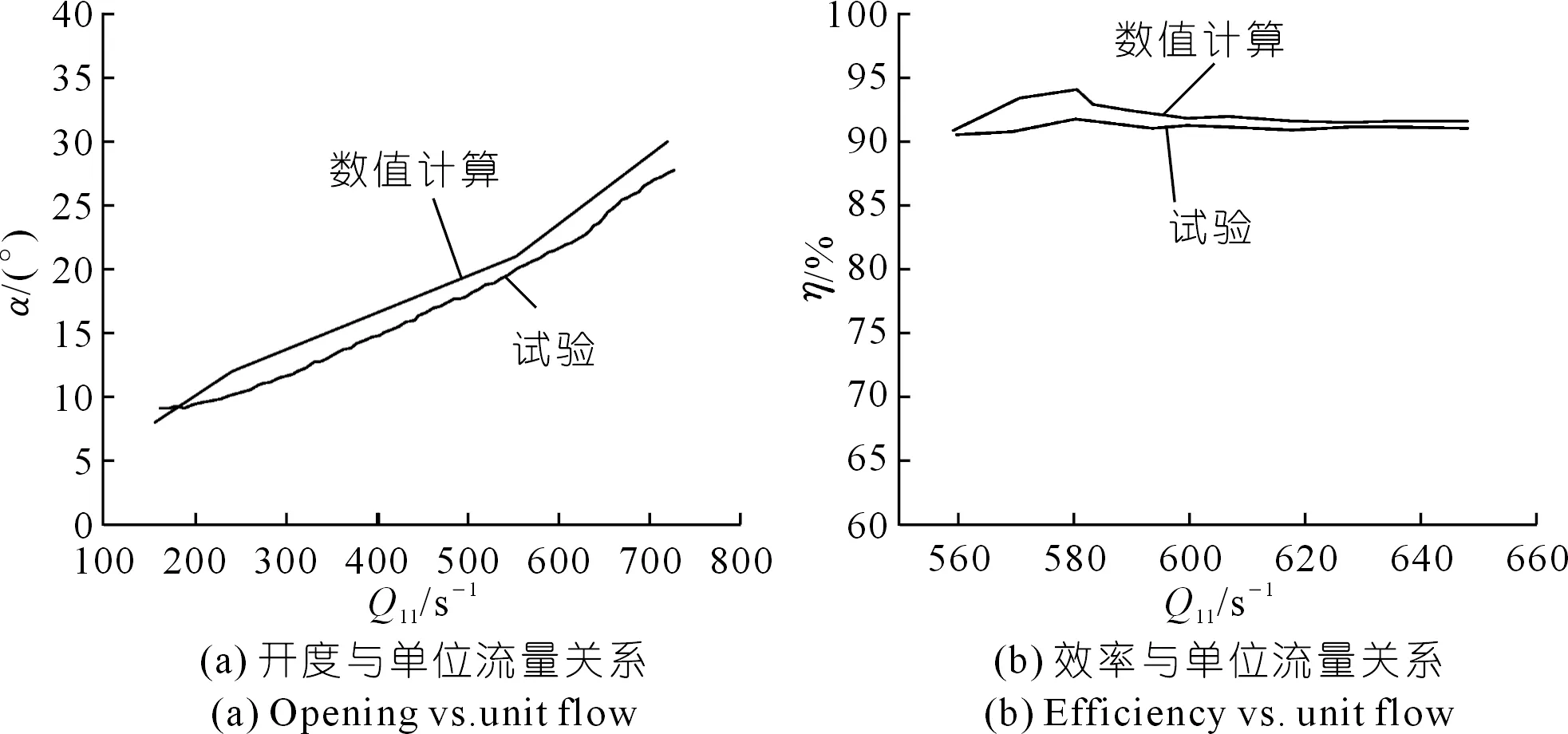
图5 试验与模拟结果对比Fig.5 Comparison of experimental and simulation results

2.2 定常结果分析

选取水泵水轮机4个工况点(活动导叶开度22°,工况1水头413 m,工况2水头430 m,工况3水头452 m,工况4水头472 m)进行稳态数值模拟,分析水泵水轮机在不同水轮机工况下所表现的内部典型区域流态分布特征。

2.2.1转轮叶片压力分析

图6为水泵水轮机的转轮叶片表面压力分布。转轮压力由叶片头部至尾部均有下降的趋势,压力面压力高于吸力面压力。活动导叶流出的水直接冲击转轮叶片吸力面入口段,导致出现明显的局部高压区。随着水沿流道继续流动,同时不断对转轮做功,消耗自身的能量,在出口处压力有所减小,压力分布均匀,状况良好。随着水头增大,叶片两侧压差增大,工况2下的压力变化线与进口和出口接近平行的程度较其他工况好,符合实际运行原理。

注:各分图中左图为压力面,右图为吸力面图6 叶片表面压力分布(单位:Pa)Fig.6 Pressure distribution on blade surface

2.2.2尾水管内部流动分析

图7、8是在4种工况下尾水管的静压分布和流线分布。水压力脉动与水流涡带现象联系密切[15]。尾水管直锥段较长,使得水流在转轮进口处有较大程度收缩,压力脉动将导致机组运行稳定性的问题,并造成较大的水力损失。尾水管性能的优劣对水泵水轮机的运行效率、空蚀特性和发电机组整体工作的稳定性等方面具有直接影响。

图7 尾水管内压力静压分布Fig.7 Static pressure distribution in tailpipe

以转轮中心为原点,在尾水管直锥段内即垂直方向上距离原点1,4,7 m处取三个截面,在尾水管扩散段即水平方向上距离原点4,8,16 m处取三个截面。可以看出,水轮机工况下尾水管内部流场的整体速度分布呈现出均匀的特点,图7中水流经转轮旋转后进入尾水管进口处,此处压力及速度分布基本对称,大范围的低压区却出现在中心位置。由于水流向后流动,图8中在尾水管的直锥段至弯管段之间,产生了与转轮旋转方向相同的偏心涡带。在高水头下,此特性尤为明显,涡带绕尾水管的轴心发生旋转,在尾水管上部涡带较大且流线混乱,中心处的压力明显低于涡带及其周围的压力。随着水流继续往前流动,流线变得略微平顺,工况2尾水管内流态较其他工况好。

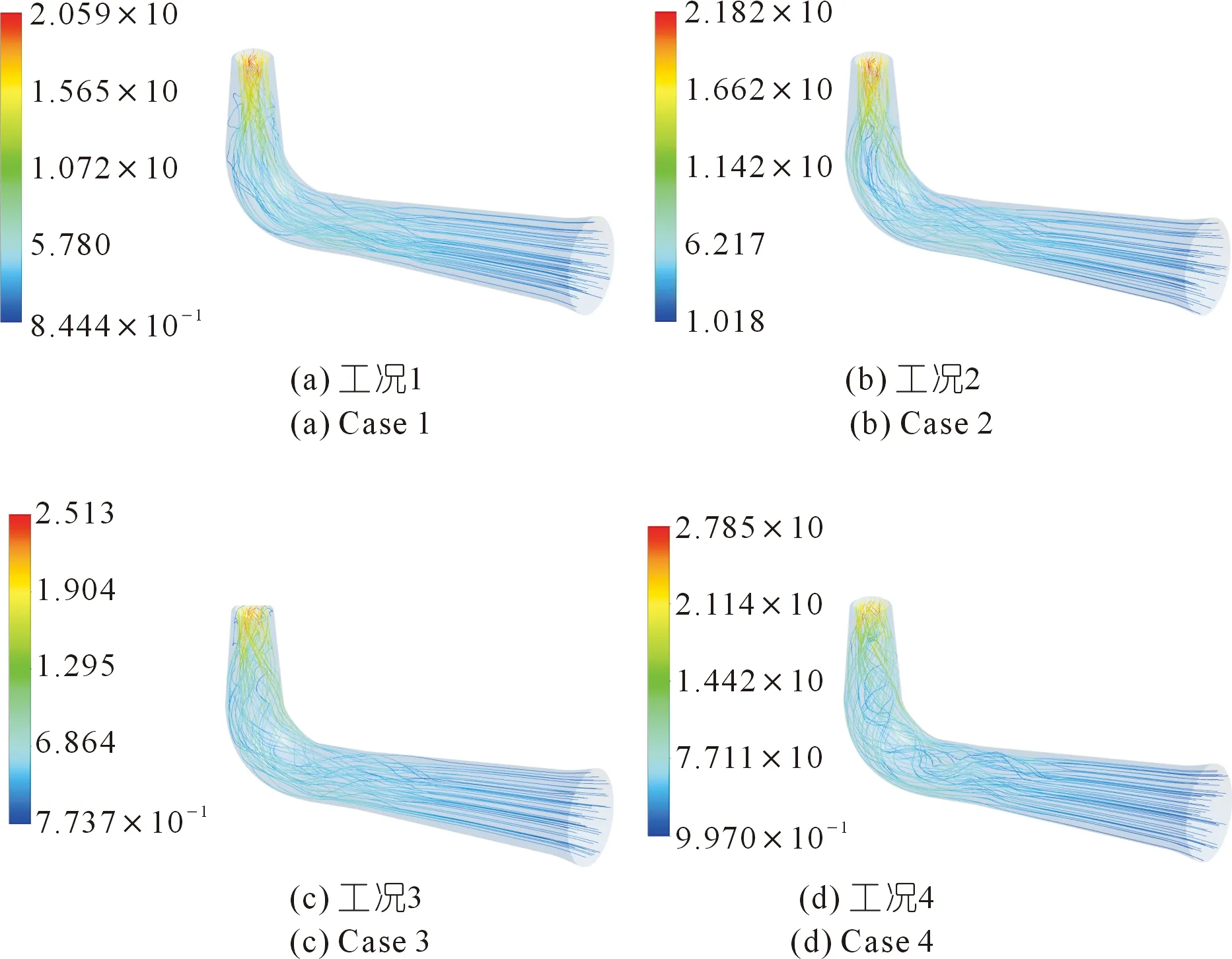
图8 尾水管内流线分布(单位:m/s)Fig.8 Streamline distribution in tailpipe

2.3 非定常结果分析

经过不同工况下非定常计算,发现压力脉动具有一定的相似性,考虑到本文主要研究压力传播规律,因此针对工况2进行分析。

2.3.1蜗壳压力脉动分析

图9为蜗壳压力脉动时域图与频域图。水流在蜗壳进口处的速度较小,流动也相对稳定,所以相比于其他部件的压力脉动振幅也较小。由频域图可知,主频为127.670 Hz,约为18倍转频,次频为63.840 Hz,约为9倍转频,即1倍叶频,蜗壳进口处的压力脉动频率主要是动静干涉传播所造成的。靠近固定导叶的监测点W54振幅最大,受动静干涉传播影响最大。

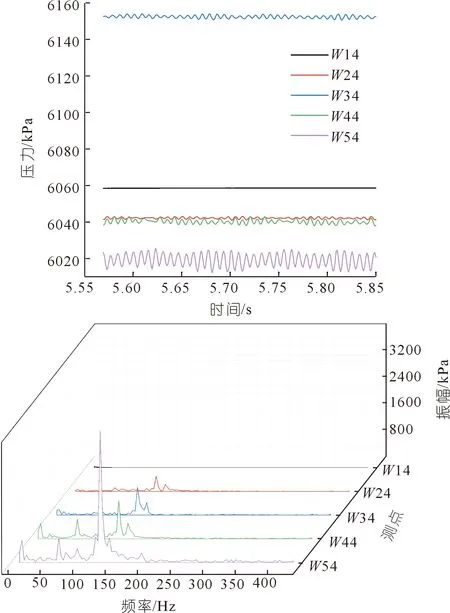
图9 蜗壳W14～W54压力脉动时域图与频域图Fig.9 Pressure pulsation time domain and frequency domain diagrams of volute W14～W54

2.3.2导水机构压力脉动分析

图10为固定导叶流道内各监测点压力脉动时域图与频域图。周向上时域图呈现出一定的相位差,GA1 监测点靠近固定导叶与蜗壳交界处压力波动幅度最小。随着监测点逐渐靠近转轮进口移动,GA5、GA6、GA7处转轮与活动导叶间动静干涉作用明显,其压力随时间的变化剧烈,固定导叶与蜗壳交界处的周向分布监测点主频为127.673 Hz(18倍转频),次频为63.836 Hz(9倍转频)。

图11为活动导叶流道内的压力脉动频域图。因为固定导叶的影响以及转轮对活动导叶有一定的激励,水轮机工况下导叶流道内的压力脉动主频均为63.836 Hz(9倍转频),为转轮叶片通过的频率,所以转轮与活动导叶间相互作用下的动静干涉是压力脉动的主要来源,随着压力脉动沿上游向活动导叶传播时,强度逐渐减弱;周向上,从时域图看出,存在一定的相位差,符合实际运行原理。此外,在固定导叶和活动导叶交界处,还存在着脉动幅值较大的127.673 Hz(18倍转频)频率成分,说明导水机构压力脉动频率成分以9倍转频和18倍转频为主,即叶片通过频率和2倍叶片通过频率。在活动导叶叶片周向的监测点,存在三阶次频191.509 Hz(27倍转频)。

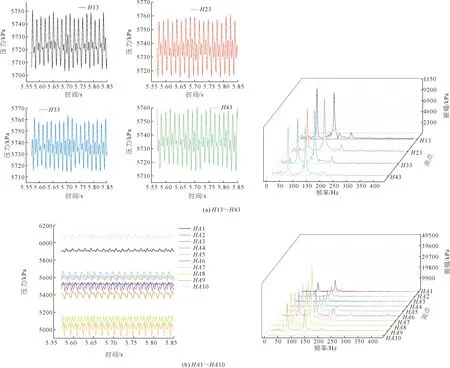
图11 活动导叶流道内的压力脉动时域图与频域图Fig.11 Time domain and frequency domain of pressure pulsation in the guide vane passage

2.3.3转轮流域压力脉动分析

图12为转轮流道内的压力脉动时域图与频域图。图中监测点压力脉动呈现良好的周期性。由频域特性可知,活动导叶与转轮的动静干涉起主要作用。位于活动导叶与转轮之间的无叶区的监测点Z23的压力波动幅度较大,主要是转轮与活动导叶间存在着较小的空间,导致转轮与活动导叶间的动静干涉作用增强,造成波动剧烈的压力波动在无叶区出现,所以转轮与活动导叶间相互作用下的动静干涉是压力脉动的主要来源,沿上游向活动导叶传播时,压力脉动强度逐渐减弱,与前文相吻合。此外,存在脉动幅值较大的 127.673 Hz(18倍转频)频率成分,说明转轮流域压力脉动频率成分以18倍转频为主,其次还存在63.836 Hz的次频,即叶片通过频率和2倍叶片通过频率。在活动导叶叶片周向的监测点,Z33测点存在三阶次频191.509 Hz(27倍转频)。

图12 转轮流道内各测点的压力脉动时域图与频域图Fig.12 Pressure pulsation in time domain and frequency domains at each measuring point in runner passage

2.3.4尾水管压力脉动特性分析

图13是尾水管监测点压力脉动时域图和频域图。从C1～C4组以看出,沿水流向下,受到转轮转动影响和尾水管涡带的影响权重不同。C1组靠近转轮出口,受转轮转动的影响,从频域图可以看出主频是63.84 Hz,C14测点的主频为7.09 Hz,可能是由尾水涡带引起的。C2组水流经直锥段进一步发展,主频为7.09 Hz,受尾水管涡带影响较大,次频为63.84,127.67 Hz,为叶频及两倍叶频。C3组受尾水管涡带影响较C2组更大,涡带在此充分发展,主频为7.09 Hz,次频为63.84,127.67 Hz,为叶频及两倍叶频。C4组在频域图上和C3组保持一致,与试验结果存在一些误差,主要因为存在较多低频,信号叠加现象发生在不同频率的涡之间,造成压力脉动的频率、振幅等发生相应改变。

图13 尾水管流道内各监测点的压力脉动频域图Fig.13 Frequency domains diagram of pressure pulsation at each monitoring point in tailpipe passage

2.4 水泵水轮机预应力模态分析

自振频率是物体结构自身的固有属性,研究物体的自振频率对于避免物体结构由于其他振动而引起的共振进而造成的结构破坏具有非常重要的意义。水泵水轮机在工作过程中,其转动会对水流产生一个作用力,水流的作用力又会反作用于水泵水轮机,而水泵水轮机受水力的作用,自身的振动频率可能会发生改变,通过计算水泵水轮机在预应力作用下的模态受影响程度,对水轮机组的稳定安全运行具有非常重要的意义。

在结构有限元计算中,能否正确给出结构的边界条件是保证有限元计算准确的关键[16-18]。本文根据机组运行的实际情况确定了水泵水轮机的边界条件,即:① 考虑水泵水轮机与上端轴通过螺栓连接的实际情况,需要限定水泵水轮机在X,Y,Z三个方向的运动,即对水泵水轮机的上冠位置予以固定约束;② 考虑水泵水轮机实际运行状况,在空间上设置重力加速度和旋转角速度的边界条件;③ 在水轮机的工作过程中,水流在叶片表面产生作用力,通过应力模块将流体计算结果中所获得的叶片表面压力施加到水泵水轮机的叶片上,如图14(a)所示,叶片水压力加载见图14(b)。结构场计算中,网格采用mesh模块进行划分,经网格无关性验证后网格尺度选择为20 mm。

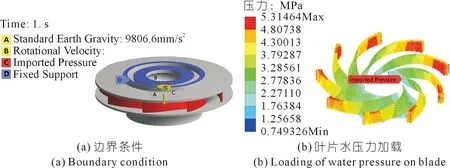
图14 结构计算边界条件Fig.14 Boundary condition of structural analysis

在静应力计算的基础上,对水泵水轮机进行模态分析就可以得到水泵水轮机的预应力模态。应力刚化是指构件在无应力状态和有应力状态下的刚度变化。在有应力状态下,构件某方向的刚度显著增大,导致结构的固有频率产生变化。表2即为水泵水轮机预应力下的模态,可以看出不同水头下预应力模态差别较小,不会发生应力刚化效应。

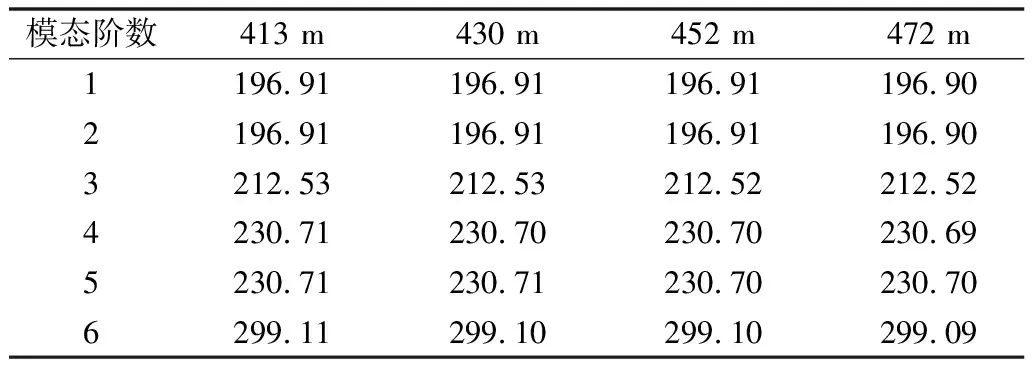
表2 不同水头下水泵水轮机预应力模态Tab.2 Prestressed mode of pump turbine Hz

图15为水泵水轮机的预应力模态分别对应的振型图。从中可以看出,转轮叶片1、2阶振型以及4、5阶振型基本相似,但旋转了40°,在求解叶轮模态的时候,叶轮结构共9片叶片,呈对称结构,因此在求解的结果中出现了重根的情况。水泵水轮机1阶、2阶振型主要表现为上冠、下环及叶片的扭曲变形及前后摆动,并且振动趋势为沿轮毂到轮缘逐渐增大;3阶振型表现为沿Z向上下摆动;4阶、5阶和6阶振型表现为叶片轮缘处对称的交错摆动。