考虑随机横向节理的反倾层状边坡倾倒破坏分析
2023-09-25屈新,王世新,徐兴倩,陈上元
屈 新,王 世 新,徐 兴 倩,陈 上 元
(1.安阳工学院 土木与建筑工程学院,河南 安阳 455000; 2.云南农业大学 水利学院,云南 昆明 650201)
0 引 言
倾倒破坏是层状岩体边坡常见的一种破坏模式,在自然边坡和工程边坡中均有发生,其中在反倾向层状边坡中最为常见[1-2]。尽管天然条件下反倾向边坡稳定性较好,但是在降雨、坡脚开挖、地震等外在因素作用下,岩层会发生弯曲倾倒变形,并逐渐向坡体内部发展、延伸,形成折断面,进而形成滑坡[3]。频繁发生的反倾向层状边坡失稳事故不仅严重影响工程建设,而且对人们的正常生活和生命财产安全构成威胁。
为了解决这类工程问题,大量学者对反倾向层状边坡的稳定性问题开展了研究,并在其地理分布特征、岩体结构特征、发育规模、发育条件、变形演化过程、变形机制及稳定性评价等方面取得了研究成果[4-11]。这些研究表明,节理裂隙的发育程度对反倾向层状边坡的倾倒失稳破坏起着决定性作用[12-17]。Majdi等[12]认为当裂隙长度小于临界值时,若改变裂隙长度,稳定系数变化不大,但改变裂隙连通率,稳定系数数值变化很大;当裂隙长度超过临界值时,改变裂隙长度和裂隙连通率对稳定系数影响都很大。Zhao等[13]考虑了节理间距不均匀对弯曲刚度的影响,并建立了基于变形协调的抗弯倾倒破坏模型。该模型将边坡划分为自由变形区和相容变形区,各个岩层的安全系数由弯矩计算得出,其中最小系数则代表整个边坡的安全系数,此外,他们建议采用平均刚度法建立等厚反倾向边坡模型。杨磊[14]利用赤平投影法、Bishop法和Mogenstern-Price法分析了考虑和不考虑岩体节理的边坡稳定性,并制定了不稳定边坡的工程治理方案和防护措施。唐晖等[15]探讨了高陡岩质边坡安全系数与裂隙产状之间的关系,分析了节理倾角、倾角分散趋势、倾向、倾向分散趋势对边坡安全系数的影响。张宜杰等[16]结合现场调查,建立了有限元节理网络模型,同时结合Rosenbluth点估计法考虑了岩体强度参数的变异性,计算了边坡的稳定系数。Su等[17]基于等效弱化原则,建立了考虑节理裂隙的反倾向层状边坡模型,探讨了节理长度对边坡稳定性的影响,并发现随着节理长度的增加,边坡稳定性降低,边坡更容易发生浅层破坏。
上述研究大大完善了反倾向层状边坡弯曲倾倒破坏的理论基础,并初步揭示了规则节理对反倾向边坡倾倒破坏的影响规律,但鲜有考虑节理的随机特性。实际边坡工程中,横向节理的发育程度是反倾向层状边坡倾倒失稳破坏的一个重要因素,且节理位置分布随机、节理长度也各不相同,随机横向节理对反倾向边坡倾倒破坏的影响规律尚未完全清楚。为解决上述问题,本文通过计算机随机生成横向节理的位置系数和长度系数来表征横向节理的随机特性,建立随机横向节理反倾向层状边坡模型,探讨此类边坡发生倾倒破坏的启动条件,揭示边坡的破坏机理,并以一处反倾向层状板岩边坡为研究对象,阐明随机横向节理对反倾向层状边坡倾倒破坏的影响规律。
1 考虑随机横向节理的反倾向层状边坡模型
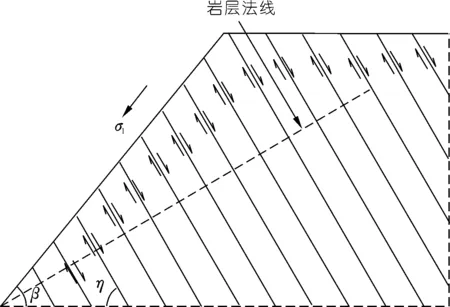
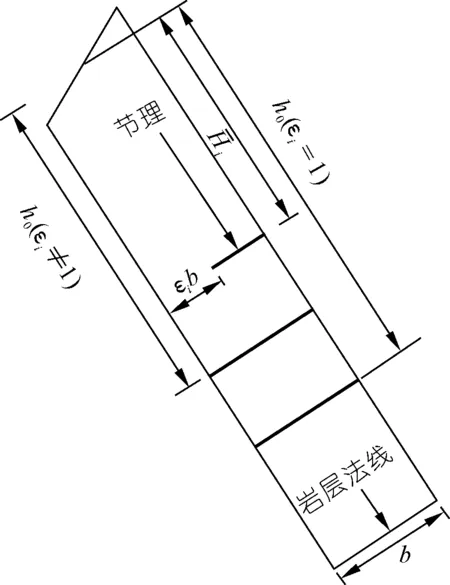
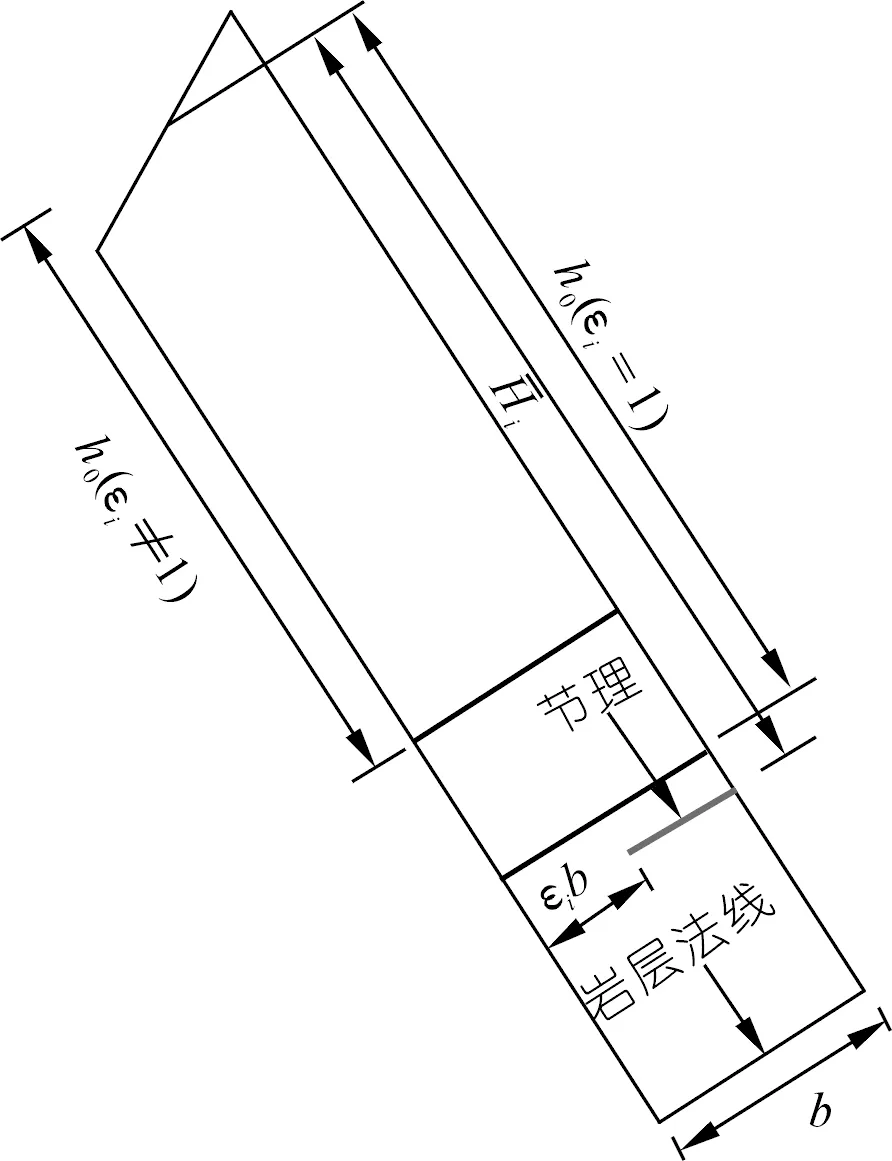
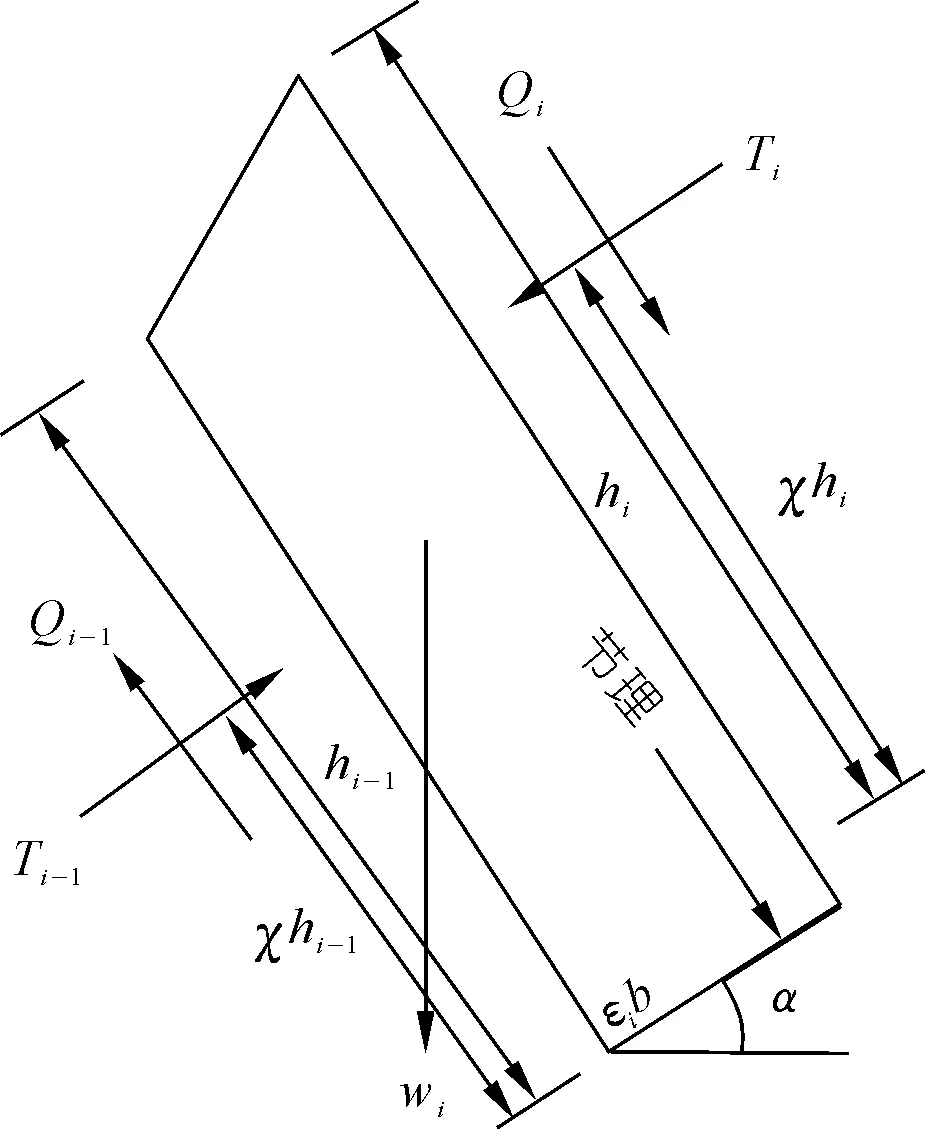
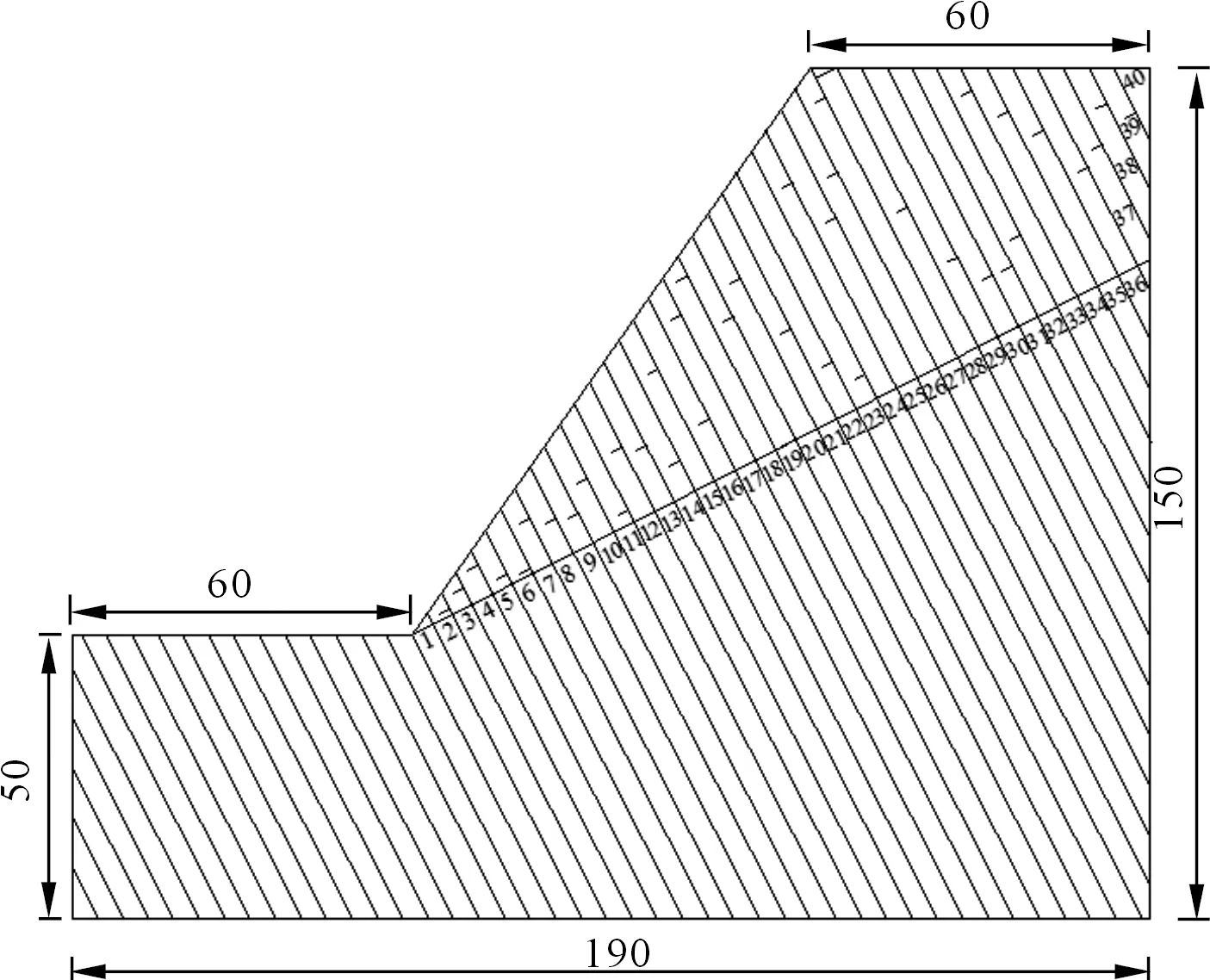
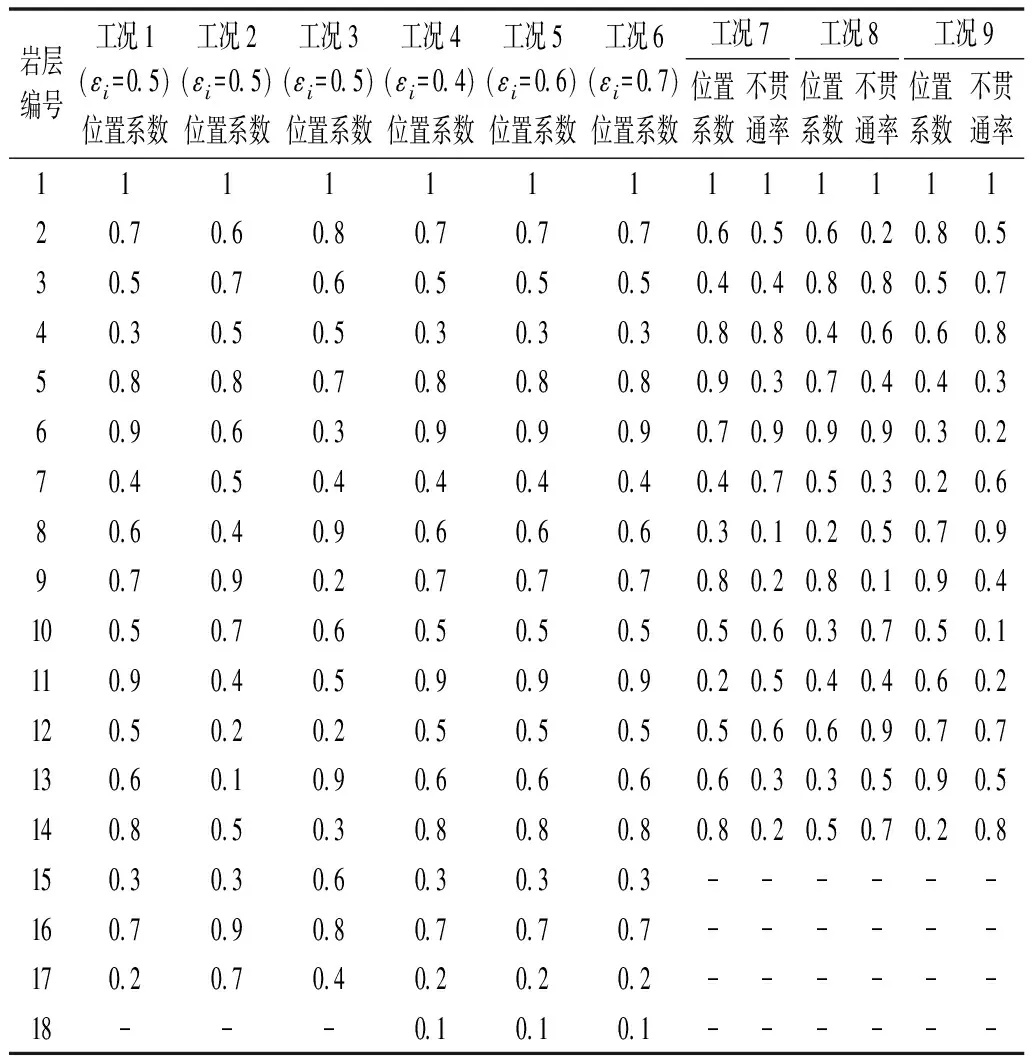
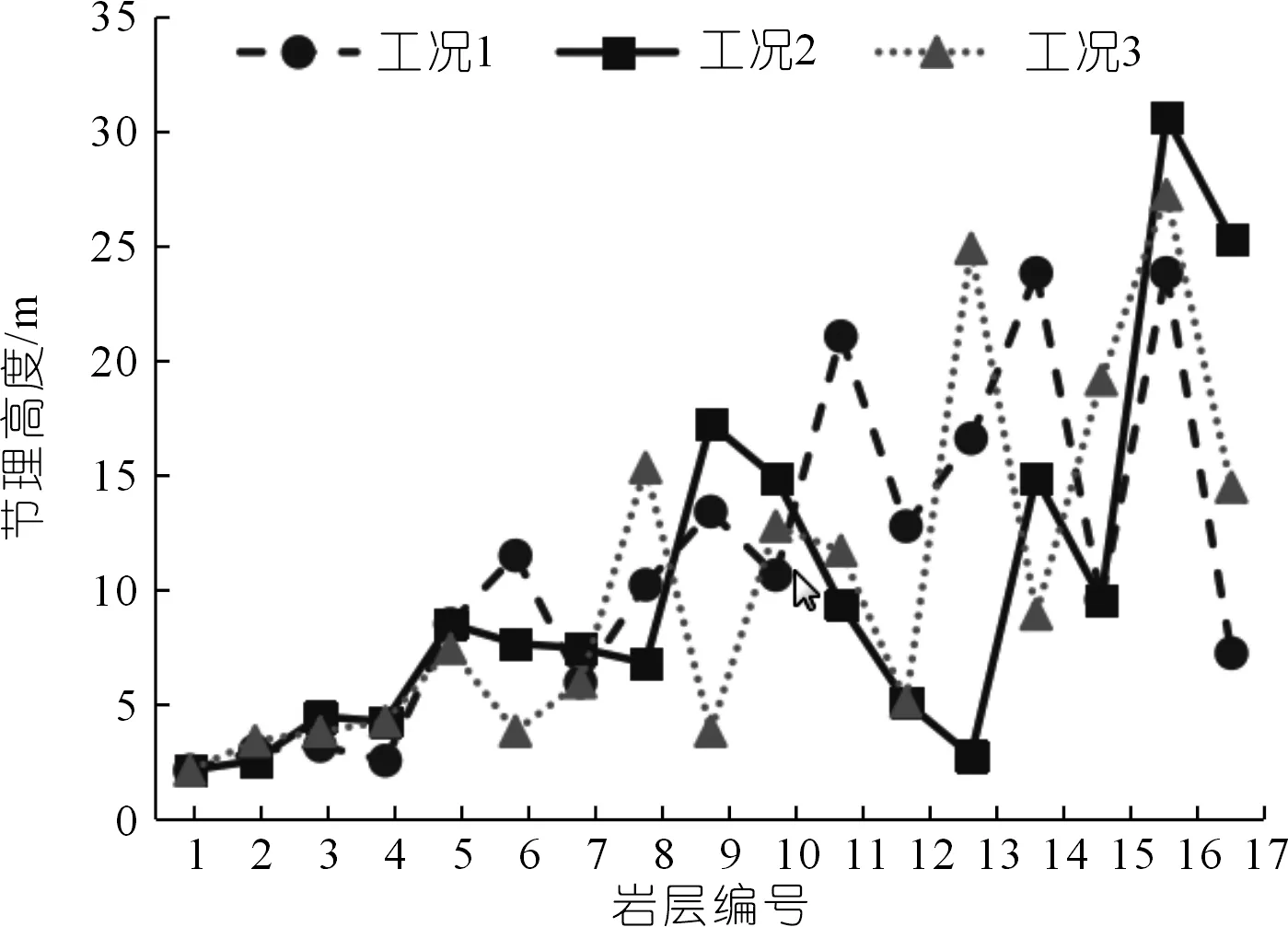
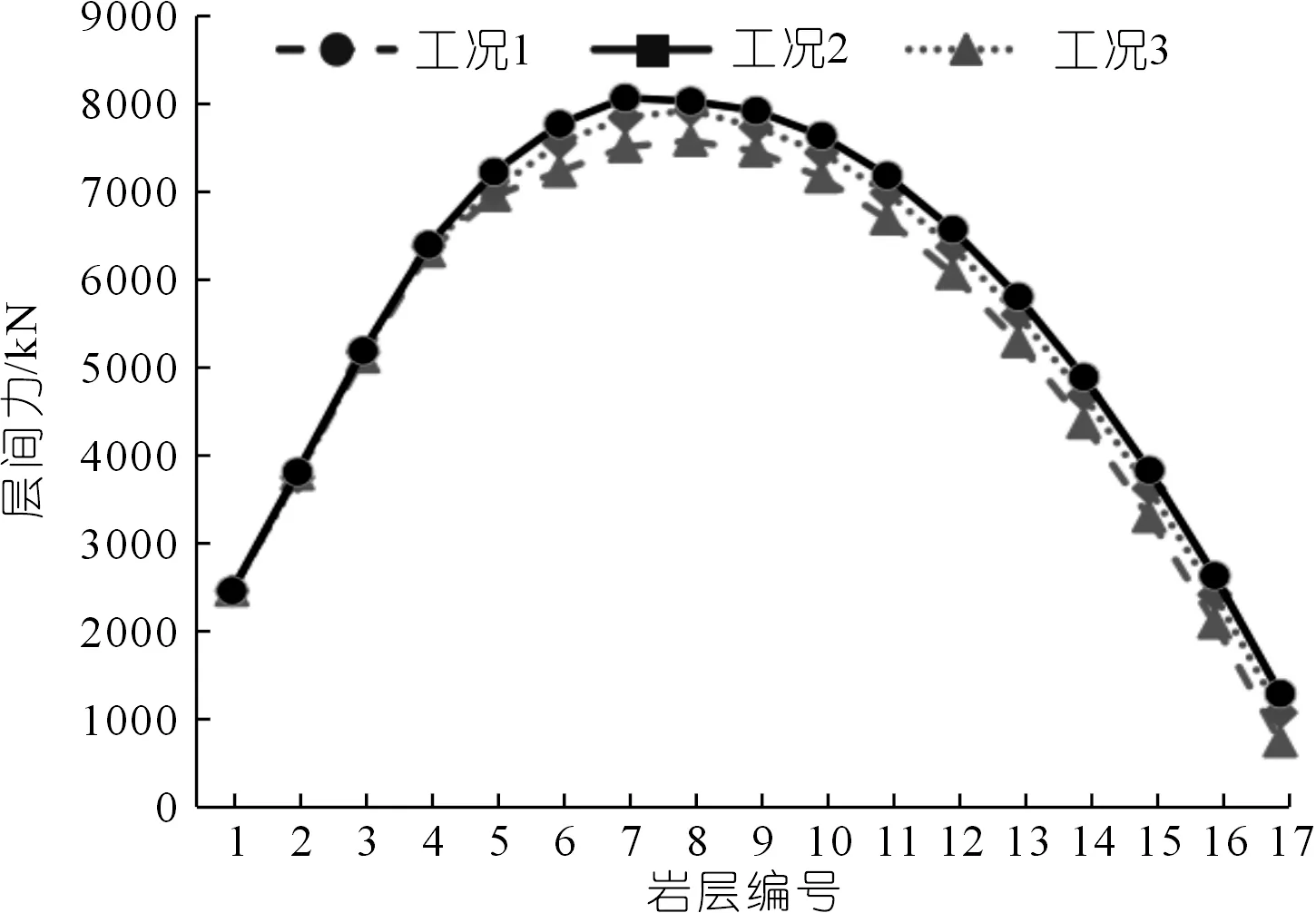
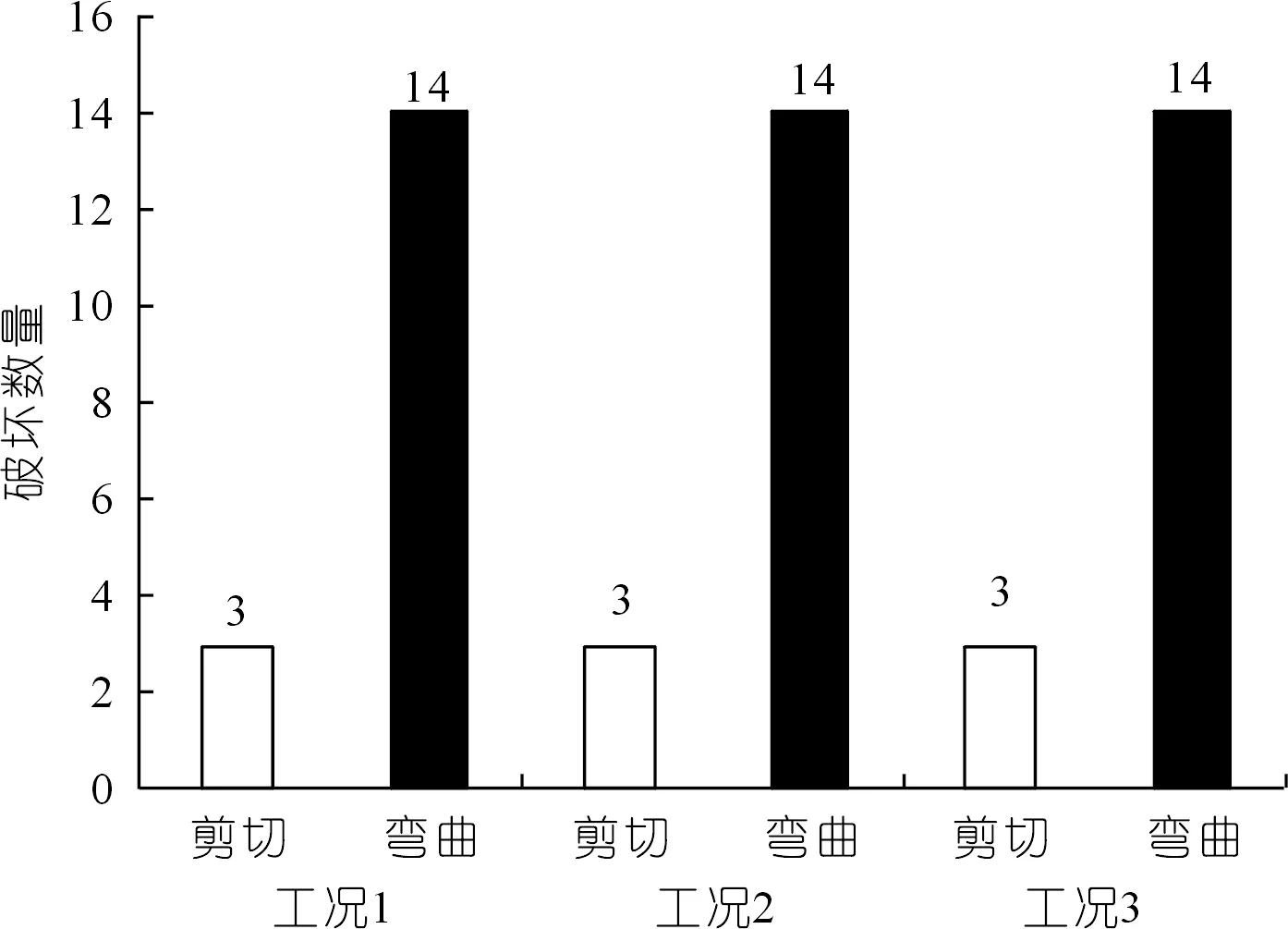
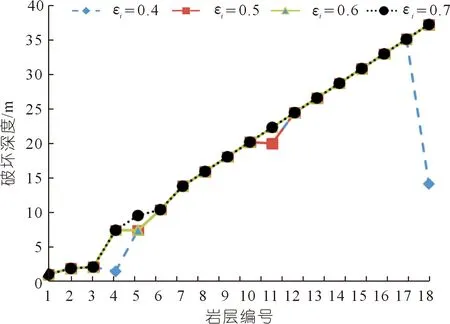
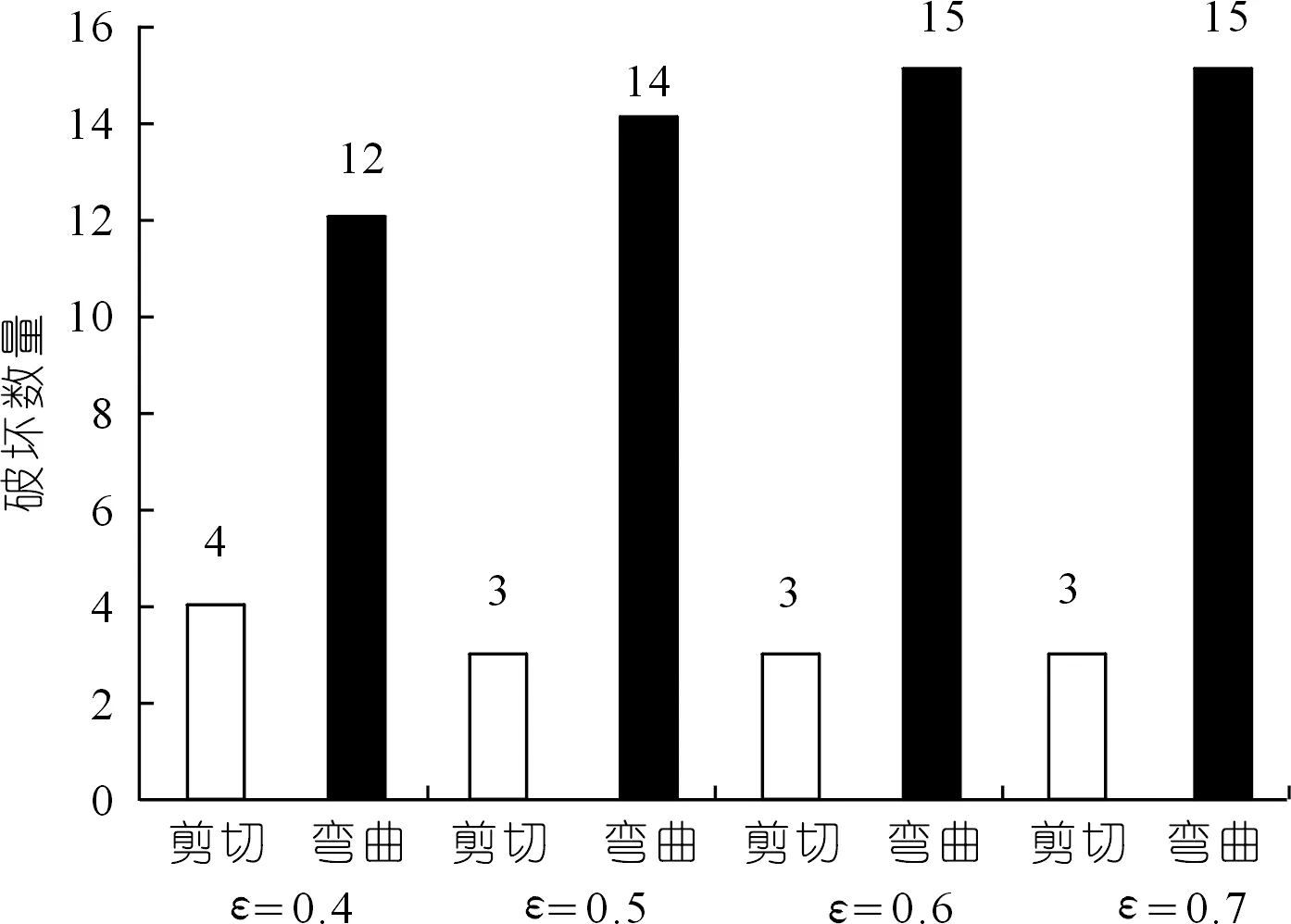
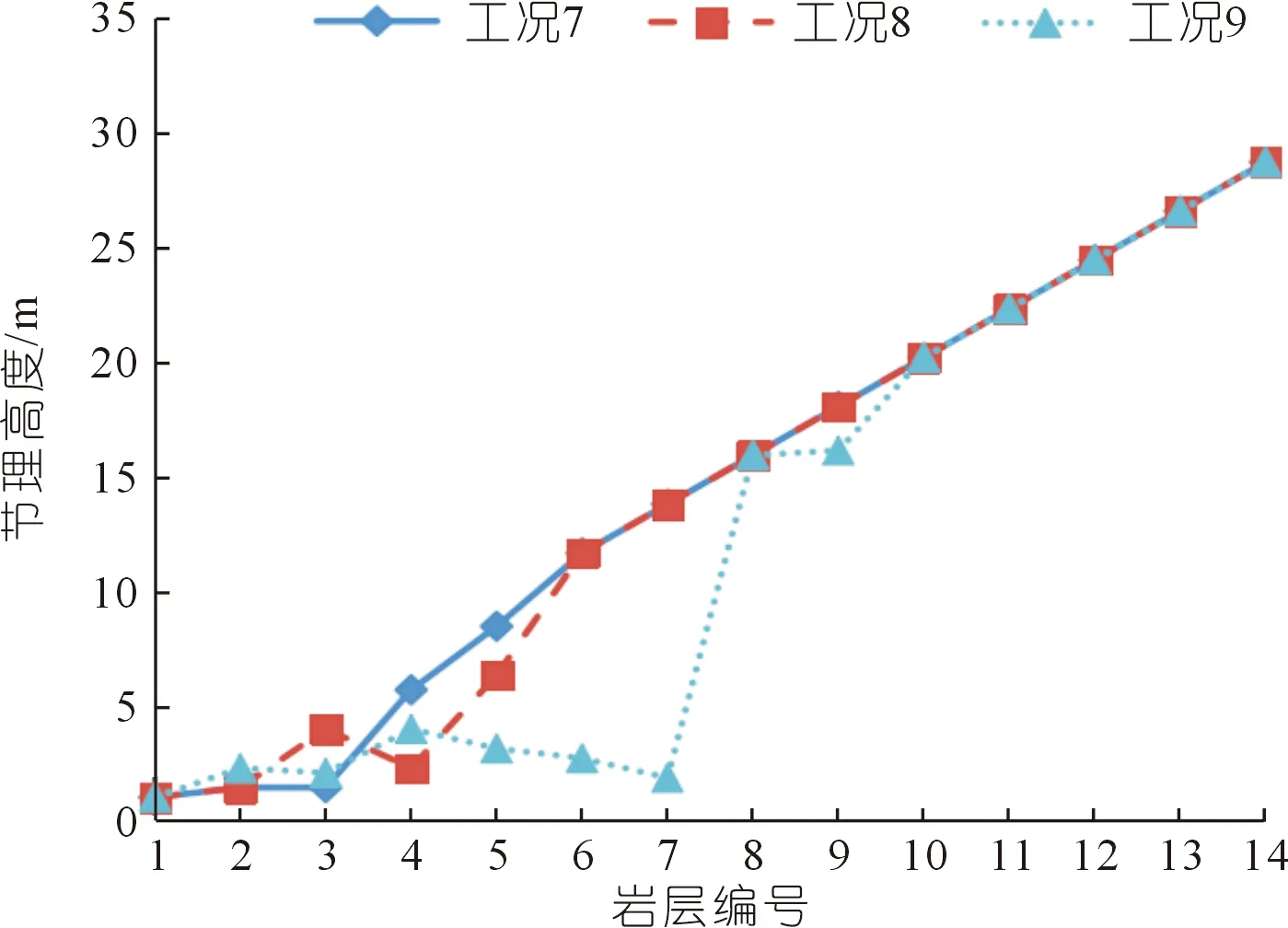
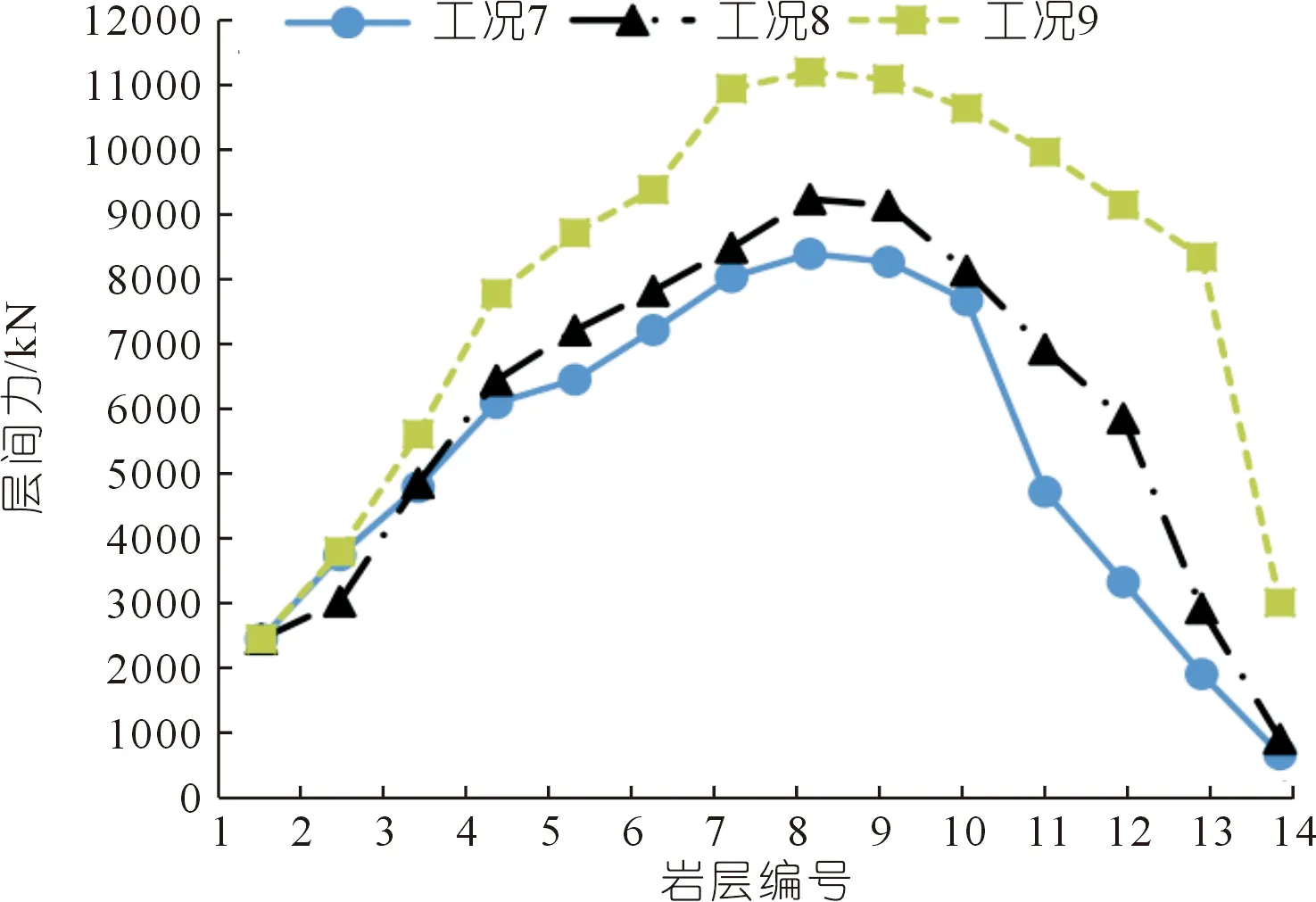
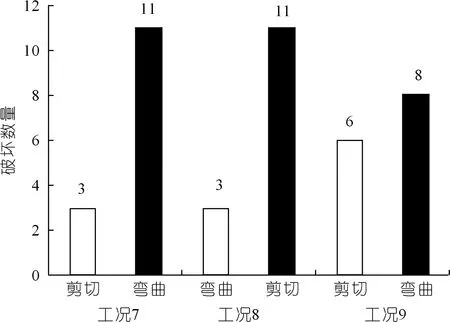
在反倾向层状边坡中,位于岩层法线(图1中黑色粗线)上部的部分为潜在不稳定区域,故本文只研究此部分岩层的力学行为。并在每个岩层顺坡向底部位置设置一条随机横向节理(图1中红色粗线),其方向与岩层层面垂直,其长度为(1-εi)b,则岩层i底部未贯通长度为εib。其中εi为岩层i底部的节理不贯通率,它等于未贯通岩层长度与完整岩层底部长度(厚度)的比值。坡脚处岩层的不贯通率εi等于1。通过计算机随机生成节理长度系数(节理不贯通率)εi(0<εi≤1)和节理位置系数K(0 图1 随机横向节理反倾向层状边坡模型Fig.1 Model of anti-dip stratified slope with random cross joints 基于反倾向层状边坡倾倒破坏方面的研究结论[10-11,17-19],采用以下几条假设来简化倾倒破坏的分析过程:① 临界破坏状态时,所有潜在破坏岩层沿潜在破坏面处于极限平衡状态;② 以岩层为基本单元,层间作用力简化为集中力,作用点位于χhi处,hi为岩层i与岩层i+1的接触长度,χ为推力线高度(0<χ≤1),本文取0.5。 斜坡的变形与破坏主要取决于坡体的应力分布特征和岩土体的强度特性。其中,坡体应力分布主要受坡面几何形态的影响,而岩土体强度主要受控于岩层结构面特性。对于反倾向层状边坡,坡面几何形态的主要要素是坡角和岩层倾角。层面强度(层面内摩擦角)直接决定着岩层间相互滑移的难易程度,是岩质反倾向层状边坡发生弯曲倾倒破坏的前提条件[20]。综上,反倾向层状边坡发生弯曲倾倒破坏时,岩层倾角、边坡倾角与层面内摩擦角必须满足一定的关系,可通过如下推导得出。 斜坡开挖形成反倾向层状边坡后,坡面附近的最大主应力σ1近似平行于坡面(如图2所示),最小主应力σ3(忽略)近似与坡面正交,第二主应力σ2为0,则岩层发生错动的下滑力和抗滑力都由σ1提供。将最大主应力σ1沿层面错动方向分解,可得下滑力为σ1sin[β-(90°-η)];将σ1沿岩层法线方向分解,可得层间法向接触力为σ1cos[β-(90°-η)]。基于库伦摩擦定理可知,层间摩擦力(抗滑力)为σ1cos[β-(90°-η)]tanφi(φi为岩层i层面内摩擦角)。当岩层i发生错动,则必定满足: 图2 反倾向层状边坡主应力分布Fig.2 Principal stress distribution of anti-dip layered slope σ1sin[β-(90°-η)]>σ1cos[β-(90°-η)]tanφi (1) 将式(1)左右两端同时除以σ1cos[β-(90°-η)],并进行整理可得,tan[β-(90°-η)]> tanφi,即, β-(90°-η)>φi (2) 只有当岩层倾角、边坡倾角与层面内摩擦角满足式(2)时,岩层才可能发生弯曲倾倒破坏。安晓凡[21]、谢良甫[22]、Qu[23]等分别从案例统计、数值模拟和理论分析的角度证实了这一结论。 需要注意的是,公式(1)并没有考虑层间黏聚力。因此,公式(2)只适用于不考虑层间黏聚力的情形。蔡俊超[24]建议采用综合内摩擦角来分析考虑层间黏聚力的层间错动启动条件。 层间错动停止之后,中上部岩层(坡肩)开始发生弯曲变形,坡脚处岩层由于变形空间受限,形成剧烈(剪切)挤压,并产生应力集中现象。随着弯曲变形的持续增加,坡脚处岩层的应力集中效应显著增大;当其剪应力超过岩层的抗剪强度时,坡脚岩层将剪断岩桥,形成剪出口,并为中上部岩层提供变形空间。中上部岩层长细比较大,抗倾倒能力较差,基本上都会发生弯曲倾倒变形。当其弯曲应力超过岩层的抗拉强度时,岩层将(弯)折断岩桥。综上,反倾向层状节理边坡的破坏应该是自有结构面拉裂或剪断岩桥导致破坏面贯通,直至破坏的全过程。 研究表明,节理岩体易沿着节理裂隙发生剪切或者拉裂破坏[17-19]。但理论分析显示,仅当节理裂隙发育在特定区域时,岩体才会在节理处破坏,否则岩体会在其他位置发生破坏。本文将节理岩体的破坏位置简化为3处:横向节理处、自重极限高度处(自重极限高度是指岩层在自重作用下在非横向节理处发生破坏的极限高度),以及岩层法线处。岩层的破坏应理解为岩层在自重极限高度处或者横向节理处或者岩层法线处萌生(扩展)裂纹,直到贯通整个岩层底面。节理岩体的破坏位置可按如下方法确定。 如图3所示,当横向节理位于节理极限高度上方时(节理极限高度是指岩层在自重作用下沿横向节理位置发生破坏的极限高度),岩层在横向节理处不会发生破坏。若岩层法线上部高度小于极限高度,则岩层也不会沿其法线位置发生破坏。此时,需要比较岩层在横向节理和法线发生破坏时所需外力,两者当中数值较小的对应的破坏位置即为岩层最可能发生破坏的位置。若岩层法线上部高度大于自重极限高度,则岩层将在自重极限高度处发生破坏。 图3 横向节理位于节理极限高度上方Fig.3 Cross joint above critical height of the joint 如图4所示,当横向节理位于节理极限高度下方、自重极限高度上方时,岩层将在横向节理处发生破坏。 图4 横向节理位于节理极限高度下方、自重极限高度上方Fig.4 Cross joint below the joint critical height and above the weight critical height 如图5所示,当横向节理位于自重极限高度下方,并且岩层法线上部高度大于极限高度时,则岩层将在自重极限高度处发生破坏。 图5 横向节理位于自重极限高度下方Fig.5 Cross joint below the weight critical height 当岩层位于潜在破坏面上部的高度大于自重极限高度时,就有可能发生破坏。自重作用下,岩层发生弯曲倾倒破坏的极限高度[17]为 (3) 由公式(3)可以确定潜在破坏区域,而该区域内所有岩层的破坏模式将通过如下分析确定。 如图6所示,若岩层i沿岩桥(横向节理)发生剪切破坏,则未贯通部分满足摩尔-库伦准则[17-20],即 图6 岩层i发生剪切破坏的受力分析Fig.6 Force analysis of stratum i occurring shear failure τ=σtanφ+c (4) 式中:τ为切应力,σ为正应力,φ为岩层的内摩擦角,c为黏聚力。 岩层i的贯通部分(横向节理)满足库仑摩擦定律。联立式(4),并结合岩层i的受力分析图,可得 (5) 式中:Pi为岩层i受到上部岩层的法向推力;Pi-1为岩层i受到下部岩层的法向推力;wi为位于破坏面上部的岩层i重力。式(5)中,当εi=1,即表示岩层i在非横向节理处发生剪切破坏时受到上部岩层的法向推力。 如图7所示,若岩层i沿岩桥(横向节理)发生弯曲拉裂破坏,则未贯通部分满足最大拉应力理论[10-11],即 图7 岩层i发生弯曲拉裂破坏的受力分析Fig.7 Force analysis of stratum i occurring flexural tension failure σmax=σt (6) (7) 式中:σt为岩层i的抗拉强度,Mi为岩层i底部未贯通部分的弯矩,Ni为岩层i的轴力。 联立公式(6)和(7),并结合岩层i的受力分析图,可得 (8) 式中:Ti为岩层i受到的上部岩层法向推力;Ti-1为岩层i受到的下部岩层法向推力;hi-1为岩层i与岩层i-1的接触长度;¯hi-1为岩层i破坏面以上的等效重心高度。式中,当εi=1,即表示岩层i在非横向节理处发生弯曲拉裂破坏时受到上部岩层的法向推力。 对于岩层i,若Pi 选取皖南山区典型反倾向板岩边坡作为本文的工程实例,研究随机横向节理对反倾向层状边坡倾倒破坏的影响。根据文献[25],边坡的计算参数如表1所列,从坡脚至坡顶对岩层进行编号,并布置随机横向节理,反倾向板岩边坡示意如图8所示。 表1 皖南板岩边坡计算参数Tab.1 Calculation parameters of slate slope in South Anhui Province 图8 皖南反倾向板岩边坡示意(尺寸单位:m)Fig.8 Schematic diagram of slate slope in South Anhui Province 横向节理长度保持不变,不贯通率εi取0.5。通过计算机随机生成3组位置随机数K,分别对应工况1、2、3,如表2所列。3种工况条件下,岩层的横向节理高度、破坏位置(即破坏深度)、层间作用力和破坏模式如图9~12所示,并可以得出以下结论: 表2 计算机随机生成的位置系数和长度系数Tab.2 Joint position coefficient and length coefficient randomly generated by computer 图9 工况1、2、3条件下1~17号岩层的横向节理高度Fig.9 The height of cross joints in rock strata 1~17 under working conditions 1,2 and 3 图10 工况下1、2、3条件下1~17号岩层的破坏深度Fig.10 Failure depth of rock strata 1~17 under working conditions 1,2 and 3 图11 工况1、2、3条件下1~17号岩层的层间力Fig.11 Interlayer forces of rock strata 1~17 under working conditions 1,2 and 3 图12 工况1、2、3条件下1~17号岩层的破坏模式及相应数量Fig.12 Failure modes and its numbers of rock strata 1~17 under working conditions 1,2 and 3 (1) 3种工况条件下,横向节理位置变化很大,但是1~17号岩层的层间作用力总是先增大后减小,变化趋势保持一致。 (2) 对同一个岩层(1~17号岩层)而言,随着横向节理位置的变化,层间作用力的大小也随之发生变化,但是变化幅度较小。横向节理位置的变化对坡脚区岩层的破坏位置的影响显著,但对中上部岩层的破坏位置的影响不大。 (3) 3种工况条件下,1~17号岩层的破坏模式完全一致,且破坏分区特性明显:坡脚区域的岩层发生剪切破坏,中上部岩层发生弯曲拉裂破坏。进一步证明了岩层的破坏模式与长细比的密切相关性。 (4) 3种工况条件下,岩层的破坏位置整体相差不大,但是坡脚区岩层的破坏位置差别较大。此外,当横向节理位置逐步向坡体深部移动时,岩层发生破坏所需的层间力明显增大,破坏位置也逐渐向坡体深部转移。 横向节理位置不变,横向节理位置随机数K取3.1节工况1对应的数值。考虑4种工况,横向节理不贯通率εi分别为0.5、0.4、0.6、0.7,分别对应工况1、4、5、6,如表2所列。4种工况条件下,岩层的破坏位置、层间作用力和岩层破坏模式如图13~15所示,可以得出以下结论。 图13 工况1、4、5、6条件下1~18号岩层的破坏深度Fig.13 Failure depth of rock strata 1~18 under working conditions 1,4,5 and 6 图14 工况1、4、5、6条件下1~18号岩层的层间力Fig.14 Interlayer forces of rock strata 1~18 under working conditions 1,4,5 and 6 图15 工况1、4、5、6条件下1~18号岩层的破坏模式及相应数量Fig.15 Failure modes of rock strata 1~18 under working conditions 1,4,5 and 6 (1) 4种工况条件下,横向节理长度变化较大,但是1~18号岩层的层间作用力总是先增大后减小,变化趋势保持一致。 (2) 对同一个岩层(1~18号岩层)而言,横向节理位置不变时,随着横向节理长度的减小(不贯通率增加),破坏时需要的层间作用力也随之增大,这与工程实际相吻合。并且层间力的大小随着横向节理长度不同的变化幅度较大,说明横向节理长度对岩层倾倒破坏的影响较为明显。 (3) 4种工况条件下,1~18号岩层的破坏模式基本上完全一致,且破坏分区特性明显:发生剪切破坏的岩层集中在坡脚区,发生弯曲拉裂破坏的岩层集中在中上部。 (4) 随着不贯通率的增大,岩层的破坏位置逐步向坡体更深的位置发展,岩层孕育破坏时间变长,说明边坡变得愈发稳定。但是,岩层发生破坏时所需的层间力变小、岩层孕育破坏深度增加,说明一旦边坡形成贯通的破坏面将发生更大规模的滑坡。 实际边坡工程中,横向节理的位置分布随机,长度也各不相同,二者共同决定着反倾向层状边坡的倾倒破坏。本节研究横向节理位置和节理长度同时改变对边坡倾倒破坏的影响。通过计算机随机生成3组位置系数K和节理不贯通率εi,分别对应工况7、8、9,如表2所列。3种工况条件下,岩层的破坏位置、层间作用力和岩层破坏模式如图16~18所示,并可以得出以下结论。 图16 工况7、8、9条件下1~14号岩层的破坏深度Fig.16 Failure depth of rock strata 1~14 under working conditions 7,8 and 9 图17 工况7、8、9条件下1~14号岩层的层间力Fig.17 Interlayer forces of rock strata 1~14 under working conditions 7,8 and 9 图18 工况7、8、9条件下1~14号岩层的破坏模式及相应数量Fig.18 Failure modes and numbers of rock strata 1~14 under working conditions 7,8 and 9 (1) 3种工况条件下,横向节理位置和节理长度变化较大,但是1~14号岩层的层间作用力总是先增大后减小,变化趋势基本保持一致。但是,层间力的曲线形状发生了较大变化。个别岩层(13号岩层)在3种工况条件下发生破坏所需的层间作用力差值较大。 (2) 3种工况条件下,破坏岩层总数一致,且破坏分区特性明显:发生剪切破坏的岩层集中在坡脚区,中上部岩层发生弯曲拉裂破坏。但是,不同破坏区的覆盖范围发生了变化:当坡脚区域的岩层的横向节理位置逐步向边坡表层上移时,发生剪切破坏的岩层数目增加,发生弯曲拉裂破坏的岩层数目减少,即剪切破坏区扩大,弯曲拉裂破坏区缩小。 (3) 3种工况条件下,岩层的破坏位置在坡体中上部比较一致,但是在坡脚区域变化较大。 本文通过计算机随机生成横向节理的位置系数和长度系数来表征横向节理的随机特性,建立随机横向节理反倾向层状边坡模型,探讨反倾向层状节理边坡的破坏启动条件和破坏机理,弥补了现有研究的缺失。以皖南山区的典型反倾向板岩边坡为工程实例,研究了横向节理位置和横向节理长度单独变化,以及两者同时变化对边坡倾倒破坏的影响,得到以下结论。 (1) 不管横向节理位置和横向节理长度如何变化,潜在破坏岩层的层间力总是先增大后减小,且破坏分区特性明显:坡脚区岩层发生剪切破坏,中上部岩层发生弯曲拉裂破坏。 (2) 当横向节理位置或者节理长度发生变化时,层间力的大小也随之发生变化,并且层间力对横向节理长度的变化更为敏感。 (3) 当横向节理位置和节理长度同时改变时,层间力的曲线形状发生了较大变化,个别岩层发生破坏所需的层间作用力差值较大。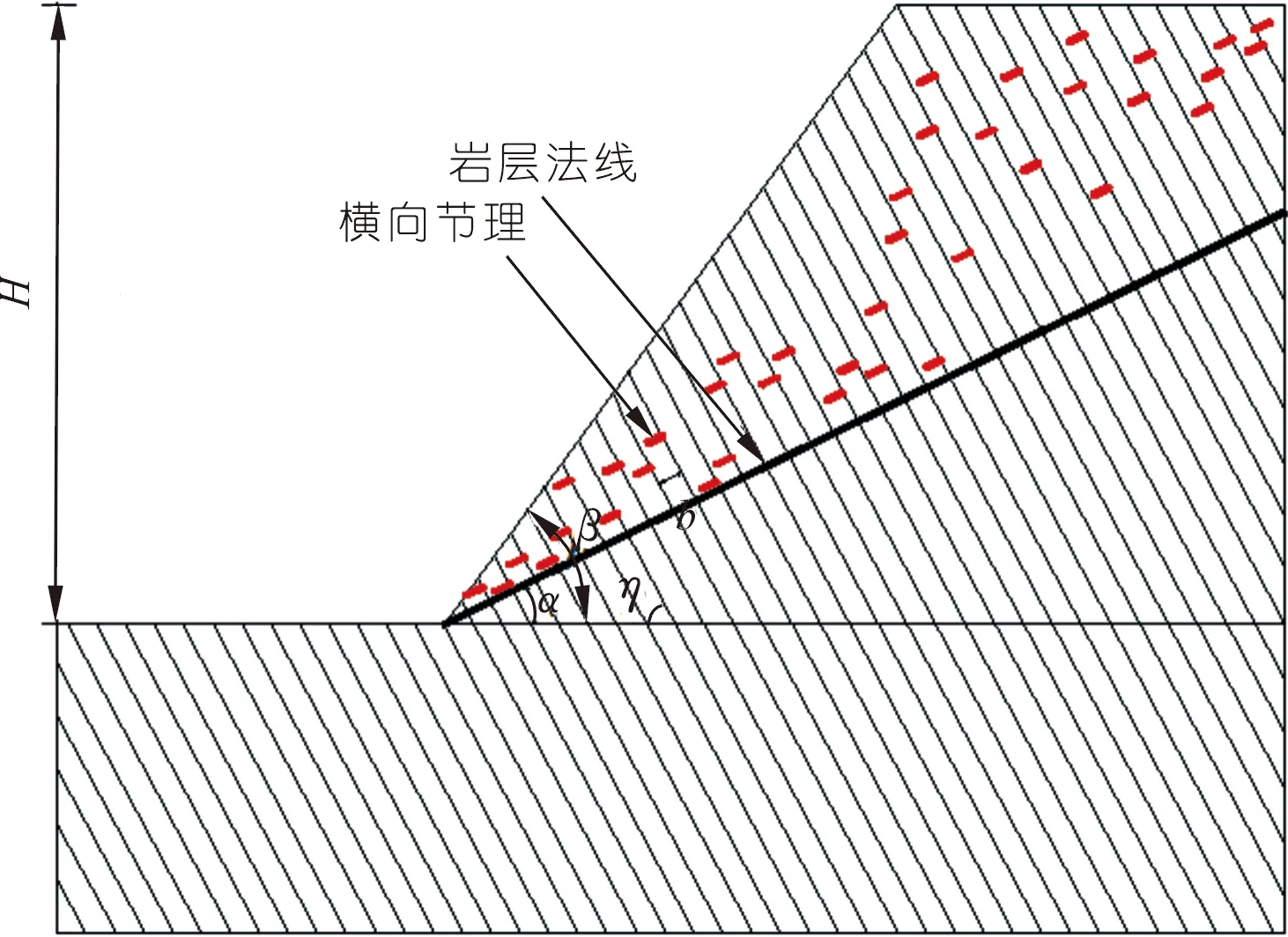
2 反倾向层状节理边坡的破坏机制
2.1 启动条件
2.2 破坏机理
2.3 节理岩体的破坏位置

2.4 岩层破坏所需的层间力

3 算例分析

3.1 横向节理位置对反倾向边坡倾倒破坏的影响

3.2 横向节理长度对反倾向边坡倾倒破坏的影响

3.3 横向节理位置和长度对反倾向边坡倾倒破坏的影响
4 结 论
