四轮驱动拖拉机牵引性能预测模型建立与试验
2023-09-23赵静慧刘孟楠徐立友谢普康
赵静慧 刘孟楠 徐立友 于 硕 谢普康
(1.河南科技大学车辆与交通工程学院,洛阳 471003; 2.洛阳拖拉机研究所有限公司,洛阳 471003;3.智能农业动力装备全国重点实验室,洛阳 471039)
0 引言
牵引性能是拖拉机将使用重力转换为对农机具有效牵引力的能力,决定了耕整和运输作业过程中的整机效率和技术经济性,是拖拉机最重要的使用性能之一[1-2]。拖拉机牵引性能通常由牵引效率、滑转效率、最大牵引力等指标评价[3],其中,驱动轮滑转率同时影响整机牵引效率和最大牵引力,是拖拉机牵引性能的主要影响因素。然而,滑转效率受轮胎、土壤、超前率、载荷波动等复杂因素共同影响,计算分析过程非线性强[4-6]。因此,从轮胎-土壤附着特性入手揭示滑转效率影响机理,提出基于模型的田间牵引性能预测方法是优化拖拉机总体参数与设计方案的重要科学问题,对于改善农业动力装备综合使用性能具有重要意义。
拖拉机田间牵引性能预测方法一直是国外农业动力装备领域研究的热点[7-8],FERVERS[9]提出了采用有限元方法对土壤-轮胎接触面几何形状以及土壤正压力和剪切力分布建模的方法;文献[10-11]提出了基于贯入试验和概率分析的半经验方法,建立了拖拉机行走系在均质土壤中的载荷-沉陷关系和剪切应力-位移关系模型,用于计算整机附着性能;GUY[12]分析了前后轴交互作用对四轮驱动拖拉机牵引效率的影响机理,并开展了田间试验验证;WONG等[13-14]以四轮驱动拖拉机滑转效率最优为目标,分析了前后不协调系数对底盘牵引附着性能的影响机理。国内相关研究较少,张文春等[15-16]基于小功率后轮驱动拖拉机牵引试验数据建立了滑转效率计算经验模型;徐挺[17]建立了四轮驱动拖拉机前后不协调系数优化计算模型。相关研究为四轮驱动拖拉机田间牵引性能预测提供了理论基础,但是均未能充分定量地分析前后轮附着差异、载荷转移和前后运动不协调因素对滑转效率和牵引性能的影响,影响了模型预测的准确性。
本文从拖拉机单个轮胎的驱动特性和载荷特性分析入手,通过引入轮胎指数、机动指数,充分考虑牵引作业过程中的土壤条件、前后桥运动不协调、质心位置转移、前后轮附着特性差异等多变量因素,建立拖拉机牵引驱动模型,提出四轮驱动拖拉机田间牵引性能预测模型与求解算法,开展田间试验,以期为农业动力装备的牵引性能提升提供理论指导。
1 拖拉机牵引性能预测模型
拖拉机牵引驱动模型提出了预测田间性能的理论方法,对前后轮胎、前后轴、轴间、整机分别建模,包含土壤-轮胎模型、轮胎载荷模型、轴的驱动和载荷模型、前后轴间交互模型、整机驱动平衡方程和整机效率模型一系列数学模型。土壤-轮胎模型从单个轮胎的驱动特性入手,分别分析前后轮胎的附着性能。轮胎载荷模型考虑作业过程中的载荷转移导致前后轮垂直载荷的动态变化,从而引起的前后轮胎附着性能的改变。前后轴间交互模型考虑轴间刚性连接的四轮驱动拖拉机前后轴运动不协调因素,得到避免功率循环的最小牵引力。对整机在前进方向、俯仰方向2个自由度建模,不考虑同一轴上左右轮胎的附着和载荷差异,将前后轴的驱动模型合并得到整机驱动平衡方程。通过引入滑转效率、滚动效率及牵引效率模型,对四轮驱动拖拉机整机效率模型进行理论推导。
拖拉机牵引驱动模型包含超越方程组,求解算法是一个迭代过程,系统求解可得到整机牵引性能的重要评价指标为最大牵引力、滑转效率、行走效率等,以及前后轮胎滑转率、前后桥轴荷、前后桥驱动力的动态变化。
1.1 土壤-轮胎驱动模型
采用基于土壤圆锥指数的地面力学方法建立土壤-轮胎驱动模型[18-23]。模型中使用土壤圆锥指数,由圆锥贯入仪的圆锥体探针以稳定的速度插入土壤所需的每单位基底面积的力,用于表征土壤压缩强度和抗剪强度的综合特性[24]。在拖拉机一般耕作深度内,软土或砂土圆锥指数通常为0~700 kPa,中等耕作土壤或壤土圆锥指数通常为850~1 200 kPa,坚实土壤或粘土圆锥指数在1 750 kPa以上[21]。在此基础上引入轮胎指数,表示农用轮胎在兼具粘性与摩擦性质的土壤中的性能[19-20],其计算式为
(1)
式中Cn——轮胎指数
CI——土壤圆锥指数,kPa
b——轮胎断面宽度,mm
d——轮胎直径,mm
Fz——轮胎法向载荷,kN
考虑牵引过程中轮胎与土壤接触时的径向形变比和高宽比因素,引入轮胎机动指数Bn,表征在单个轮胎的牵引性能,随着Bn增加,轮胎的牵引性能得到改善,用于修正轮胎指数,计算式为[21-22]
(2)
式中dΔ——轮胎径向形变量,mm
h——轮胎断面高度,mm
引入轮胎驱动力利用系数,定义为轮胎驱动力与法向载荷之比,是轮胎机动指数与滑转率的函数,用来表征轮胎与土壤接触面受到剪切应力-位移关系。计算式为
(3)
式中GTR——轮胎驱动力利用系数
GT——轮胎驱动力,kN
σ——轮胎滑转率
定义滚动阻力系数为轮胎滚动阻力与法向载荷之比,是轮胎机动指数与滑转率的函数,用来表征轮胎对土壤施加的法向载荷引起下陷而产生的行驶阻力。计算式为
(4)
式中MRR——轮胎滚动阻力系数
MR——轮胎滚动阻力,kN
定义轮胎牵引力利用系数为轮胎能够产生的牵引力与法向载荷之比,由式(3)、(4)可得
NTR=GTR-MRR=
0.88(1-e-0.08Bn)(1-e-7σ)+0.03-
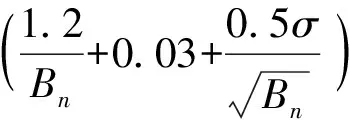
(5)
式中NTR——轮胎牵引力利用系数
由式(5)可知,土壤-轮胎互作过程中的牵引力利用系数可由土壤圆锥指数、轮胎断面宽度与高度、径向形变量、轮胎直径等特征参数组成的函数表达,该模型可以有效表征轮胎载荷、土壤、轮胎等因素对拖拉机牵引性能的影响机理。
1.2 轮胎载荷模型
轮胎载荷模型是描述机组外载的作用下,前后轮胎的垂直载荷动态变化的方程组。图1为拖拉机牵引受力分析情况。由图1可知,在标准牵引试验工况下,拖拉机质心位置与牵引力作用线均在整机纵向对称平面内。
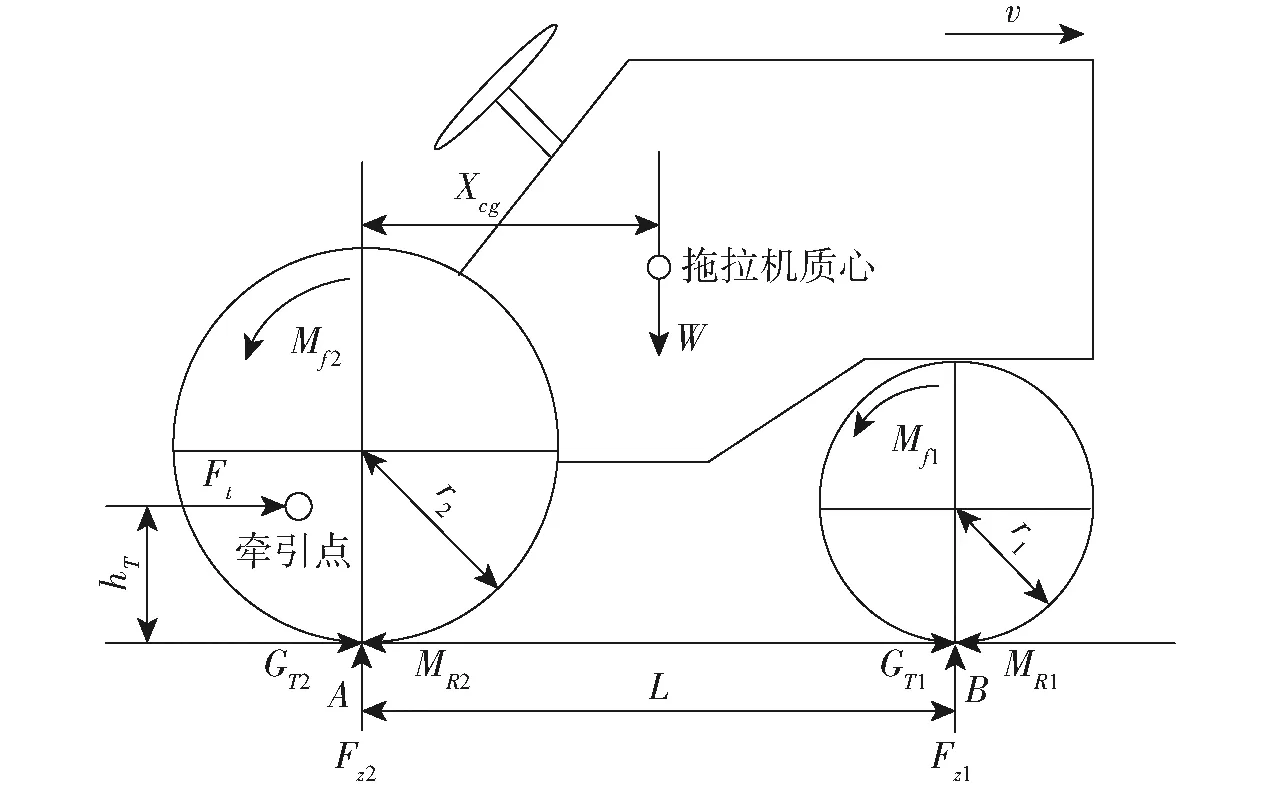
图1 拖拉机牵引受力情况
从受力分析可知,四轮驱动拖拉机前后轮胎的滚动阻力矩为
Mf1=Fz1MRR1r1
(6)
Mf2=Fz2MRR2r2
(7)
式中Mf1——四轮驱动拖拉机前轮滚动阻力矩,N·m
Mf2——四轮驱动拖拉机后轮滚动阻力矩,N·m
Fz1——前轮地面法向反作用力,kN
Fz2——后轮地面法向反作用力,kN
r1——四轮驱动拖拉机前轮半径,mm
r2——四轮驱动拖拉机后轮半径,mm
引入土壤-轮胎驱动模型表征前后轮土壤、轮胎特性,可得包含轮胎机动指数的前、后轮地面法向反力计算式为
(8)
(9)
式中W——拖拉机实际重力,kN
L——拖拉机轴距,mm
Xcg——质心到后轴轴心的纵向距离,mm
hT——牵引点高度,mm
Ft——拖拉机整机牵引力,kN
1.3 拖拉机牵引驱动模型
拖拉机牵引驱动模型是计算滑转效率和预测牵引性能的核心模型,是在轮胎驱动模型和载荷模型的基础上,引入双驱动桥的载荷分配、驱动特性以及整机驱动力平衡、运动不协调等拖拉机整机因素特征建立,具体为:
根据式(3)建立前、后轮胎驱动力利用系数计算式为
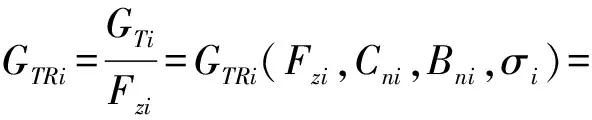
0.88(1-e-0.08Bni)(1-e-7σi)+0.03
(10)
式中i为1代表前轮,为2代表后轮。
根据式(4)建立前、后轮胎滚动阻力利用系数计算式为
(11)
根据式(10)、(11)建立前、后轮胎牵引力利用系数计算式为
NTRi=GTRi-MRRi=NTRi(Fzi,Cni,Bni,σi)=
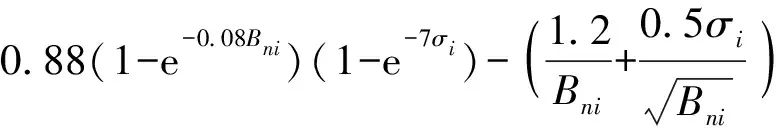
(12)
设定拖拉机质心位置坐标与牵引力延伸线处于垂直于地面的同一平面内,则同驱动桥两侧的驱动轮载荷相等,由式(8)、(9)可得到前后桥轴荷计算式为
(13)
式中W1——拖拉机前驱动桥轴荷,kN
W2——拖拉机后驱动桥轴荷,kN
导出前后桥驱动力计算式为
(14)
式中Fq1——拖拉机前驱动桥驱动力,kN
Fq2——拖拉机后驱动桥驱动力,kN
拖拉机驱动力平衡方程为
Fq=Ft+FRR
(15)
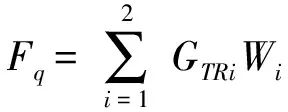
(16)
(17)
(18)
式中Fq——四轮驱动拖拉机总驱动力,kN
FRR——拖拉机整机滚动阻力,kN
四轮驱动拖拉机牵引作业时,前后桥间的传动系为刚性闭锁式联接,实际速度相等;由于前后驱动轮对土壤的压实作用存在时序,且轴荷、轮胎规格不同,前后桥作业时的地面附着系数存在差异,因此需要针对四轮驱动拖拉机的前后桥分别设计不同的理论速度避免驱动轮出现严重滑转现象,采用前后桥运动不协调系数表示前后驱动轮理论速度差异,计算式为
(19)
式中ε——前后桥运动不协调系数
VL1——前桥理论速度,km/h
VL2——后桥理论速度,km/h
拖拉机实际作业车速为
V=V1=V2
(20)
式中V——拖拉机实际作业速度,km/h
V1——前桥实际作业速度,km/h
V2——后桥实际作业速度,km/h
拖拉机理论作业车速为
(21)
式中VL——拖拉机理论作业速度,km/h
将式(21)代入式(20)可得
V=VL1(1-σ1)=VL2(1-σ2)
(22)
式中σ1——前轮滑转率
σ2——后轮滑转率
将式(19)代入式(22)推导出前后轮滑转率与前后桥运动不协调系数的关系式为
σ1=σ2+ε(1-σ2)
(23)
四轮驱动拖拉机滑转效率是整机驱动实际输出功率与理论驱动功率之比,考虑前后桥运动不协调性后,整机理论驱动功率为前后桥总驱动功率,导出滑转效率计算式为
(24)
式中ησ——四轮驱动拖拉机滑转效率
将式(21)代入式(24)可得
(25)
由式(25)可知,滑转效率可由前后桥驱动力分配及前后轮滑转率的函数表征。结合式(3)、(5),可揭示四轮驱动拖拉机滑转率同时受轮胎、土壤、拖拉机前后桥运动不协调的影响机理。
由式(15)、(18)可导出四轮驱动拖拉机滚动效率模型为
(26)
式中ηf——四轮驱动拖拉机滚动效率
由式(25)、(26)可导出四轮驱动拖拉机牵引效率预测模型为
ηT=ηDηc=ησηfηc=
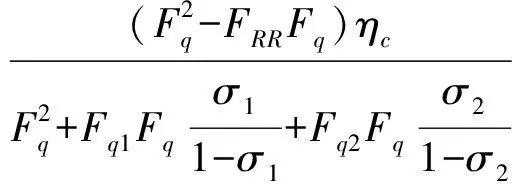
(27)
式中ηT——四轮驱动拖拉机牵引效率
ηD——四轮驱动拖拉机行走效率
ηc——拖拉机传动效率
将单个轮胎模型、驱动轴及轴间运动模型及整机模型组成四轮驱动拖拉机牵引驱动模型路线图如图2所示,该模型可有效表征四轮驱动拖拉机牵引效率受轮胎规格、土壤特性、整机前后桥运动不协调特性、传动系统综合影响的机理。
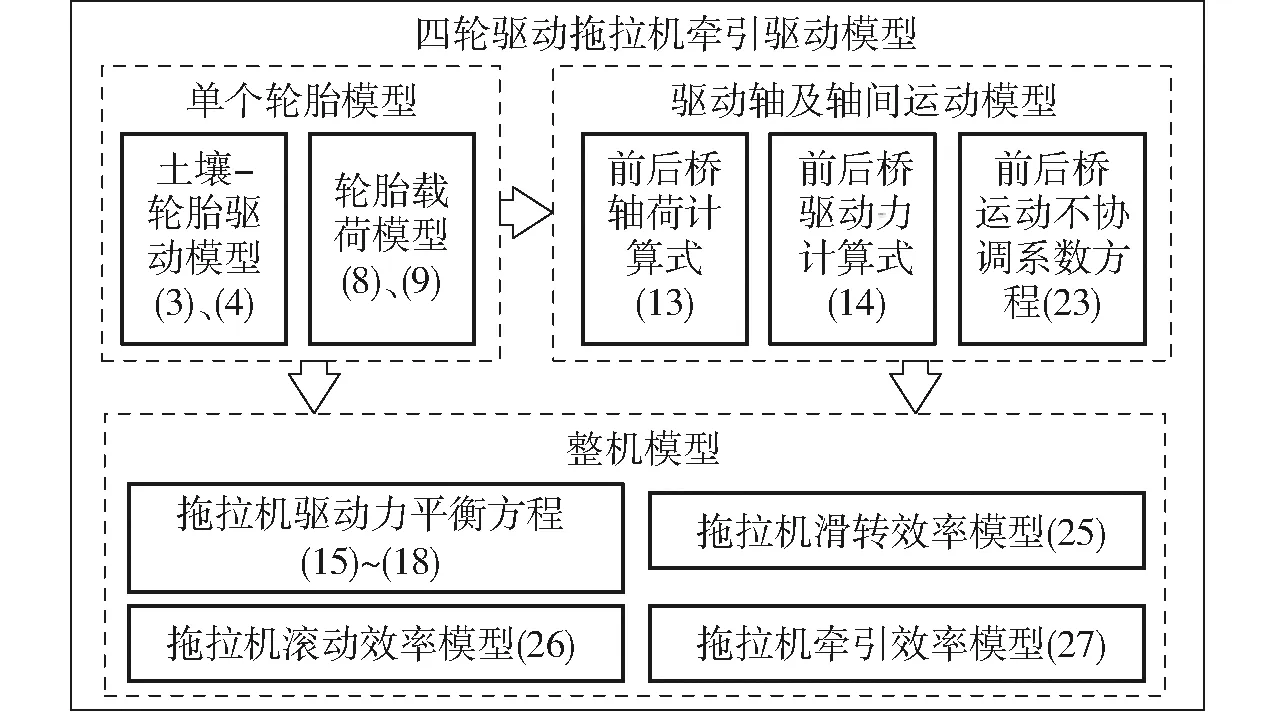
图2 四轮驱动拖拉机牵引驱动模型建立技术路线图
2 求解算法
由于模型内部和各模型间存在迭代的特性:整机牵引力的发挥是所有单个驱动轮能够发挥的牵引力之和,单个轮胎的牵引特性是其法向载荷的函数,而单个轮胎上的法向反作用力取决于整机牵引力和前后驱动轮滚动阻力系数。模型无法自上而下或一次性计算求解,求解过程需要建立双维度迭代算法。
求解算法及流程见图3。内层将后轮滑转率进行迭代,由前后桥运动不协调系数方程式(23)解出前轮滑转率,由土壤-轮胎驱动特性式(10)~(12)分别解出前后轮胎的驱动力系数GTR、滚动阻力系数MRR及牵引利用系数NTR。由前后桥驱动力计算式(14)得到前后驱动桥驱动力。由拖拉机驱动力平衡方程(16)~(18)得到整机滚动阻力、牵引力、驱动力。外层将后轮法向载荷Fz2进行迭代,初始条件等于静态载荷,按照5 N的步长更新,终止条件为后驱动桥轴荷W2达到为80%的整机重量。模型最终可求解出所有挂钩牵引力范围内的前后滑转率、前后驱动力和滚动阻力,即可根据式(25)~(27)计算整机行走效率。
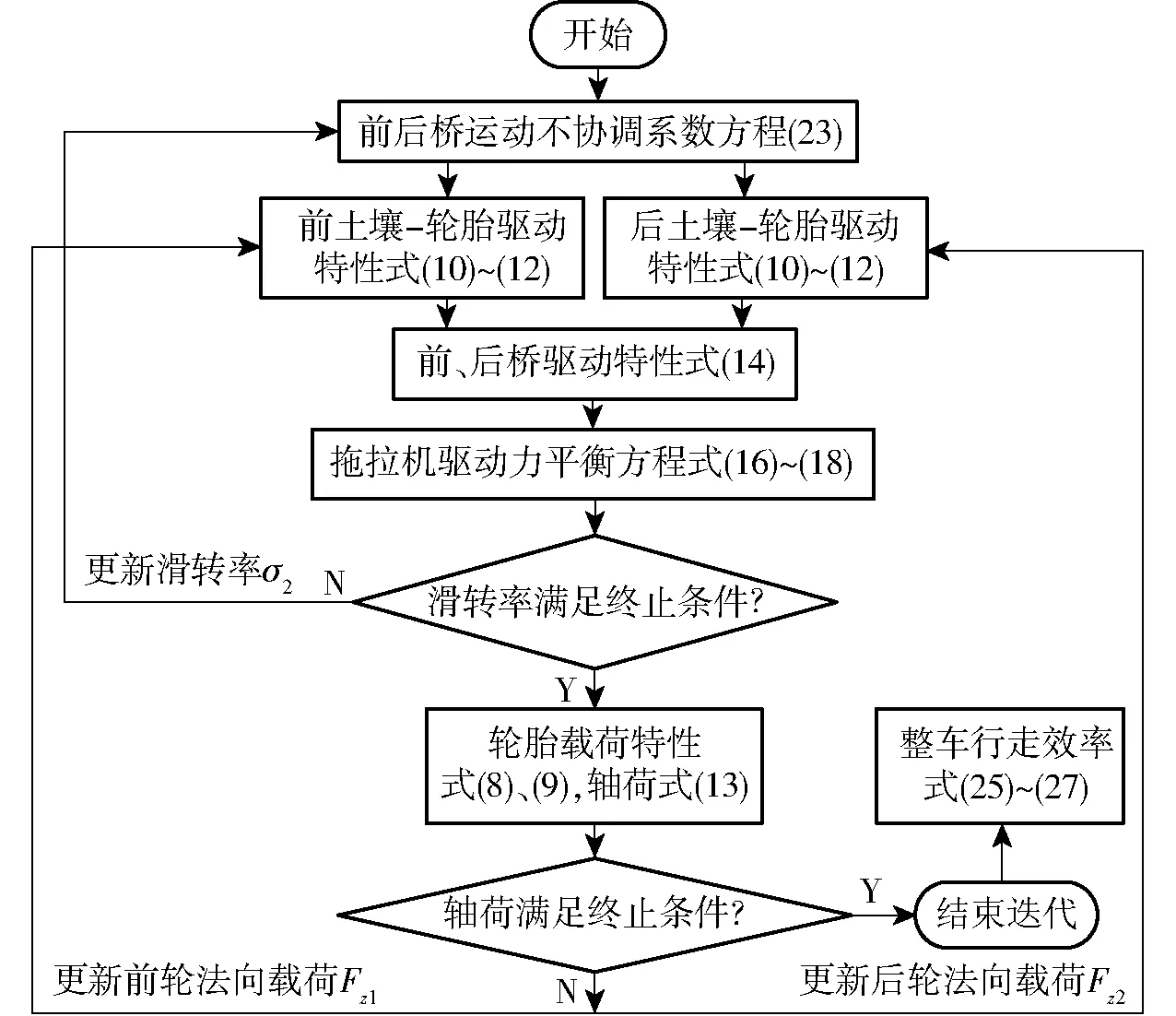
图3 拖拉机牵引性能仿真流程图
3 实例分析
以东方红某165 kW拖拉机为实例,整机参数如表1所示,在土壤圆锥指数为1 725 kPa的农用土壤环境下,通过在Matlab环境中按照图2中的模型建立路线图分别建立土壤-轮胎模型、驱动轴及轴间运动模型、整机模型并按照图3中的流程建立求解算法,建立数学模型开展仿真分析。
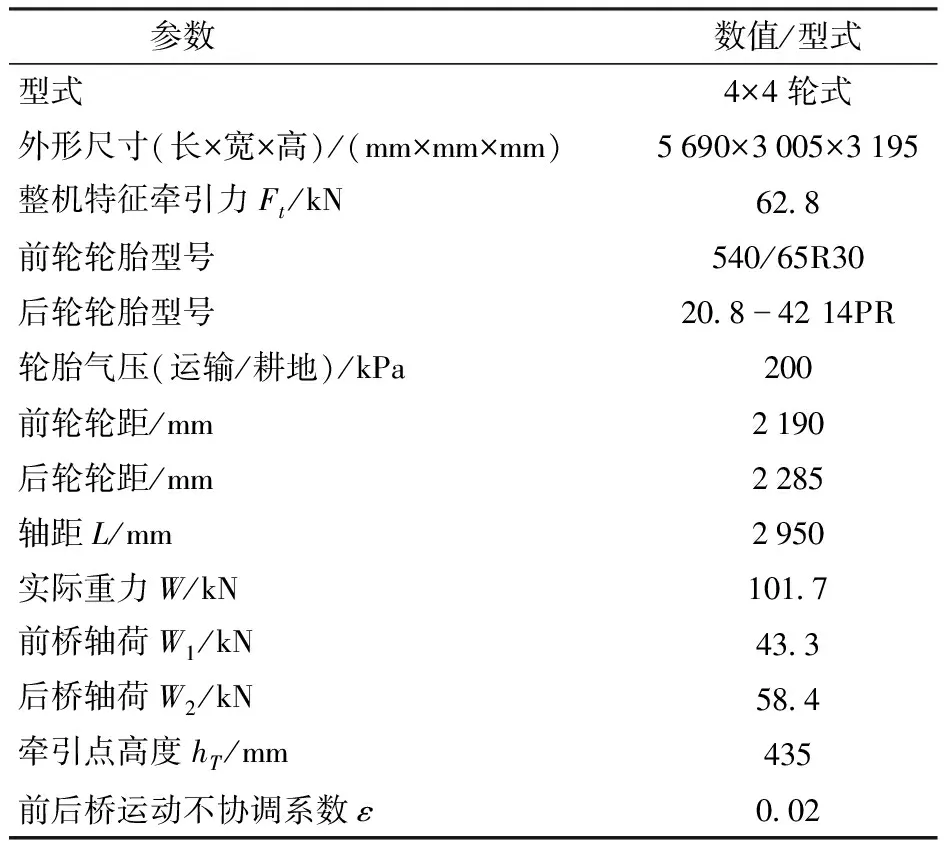
表1 实例分析整机参数
图4为土壤-轮胎驱动特性情况。其中图4a为前后轮驱动利用系数与牵引力的关系,由图4a可知,牵引力范围内,前轮的驱动利用系数始终高于后轮;当牵引力达到特征值时,GTR1=0.71,GTR2=0.68;主要原因是前桥的静态轴荷小于后桥,前驱动轮的法向载荷较小,随着牵引力逐渐增大,质心位置后移,前桥减重,后桥增重,前轮驱动力利用系数的变化率小于后轮。
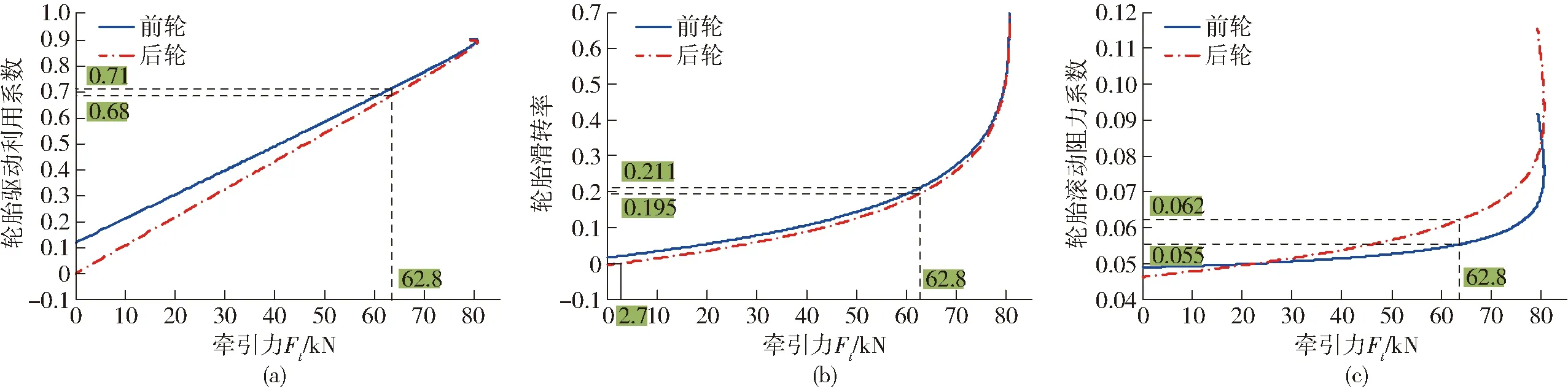
图4 土壤-轮胎驱动特性
图4b为前后轮胎滑转率情况。由图可知,当Ft<2.7 kN时,σ1>0,σ2<0,VL1>V>VL2;由于前后桥运动不协调,整机前驱动轮理论速度较高,驱动力较大,滑转较高;在整机的推进作用下,后驱动轮理论速度小于整机推进速度,同时出现滚动与滑移,对整机起到了制动作用。产生这种情况的原因是当牵引载荷较低时,由于前后桥运动不协调性导致前、后理论速差较大,四轮驱动拖拉机出现了明显的功率循环。当Ft=2.7 kN时,σ1>0,σ2=0,VL1>V=VL2,此时后驱动轮呈纯滚动状态。当Ft>2.7 kN时,σ1>σ2>0,VL1>VL2>V,前后驱动轮都出现了滑转的情况,功率循环消除,前后轮胎均发挥驱动作用;此时由于运动不协调系数导致前驱动轮理论速度较高,滑转率较大。
图4c为前后轮滚动阻力系数与牵引力的关系。由图4c可知,滚动阻力系数随挂钩牵引力而增大。当牵引力达到容许特征值之前,轮胎的滚阻系数的增加较小,MRR1=0.049~0.055,后轮滚阻系数MRR2=0.045~0.062。当牵引力超过容许特征值后,由式(4)可知,前后轮滑转率快速增大,引起了滚动阻力系数的快速增加。当牵引力增大到80 kN左右,轮胎滚动阻力系数快速增大,导致整机滚动阻力的快速增大,引起牵引力下降,得出该型号四轮驱动拖拉机在土壤圆锥指数为1 725 kPa的农用土壤环境下的最大牵引力为80 kN。
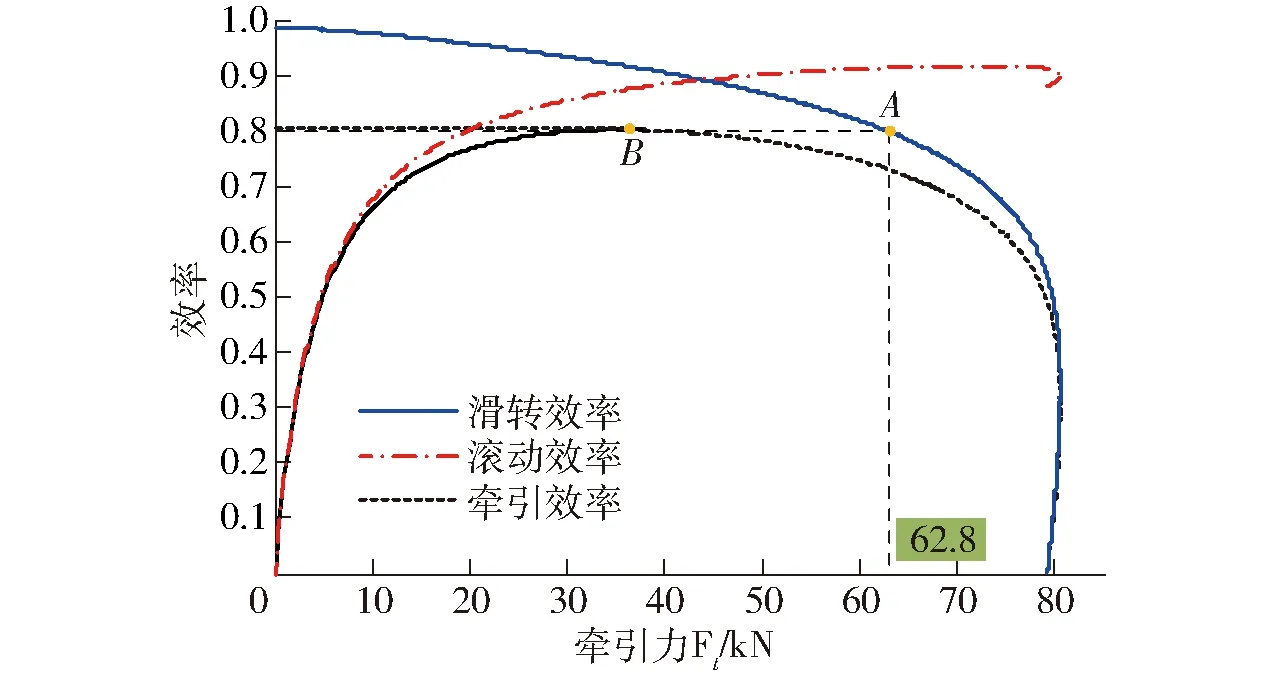
图5为前后桥载荷与驱动特性。图5a为前后桥轴荷与牵引力的关系,由图5a可知,由于轴荷转移情况与牵引力大小呈线性关系,W1随Ft的增大而减小,W2随Ft的增大而增大。当Ft达到容许特征值时,W1=31.4 kN,占整机重力的32%,前桥轴荷减重达到24.4%。图5b为前后桥驱动力与牵引力的关系,由图5b可知,当Ft≤16.4 kN时,Fq1≥Fq2,前桥分配的驱动力较大;当Ft>16.4 kN时,Fq1 图5 前后桥载荷和驱动特性 图6为四轮驱动拖拉机牵引性能计算结果。由图6可知,整机在容许滑转率点A时的牵引力为62.8 kN,行走效率为0.731,滚动阻力系数达到0.06;在行走效率最高点B处牵引力为36 kN,行走效率为0.802,滑转率为0.081,滚动阻力系数为0.052。根据国家拖拉机质量检验检测中心出具的该型号拖拉机标准跑道环境的牵引性能试验报告,整机达到容许滑转率时的行走效率为0.86,最高行走效率可达0.93,对照分析结果可知,实际农用土壤条件对四轮驱动拖拉机牵引性能的影响较大,降幅为10%~15%。此外图中,当ησ=0.8时,即滑转率达到特征滑转率0.2时,四轮驱动拖拉机Ft达到容许特征值62.8 kN。对照图4b可以看出,此时,σ1=0.211,超过容许滑转率;σ2=0.195,低于容许滑转率,说明建立的滑转效率模型体现出了四轮驱动拖拉机前后桥运动不协调性与前后轮胎-土壤附着性能差异,有效性较好。 图6 牵引性能计算结果 开展实机田间牵引负荷测试,验证提出的牵引性能预测方法的有效性。试验总体参照GB/T 3871.9—2006《农业拖拉机试验规程 第9部分 牵引功率试验》开展,被试对象为实例分析对象拖拉机,轮胎胎压、整机参数如表1所示。试验地点为洛阳拖拉机研究所有限公司孟津崔沟田间全地型试验场,测试环境为玉米茬地,测试土壤圆锥指数为650 kPa左右。被测变量为牵引力、不同牵引力下的前后轮胎滑转率、轮胎滚动阻力。试验采用TY160型负荷车、PCM-6851型车辆综合性能测试仪、OMRON E6B2-CWZ3E型转数传感器和BLR-1M10T型拉压力传感器。 图7为田间试验原理及主要试验设备情况。试验过程中,负荷车加载最大功率为175 kW,最大加载力为120 kN,负载牵引力从0 kN开始,以1 kN为步长线性增加,至驱动轮全滑转后终止增大;测试作业距离取40 m;测试速度为3.5 km/h。被测变量的测试方法为: 图7 试验原理及主要试验设备 牵引力:被试拖拉机与负荷车之间通过拉压力传感器和钢索连接,由安装在拖拉机牵引挂钩处的拉压力传感器测量负荷车施加的牵引力。 轮胎滑转率:滑转率无法直接测量,采用同一距离法测量拖拉机在负荷车施加的不同牵引负载下作业相同距离驱动轮转过的圈数,前后驱动轮转动的圈数由安装在拖拉机驱动轮上的霍尔传感器测量,根据驱动轮圈数计算轮胎滑转率为 (28) 式中σ′i——轮胎滑转率测量值 NAi——无牵引负载状态下轮胎转过的圈数 NBi——逐渐增加牵引负载后轮胎转过的圈数 轮胎滚动阻力:测试滚动阻力时,被试拖拉机发动机熄火、挂空挡,使传动系主离合器完全分离后,由负荷车反向拖动被试拖拉机,由拉压力传感器测量得出滚动阻力。 通过河南科技大学设计的车辆综合性能测试仪对单一采样步长内的拉力、轮胎转动圈数等信号进行整合处理,得出测试过程中的牵引力、轮胎滑转率、轮胎滚动阻力;上传至上位机端。 依照与试验相同的拖拉机整机参数及土壤环境,在Matlab环境中建立该实例拖拉机的田间牵引性能预测模型,得到仿真结果。选择相关研究[15]中使用的拖拉机牵引性能模型作为对照组,并建立对照组模型,开展对比分析。将仿真、试验数据与相关研究中的对照组结果进行对照,结果如图8所示。 图8 滑转率、滚动阻力试验值和仿真值对比 图8a为滑转率对照结果,对比在该点处的仿真值、试验值及对照组的值,如表2所示。采用提出的四轮驱动拖拉机田间牵引性能预测分析结果中,整机全滑转时的最大牵引力仿真值为64.8 kN,特征滑转率对应的牵引力仿真值为51.2 kN;最大牵引力试验值为63.9 kN,特征滑转率对应的牵引力试验值为49.9 kN;仿真值在最大牵引力与特征滑转率对应的牵引力上的误差分别为1.41%与1.74%。对照组中,最大牵引力仿真值为38.1 kN,特征滑转率对应的牵引力为26.5 kN,在最大牵引力与特征滑转率对应牵引力上的误差分别为40.37%与46.89%。提出的四轮驱动拖拉机田间牵引性能预测模型对滑转率、滑转效率等指标的仿真精度较好。 表2 仿真值、对照组与试验值特征指标对比 图8b为滚动阻力指标对照结果。由图8b及表2 可知,提出的四轮驱动拖拉机田间牵引性能预测分析结果中,未施加负载牵引力时的滚动阻力仿真值为7.78 kN,最大牵引力仿真值为64.8 kN,当牵引力超过64.8 kN后,滚动阻力持续增大,降低牵引力输出能力;未施加负载牵引力时的滚动阻力试验值为7.83 kN,误差为0.64%;对照组中,滚动阻力仿真值始终保持为6.97 kN,未施加牵引力处的误差为10.9%,误差较大。此外,由滚动阻力测试方法可知,试验过程中仅能通过负荷车反向拖动的情况测试出未施加牵引力状态下整机的滚动阻力,当施加牵引力后,拉压力传感器仅能测出施加在拖拉机牵引挂钩上的牵引力,因此难以有效测出加载状态下拖拉机滚动阻力的具体变化情况;但是,从滑转率测试结果中对照仿真值与试验值的最大牵引力指标对比情况可以看出误差较小,可以证明滚动阻力仿真的效果较好。 由图8可知,仿真值总体上可以较为准确地体现出牵引性能核心指标牵引力、滑转率、滚动阻力的变化趋势,采用均方根误差(Root-mean-square error,RMSE)评价模型的有效精度。计算可得,提出的四轮驱动拖拉机田间牵引性能预测分析仿真值滑转率均方根误差为0.023 7,滚动阻力均方根误差为0.23 kN; 对照组滑转率均方根误差为0.219,滚动阻力均方根误差为1.66 kN。因此,提出的四轮驱动拖拉机田间牵引性能预测分析方法总体与实测值的偏差较小,模型的准确度较高。 (1)通过建立土壤-轮胎驱动模型、轮胎载荷模型与拖拉机牵引驱动模型,导出了包含轮胎规格、土壤特性、整机前后桥运动不协调特性、传动效率的四轮驱动拖拉机牵引效率预测模型,揭示了影响机理。 (2)提出了基于双维度迭代的牵引性能预测算法,制定了求解流程,有效解决了模型多变量、非线性导致的求解难题;开展了实例分析,预测了四轮驱动拖拉机在农用土壤条件下的牵引力、滑转率、滚动阻力、牵引效率等牵引性能指标。 (3)设计了田间牵引试验方案,选择现有预测模型作为对照组,开展了试验,结果表明:农用土壤条件下,对照实测值,提出的牵引性能预测方法中滑转率均方根误差为0.023 7,滚动阻力均方根误差为0.23 kN,总体偏差较小,较对照组精度提升较大,验证了提出的四轮驱动拖拉机田间牵引性能模型及预测方法的有效性。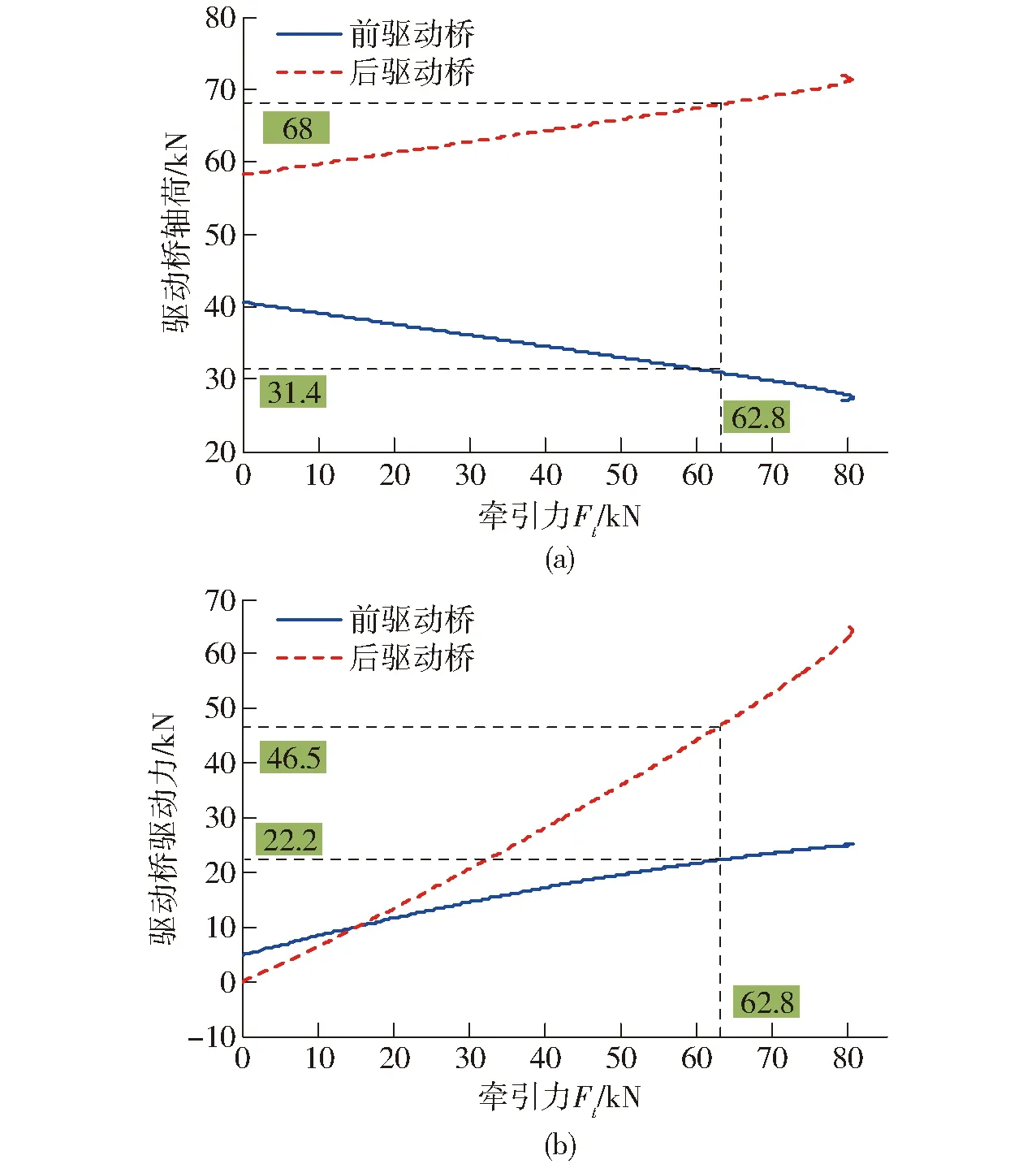
4 试验验证

5 结论
