基于最大熵原理的喷雾液滴粒径分布预测研究

彭燕祥 张 华 何贵成

(华北电力大学水利与水电工程学院,北京 102206)

0 引言

喷雾是一种复杂的水气两相流运动,在许多工程应用中起着重要的作用,如发动机燃料的燃烧[1]、农业喷灌技术[2-3]、喷雾降温[4-5]等。液滴粒径分布是喷雾过程的质量、动量和能量输运的关键参数,特别是在农业灌溉以及农药喷撒方面,雾滴粒径是影响灌溉液滴以及农药的飘移、沉降的关键因素之一,如何确定喷雾中液滴的粒径分布已成为一个重要的科学问题。

近年来,国内对农业灌溉以及农药喷撒过程中雾滴谱的研究逐渐趋热。喷雾液滴粒径分布是喷头设计以及评价雾化效果的重要指标[6],因此,许多学者针对不同的应用场景,对喷嘴雾化的粒径分布进行了大量的实验研究。如韩文霆等[6]利用2D视频雨滴谱仪,对喷头喷洒液滴的粒径分布进行了测量。李红等[7]采用改进的色斑法,对喷头喷洒雨滴的粒径分布进行测量。雾滴的分布特性通常用雾滴谱表示,雾滴的粒径分布与雾化器的设计及雾化效果有着直接的关系[8]。

目前的喷雾液滴粒径分布函数主要分为经验分布和理论分布两类。经验分布是通过大量的实验研究,得到液滴粒径分布的经验公式,如Nukiyama-Tanasawa分布[9]以及Rosin-Rammler分布[10]和上限函数分布等[11-12]。理论分布包括正态分布、对数正态分布(Logarithmic normal distribution,LN)[13-14]以及最大熵分布[8],其中最大熵分布应用最为普遍。

SELLENS等[15]首先提出运用最大熵模型预测液滴粒径分布的思路。随后SELLENS运用物理守恒约束的最大熵(Maximum entropy method,MEM)模型,对雾化液滴粒径分布进行预测研究[16]。研究表明,通过质量守恒推导的最大熵模型在液滴粒径分布的预测中,预测峰值较实验值,会向较大液滴直径方向偏移。CAO等[17]给出的解决办法是对分布模型参数进行修正。随后王婕等[18]基于最大熵原理,通过最小二乘法对参数的修正提出了优化。

可见,基于物理守恒为约束机制的最大熵分布预测模型,在目前的研究中对液滴粒径分布的预测并不理想。目前常用的解决办法是引入参数,或对参数进行修正,但是主观引入参数会造成一定的误差,影响预测精度,且在复杂的喷雾环境下,物理守恒约束条件的源项求解相对比较困难。因此,本文基于最大熵原理,通过平均直径约束条件,构建雾滴粒径数量概率密度分布模型(Maximum entropy principle,MEP),应用于喷雾液滴粒径数量概率密度分布的研究中。

1 研究方法

1.1 对数正态分布

对数正态分布函数的数学表达式为

(1)

式中μ——尺寸参数

σ——形状参数

x——随机变量

1.2 液滴粒径分布函数

信息熵由SHANNON[19]首次提出,能够反映一个宏观系统的微观状态的不确定性,其数值是该状态下包含信息量的数学度量。

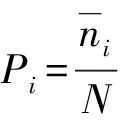
(2)

式中S——信息熵k——常数

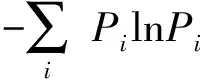
推断液滴粒径分布的可用信息约束数学表达式为

(3)

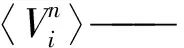
当n=1时,式(3)为数学期望的表达式。

假设液滴在表面张力的作用下,呈球形分布,则

(4)

式中Di——将液滴直径按从小到大进行排序分组,第i组液滴的代表直径,μm

则式(3)可以写成

(5)

令3n=r,则约束条件为

(6)

将Di无量纲处理得

(7)

其中

式中D30——质量平均直径,μm

Di无量纲处理后式(6)可表示为

(8)

其中

Pi满足归一化条件约束

(9)

将式(8)、(9)作为约束条件,利用拉格朗日乘数法构造函数L(Pi),即

(10)

式中λ0、λr——拉格朗日乘子

令L(Pi)对Pi的偏导数等于0,得到Pi的表达式为

(11)

式中a——最大熵分布系数

(12)

假设液滴粒径的变化是连续的,式(12)可以写为

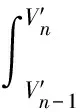
(13)

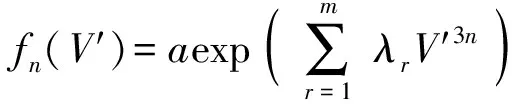
(14)

则

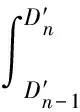
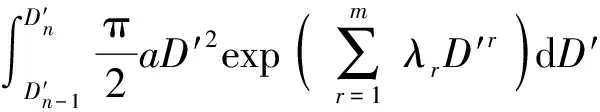
(15)

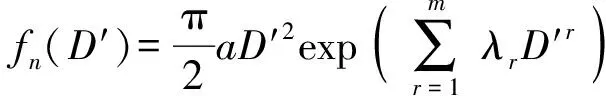
(16)

式中fn(D′)——雾滴粒径连续分布的概率密度分布函数

定义MEPZ为最大熵分布函数fn(D′)的最高阶次Z(Z=1,2,…),即式(16)中m=Z。

则可构建方程组为

(17)

其中

式中Dmin——液滴最小直径,μm

Dmax——液滴最大直径,μm

式(17)中一般将喷雾液滴的最小无量纲直径D′min取零,D′max的取值对液滴粒径分布规律没有实质的影响[14],只需要取值足够大即可,本文计算时取D′max=3.5。

又因为平均直径定义为

(18)

则式(17)可以写成

(19)

式(19)表示方程数为Z+1的方程组,a及λ1、λ2、…、λZ为方程的Z+1个未知数,方程组是封闭的。由于方程组是一个带定积分的非线性方程组,所以方程的求解只能通过数值求解方法。

1.3 液滴的粒径分布与Dv0.1、Dv0.5、Dv0.9 的关系

农业航空中常用平均直径Dv0.1、Dv0.5、Dv0.9来评价喷嘴雾化效果,其中Dv0.1表示雾滴累计分布为10%的雾滴直径,即小于此雾滴直径的雾粒体积占全部雾粒体积的10%;Dv0.5表示雾滴累计分布为50%的雾滴直径;Dv0.9表示雾滴累计分布为90%的雾滴直径。通过求解式(19)可以得到液滴的粒径分布函数fn(D′)的表达式,即能求出各种液滴粒径范围所占百分比。

分布函数fn(D′)确定,则直径为D′i的概率密度可以表示为fn(D′i),则粒径为D′i的液滴数n(D′i)可以表示为

n(D′i)=Nfn(D′i)

(20)

则粒径为D′i液滴的体积Vol(D′i)可以表示为

(21)

将Dv0.1、Dv0.5、Dv0.9用D30无量纲化为D′v0.1、D′v0.5、D′v0.9。

根据Dv0.1的定义可得,液滴粒径在[0,D′v0.1]的液滴体积占总体积的10%,数学表达式为

(22)

方程中只有D′v0.1为未知数,所以在分布函数fn(D′)确定时,可以通过式(22)对D′v0.1进行求解。

同理可得D′v0.5、D′v0.9与粒径分布函数的关系为

(23)

(24)

1.4 平均直径计算

求解式(19),需对无量纲平均直径D′r0进行计算。D′r0可以通过两种方法进行计算:①通过实验数据计算。通过实际的实验测量数据,根据式(7)、(18)直接确定无量纲平均直径D′r0。②通过经验公式进行计算。通过实际的工况条件:喷嘴类型、喷嘴直径等,来求解平均直径。例如RIZK等[20]、ELKOTB[21]提出了索特尔直径(SMD)D32的经验公式,WOOTAE等[22]提出了质量平均直径D30的经验公式。DUMOUCHEL等[23]给出了平均直径系列的关系表达式

(25)

式中c、u——常数

Dcu、Dr0——一系列平均直径,μm

Γ——伽马函数

可以推导出平均直径与D32的关系为

(26)

在已知质量平均直径D30或D32的情况下,通过式(25)能求解任意一个平均直径。

根据式(26),D30可以表示为

(27)

无量纲平均直径D′r0r可以表示为

(28)

2 预测模型优选

2.1 液滴粒径分布数值计算

预测模型优选的求解过程采用有实验数据的求解方法。采用FU[24]的环形鼓风喷嘴雾化实验数据进行研究,喷嘴示意图如图1所示,其中填充部分为喷嘴结构,未填充部分为流体通道。具体工况如表1所示。

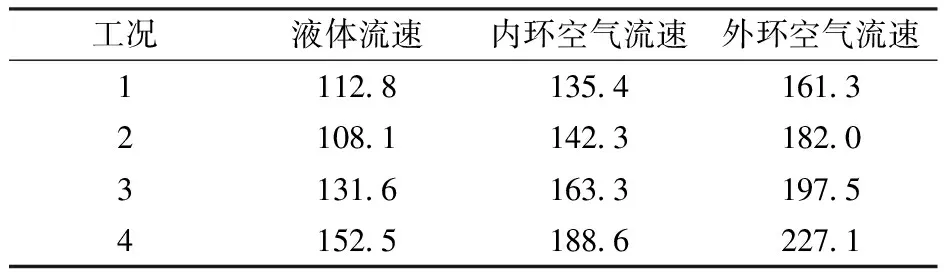
表1 环形鼓风喷嘴雾化实验工况

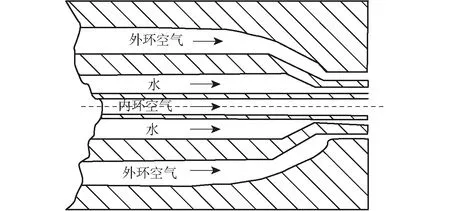
图1 环形鼓风喷嘴示意图

根据各工况下的实验数据,计算得到雾化液滴的算术平均直径D10、表面积平均直径D20以及质量平均直径D30,具体见表2。

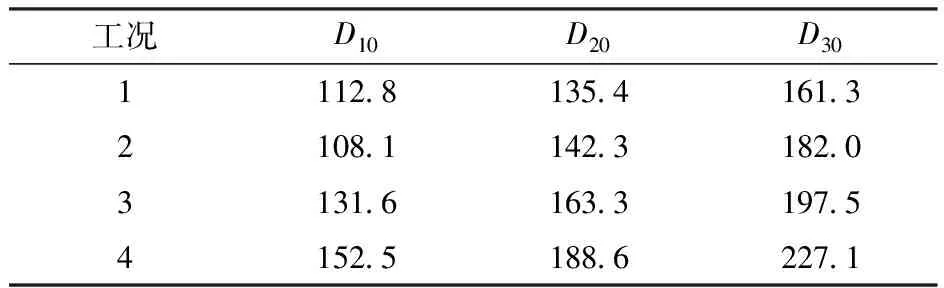
表2 环形鼓风喷嘴雾化实验的液滴平均直径

图2为工况1条件下液滴粒径数量概率分布的预测数据与实测数据对比,图2中的MEP1～MEP3分别表示式(16)最高次阶为1～3的最大熵分布函数,从图2和表3可知,各分布函数都能对液滴分布的趋势进行预测,相关系数R均在0.85以上。LN分布函数与MEM分布预测的峰值偏大。液滴分布的峰值在D′i=0.5附近。MEM分布的预测结果峰值偏向于液滴直径较大一侧,预测峰值在D′i=0.7附近,其他分布函数对于液滴分布的峰值预测比较理想,分布峰值都在D′i=0.5附近。本文构建的预测模型MEP1、MEP2、MEP3的预测结果较为理想,均方根误差(RMSE)均低于0.1,相关系数均高于0.95。

图3为工况2条件下液滴粒径数量概率分布的预测数据与实测数据对比,从图3和表3可知,LN和MEM分布函数预测的效果较差。液滴分布峰值直径在D′i=0.3附近,MEM和MEP1以及LN分布的预测结果峰值偏向于液滴直径较大一侧,MEM预测分布峰值直径在D′i=0.6左右,MEP1和LN预测分布的峰值直径在D′i=0.4附近。MEP2、MEP3分布模型的预测结果较为理想,预测分布峰值均在D′i=0.3附近,与实验值较为吻合,预测值与实验值的相关系数均为0.965,均方根误差为0.135、0.134。

图4为工况3条件下液滴粒径数量概率分布的预测数据与实测数据对比,从图4和表3可知,各分布函数预测的液滴分布结果和实验值的相关系数均在0.8以上。LN分布函数和MEM分布预测的峰值相当,峰值相对于实验值略微偏大。MEM和MEP1以及LN分布的预测结果峰值偏向直径较大一侧,MEM预测的分布峰值直径在D′i=0.7附近,MEP1以及LN分布预测的分布峰值直径在D′i=0.46附近,实验液滴分布峰值在D′i=0.37附近。MEP2、MEP3分布模型的预测结果较为理想,预测的分布峰值均在D′i=0.37附近,与实验数据吻合。MEP2和MEP3模型的预测值几乎重合,预测值与实验值的相关系数为0.989、0.988,均方根误差为0.060、0.062。

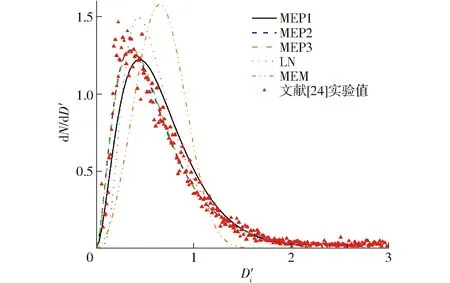
图4 工况3液滴粒径数量概率密度分布预测与实测数据对比

图5为工况4液滴粒径数量概率分布的预测数据与实测数据对比,从图5和表3可知,LN、MEM和MEP1分布的预测结果峰值偏向于直径较大一侧,MEM预测峰值分别在D′i=0.69附近,实验液滴分布峰值在D′i=0.38附近,MEP2、MEP3分布模型的预测结果的峰值均在D′i=0.38附近,与实验数据吻合。MEP2和MEP3模型的预测值几乎重合,预测值与实验值的相关系数均为0.99,均方根误差为0.070、0.068。

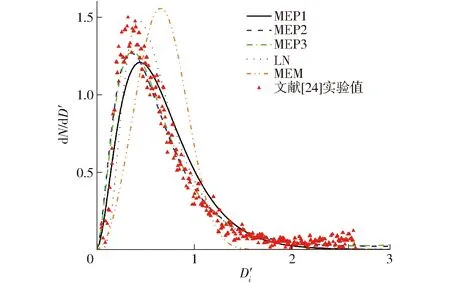
图5 工况4液滴粒径数量概率密度分布预测与实测数据对比

2.2 结果分析

4种工况条件下各分布模型预测数据与实测数据的相关系数与均方根误差统计,如表3所示。

通过2.1节的分析,可以看出MEP2和MEP3的预测效果最好。MEP3的预测曲线与MEP2的预测曲线在4种工况条件下都比较接近,几乎重合。MEP2模型含有3个参数,而MEP3含有4个参数。因此采用赤池信息准则(Akaike information criterion,AIC)对两个模型展开进一步比选研究,AIC最小的模型为最优模型。

AIC准则函数定义为

(29)

式中kn——模型中参数个数

Ne——实测样本数目

MEP2和MEP3模型对应的AIC结果如表4所示。从表4可以看出,工况1、2、3情况下MEP2的AIC均比MEP3的低,在工况4条件下,由于液体和内外环空气的流速都较大,使得液体雾化的环境更加复杂,采用3个约束条件的MEP3预测模型的预测效果相对MEP2模型偏好,MEP3比MEP2的AIC低,但从相关系数和均方根误差来看,MEP3与MEP2结果相差并不大。综合考虑,一般情况下MEP2模型对喷嘴雾化液滴粒径分布的预测效果更好。最优的MEP2分布预测模型为

(30)

对比MEP1、MEP2和MEP3可以发现,MEP1采用了平均直径D10的约束,MEP2采用了平均直径D10、D20的约束,MEP3采用了平均直径D10、D20和D30的约束。通过增加平均直径约束条件有助于提高分布模型的预测精度,但MEP3和MEP2预测的液滴粒径分布曲线几乎重合,说明增加约束并不一定能显著增加模型的预测效果。通过对比MEM、MEP1、MEP2和MEP3的液滴粒径分布预测结果表明,采用单个约束的最大熵预测模型预测的液滴粒径分布的峰值会偏向直径较大的一侧。

为了进一步验证MEP2分布模型对不同类型喷嘴产生的液滴的粒径分布预测的适用性,将MEP2应用于文献[18,25-29]中不同类型喷嘴的液滴粒径分布的研究中,并与文献中给定的实验数据进行对比,如图6所示。其中文献[18]采用对撞式喷嘴,喷嘴压强为2.2 MPa,实验数据共计8组,如图6a所示;文献[25]采用的平面射流喷嘴,液体流速1 m/s,空气流速93 m/s,实验数据共计100组,如图6b所示;文献[26]采用斯普瑞喷嘴喷头(1/4 TTG 0.3),喷雾流率3.52 mL/s,实验数据共计12组,如图6c所示;文献[27]采用旋流式气泡雾化喷嘴,喷嘴压强为0.5 MPa,实验数据共计24组,如图6d 所示;文献[28]采用压力旋流喷嘴,喷嘴流率0.16 m3/h,实验数据共计8组,如图6e所示;文献[29]采用静电喷雾方法,喷嘴流率为25 mL/min,高压发生器控制环形电极施加电压,实验数据共计22组,如图6f所示。

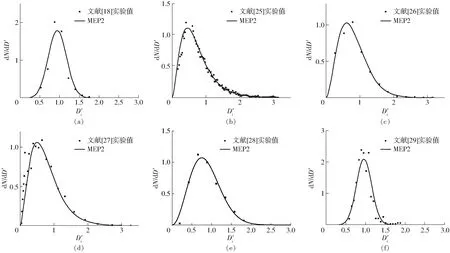
图6 MEP2模型对不同类型喷嘴的预测结果及实验数据对比

图7为MEP2对不同类型喷嘴产生的液滴的粒径分布计算结果的相关系数和均方根误差。从图7可以看出,MEP2分布预测的结果与实验数据较为吻合,相关系数都在0.9以上,均方根误差低于0.25,MEP2分布模型总体上能够反映不同类型喷嘴产生的液滴粒径的分布特性。同时也可以看出MEP2分布模型对于文献[25-26,28]计算的结果更好,相关系数都超过0.98,均方根误差均低于0.072,而对其他3篇文献计算的结果稍差。这是因为文献[25-26,28]采用的是比较简单的喷雾雾化工况,而文献[18,27,29]的雾化工况更加复杂。

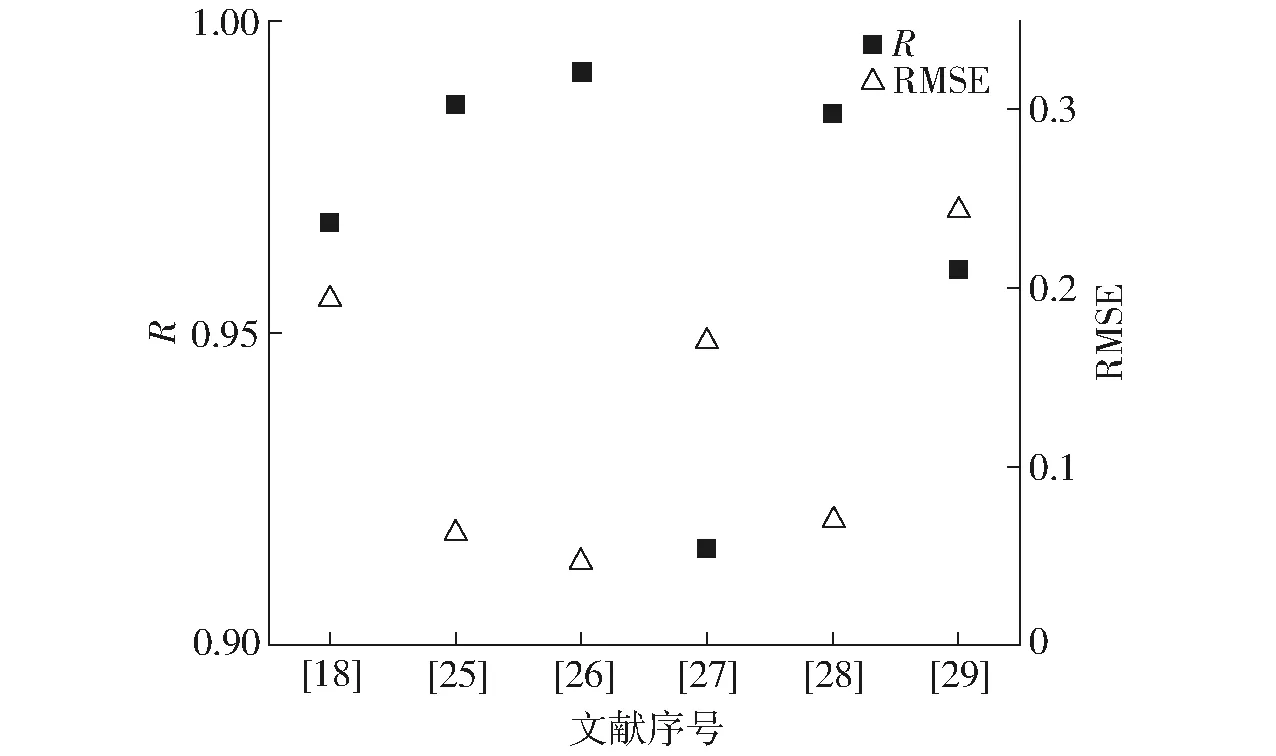
图7 MEP2模型对不同类型喷嘴的预测结果与实验数据的相关系数和均方根误差

3 预测模型应用

3.1 实验数据及参数

将MEP2预测模型应用于文献[22]中Pratt &Whitney Canada(PWC)公司制造的压力喷嘴的雾滴粒径分布的预测研究。实验参数如表5所示。

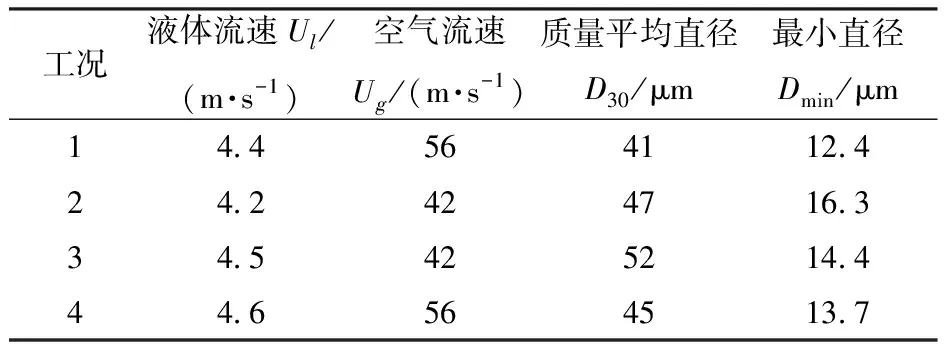
表5 不同工况条件下PWC压力喷嘴实验参数

3.2 基于无实验数据的平均直径计算

对预测模型的求解采用无实验数据情况的求解方法。MEP2分布预测模型中含有3个参数,所以式(17)中只需要D′10、D′20、D′30其中2个即可。又因为无量纲平均直径D′30=1,所以只需要在D′10、D′20中确定一个量就可以对预测模型方程组进行求解。D′10、D′20的计算可以利用式(28)求得。理论上选择D′10、D′20都不会影响预测结果,但通过式(25)～(28)求解平均直径时会产生误差,所以D′10、D′20的计算精确度直接会影响预测结果。为了尽量消除这个误差,本文应用表2中的统计数据,对已知D30的情况,通过式(25)求解D10、D20的准确性进行评估,计算结果如表6所示。

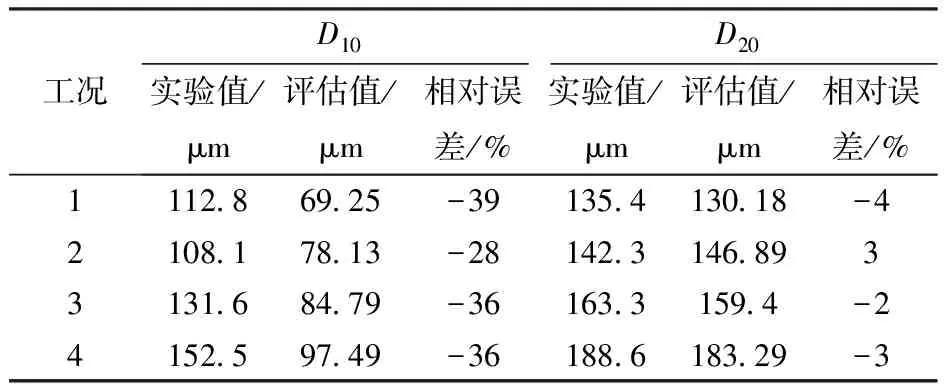
表6 平均直径D10、D20评估误差分析

从表6可以看出,D20的计算误差明显低于D10,所以本文选择D′20求解粒径分布函数。通过式(28)求得D′20=0.65。由于本文重点研究预测模型的可靠性,故为了过程简便,本文省略通过经验公式计算平均直径的步骤,直接用实验得到的平均直径D30和最小直径Dmin参与模型预测计算。

3.3 预测结果

研究表明,压水式喷嘴的最小直径往往不是从零值开始的[30],如图8所示。所以本文将通过D30无量纲化的最小直径D′0引入分布预测模型中,得分布模型为

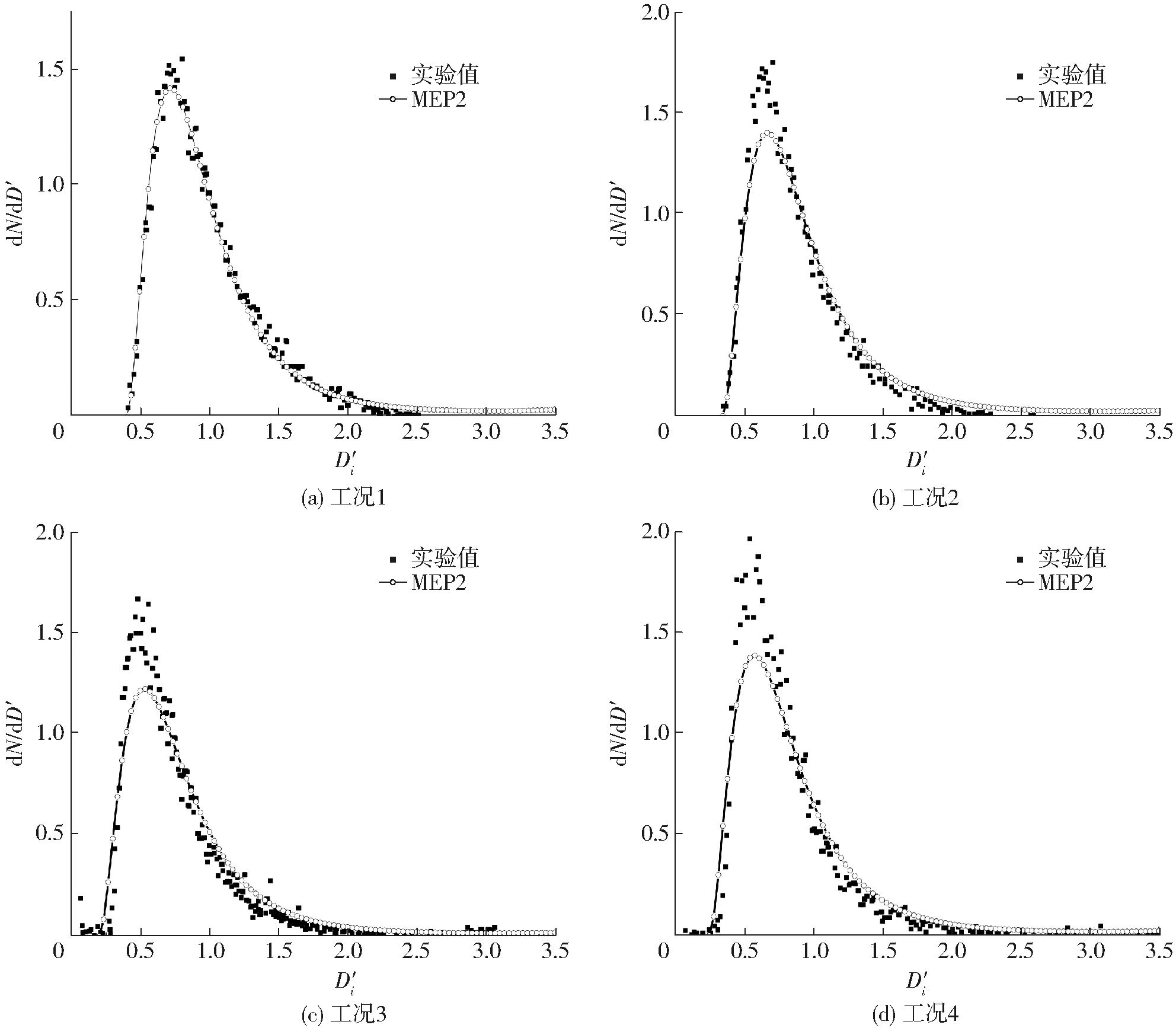
图8 PWC喷嘴实验与预测液滴粒径数量概率密度分布对比

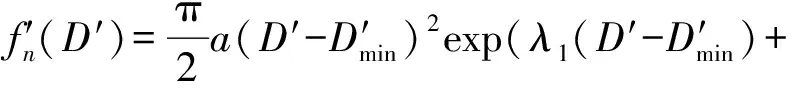
λ2(D′-D′min)2)

(31)

通过求解式(31)来确定分布参数a、λ1、λ2。积分上下限取D′min=D′0,D′max=3.5。求解的方程组为

(32)

从图8可以看出,模型预测的液滴粒径分布与实验数据基本一致。工况1条件计算结果的相关系数为0.994,均方根误差为0.072。PWC喷嘴在工况2、3、4情况下,模型预测液滴粒径数量概率密度分布的峰值较实验值低,相关系数分别为0.992、0.981、0.973,均方根误差分别为0.088、0.135、0.147。可以看出模型对于工况3和工况4预测的结果较差,这是因为应用式(28)对无量纲平均直径D′r0r求解过程中,在不同工况条件下存在一定的偏差导致。假如平均直径的计算足够准确,模型总体上能够反映不同工况条件下雾滴的粒径分布特征。

4 结论

(1)建立了雾滴粒径分布的最大熵模型,并通过数值方法求解闭合方程组的方法,确定液滴粒径分布函数,液滴粒径分布函数可以求出各种雾滴粒径范围所占的百分比,并且能够运用液滴数量分布函数对Dv0.1、Dv0.5、Dv0.9等喷头喷雾评价指标进行求解。

(2)应用环形鼓风喷嘴雾化的实验数据对液滴粒径分布模型进行优选。结果表明,本文构建的MEP2与MEP3分布模型能很好地适用于喷雾液滴的粒径分布预测。预测的液滴粒径分布与实验值的相关系数均高于0.96,均方差误差均低于0.135,并且预测的结果优于LN和MEM分布模型。通过对比MEP2和MEP3分布模型的AIC,表明MEP2模型是一个更优模型。

(3)应用不同类型喷嘴的雾化液滴粒径分布实验数据对三参数最大熵模型的适用性进行检验,结果表明模型的预测结果基本符合不同类型喷嘴雾化雾滴的粒径分布特征。最后应用MEP2模型预测Pratt &Whitney Canada公司制造的压力喷嘴的液滴粒径分布,对比结果显示预测值与实验数据基本吻合。在不同类型喷嘴情况下,模型均能获得良好的预测结果,表明本文构建的MEP2模型具有较广泛的适用性。