原子物理守恒问题分类探析

葛太平

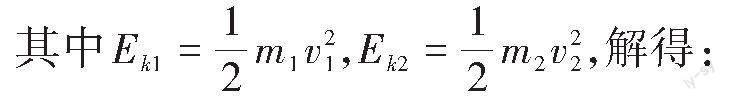
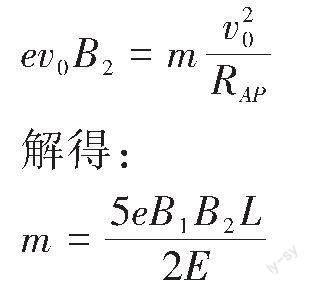
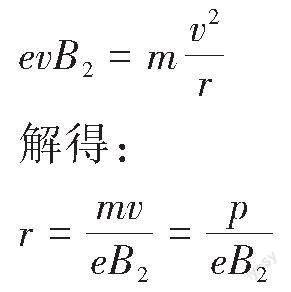
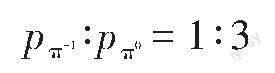
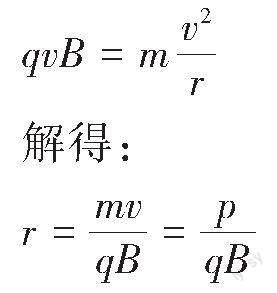
［摘 要］守恒问题是历年高考物理考查的重要问题，如力学中机械能守恒、动量守恒等。有关守恒问题，在历年高考中是常考常新的，值得重视。针对力学、电学中的守恒问题进行分析探讨的文章很多，这里就原子物理中的守恒问题进行分类探析。原子物理比较抽象，对初学原子物理的学生而言不易理解把握，学生解答相关问题时，稍不注意就容易丢分，但若能理解掌握好相应的规律，原子物理守恒问题又属于送分题。因此，广大高三教师和学生应当引起重视，确保这类题不丢分。高考原子物理试题中常考查的守恒规律有电荷守恒、质量数守恒、动量守恒、能量守恒，文章结合例题进行分类探析。

［关键词］守恒问题；原子物理；分类探析

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2023）17-0031-04

《普通高中物理课程标准（2017年版）》指出高中物理课程应进一步促进学生物理学科核心素养的养成和发展，其中物理学科核心素养最基本的素养为物理观念，物理观念是从物理学视角解释自然现象和解决实际问题的基础。在学生深度理解物理概念、规律的前提下，教师有必要引导学生分析物理现象，提炼概括物理本质，从物理学视角建立相对完整的图景，形成运用物理知识发现问题、解决问题的能力，从而有效提升学生的物理学科核心素养。

物理学中的守恒现象是指在一定的条件下，某些物理量守恒不变的物理现象，守恒观念对探索物理规律、解决物理问题起着重要作用。在原子物理考题中常渗透各种“守恒观”，如电荷守恒、质量数守恒、动量守恒、能量守恒等。原则上讲，一个或多个原子在一定的条件下，生成新的原子核，就发生了核反应；如果没有新核产生，但有能量变化，通常就会发生能级跃迁。从历年高考物理的考查情况来看，如果考题只考查电荷或质量数守恒，往往以核反应方程式书写的方式呈现，考题相对简单一些；如果考题要考查动量或能量守恒，则难度较大，往往涉及重核衰变或轻核聚变，其中的数学运算也相对较难。

为了分析讨论方便，本文结合教材及学生的学习实际，将核能利用中的重核衰变与轻核聚变中的动量守恒和能量守恒单列出来讨论，这样原子物理中的守恒大致可以分为：（1）能级跃迁中的守恒；（2）核反应中（不包括重核裂变、轻核聚变）的电荷、质量数守恒；（3）重核衰变与轻核聚变中的动量、能量守恒；（4）高能粒子变化中的守恒。下面结合典型物理题进行分析探讨，以期引导学生由浅入深地理解相关守恒规律的内涵，逐步、牢固树立守恒观念。

一、能级跃迁中的守恒

能级跃迁过程遵守能量守恒，在能级跃迁的过程中会有能量的释放或吸收，会产生相应的谱线。通常是原子的核外电子从较高的能级跃迁到相对稳定的能级，同时释放相应的能量，释放的能量应该与辐射的射线或光子的能量相等；同样，也可能是原子从外界吸收相应的能量，进而跃迁到较高的能级，而这两个不同能级间的能量差与吸收的射线或光子的能量相等。

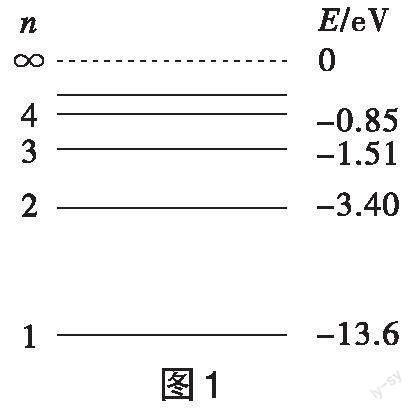
［例1］（2023年湖北省普通高中物理学业水平选择性考试第1题） 2022年10月，我国自主研发的“夸父一号”太阳探测卫星成功发射。该卫星搭载的莱曼阿尔法太阳望远镜可用于探测波长为[121.6 nm]的氢原子谱线（对应的光子能量为[10.2 eV]）。根据如图1所示的氢原子能级图，可知此谱线来源于太阳中氢原子（ ）。

A. [n=2]和[n=1]能级之间的跃迁

B. [n=3]和[n=1]能级之间的跃迁

C. [n=3]和[n=2]能级之间的跃迁

D. [n=4]和[n=2]能级之间的跃迁

分析：由于莱曼阿尔法太阳望远镜可用于探测波长为[121.6 nm]的氢原子谱线（对应的光子能量为[10.2 eV]），而从可探测的氢原子谱线对应的光子能量为[10.2 eV]可知，只有从[E2-E1=10.2 eV]，所以正确选项为A。

点评：能级跃迁题，基本上属于送分题，考生碰到这样的题目，不应该大意丢分。

二、核反应中的电荷、质量数守恒

在核反应过程中遵循最基本的电荷、质量数守恒这两个规律。这是书写核反应方程和判定核反应是否正确的依据。

［例2］（2023年高考物理全国甲卷第15题） 在下列两个核反应方程X + 147   N → Y + 178   O，Y + 73   Li → 2X中，X和Y代表两种不同的原子核，以Z和A分别表示X的电荷数和质量数，则（ ）。

A. [Z=1]，[A=1]         B. [Z=1]，[A=2]

C. [Z=2]，[A=3]         D. [Z=2]， [A=4]

解析：本题着重考查核反应方程中的电荷守恒及质量数守恒。可设原子核Y的电荷数和质量数分别为n和m，再写出两个核反应方程AZ   X + 147   N → mn   Y + 178   O， mn   Y + 73   Li → 2AZ   X。由核反应前后的质量总数不变、电荷守恒有[A+14=m+17]，[Z+7=n+8]；[m+7=2A]，[n+3=2Z]，聯立可求得[Z=2]，[A=4]。

［例3］现有 X、Y、Z三个原子核，其中X原子核放出一个正电子后变为原子核Y，原子核Y与质子发生核反应后生成原子核Z，同时放出一个氦原子核，请问下面说法正确的是（ ）。

A. 原子核X比原子核Z多一个质子

B. 原子核X比原子核Z少一个中子

C. 原子核X的质量数比原子核Z质量数大3

D. 原子核X与原子核Z的总电荷是原子核Y电荷的2倍

解析：设原子核X的电荷数为m，质量数为n，则核反应式为nm   X → +10  e + m-1n   Y，m-1n   Y + 11   H → 42   He + [n-3m-2]Z。原子核X比原子核Z多两个质子；原子核X的中子数为n-m，原子核Z的中子数为n-m-1，即原子核X比原子核Z多一个中子；原子核X的质量数比原子核Z的质量数大3；原子核X与原子核Z的总电荷数为2m-2，是原子核Y的电荷数的2倍。故C、D正确。

点评：这类题相对简单，考生只要依据核反应前后的电荷数和质量数守恒列方程，就可以解答。正确书写核反应方程是解决这类问题的关键，核反应一般是不可逆的，所以用箭头表示反应过程，反应前后电荷数、质量数守恒。

三、重核衰变与轻核聚变中的动量、能量守恒

（一）动量守恒

动量守恒定律是自然界普遍成立的基本规律之一。不论是宏观领域还是微观领域，大到宇宙天体，小到微观粒子，不论相互作用的是什么性质的力，动量守恒定律都是适用的。

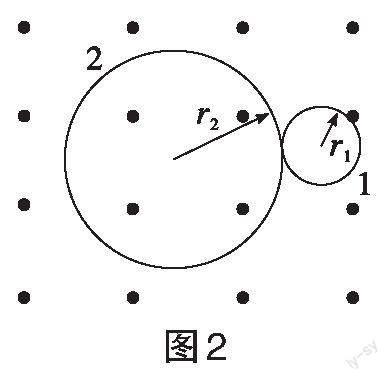
［例4］在匀强磁场中，一个原来静止的原子核，由于衰变放射出某种粒子，结果得到一张两个相切圆1和2的径迹照片如图2所示，已知两个相切圆的半径分别为[r1]、[r2]，则下列说法正确的是（ ）。

A.原子核可能发生[α]衰变，也可能发生[β]衰变

B.径迹2可能是衰变后新核的径迹

C.若衰变方程是[23892U→23490Th+42He]，则衰变后新核和射出粒子的动能之比为117∶2

D.若衰變方程是[23892U→23490Th+42He]，则[r1]∶[r2] = 1∶45

解析：原子核衰变过程中系统动量守恒，初态动量为零，衰变生成的两粒子动量方向相反，粒子速度方向相反，由左手定则知：若生成的两粒子电性相反，则在磁场中的轨迹为内切圆；若电性相同，则在磁场中的轨迹为外切圆，所以可能发生的是[α]衰变，不是[β]衰变，A错误；原子核衰变后生成的两核动量[p]大小相等、方向相反，粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：

由于p、B都相同，则粒子电荷量q越大，其轨道半径r越小，由于新核的电荷量大于[α]粒子的电荷量，则新核的轨道半径小于粒子的轨道半径，则径迹1为新核的运动轨迹，径迹2为[α]粒子的运动轨迹，故B错误。

点评：[α]、[β]衰变是原子物理中较为抽象的概念，可通过带电粒子在磁场中偏转这一直观的图景转化，进而揭开原子神秘的面纱，其本质是动量守恒在微观领域中的应用。

（二）能量守恒

能量守恒定律是自然界中最基本的规律之一，它是解决原子核问题的关键思想，常常和动量守恒定律一起运用。

［例5］云室处在磁感应强度为B的匀强磁场中，一静止的质量为[m1]的原子核在云室中发生一次[α]衰变，[α]粒子的质量为[m2]，电量为[q]，其运动轨迹在与磁场垂直的平面内。现测得[α]粒子运动的轨道半径[R]，试求在衰变过程中的质量亏损。（注：涉及动量问题时，亏损的质量可忽略不计）

［例6］已知氘核的质量为2.0136 u，中子的质量为1.0087 u，23   [He]核的质量为3.0150 u。两个速率相等的氘核对心碰撞聚变成[32He]核并放出一个中子，释放的核能全部转化为生成物的动能。若测得反应后生成中子的动能是3.12 MeV，则反应前每个氘核的动能是多少MeV？（质量亏损1 u时，释放的能量为931.5 MeV。除计算质量亏损外，23   [He]的质量可以认为是中子质量的3倍）

解析：由质量数与核电荷数守恒可知，核反应方程式为：21   H + 21   H → 23   [He] + 10   n

质量亏损为：

[Δm=2.0136×2u-（3.0150+1.0087）u=0.0035u]

释放的核能为：

[ΔE=Δmc2=931.5×0.0035 MeV=3.26 MeV]

设中子和氦核的质量分别为[m1]、[m2]，速率分别为[v1]、[v2]，反应前每个氘核的动能是[E0]，反应后中子和氦核的动能分别为[Ek1]、[Ek2]，核反应过程中系统动量守恒，以中子的速度方向为正方向，由动量守恒定律得：

[m1v1-m2v2=0]

由能量守恒定律得：

[2E0+ΔE=Ek1+Ek2]

[E0=0.45 MeV]

点评：原子核问题中的能量可以有静态的，也可以有动态的，但无论能量包含哪几种形式，总能量守恒。书写能量守恒方程时可以把质量亏损释放的核能[ΔE]拆分成反应物和生成物静态的能量形式即[Δmc2]，反应物的动能加反应物静态的能量等于生成物的动能加生成物静态的能量。这样对能量守恒有了更深层次的理解。

四、高能粒子变化中的守恒

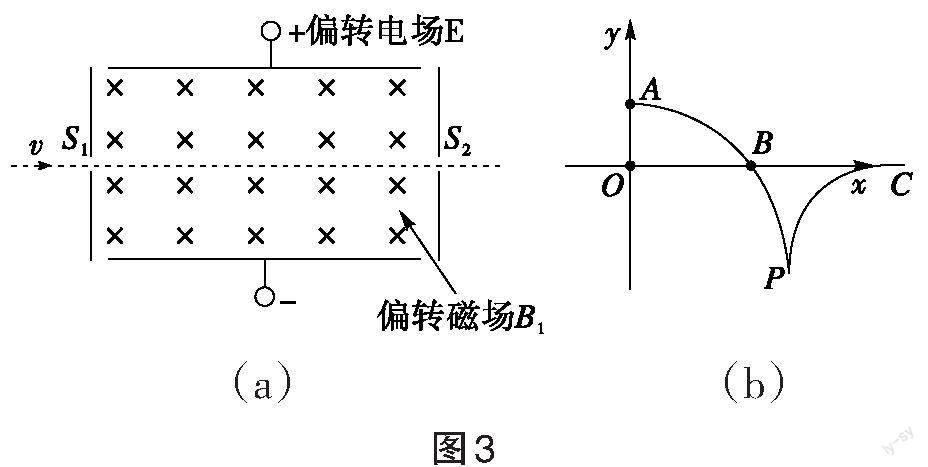
［例7］[k-1]介子的衰变方程为[k-1→π-1+π0]，其中[k-1]介子和[π-1]介子带负电，电荷量为元电荷电量e，[π0]介子不带电。现一[k-1]介子以某一初速度按图示沿直线穿过复合场区域Ⅰ［如图3（a）］，且该区域电场强度为E，方向竖直向下，磁场磁感应强度为[B1]，方向垂直纸面向里。穿过复合场Ⅰ后，k-1介子进入同一平面的[y]轴右侧单边界磁场区域Ⅱ，坐标轴与纸面平行，磁感应强度为[B2]，方向垂直于纸面。k-1介子在磁场区域Ⅱ中的运动轨迹如图3（b）所示，且OA的距离为L，OB的距离为2L，A、B为运动轨迹与坐标轴的交点。当[k-1]介子运动到P点时发生衰变，衰变后产生的[π-1]介子的轨迹是PC，两轨迹在[P]点相切（[π0]轨迹未画出），若两圆弧的半径[RAP]∶[RPC=2]∶1，不计微观粒子的重力，则：

（1）判断磁场区域Ⅱ的磁感应强度[B2]的方向；

（2）求k-1介子的初速度大小[v0]；

（3）求k-1介子的质量；

（4）求衰变后π-1介子与π0介子的动量比。

解析：（1）k-1介子带负电，由题意可知，k-1介子在磁场[B2]中向下偏转，應用左手定则判断磁场[B2]垂直纸面向里。

（2）k-1介子在复合场中做匀速直线运动，处于平衡状态，由平衡条件得：

[ev0B1=eE]

解得：

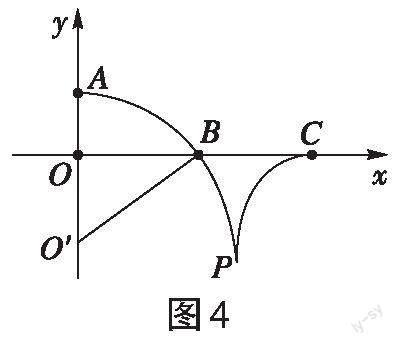
（3）k-1介子在磁场[B2]中做匀速圆周运动，运动轨迹如图4所示，由几何关系得：

[（RAP-L）2+（2L）2=R2AP]

解得：

[RAP=2.5L]

洛伦兹力提供向心力，由牛顿第二定律得

（4）带电粒子在磁场中做圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：

粒子动量：

[p=eB2r]

由题意可知：

由图示介子的运动轨迹可知，k-1与π-1的速度方向相反，以k-1初速度方向为正方向，介子衰变过程系统动量守恒，则

则

点评：本题考查了介子在磁场与电磁复合场中的运动，考查动量守恒定律的应用。介子在磁场中做圆周运动，在复合场中做匀速直线运动，分析清楚介子运动过程，求出介子做圆周运动的轨道半径，应用牛顿第二定律、平衡条件与动量守恒定律即可解题。

高中原子物理中的守恒问题将电荷守恒、质量数守恒、动量守恒、能量守恒这些自然界普遍成立的守恒定律体现得淋漓尽致，无不展现着物理学中的和谐美、简洁美和对称美。通过高中原子物理守恒问题的解决可有效培养学生的物理观念，提升学生的物理学科核心素养。

［   参   考   文   献   ］

［1］  中华人民共和国教育部.普通高中物理课程标准：2017年版［M］.北京：人民教育出版社，2018.

［2］  羊自力.对“物理观念”的初步理解及教学建议［J］.中学物理教学参考，2019（24）：6-7.

［3］  易继东.例析守恒定律在原子物理中的应用［J］.物理之友，2015（3）：39-40.