基于POF传感装置的混凝土裂缝开度预测

戚 丹, 包腾飞, 赵 珍

(1.杨凌职业技术学院 水利工程学院, 陕西 杨凌 712100; 2.河海大学 水利水电学院, 江苏 南京 210098)

1 前 言

内外环境的复杂性导致了水工混凝土结构中裂缝的产生具有不可预见性,裂缝扩展宽度是裂缝发展及坝体变形的重要参量,建立相应的裂缝开度预测模型,就能准确预测裂缝开度及其变化趋势,判断裂缝是否会发生失稳扩展,监控大坝结构是否安全。国外主要研究塑料光纤传感器如何监测建筑物应变、位移等,在裂缝监测方面涉足较少;国内主要研究混凝土坝裂缝定量监测及POF布设和开裂条件下塑料光纤的力光转换特性等[2-3],对基于POF传感装置的裂缝开展预测研究较少,本文将在以往研究不同光纤方位下光损耗值与裂缝开度的关系特性的基础上,尝试将不同光纤方位下光损耗值与裂缝开度关系进行量化,建立不同方位下裂缝开度预测模型,利用此预测模型由测量所得的光损耗值确定裂缝的扩展宽度,为后续进一步研究打下基础。

2 多项式回归预测模型

2.1 多项式回归分析

回归分析是一种传统的统计方法,建立在对有相互关系的客观事物大量试验和观察的基础上,用来寻找联系不确定的客观现象之间的统计规律,即处理变量x与y之间关系的一种统计方法和技术[4]。回归分析模型揭示事物间相关变量的数量关系,模型的建立涉及几个重要步骤,如图1所示。首先通过分析实际问题的目的设置因变量y,并选取影响y值的自变量x;其次进行这些变量数据的收集、整理,以便后期建立模型;然后寻找适当的数学形式来描述这些变量之间的关系(通过绘制散点图来选择数学模型,即将数据点绘制在坐标系中,根据这些点的分布状况最接近哪种曲线就用相应的函数来描述);最后,在回归模型建立之后,为了验证这个模型是否准确,进行回归模型的统计检验(包括拟合优度检验等)[5-6]。

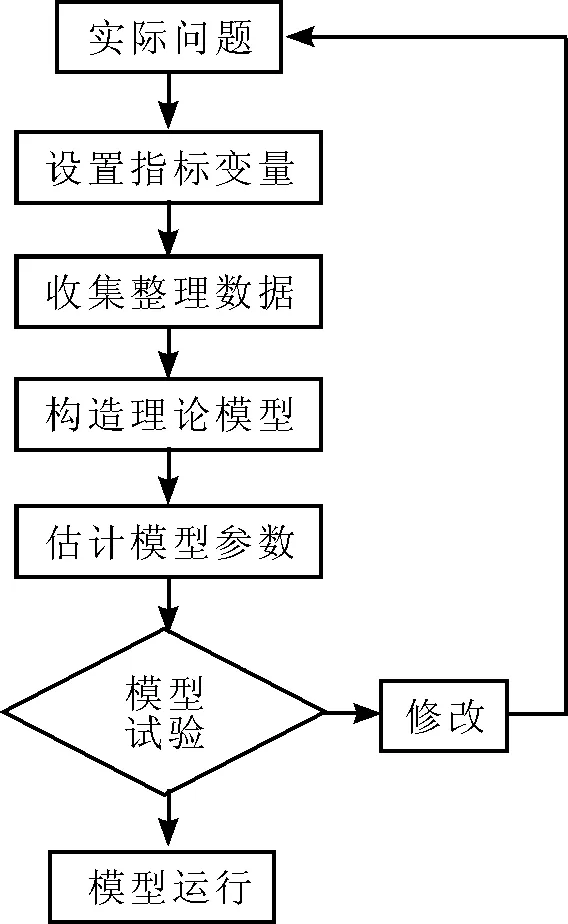
图1 回归模型建模步骤图

多项式回归分析是研究一个因变量与一个自变量或与多个自变量间的多项式关系的回归分析方法,包括一元多项式回归和多元多项式回归。举例如下:

一元n次多项式回归方程:

yi=ao+a1x+a2x2+…+anxn+εa

(1)

二元二次多项式回归方程:

(2)

式中:a0、b0为回归常数;εa、εb为随机误差;al、a2、…、an以及b1、b2、…、b12称为回归系数。

当两变量呈曲线关系时,需要用曲线方程式来拟合两个变量的数学关系,设其中的因变量为y,自变量为x,则两变量之间的关系可用式(2)来描述[7]。

2.2 裂缝开度预测模型

在已知不同光纤方位下裂缝开度与光损耗值对应数据的基础上,以这些数据作为样本,建立以光损耗值为自变量的裂缝开度预测模型。建立的裂缝开度预测模型涉及两个变量,分别为光损耗值和裂缝开度,从所研究问题的目的出发,设置裂缝开度为因变量,光损耗值为自变量。由以往的研究[8]可知光损耗值与裂缝开度关系呈曲线变化趋势,因此用式(2)来描述两变量之间的关系。

然而当所建模型中自变量的最高次数小于等于3时,回归系数容易解释,回归函数较稳定,回归模型的应用不会受到影响。因而,幂次超过3的模型不常使用[1],本文尝试建立二次多项式回归模型和三次多项式回归模型来预测裂缝开度,随后通过试验对比确定最优的多项式回归预测模型。

综上,建立二次多项式回归模型和三次多项式回归模型如式(3)、式(4)所示:

y=a0+a1x+a2x2

(3)

y=b0+b1x+b2x2+b3x3

(4)

式中:x为光损耗值;y为裂缝开度;a0、al、a2、a3以及b0、b1、b2、b3为回归系数。

3 实例分析

3.1 试验环节

由于塑料光纤传感器仅停留在试验研究阶段,还未用于实际工程的裂缝监测,本次试验将采用一种简单的塑料光纤(Plastic optical fiber,简称为POF)裂缝传感器装置展开。该简易POF裂缝传感器如图2所示,由三部分构成,分别为光源(功率为10 mW的红光笔,发射光波长为650 nm,与塑料光纤工作波长一致且对人体不造成伤害)、光强度传感介质(为三菱塑料光纤,包括与光源、光功率计连接的0.25 mm直径塑料光纤尾纤和测裂缝的塑料光纤裸纤)以及光强度测量设备(型号JW3233的光功率计)。

图2 塑料光纤裂缝传感器简易装置图

光源传输出来的光经过POF尾纤和POF裸纤后到达光功率计,POF裸纤因为外力作用发生弯曲变形时将出现光的外溢,使得到达光功率计的光的强度发生改变(变小)。图3为本次试验的裂缝模拟试验示意图。此时随着活动玻璃板移动距离越远(模拟建筑物裂缝扩展),光外溢越厉害,则光损耗越厉害。记录活动玻璃移动之前的光强度值,再记录活动玻璃移动时对应的光强度值,前者减去后者,可得到由于活动玻璃移动而产生的光强损耗值。重复以上工作便可通过POF裂缝传感器简易装置和裂缝模拟装置得到多组裂缝开度-光损耗值试验实测数据。

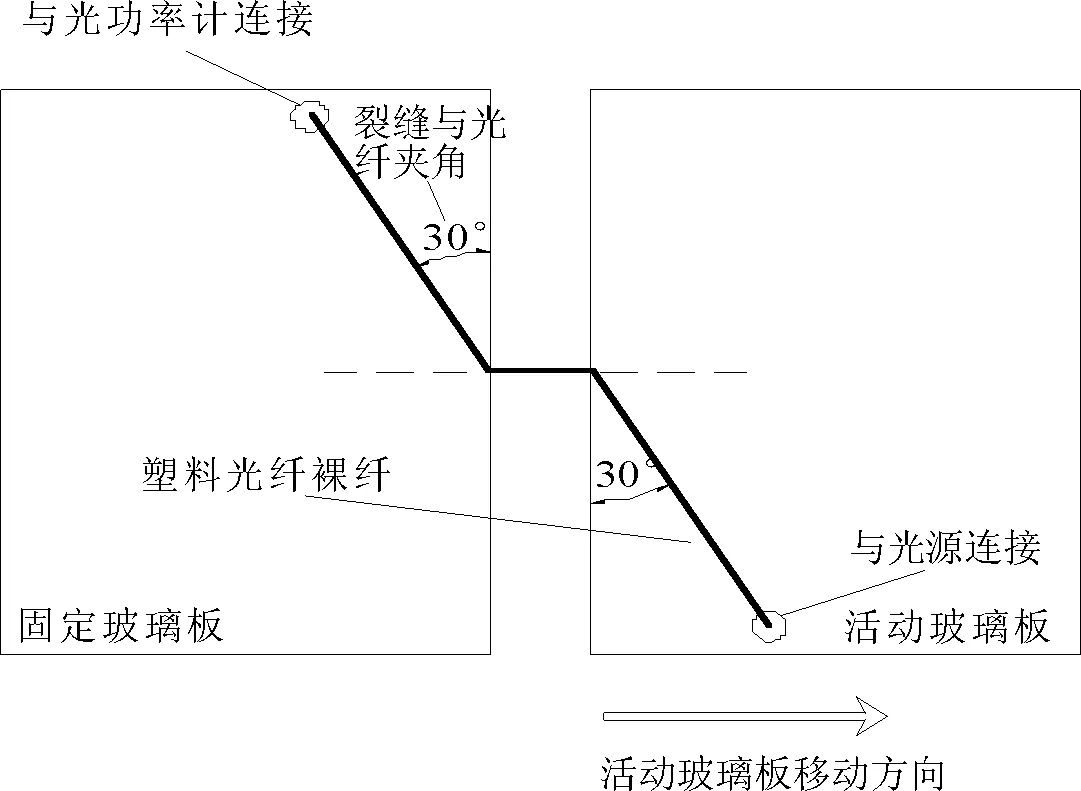
图3 裂缝模拟试验示意图

借助于试验设备,同时为了保证所建立模型的精度,增加试验实测数据的样本量,本次试验将采用精度为0.1 mm的游标卡尺来测量裂缝开度。最终通过多组试验,量测裂缝开度为0 mm、0.2 mm、0.4 mm、0.6 mm、……、5.8 mm、6 mm时的光损耗值,共计31组数据,如表1所示。其中,前21组数据用来建立预测模型,后10组数据用来验证模型精度。

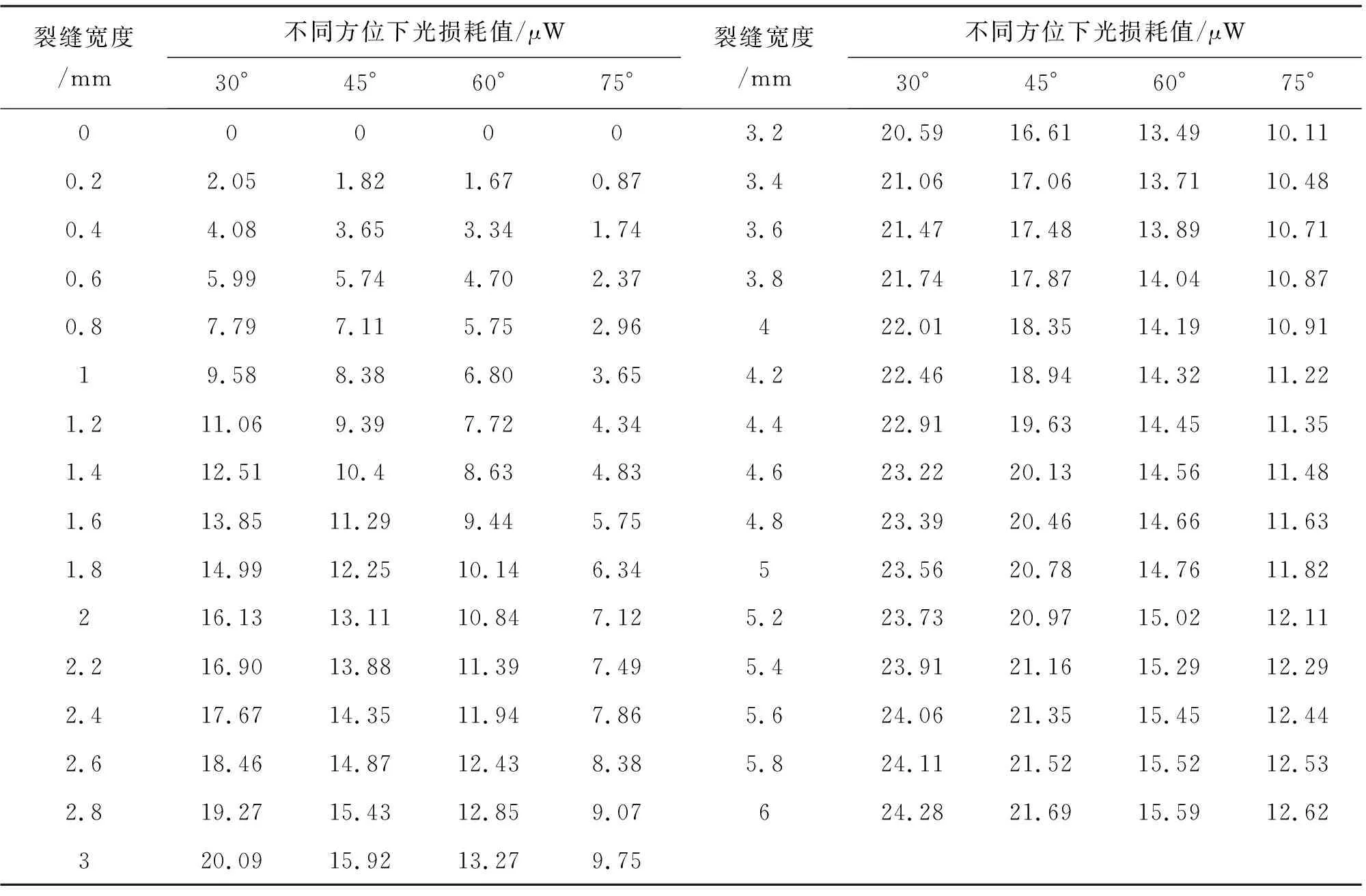
表1 试验实测数据表

3.2 预测模型建立

以表1前21组数据(即0 mm、0.2 mm、……、3.8 mm、4 mm缝宽及对应光损耗值)作为样本,结合式(3)和式(4),建立塑料光纤裂缝传感器在方位角30°、45°、60°、75°下的二次多项式裂缝开度预测模型和三次多项式裂缝开度预测模型,分别如式(5)～式(8)及式(9)～式(12)所示,其中裂缝开度为因变量(单位:mm),光损耗值为自变量(单位:μW)。

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

实测裂缝开度-光损耗值关系曲线及二次多项式模型曲线和三次多项式模型曲线如图4、图5所示。

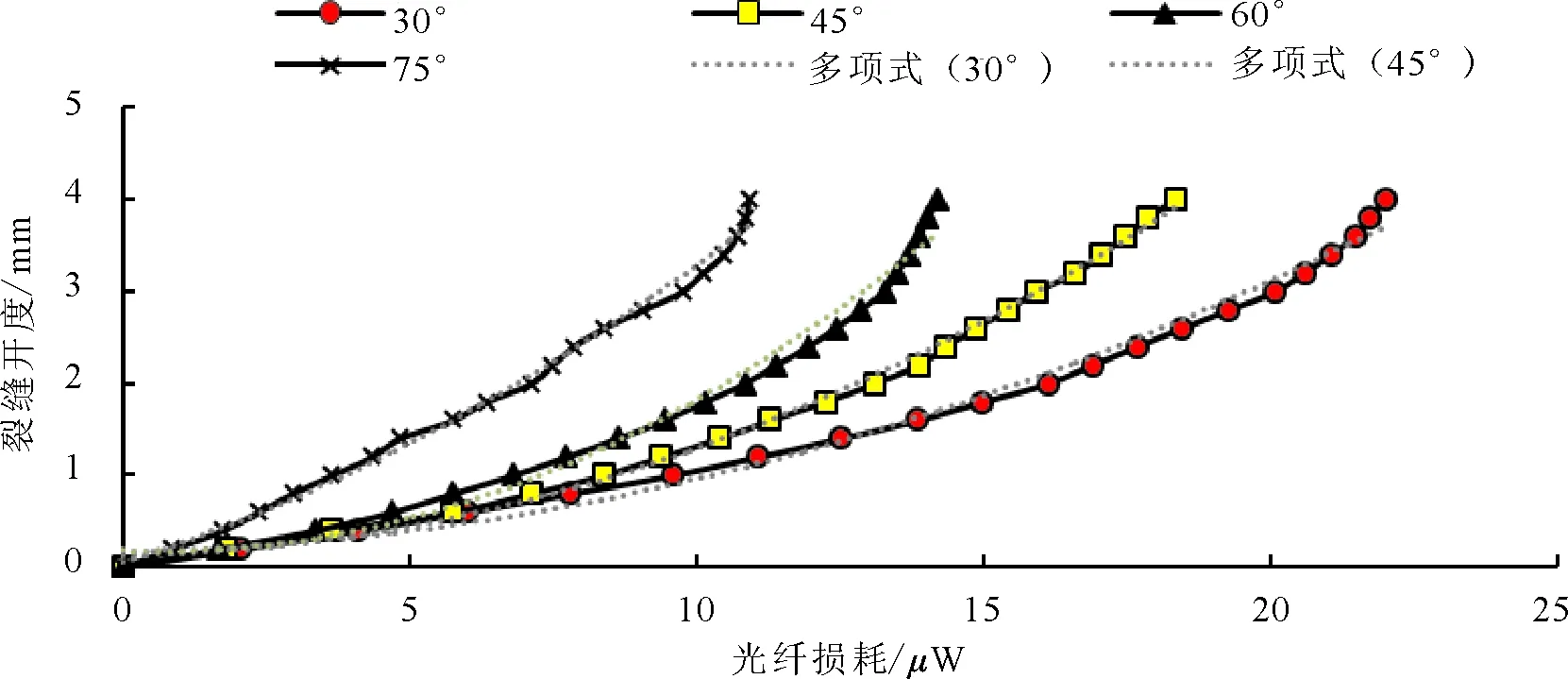
图4 不同方位角下裂缝开度-光损耗值实测曲线及二次多项式预测曲线

图5 不同方位角下裂缝开度-光损耗值实测曲线及三次多项式预测曲线

所得的不同方位下的二次多项式预测模型回归系数及样本决定系数见表2,三次多项式预测模型相关参数见表3。

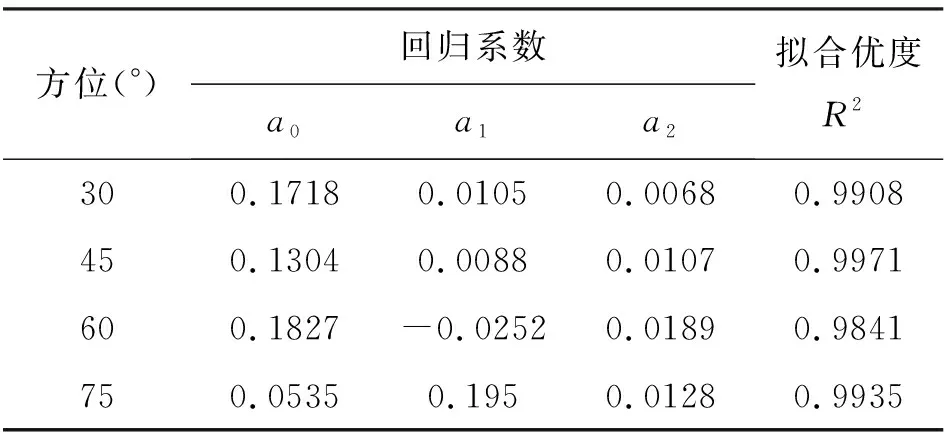
表2 不同方位下二次多项式回归模型参数表

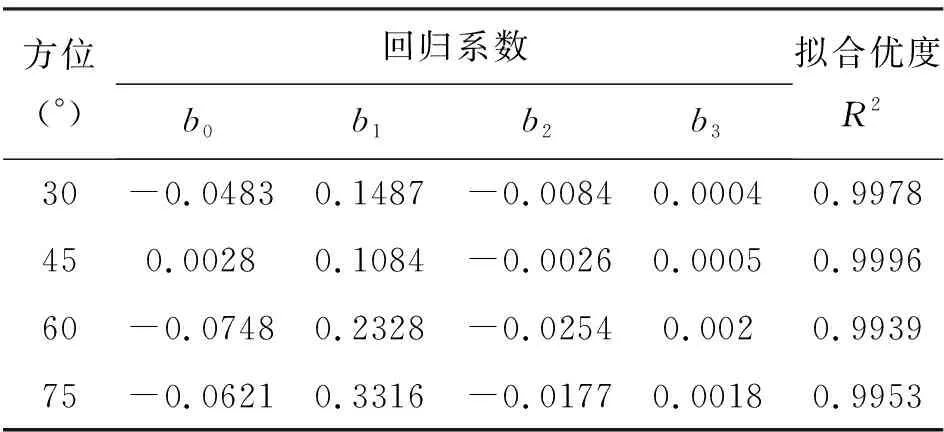
表3 不同方位下三次多项式回归模型参数表

表中R2为拟合优度,又称样本决定系数,表示预测值与实测值拟合优度的相对指标。R2取值介于0到1之间,R2越小,拟合优度越差,反之,拟合优度越好。八个回归模型的拟合优度R2全部大于0.984,且四个三次多项式回归模型的拟合优度超过了0.993,可见所建的二次多项式回归模型和三次多项式回归模型均较成功,且三次多项式的拟合精度更高。

3.3 裂缝开度预测

参考表1,将不同方位下大于4 mm缝宽对应的光损耗值代入式(5)～式(12)中,可得裂缝开度预测值,如表4～表7所示。

表4 30°方位角下裂缝开度预测值与实测值对比分析表

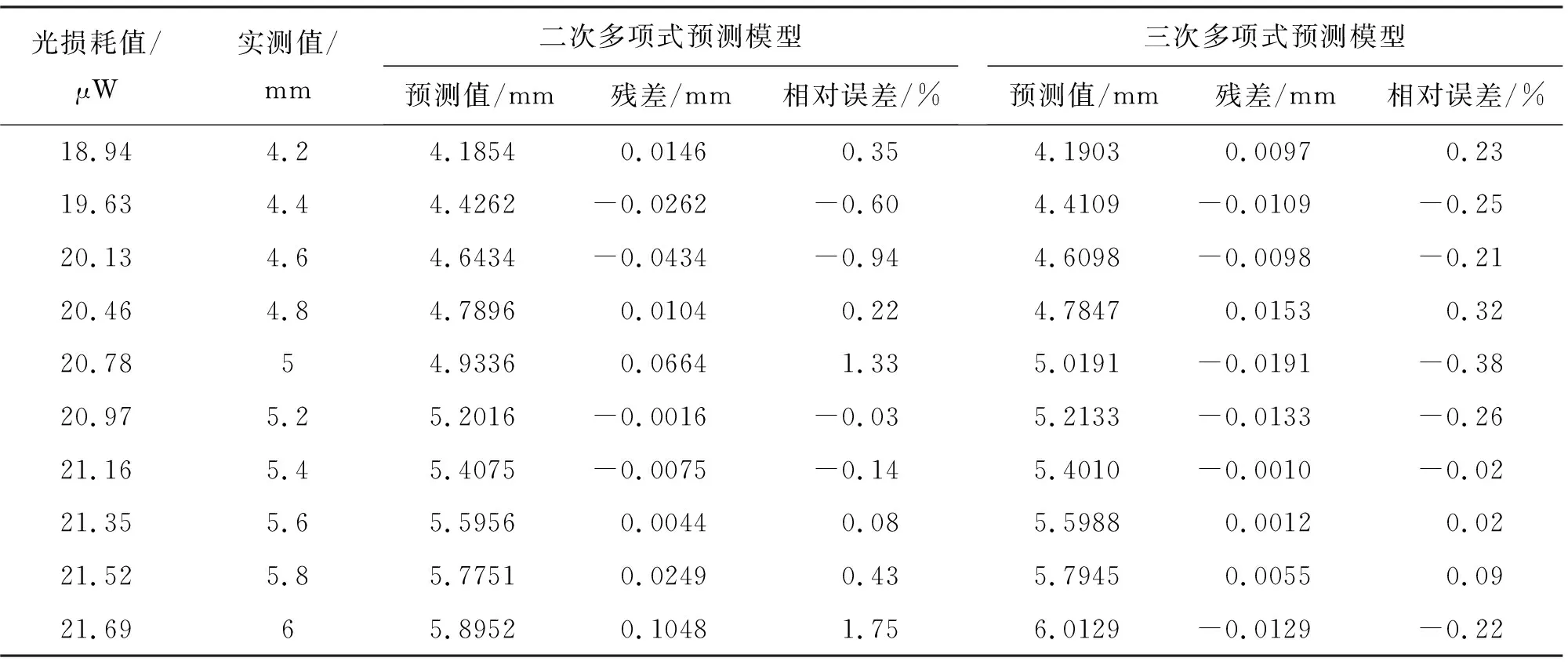
表5 45°方位角下裂缝开度预测值与实测值对比分析表

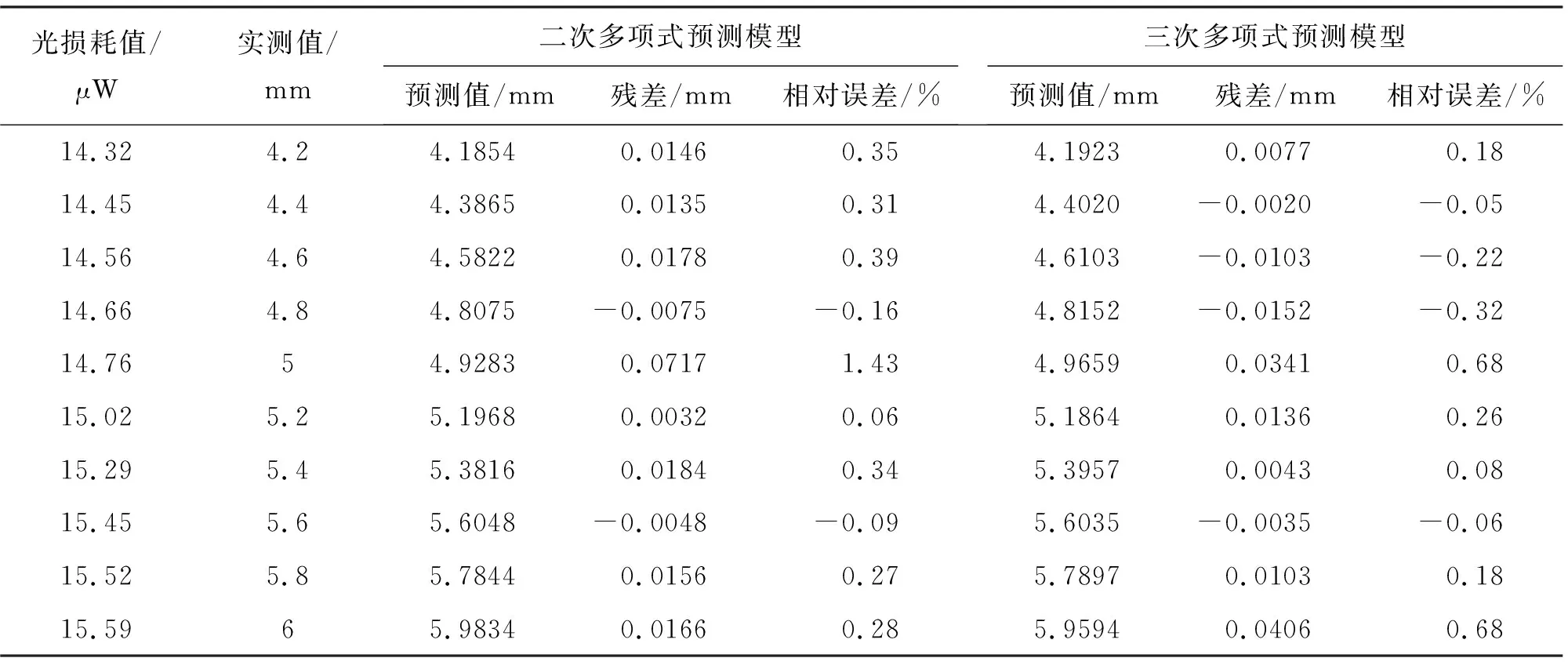
表6 60°方位角下裂缝开度预测值与实测值对比分析表

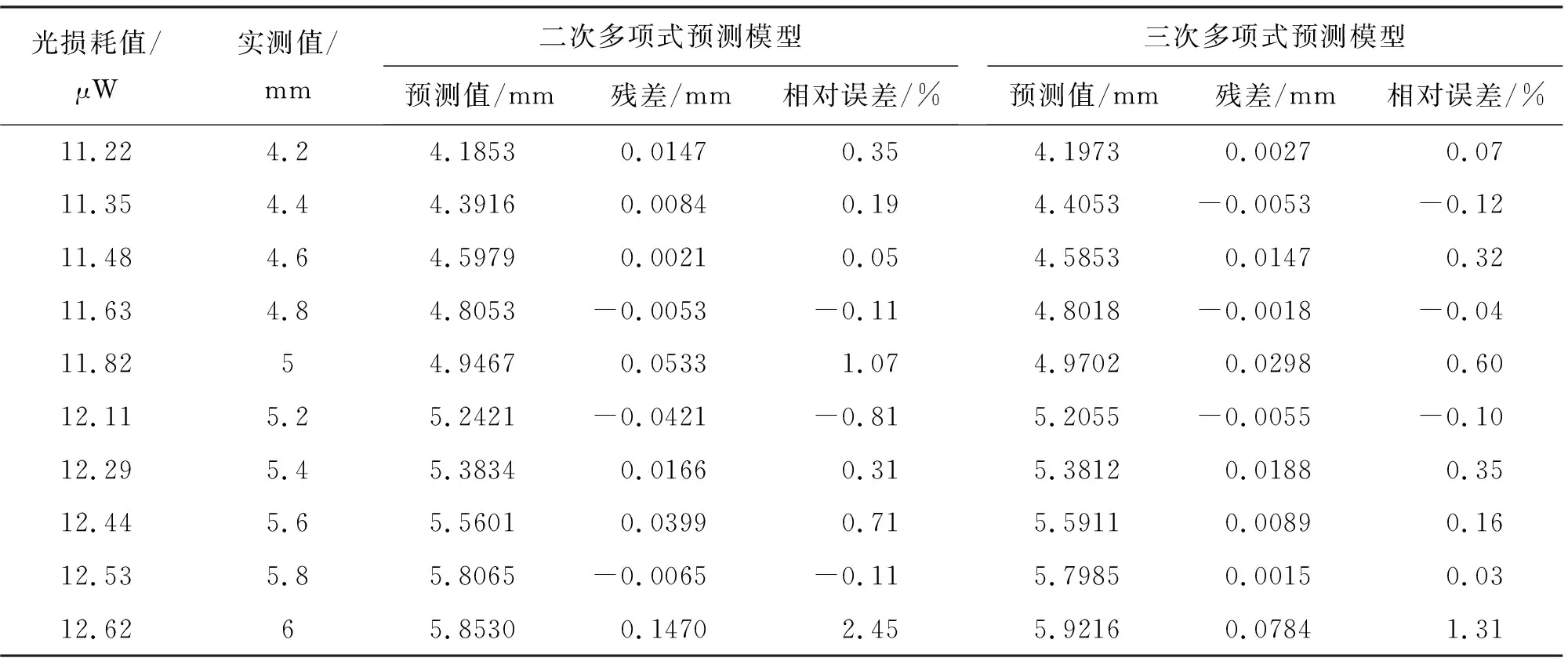
表7 75°方位角下裂缝开度预测值与实测值对比分析表

3.4 预测结果分析

由表4～表7可知,建立的八个裂缝开度预测模型的预测值相比于实测值,相对误差值基本小于1.0%,塑料光纤在30°、45°、60°、75°方位角下的二次多项式预测模型残差平方和分别为0.017、0.019、0.007、0.028,塑料光纤在30°、45°、60°、75°方位角下的三次多项式预测模型残差平方和分别为0.008、0.001、0.004、0.008,最大相对误差为0.92%,由此可知建立的八个预测模型均有较好的拟合精度,且三次多项式精度更高,这与3.2中的结论是一致的。

4 小结与展望

本文在介绍多项式回归基本理论知识的基础上,基于POF裂缝传感器建立了不同方位下二次和三次多项式回归裂缝开度预测模型,预测模型成功预测了裂缝的开展宽度,通过与实测数据的对比分析,验证了预测模型在预测裂缝开度方面的可行性,两种模型预测精度较高,且三次多项式模型精度更高。

但是,本文试验研究均是建立在模拟装置基础上,在实际工程中会遇到其他不可知的影响因素,因此所见模型的精度还需要结合实际工程进行进一步的研究和验证。