基于载流量降额因子的高压电力电缆热评估

2023-09-21袁燕岭邹红波朱振一

智慧电力 2023年9期

袁燕岭，高岭，邹红波，朱振一

（1.国网唐山供电公司，河北唐山 063000；2.三峡大学电气与新能源学院，湖北宜昌 4 430001；3.河北工业大学电气工程学院，天津 300130）

0 引言

电力电缆载流量是指电缆在不发生突然或逐渐退化的情况下的载流能力[1-3]。国际上根据电缆的正弦电流和100%负荷系数给出了标准容量表，但由于非线性负荷、开关仪表、电弧炉装置和瞬态电流等因素的影响，电力系统中很少出现正弦电流[4-5]。因此，在谐波电流中准确加载电缆或确定准确的载流量降额因子对避免电力电缆过热具有重要意义[6-7]。

国内外学者在对用解析法或有限元法计算电缆损耗[8-14]、载流量[15-19]和使用寿命[20-22]上已做了很多工作。在电缆损耗计算方面，文献[14]对光纤复合低压电缆内光纤温度与光纤传输损耗关系进行研究，通过分析仿真结果得到了优化其结构可有效降低电热效应对光纤本身的影响，但工作环境为低压，高压条件下电热效应会更加明显。文献[15]基于三芯铠装电缆的电磁-热耦合仿真模型研究了缆芯电流在低频输电方式下的不均匀分布特性，根据IEC 标准计算对比了铠装护套感应电压、损耗系数及电缆载流量的差异。在电缆载流量计算方面，文献[16-17]详细介绍了电缆载流量计算的基本原理以及日负荷曲线下电缆载流量计算的完整程序。文献[20]建立了10 kV 三芯交联聚乙烯电缆温度场和流场耦合仿真模型，研究了不同电缆敷设方式和直流拓扑结构对电缆直流载流量、温度分布和流场分布的影响规律，但其并未考虑谐波电流影响。在确定使用寿命方面，文献[21]对实际条件下考虑电压和循环负荷的高压电缆寿命进行了估算。在正弦电流下，在混凝土管道组中对地下电缆进行优化布置，改变输入参数以最大限度地延长电缆寿命[22]。忽略了谐波条件下的载流量计算和热分析。文献[23-24]虑及临近效应、集肤效应对电流密度分布的影响，推导了电缆在谐波下的电流密度分布解析表达式，引入修正因子以分析缆芯损耗、金属屏蔽层损耗、绝缘损耗，并通过仿真验证了计算方法的正确性。为了确定谐波电流条件下的降额因子，文献[25]使用基于Neher和McGrath 关系的技术来确定存在谐波电流时的电缆损耗。文献[26]引入对称配置低压电缆的降额因子，所有三相电缆的电缆损耗相等，但未考虑到日循环负荷对电缆谐波载流量和降额因子的影响。

本文提出了一种基于载流量降额因子的铠装高压电力电缆热评估方法，降额因子考虑了导体和金属铠装层的集肤效应和邻近效应，是通过电力电缆在不同谐波特征下的交直流电阻比定义的。采用有限元模拟计算了电缆在基波和谐波电流条件下的交直流电阻比，确定了稳态负荷条件下电缆降额系因子计算方法。根据国际电工委员会（International Electrotechnical Commission，IEC）标准进行了瞬态热分析以确定电缆温度和循环额定因数，基于Arrhenius 寿命模型和电缆故障率研究了电缆过载的可能性。结合不同截面积的高压电缆，通过计算日循环负荷和谐波电流下电缆载流量，对比验证了所提出方法的准确性。

1 稳态负荷条件下的热分析

1.1 谐波电流和稳态负荷下的载流量降额因子

谐波电流导致电缆容量比正弦条件下的减少，本文使用的高压电缆模型忽略其介质损耗，假定施加的电压恒定，因此介质损耗恒定。电缆损耗可以用交流与直流电阻之比来描述，该比值表示电缆在谐波条件下的变化率。在谐波电流存在的情况下，可以用有限元法计算电缆的电阻损耗。假设三相系统中谐波电流平衡，如式（1）所示：

式中：Ih为导体电流的各阶次谐波电流值；h为谐波阶次；t为时间；θ为相位差。

电缆p中的电缆总电阻损耗Ptot定义如式（2）所示：

式中：Rac,c,p(h)为电缆p在h次谐波下的交流电阻；λ1,h,p为电缆p在h次谐波下的铠装损耗因子；λ2,h,p为电缆p在h次谐波下的护套损耗因子；Id为电流有效值；αh为h次谐波电流值与电流有效值之比。

由于谐波电流损耗过大，电力电缆不能按正弦波额定电流加载，可能导致电缆寿命大幅降低。在以往的研究中，对于非铠装电缆，电缆降额因子的定义是:具有特定谐波特征的畸变电流的有效值与在电缆中产生相同损耗的基频电流的有效值之比。根据此定义，铠装电缆降额因子kd定义如式（3）所示：

式中：Rac,tot,p(h)为电缆p在h次谐波下的总电阻；Rdc为电缆直流电阻。

定义假定三相系统中电力电缆损耗相同，文献[19]考虑到多芯电缆中由于邻近效应，导体之间交流电阻差异较小，只考虑了导体的最大交流电阻。但在金属护套固体接地系统中，即使在相平衡电流下，环流电流损耗也不同。文献[20]定义的降额因子没有考虑到所需电缆中其他相邻电缆的影响，因此，式（3）的定义中考虑了金属护套损失。同时考虑相邻加载电缆的影响，提出了另一种新的降额因子Δθ，它被定义为使导体在畸变电流和不畸变电流下温升相等的总额定正弦电流的倍数，如式（4）所示：

式中：Δθh,p为电缆p在h次谐波下的温升。

假设电缆系统中最热的电缆为电缆q，考虑导体电流、护套电流、铠装电流以及相邻电缆引起的导体温升，利用交直流电阻比，并考虑导体、护套和铠装在电缆施工中为金属截面，降额因子kd,n的定义如式（5）所示：

式中：Rac,c,q(1) 为电缆q在1 次谐波下的交流电阻;T1，T2，T3，T4分别为绝缘热阻、护套与铠装的层间热阻、外护层热阻、电缆表面与周围介质间热阻；Rac,c,j为电缆j交流电阻;λ1,1,q为电缆q在基波下的铠装损耗因子；λ2,1,q为电缆q在基波下的护套损耗因子；λ1,1,j为电缆j在基波下的铠装损耗因子；λ2,1,j为电缆j在基波下的护套损耗因子；λ1,h,q为电缆q在h次谐波下的铠装损耗因子；λ2,h,q为电缆q在h次谐波下的护套损耗因子；λ1,h,j为电缆j在h次谐波下的铠装损耗因子；λ2,h,j为电缆j在h次谐波下的护套损耗因子；ρs为土壤热电阻率；dpj，d′pj分别为电缆q中心到电缆j中心的距离及其图像。

所研究的平层地下单导体电缆中，电力电缆的容量往往根据环流损耗较大的电缆来确定。然而，对于不清楚最热电缆的情况，对所有电缆进行计算，并选择最小值作为降额因子。

1.2 交直流电阻比计算

计算交直流电阻比的降额因子，必须确定铠装层的损耗系数。为了计算这些参数，采用有限元法计算了导体和电缆金属层的电阻损失，用这种方法可以在考虑导体和护套的集肤效应和邻近效应的情况下确定这些因素的准确值，在正弦频率和谐波频率下分别进行了有限元模拟，因此，谐波电流的总损耗是根据负荷电流的谐波阶数来确定的，有限元模型中各单元电流密度J根据涡流密度矢量Je和源电流密度矢量Js定义如式（6）所示：

式中：φ为电标量势；A为磁矢量势；▽为梯度算子；ρe为电阻率；ω=2πf，f为频率。

考虑Z 方向电流密度和二维问题的准稳态扩散方程式如式（7）所示：

式中：μ为材料的磁导率；x为横轴方向；y为横轴方向。

用有限元法求解计算各单元电流。因此，金属部件如导体和护套的电阻损失是根据每个元件中的电流计算的，用有限元模型将电缆各金属段的损耗、交直流电阻比和谐波频率联系起来，如式（8）所示：

式中：W为交流损耗；S为通流面积；Rac为交流电阻；Ys和Yp分别为集肤效应和邻近效应损耗系数。

2 日循环负荷下的热分析

2.1 谐波电流和日循环负荷下的载流量降额因子

考虑循环负荷系数，日循环负荷降额因子计算如式（9）所示：

式中：Kd为基于旧定义的降额因子；Kd,cyc为日循环负荷下的新降额因子；Kd,n为考虑相邻电缆热效应的降额因子；Kd,n,cyc为考虑相邻热效应的电缆在日循环负荷下的新降额因子；M为循环额定系数，可以通过热瞬态模拟计算得到。

2.2 电缆瞬态温度计算

热传导可以用模拟电流传导的方法来处理。阶梯网络的电缆层的构成可以通过一些热电阻和电容表示，以确定温度分布随时间的函数。根据IEC 60853 标准将梯形网络简化为两环路网络，将加载曲线划分为足够多的时间区间，从而得到时变载荷下的瞬态温升，因此假定载荷在任意时间区间为常数。周围土体作为热网第二回路的瞬态温升θe(t)如式（10）所示：

式中：Wt为时刻t焦耳损耗与介电损耗之和；Ei为指数积分；De为电缆外表面直径；L为电缆轴向埋深；δ为土壤扩散率。

相邻电缆的相互发热效应会降低电缆的载流能力，热计算中必须考虑到这种效应。因此，另一相邻电缆j导致电缆p的温升θpj(t)如式（11）所示：

式中：Wt,j为电缆j在时刻t的总焦耳损耗。

电缆p在时刻t的瞬态温升θp(t)如式（12）所示：

式中：θc(t)为时刻t的导体温升；θd(t)为电缆p中介质损耗引起的自身温升；α(t)为导体与电缆外表面之间瞬态温升的实现因子；θd,pj(t)为电缆j中介质损耗引起的电缆p温升。

考虑金属件电阻随温度变化θa(t)的Goldenberg方程如式（13）所示：

式中：θ(∞)为高于环境温度的导体稳态温升；ξ为0℃时温度系数的倒数；θ(0)为瞬态开始时导体温度的倒数；θ(t)为时刻t导体温度的倒数。

2.3 用IEC算法计算循环额定系数

IEC 标准考虑了在电缆导体中插入可变日负荷这个因素。循环额定系数M是指稳态额定电流乘以某1 d 周期内电流的允许峰值，使导体温度不超过额定温度的因数，定义如式（14）所示：

式中：μc为负荷损耗因子；τ为时刻数；θR(i)，θR(τ)分别为施加额定电流损耗的阶跃函数后第i时刻，第τ时刻导体的温升；θR(∞)为稳态温升；Yi为时刻i到i+1 的等效电流平方。

2.4 利用瞬态温度计算循环额定系数

依据日循环负荷利用瞬态温度确定考虑负荷电流变化的循环额定系数。该方法是根据瞬态温度计算电缆寿命的，然后选取寿命达到设计值的电缆电流值作为电缆容量。由于退化应力（如电气应力、热应力、机械应力和环境应力）的存在，电气元件的老化往往会导致失效，电缆故障可能由于电阻损失造成过热。一般电缆在用户的典型操作条件下，在每天相同的时间显示相同的电流值，因此电缆承受每日荷载循环。外加电压与时间近似恒定，机械应力和环境应力可以假设等于其设计值，相反，由于均方根电流的变化，在负荷周期的每段时间内，最高温度也会发生变化。给定dt时，恒定荷载下第i时刻电缆绝缘寿命损失dLFi如式（15）所示：

式中：L(E,M,θi(t))为最大电场、机械应力和瞬态温度恒定时的电缆寿命。

故障周期数q如式（16）所示：

式中：N为日加载周期的步数。

电缆的寿命时间是与失效成比例的循环次数。基于累积概率分布函数，可以计算电力电缆在任务时间tp内的失效概率P（L）和相关故障率h（L），进而计算得到日循环负荷加载下电缆的绝缘故障率：

式中：βt为累积概率分布函数的尺度参数；L63%为故障概率为63%的时间。

3 热分析和模拟结果

在本节中，根据谐波电流和日循环负荷对电缆降额因子进行了评估。利用有限元方法计算了不同谐波频率下的交直流电阻比，然后计算了谐波电流下稳态负荷的降额因子Kd，Kd，n，同时，通过热分析确定稳态负荷条件下的电缆载流量，以评估降额因子。在第2 节中，利用热评估的暂态温度来确定正弦电流和谐波电流条件下的电缆寿命、故障率和降额因子。

3.1 稳态负荷状态

第2 节所提方法适用于计算6/10 kV 高压电缆单导体的谐波降额因子。分别对120 mm2，240 mm2和630 mm23 个截面的电缆进行了研究，所有电缆采用铜芯、铅护套、交联聚乙烯绝缘、聚氯乙烯外包，电缆的铅护套两端均接地，因此，在正弦和谐波电流的所有热计算中都插入了循环电流损耗。电缆间距为每种电缆外径的2 倍，埋深1 m，土壤温度20℃，土壤电、热电阻率分别为100 Ωm，1.5 km/W。电缆的尺寸和50 Hz 基频正弦电流下的电缆容量如表1 所示。

表1 电力电缆参数Table 1 Power cable parameters

利用麦克斯韦二维稳态谐波介质对所研究的电力电缆进行了交直流电阻比的有限元模拟计算。在有限元模拟中考虑了集肤效应和邻近效应，因此，导体和金属护套中的不对称电流分布以及对电力电缆交直流电阻的影响可以准确地被考虑进去。有限元仿真中均认为电缆电流在不同谐波阶次下等于电缆额定正弦电流。电缆的交直流电阻比针对不同的谐波特征和高达19 阶的谐波进行计算，如图1 所示。由图1 可以看出，随着谐波阶数的增加，交直流电阻由于集肤效应和邻近效应的增加而增加，且电缆横截面越大，增量越大。由于护套接地系统，交直流电阻比在三次谐波中有很高的值。在这种情况下，护套的循环电流损耗高，导致比非三次谐波阶数更多的交直流电阻。值得注意的是，交直流电阻比是电缆的总电阻，并考虑了导体和护套损耗。

图1 不同电缆中的交直流电阻比Fig.1 AC to DC resistances ratios in different cables

在计算电缆降额因子时，考虑了3 种谐波曲线，将基于先前定义的降额因子和新的降额因子进行比较。在电力电缆系统中，所有横截面的电缆载流量都是使用屏障优化方法在谐波电流中确定的，表2 给出了稳态和100%负荷条件下的降额因子和载流量结果。

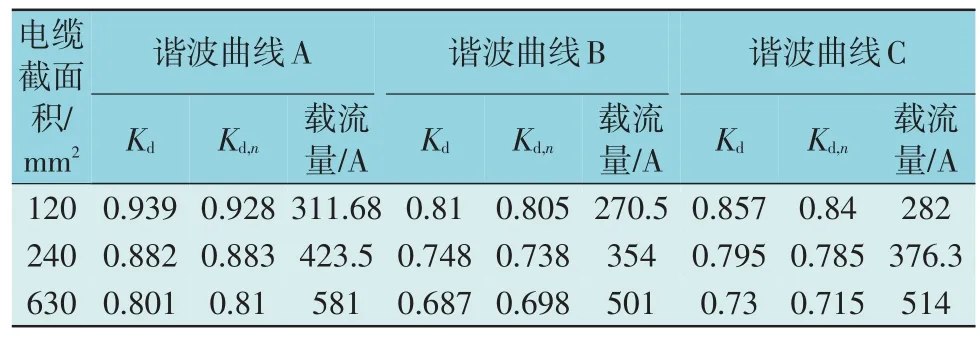
表2 稳态负荷条件下的电缆降额因子和载流量Table 2 Cable derating factor and ampacity under steady state load conditions

需要注意的是，降额谐波电流是用电缆额定正弦电流乘以Kd，n或Kd来计算的，这些值得到了失真电流的总均方根值，该电流可能不会降低电力电缆的设计寿命。所有电力电缆中的Kd，n都是针对地下扁平地层电缆中最热的电缆计算的。因此，降额因子与电缆载流量一致。对于截面积为120 mm2，240 mm2和630 mm2电缆，谐波曲线A 中新降额因子Kd，n与电缆载流量的差值分别为0.04%，0.04%和0.02%。基于旧定义的谐波A 降额因子Kd与电缆载流量的差值分别为1.14%，2%和1.1%，Kd，n的误差更小。因此，Kd误差不大，但准确值是根据Kd，n确定的。

3.2 日循环负荷

使用日循环负荷计算暂态温度和循环额定系数，日负荷曲线如图2 所示。在研究电缆规格和说明的程序下，120 mm2，240 mm2和630 mm2电缆使用IEC 方法的正弦电流循环额定因数分别为1.189，1.201 8 和1.224 5。

图2 日循环负荷Fig.2 Daily load cycle

根据图2 的负荷循环图计算正弦电流和谐波电流下电缆温度的日瞬态温度，根据日温度分布，可以估计出电缆的故障率和电缆过载的可能性。需要注意的是，在谐波电流分析中，日循环负荷每步（4 h）的谐波含量相对于基频是恒定的，即按日循环负荷图计算电流的基频，根据给定的谐波分布计算其他谐波阶数。所有电缆的设计寿命为30 a，最高允许温度为90℃，为了计算寿命和故障率，所有电缆的βt参数取为2。

图3 为正弦电流下截面积分别为120 mm2，240 mm2和630 mm2电缆的瞬态温度。需要注意的是，所有数据都是基于最大施加电流Im与额定电流IR的比值，仿真结果中的Im/IR与图2 日循环负荷的1 倍标称值有关，其他步的负荷值是根据每步的单位负荷电流和Im/IR值计算的。

图3 正弦电流下的电流瞬时温度Fig.3 Transient temperature under sinusoidal current

由图3 可知，电缆的最大负荷在日循环的第3步，而在第5 步结束时，所有电缆均达到日最高温度。研究结果表明，在日循环负荷中，最大负荷电缆的最高温度并不总是最高的，其随着电缆施工和日循环曲线的变化而变化。因此，有些情况下电缆最高温度没有达到最高允许温度或者在有限的时间内大于最高允许温度，而使用寿命也不会低于设计寿命。

正弦电流下各截面电缆寿命及故障率如图4所示，使用寿命为实线，故障率为虚线，且基于对数值显示，以获得更清晰的视觉效果。在图4 中，设计寿命用实虚线表示，虽然电缆截面越小，最高温度越高，但电缆的使用寿命越长，故障率越小。这是由于电缆结构使得时间常数减小，电缆截面越小，其最大电流越高。另一方面，在较小的截面上，电缆温度的下降速度更快，因此在瞬态寿命计算中，电缆寿命的总和要高于较大的截面。

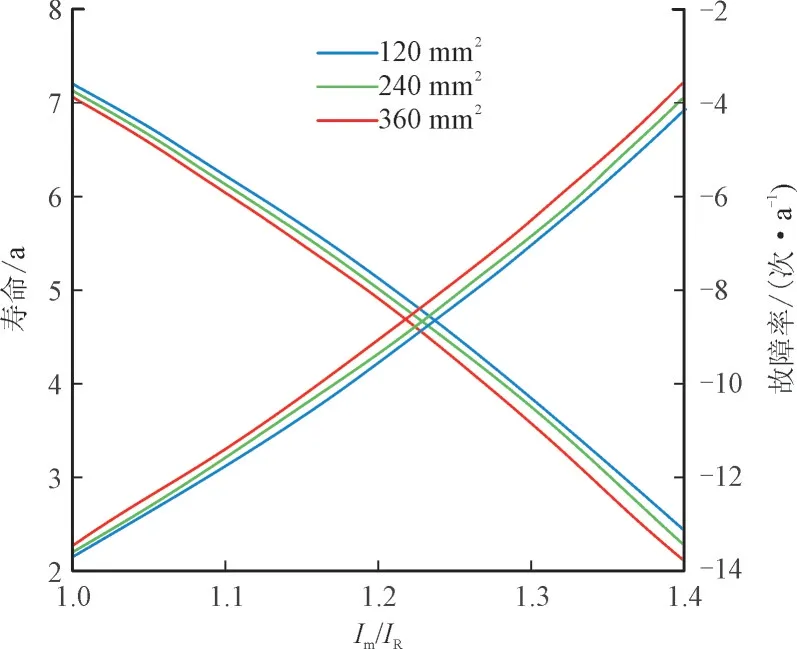
图4 正弦电流下各截面电缆寿命及故障率Fig.4 Cable life and failure rate of each section under sinusoidal current

在Im/IR=1 和日循环负荷的情况下，电缆的最高温度未达到额定温度。因此，要计算出准确的最大容量，必须考虑循环负荷系数。电缆达到最大允许温度的Im/IR值等于用IEC 方法计算的循环额定系数，但由于最高温度持续时间有限，电缆的使用寿命大于设计值。仿真结果表明，在正弦电流条件下，电力电缆可以在不降低设计寿命的情况下过载。

针对截面积为120 mm2，240 mm2和630 mm2电缆中不同过载值的电缆瞬态温度，分别计算了A，B，C 这3 种谐波剖面的寿命和故障率，如图5 所示。在谐波曲线中，电缆截面较大时达到最高温度，与正弦电流相似，电缆在负荷循环的第5 步达到最高温度，由于谐波电流存在，电缆的最高温度要大大高于正弦条件的。由于电缆的三次谐波阶数和交直流电阻比的显著增加，类似Im/IR值的谐波曲线B 最高温度比A 高。谐波曲线B 和C 的使用寿命比谐波曲线A 的使用寿命要短，这是由于与接地系统相比，具有闭合路径的电缆的铅护套中的循环电流损耗很大。需要注意的是，由于三次谐波阶数较多，谐波曲线B 的使用寿命较低，故障率高于谐波曲线C，在这种情况下，寿命随电流的增加而减少的速率也逐渐变大。

图5 不同谐波曲线下的电缆瞬时温度Fig.5 Cables transient temperature under different harmonic curves

但在谐波电流分布中，载流量应降额，但考虑到日循环负荷，可增加最大允许载流量。根据IEC算法和瞬态温度，日循环负荷条件下Kd，n和Kd的降额因子分别列于表3 和表4，考虑日循环负荷时，降额因子乘以IEC 和瞬态温度计算的循环额定系数。此外，为了研究降额因子结果，根据安培和单位值（Im/IR）确定的谐波日循环负荷的载流量如表5所示。正弦电流中的单位值可以作为基于瞬态温度的循环额定值引入，正弦电流下120 mm2，240 mm2和630 mm2电缆的瞬态温度循环负荷因子分别为1.33，1.323 和1.313。通过与IEC 算法计算值的比较，可以看出IEC 算法低估了负荷循环因子，比较结果验证了新定义的谐波电流降额因子和暂态温度下的循环负荷系数的计算结果。

表3 基于IEC方法的日循环负荷电缆降额因子Table 3 Cable derating factor of daily duty cycle conditions based on IEC method

表4 基于瞬态温度的日循环负荷电缆降额因子Table 4 Cable derating factor of daily cycle load based on transient temperature

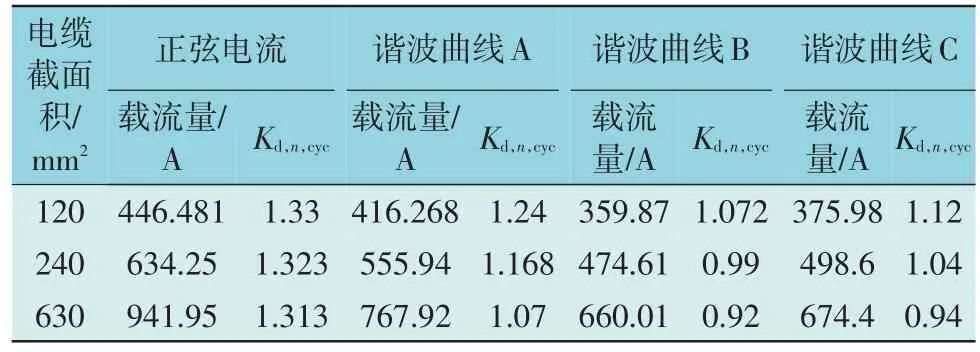
表5 日循环负荷条件下电缆载流量Table 5 Ampacity of cables in daily load cycle condition

在谐波曲线A 中，120 mm2，240 mm2和630 mm2的电缆使用表3 中Kd，n，cyc计算的载流量与表5 中计算的载流量之间的偏差分别为11%，9.2%和7.5%，120 mm2，240 mm2和630 mm2的电缆使用表4 中的Kd，n，cyc计算的载流量与表5 中计算的载流量之间的偏差分别为0.8%，0.02%和0.6%。在相似条件下，对120 mm2、240 mm2和630 mm2的电缆使用Kd，cyc计算的载流量在表5 中的偏差分别为9.96%，9.3%和8.4%，和0.8%，0.2%和1.9%，由此说明表4 中根据瞬态温度和降额因子的新定义确定的Kd，n，cyc的精度更高。表4 中基于瞬态温度的Kd，cyc得到的可接受值具有较低的误差，但表3 中使用Kd，cyc和Kd，n，cyc的载流量低估了电缆载流量，在其他谐波剖面中也观察到了类似的现象，因此，载荷循环因子可以与基于瞬态温度的Kd，n，cyc一起使用，以获得更精确的结果。